2022-2023学年沪教版(上海)数学七年级第一学期9.15十字相乘法 课件 (共14张PPT)
文档属性
| 名称 | 2022-2023学年沪教版(上海)数学七年级第一学期9.15十字相乘法 课件 (共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 177.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 09:23:52 | ||
图片预览






文档简介
(共14张PPT)
9.5.15十字相乘法
学习目标
通过复习整式的乘法与因式分解的互逆关系,理解十字相乘的概念,并掌握用十字相乘法来分解二次项系数为1的二次三项式;
培养学生的分析、综合及逆向思维能力,以及发现问题、探索规律的能力;
通过学生之间的交流与讨论,激发学生的求知欲,营造亲切、和谐、活泼的课堂气氛。
1、什么是因式分解?
2、我们现在学过哪几种因式分解的方法?
因式分解
的方法
提取公因式法
公式法
平方差公式
完全平方公式
3 、因式分解时,你认为应注意些什么?
计算 : (x+3) (x+1) =
(x+3) (x+1)=x2+4x+3
分解因式:x2+4x+3=
x2+4x+3= (x+3) (x+1)
x2 +4x+3 =
因式分解
3
4
x
x
+3
+1
x
+
3x
= 4x
(x+3)
(x+1)
十字相乘法
“竖分横写”
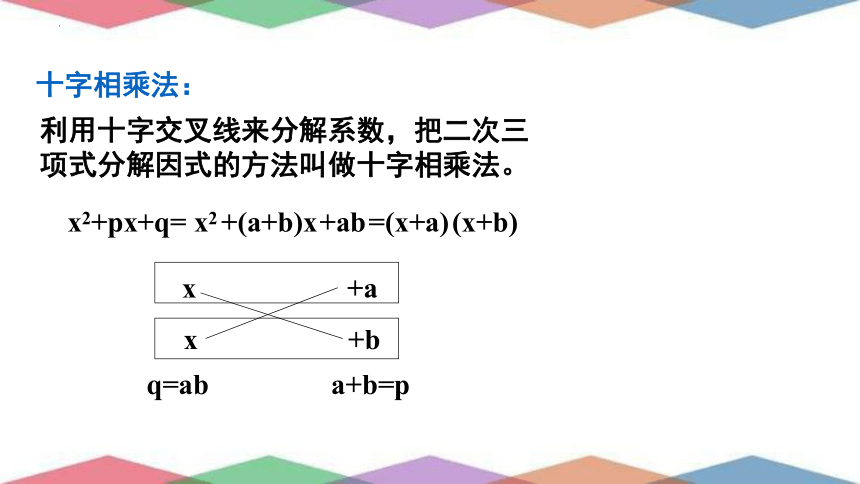
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法。
十字相乘法:
x2+px+q=
(x+b)
q=ab
=(x+a)
a+b=p
+ab
+(a+b)x
x2
x +a
x +b
分解因式:
(1)x2-7x+12; (2 )x2-4x-12;
(1) x2-7x+12 = (x - 3)(x - 4).
x +2
x +1
x -6
x +2
(2) x2-4x-12 = (x - 6)(x + 2).
分解因式:
(3)x2+8x+12; (4 )x2-11x-12.
(3) x2+8x+12 = (x +2)(x +6).
x +2
x +6
x -12
x +1
(2) x2-11x-12 = (x - 12)(x + 1).
对二次三项式x2 + px + q进行因式分解,应重点掌握以下三个方面:
1.掌握方法: 拆分常数项,验证一次项.
2.符号规律:
当q>0时,a、b同号,且a、b的符号与p的符号相同;
当q<0时,a、b异号,且绝对值较大的因数与p的符号相同.
3.书写格式:竖分横积
分解因式:
(1)x2+5xy-24 y2 ; (2 )x4-5x2-36; (3)(2x+y)2+6(2x+y)-27 .
(1)x2+5xy-24 y2
= (x +8y)(x -3y).
x +8y
x -3y
(2) x4-5x2-36
= (x 2+4)(x2 -9)
=(x 2+4) (x +3)(x -3).
x2 +4
x2 -9
(3) (2x+y)2+6(2x+y)-27
= (2x+y+9) (2x+y-3)
(2x+y) +9
(2x+y) -3
练一练:
小结:
用十字相乘法把形如
二次三项式分解因式
当q>0时,q分解的因数a、b( )
当q<0时, q分解的因数a、b( )
同号
异号
将下列各式分解因式
观察:p与a、b符号关系
小结:
当q>0时,q分解的因数a、b( )
同号
异号
当q<0时, q分解的因数a、b( )
且(a、b符号)与p符号相同
(其中绝对值较大的因数符号)与p符号相同
试将
分解因式
提示:当二次项系数为-1时 ,先提出负号再因式分解 。
1、十字相乘法
(借助十字交叉线分解因式的方法)
2、用十字相乘法把形如x2 + px +q 二次三项式分解因式
3、 x2+px+q=(x+a)(x+b) 其中q、p、a、b之间的符号关系
q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符号相同
当q<0时, q分解的因数a、b( 异号) (其中绝对值较大的因数符号)
与p符号相同
9.5.15十字相乘法
学习目标
通过复习整式的乘法与因式分解的互逆关系,理解十字相乘的概念,并掌握用十字相乘法来分解二次项系数为1的二次三项式;
培养学生的分析、综合及逆向思维能力,以及发现问题、探索规律的能力;
通过学生之间的交流与讨论,激发学生的求知欲,营造亲切、和谐、活泼的课堂气氛。
1、什么是因式分解?
2、我们现在学过哪几种因式分解的方法?
因式分解
的方法
提取公因式法
公式法
平方差公式
完全平方公式
3 、因式分解时,你认为应注意些什么?
计算 : (x+3) (x+1) =
(x+3) (x+1)=x2+4x+3
分解因式:x2+4x+3=
x2+4x+3= (x+3) (x+1)
x2 +4x+3 =
因式分解
3
4
x
x
+3
+1
x
+
3x
= 4x
(x+3)
(x+1)
十字相乘法
“竖分横写”
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法。
十字相乘法:
x2+px+q=
(x+b)
q=ab
=(x+a)
a+b=p
+ab
+(a+b)x
x2
x +a
x +b
分解因式:
(1)x2-7x+12; (2 )x2-4x-12;
(1) x2-7x+12 = (x - 3)(x - 4).
x +2
x +1
x -6
x +2
(2) x2-4x-12 = (x - 6)(x + 2).
分解因式:
(3)x2+8x+12; (4 )x2-11x-12.
(3) x2+8x+12 = (x +2)(x +6).
x +2
x +6
x -12
x +1
(2) x2-11x-12 = (x - 12)(x + 1).
对二次三项式x2 + px + q进行因式分解,应重点掌握以下三个方面:
1.掌握方法: 拆分常数项,验证一次项.
2.符号规律:
当q>0时,a、b同号,且a、b的符号与p的符号相同;
当q<0时,a、b异号,且绝对值较大的因数与p的符号相同.
3.书写格式:竖分横积
分解因式:
(1)x2+5xy-24 y2 ; (2 )x4-5x2-36; (3)(2x+y)2+6(2x+y)-27 .
(1)x2+5xy-24 y2
= (x +8y)(x -3y).
x +8y
x -3y
(2) x4-5x2-36
= (x 2+4)(x2 -9)
=(x 2+4) (x +3)(x -3).
x2 +4
x2 -9
(3) (2x+y)2+6(2x+y)-27
= (2x+y+9) (2x+y-3)
(2x+y) +9
(2x+y) -3
练一练:
小结:
用十字相乘法把形如
二次三项式分解因式
当q>0时,q分解的因数a、b( )
当q<0时, q分解的因数a、b( )
同号
异号
将下列各式分解因式
观察:p与a、b符号关系
小结:
当q>0时,q分解的因数a、b( )
同号
异号
当q<0时, q分解的因数a、b( )
且(a、b符号)与p符号相同
(其中绝对值较大的因数符号)与p符号相同
试将
分解因式
提示:当二次项系数为-1时 ,先提出负号再因式分解 。
1、十字相乘法
(借助十字交叉线分解因式的方法)
2、用十字相乘法把形如x2 + px +q 二次三项式分解因式
3、 x2+px+q=(x+a)(x+b) 其中q、p、a、b之间的符号关系
q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符号相同
当q<0时, q分解的因数a、b( 异号) (其中绝对值较大的因数符号)
与p符号相同
