数学人教A版(2019)选择性必修第一册3.2.2双曲线的简单几何性质 课件(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.2.2双曲线的简单几何性质 课件(共25张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 35.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-17 10:34:17 | ||
图片预览







文档简介
(共25张PPT)
3.2 双曲线
3.2.2 双曲线的简单几何性质1
《悲伤的双曲线》
如果我是双曲线,你就是那渐近线。
如果我是反比例函数,你就是那坐标轴。
虽然我们有缘,能够生在同一个平面。
然而我们又无缘,漫漫长路无交点。
为何看不见,等式成立要条件。
难到正如书上说的,无限接近不能达到。
如果我是双曲线,你就是那渐近线。
#复习回顾
双曲线:在平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线。
||PF1|-|PF2||=2a < 2c
(a>0,b>0,且c2=a2+b2)
双曲线的标准方程:
焦点在x轴:
焦点在y轴:
类比椭圆的简单几何性质,你认为应该研究双曲线的哪些几何性质?
问题探究
一、范围
F1
F2
O
由方程
≥ 1
则 x ≤ -a或x≥ ≤ a
y ∈ R
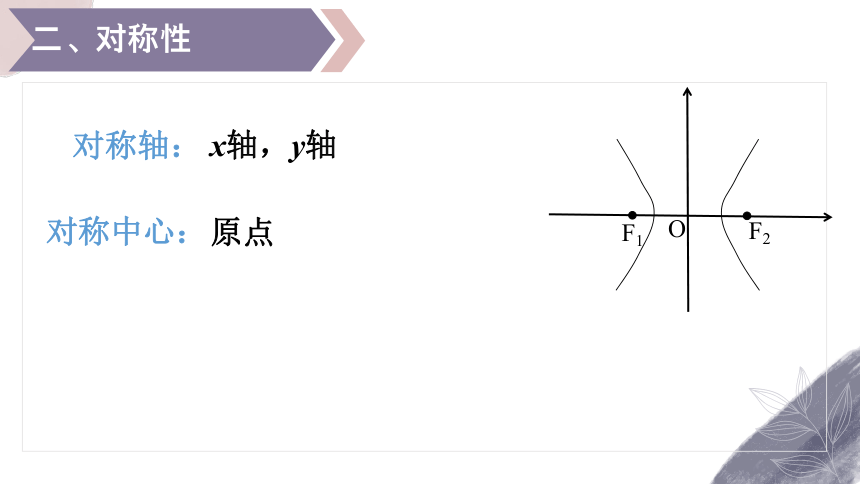
二、对称性
F1
F2
O
对称轴:
对称中心:
x轴,y轴
原点
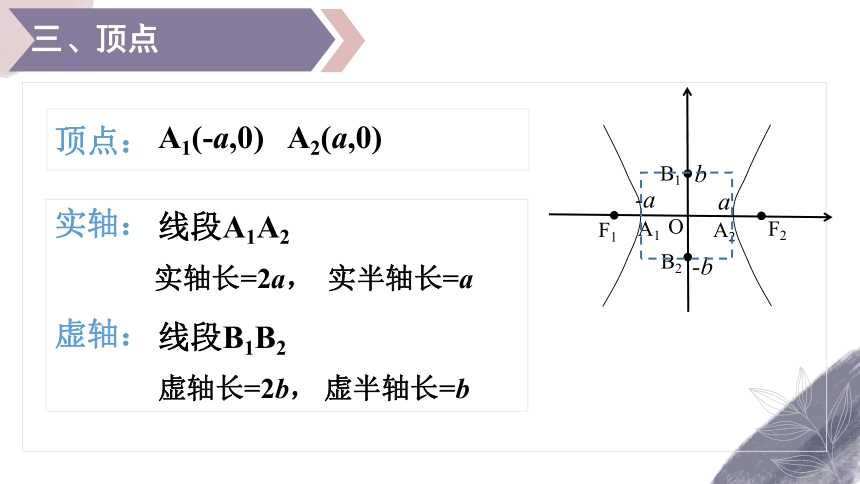
三、顶点
A1(-a,0) A2(a,0)
顶点:
实轴:
线段A1A2
虚轴:
线段B1B2
实轴长=2a,
实半轴长=a
虚轴长=2b,
虚半轴长=b
F1
F2
O
A1
A2
B1
B2
b
-b
-a
a
练习巩固
练习1 求下列双曲线的实轴和虚轴的长、顶点和焦点的坐标
(1)x2-8y2=32 (2)9x2-y2=81
(3)x2-y2=-4 (4)
练习巩固
练习1 求下列双曲线的实轴和虚轴的长、顶点和焦点的坐标
(1)x2-8y2=32 (2)9x2-y2=81
(3)x2-y2=-4 (4)
练习巩固
练习1 求下列双曲线的实轴和虚轴的长、顶点和焦点的坐标
(1)x2-8y2=32 (2)9x2-y2=81
(3)x2-y2=-4 (4)
练习巩固
练习1 求下列双曲线的实轴和虚轴的长、顶点和焦点的坐标
(1)x2-8y2=32 (2)9x2-y2=81
(3)x2-y2=-4 (4)
双曲线 (a>0,b>0)与直线有什么样的位置关系?
问题探究
F1
F2
O
A1
A2
B1
B2
b
-b
-a
a
四、渐近线
一般地,双曲线的两支向外延伸时,与两条直线逐渐接近,但永不相交.我们把这两条直线叫做双曲线的渐近线。
五、离心率
离心率:
e越接近1,双曲线开口越小;
e越大,双曲线开口越大.
y
B2
A1
A2
B1
x
O
F2
F1
练习巩固
例3 求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
六、等轴双曲线
若双曲线的实轴与虚轴相等,即a=b,则称为等轴双曲线.
等轴双曲线的方程:x2-y2=m (m≠0)
y
B2
A1
A2
B1
x
O
F2
F1
y
B2
A1
A2
B1
x
O
F2
F1
等轴双曲线的渐近线:y=±x
(两条渐近线相互垂直)
七、焦半径
y
B2
A1
A2
B1
x
O
F2
F1
P
焦半径:双曲线上的点到焦点的距离
八、通径
通径:过焦点且垂直长轴的弦
y
B2
A1
A2
B1
x
O
F2
F1
M
N
练习巩固
练习2 求符合下列条件的双曲线的标准方程
(1)顶点在x轴上,两顶点间的距离是8,
(2)焦点在y轴上,焦距是16,
练习巩固
练习2 求符合下列条件的双曲线的标准方程
(1)顶点在x轴上,两顶点间的距离是8,
(2)焦点在y轴上,焦距是16,
练习巩固
练习3 对称轴都在坐标轴上的等轴双曲线的一个焦点是
F1(-6,0),求双曲线的标准方程和渐近线方程。
练习巩固
练习4 双曲线的渐近线方程是y=±2x,虚轴长为4,求双曲线的标准方程
课堂小结
焦点位置 x轴 y轴
图像
焦点
顶点
轴 离心率 y
B2
A1
A2
B1
x
O
F2
F1
y
B2
A1
A2
B1
x
O
F2
F1
A1(-a,0) A2(a,0)
A1(0,-a) A2(0,a)
实轴长=2a,
虚轴长=2b,
F1(-c,0) F2(c,0)
F1(0,-c) F2(0,c)
e越大,开口越大;e越接近1,开口越小
课堂小结
焦点位置 x轴 y轴
图像
a,b,c关系 渐近线
焦半径 通径 y
B2
A1
A2
B1
x
O
F2
F1
y
B2
A1
A2
B1
x
O
F2
F1
a>0,b>0,且c2=a2+b2
过焦点且垂直长轴的弦
3.2 双曲线
3.2.2 双曲线的简单几何性质1
《悲伤的双曲线》
如果我是双曲线,你就是那渐近线。
如果我是反比例函数,你就是那坐标轴。
虽然我们有缘,能够生在同一个平面。
然而我们又无缘,漫漫长路无交点。
为何看不见,等式成立要条件。
难到正如书上说的,无限接近不能达到。
如果我是双曲线,你就是那渐近线。
#复习回顾
双曲线:在平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线。
||PF1|-|PF2||=2a < 2c
(a>0,b>0,且c2=a2+b2)
双曲线的标准方程:
焦点在x轴:
焦点在y轴:
类比椭圆的简单几何性质,你认为应该研究双曲线的哪些几何性质?
问题探究
一、范围
F1
F2
O
由方程
≥ 1
则 x ≤ -a或x≥ ≤ a
y ∈ R
二、对称性
F1
F2
O
对称轴:
对称中心:
x轴,y轴
原点
三、顶点
A1(-a,0) A2(a,0)
顶点:
实轴:
线段A1A2
虚轴:
线段B1B2
实轴长=2a,
实半轴长=a
虚轴长=2b,
虚半轴长=b
F1
F2
O
A1
A2
B1
B2
b
-b
-a
a
练习巩固
练习1 求下列双曲线的实轴和虚轴的长、顶点和焦点的坐标
(1)x2-8y2=32 (2)9x2-y2=81
(3)x2-y2=-4 (4)
练习巩固
练习1 求下列双曲线的实轴和虚轴的长、顶点和焦点的坐标
(1)x2-8y2=32 (2)9x2-y2=81
(3)x2-y2=-4 (4)
练习巩固
练习1 求下列双曲线的实轴和虚轴的长、顶点和焦点的坐标
(1)x2-8y2=32 (2)9x2-y2=81
(3)x2-y2=-4 (4)
练习巩固
练习1 求下列双曲线的实轴和虚轴的长、顶点和焦点的坐标
(1)x2-8y2=32 (2)9x2-y2=81
(3)x2-y2=-4 (4)
双曲线 (a>0,b>0)与直线有什么样的位置关系?
问题探究
F1
F2
O
A1
A2
B1
B2
b
-b
-a
a
四、渐近线
一般地,双曲线的两支向外延伸时,与两条直线逐渐接近,但永不相交.我们把这两条直线叫做双曲线的渐近线。
五、离心率
离心率:
e越接近1,双曲线开口越小;
e越大,双曲线开口越大.
y
B2
A1
A2
B1
x
O
F2
F1
练习巩固
例3 求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
六、等轴双曲线
若双曲线的实轴与虚轴相等,即a=b,则称为等轴双曲线.
等轴双曲线的方程:x2-y2=m (m≠0)
y
B2
A1
A2
B1
x
O
F2
F1
y
B2
A1
A2
B1
x
O
F2
F1
等轴双曲线的渐近线:y=±x
(两条渐近线相互垂直)
七、焦半径
y
B2
A1
A2
B1
x
O
F2
F1
P
焦半径:双曲线上的点到焦点的距离
八、通径
通径:过焦点且垂直长轴的弦
y
B2
A1
A2
B1
x
O
F2
F1
M
N
练习巩固
练习2 求符合下列条件的双曲线的标准方程
(1)顶点在x轴上,两顶点间的距离是8,
(2)焦点在y轴上,焦距是16,
练习巩固
练习2 求符合下列条件的双曲线的标准方程
(1)顶点在x轴上,两顶点间的距离是8,
(2)焦点在y轴上,焦距是16,
练习巩固
练习3 对称轴都在坐标轴上的等轴双曲线的一个焦点是
F1(-6,0),求双曲线的标准方程和渐近线方程。
练习巩固
练习4 双曲线的渐近线方程是y=±2x,虚轴长为4,求双曲线的标准方程
课堂小结
焦点位置 x轴 y轴
图像
焦点
顶点
轴 离心率 y
B2
A1
A2
B1
x
O
F2
F1
y
B2
A1
A2
B1
x
O
F2
F1
A1(-a,0) A2(a,0)
A1(0,-a) A2(0,a)
实轴长=2a,
虚轴长=2b,
F1(-c,0) F2(c,0)
F1(0,-c) F2(0,c)
e越大,开口越大;e越接近1,开口越小
课堂小结
焦点位置 x轴 y轴
图像
a,b,c关系 渐近线
焦半径 通径 y
B2
A1
A2
B1
x
O
F2
F1
y
B2
A1
A2
B1
x
O
F2
F1
a>0,b>0,且c2=a2+b2
过焦点且垂直长轴的弦
