沪科版七年级数学上册 第四章 直线与角 单元测试卷 (含答案)
文档属性
| 名称 | 沪科版七年级数学上册 第四章 直线与角 单元测试卷 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 165.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 09:50:22 | ||
图片预览



文档简介
第四章《直线与角》单元测试卷
一、选择题(每题4分,共40分)
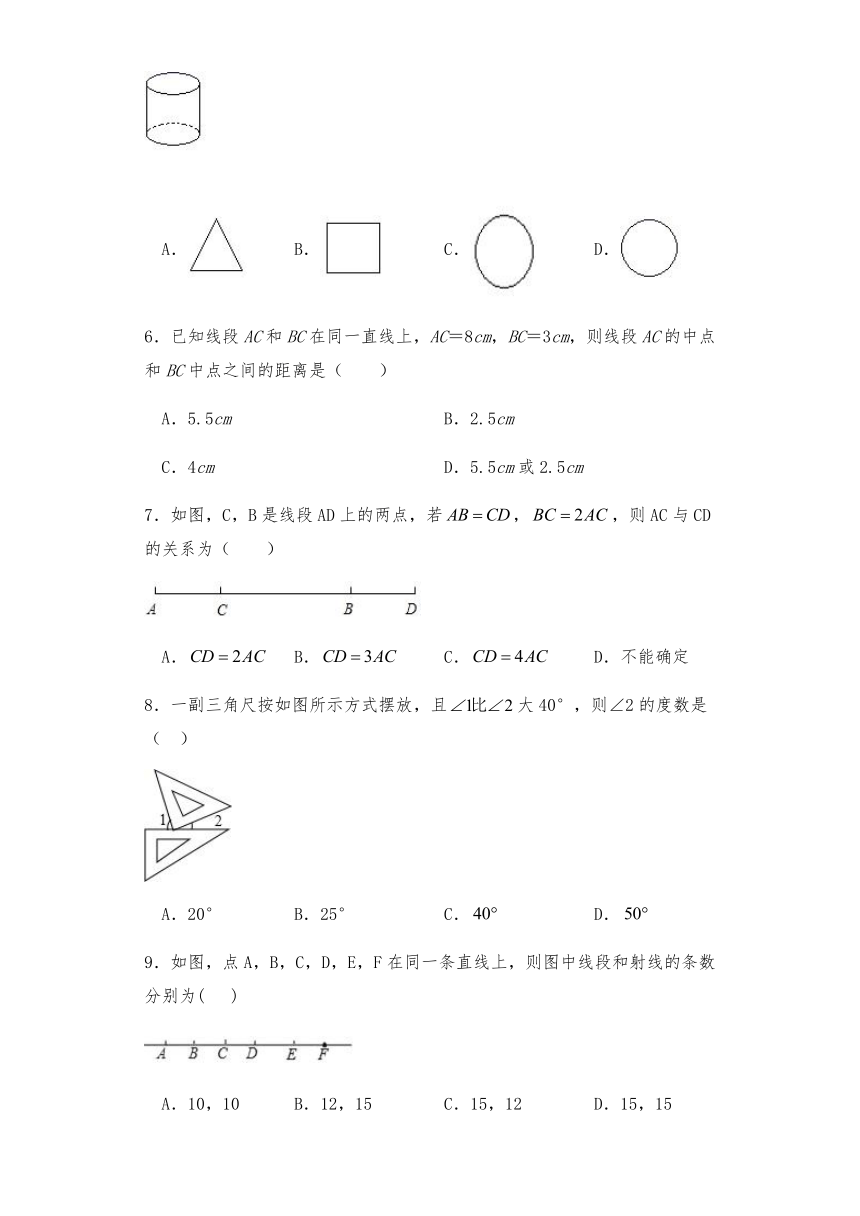
1.如图是某个几何体的展开图,该几何体是( )
A.三棱柱 B.圆锥 C.四棱柱 D.圆柱
2.平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b的值是( )
A. B. C. D.
3.下列说法:①经过一点有无数条直线;②两点之间线段最短;③经过两点,有且只有一条直线;④若线段AM等于线段BM,则点M是线段AB的中点;⑤连接两点的线段叫做这两点之间的距离.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
4.高速公路的建设带动我国经济的快速发展.在高速公路的建设中,通常要从大山中开挖隧道穿过,把道路取直,以缩短路程.这样做包含的数学道理是( )
A.两点确定一条直线 B.两点之间,线段最短
C.两条直线相交,只有一个交点 D.直线是向两个方向无限延伸的
5.如右图,是一块圆柱体形状的木头,用锯子把这个圆柱体锯成两部分,锯开的这个面不可能是( )
A. B. C. D.
6.已知线段AC和BC在同一直线上,AC=8cm,BC=3cm,则线段AC的中点和BC中点之间的距离是( )
A.5.5cm B.2.5cm
C.4cm D.5.5cm或2.5cm
7.如图,C,B是线段AD上的两点,若,,则AC与CD的关系为( )
A. B. C. D.不能确定
8.一副三角尺按如图所示方式摆放,且大40°,则∠2的度数是( )
A.20° B.25° C. D.
9.如图,点A,B,C,D,E,F在同一条直线上,则图中线段和射线的条数分别为( )
A.10,10 B.12,15 C.15,12 D.15,15
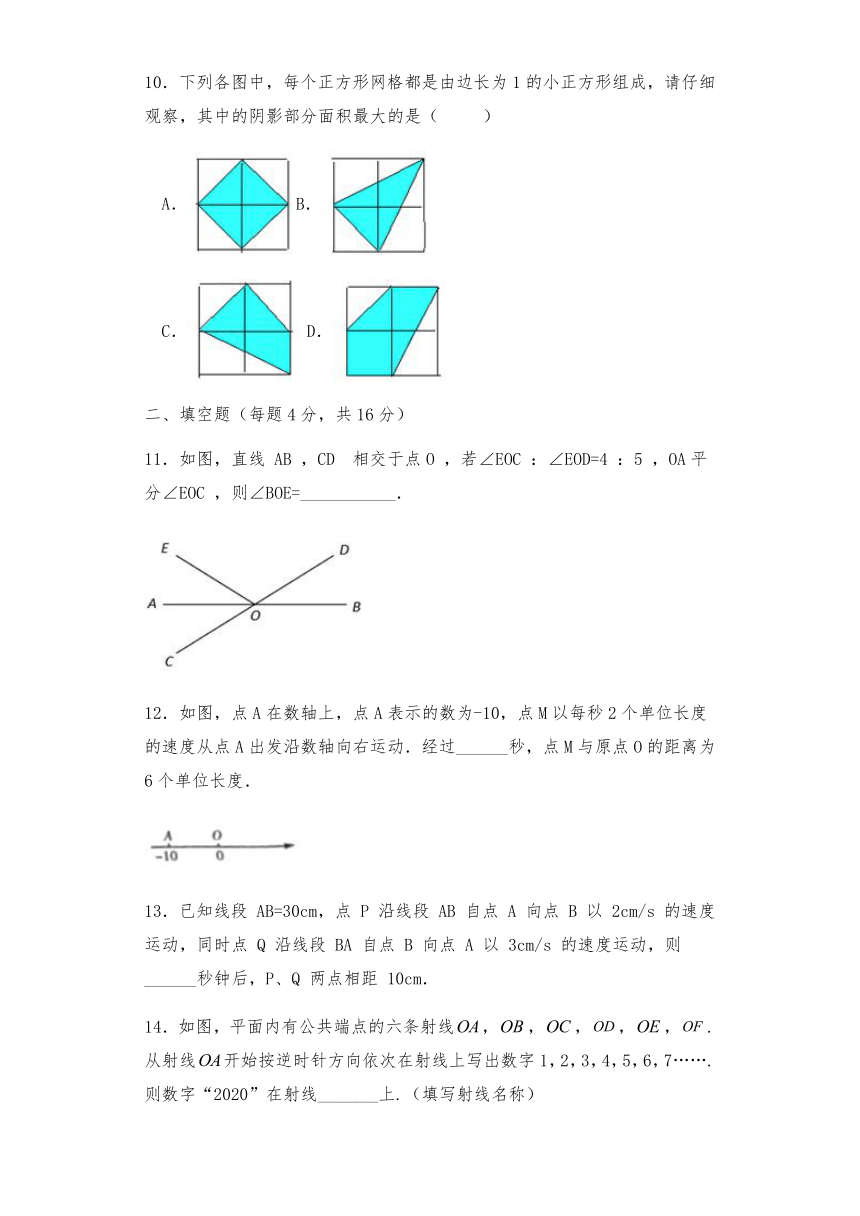
10.下列各图中,每个正方形网格都是由边长为1的小正方形组成,请仔细观察,其中的阴影部分面积最大的是( )
A.B.
C.D.
二、填空题(每题4分,共16分)
11.如图,直线 AB ,CD 相交于点O ,若∠EOC :∠EOD=4 :5 ,OA平分∠EOC ,则∠BOE=___________.
12.如图,点A在数轴上,点A表示的数为-10,点M以每秒2个单位长度的速度从点A出发沿数轴向右运动.经过______秒,点M与原点O的距离为6个单位长度.
13.已知线段 AB=30cm,点 P 沿线段 AB 自点 A 向点 B 以 2cm/s 的速度运动,同时点 Q 沿线段 BA 自点 B 向点 A 以 3cm/s 的速度运动,则______秒钟后,P、Q 两点相距 10cm.
14.如图,平面内有公共端点的六条射线,,,,,.从射线开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7…….则数字“2020”在射线_______上.(填写射线名称)
三、解答题(共64分)
15.如图,已知线段AB和CD的公共部分BD=AB=CD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长.
16.如图,已知A、O、B三点共线,∠AOD=42°,∠COB=90°.
(1)求∠BOD的度数;
(2)若OE平分∠BOD,求∠COE的度数.
17.如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
18.如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=AB时,求t的值.
19.如图所示,已知线段AB=6cm,C是AB的中点,点D在AC上,且CD=2AD,E是BC的中点,求线段DE的长.
20.如图,线段,点E,F分别是线段AB,CD的中点, cm,求线段AB,CD的长.
21.如图,已知A,B,C是数轴上三点,点C表示的数为6,BC=4,AB=12.
(1)写出数轴上点A,B表示的数.
(2)动点P,Q分别从A,C同时出发,点P以每秒6个单位长度的速度沿数轴向右匀速运动,点Q以每秒3个单位长度的速度沿数轴向左匀速运动.若M为AP的中点,点N在线段CQ上,且CN=CQ,设运动时间为ts(t>0).
①写出数轴上点M,N表示的数(用含t的式子表示).
②t为何值时,原点O恰为线段PQ的中点
22.如图,B是线段AD上一动点,沿A→D→A以 2 cm/s的速度往返运动1次,C是线段BD的中点,AD=10 cm,设点B的运动时间为t秒(0≤t≤10).
(1)当t=2时,
①AB=____cm;
②求线段CD的长度;
(2)用含t的代数式表示运动过程中AB的长;
(3)在运动过程中,若AB的中点为E,则EC的长是否变化?若不变,求出EC的长;若发生变化,请说明理由.
23.如图,∠AOB=90°,射线OM平分∠AOC,ON平分∠BOC.
(1)如果∠BOC=30°,求∠MON的度数;
(2)如果∠AOB=α,∠BOC=30°,其他条件不变,求∠MON的度数;
答案
一、选择题
A.D.C.B.A.D.B.B.C.D.
二、填空题
11.140°
12.2或8
13.4或8
14.OD.
三、解答题
15.
解:设BD=xcm,则AB=3xcm,CD=4xcm,AC=6xcm.
∵点E、点F分别为AB、CD的中点,
∴AE=AB=1.5xcm,CF=CD=2xcm.
∴EF=AC-AE-CF=2.5xcm.
∵EF=10cm,
∴2.5x=10,解得:x=4.
∴AB=12cm,CD=16cm.
16.
(1)∵A、O、B三点共线,∠AOD=42°,
∴∠BOD=180°﹣∠AOD=138°;
(2)∵∠COB=90°,
∴∠AOC=90°,
∵∠AOD=42°,
∴∠COD=48°,
∵OE平分∠BOD,
∴∠DOE=∠BOD=69°,
∴∠COE=69°﹣48°=21°.
17.
(1)∵线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点,
∴CM=AC=5厘米,CN=BC=3厘米,
∴MN=CM+CN=8厘米;
(2)∵点M,N分别是AC,BC的中点,
∴CM=AC,CN=BC,
∴MN=CM+CN=AC+BC=a;
(3)①当0<t≤5时,C是线段PQ的中点,得
10﹣2t=6﹣t,解得t=4;
②当5<t≤时,P为线段CQ的中点,2t﹣10=16﹣3t,解得t=;
③当<t≤6时,Q为线段PC的中点,6﹣t=3t﹣16,解得t=;
④当6<t≤8时,C为线段PQ的中点,2t﹣10=t﹣6,解得t=4(舍),
综上所述:t=4或或.
18.解:(1)∵当0<t<5时,P点对应的有理数为10+t<15,Q点对应的有理数为2t<10,∴BP=15﹣(10+t)=5﹣t,AQ=10﹣2t.
故答案为:5﹣t,10﹣2t;
(2)当t=2时,P点对应的有理数为10+2=12,Q点对应的有理数为2×2=4,所以PQ=12﹣4=8;
(3)∵t秒时,P点对应的有理数为10+t,Q点对应的有理数为2t,∴PQ=|2t﹣(10+t)|=|t﹣10|,∵PQ=AB,∴|t﹣10|=2.5,解得t=12.5或7.5.
19.
∵AB=6cm,C是AB中点,
∴AC=BC=AB=3cm,
又∵AB=6cm,
∴AC=BC==3cm ,
∵E是BC中点,
∴CE=BC=1.5cm,
∵CD=2AD AD+DC=AC,
∴AD+2AD=AC=3AD,
∴AD=1cm,CD=2cm,
∴DE=CD+CE= 2+1.5=3.5cm.
20.
解:因为,设BD=x,则CD=5x,AB=4x,
∵点E,F分别是AB,CD的中点,
∴EB= AB=2x,DF=CD=2.5x,
∴ED=x,
∴EF=ED+DF=3.5x,
又∵EF=14,
∴3.5x=14,
解得x=4,
∴CD=5x=20cm,AB=4x=16cm.
21.
(1)∵C表示的数为6,BC=4,
∴OB=6-4=2,
∴B点表示2,
∵AB=12,
∴AO=12-2=10,
∴A点表示-10;
(2)①由题意得:AP=6t,CQ=3t,
∵M为AP中点,
∴AM=AP=3t,
∴在数轴上点M表示的数是-10+3t,
∵点N在CQ上,CN=CQ,
∴CN=t.
∴在数轴上点N表示的数是6-t.
②∵原点O恰为线段PQ的中点,
∴OP=OQ,
∵OP=-10+6t,OQ=6-3t,
∴-10+6t与6-3t互为相反数,
∴-10+6t=-(6-3t),
解得:t=,
∴t=时,原点O恰为线段PQ的中点.
22.解:(1)①当t=2时,AB=2t=2×2=4(cm);
②∵AD=10 cm,AB=4 cm,
∴BD=10-4=6(cm).
∵C是线段BD的中点,
∴CD=BD=×6=3(cm).
(2)∵B是线段AD上一动点,沿A→D→A以2 m/s的速度往返运动,
∴0≤t≤5时,AB=2t cm;
5(3)不变.
∵AB的中点为E,C是线段BD的中点,
∴EC= (AB+BD)=AD=×10=5(cm).
23.
(1)由题意得,
∵ON平分∠BOC,∠BOC=30°
∴∠BOC=2∠NOC
∴∠NOC=15°
∵OM平分∠AOC
∴∠MOC=∠AOC
∵∠AOC=90°+∠BOC=90°+30°=120°,
∴∠MOC═∠AOC=×120°=60°
∴∠MON=∠MOC-∠NOC=60°-15°=45°
故∠MON的度数为45°
(2)
由(1)同理可得,∠NOC=15°
∵∠AOB=α
∵∠AOC=α+∠BOC=α+30°
∴∠MOC═∠AOC=×(α+30°)=α+15°
∴∠MON=∠MOC-∠NOC=α+15° 15°=α
故∠MON的度数为α
一、选择题(每题4分,共40分)
1.如图是某个几何体的展开图,该几何体是( )
A.三棱柱 B.圆锥 C.四棱柱 D.圆柱
2.平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b的值是( )
A. B. C. D.
3.下列说法:①经过一点有无数条直线;②两点之间线段最短;③经过两点,有且只有一条直线;④若线段AM等于线段BM,则点M是线段AB的中点;⑤连接两点的线段叫做这两点之间的距离.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
4.高速公路的建设带动我国经济的快速发展.在高速公路的建设中,通常要从大山中开挖隧道穿过,把道路取直,以缩短路程.这样做包含的数学道理是( )
A.两点确定一条直线 B.两点之间,线段最短
C.两条直线相交,只有一个交点 D.直线是向两个方向无限延伸的
5.如右图,是一块圆柱体形状的木头,用锯子把这个圆柱体锯成两部分,锯开的这个面不可能是( )
A. B. C. D.
6.已知线段AC和BC在同一直线上,AC=8cm,BC=3cm,则线段AC的中点和BC中点之间的距离是( )
A.5.5cm B.2.5cm
C.4cm D.5.5cm或2.5cm
7.如图,C,B是线段AD上的两点,若,,则AC与CD的关系为( )
A. B. C. D.不能确定
8.一副三角尺按如图所示方式摆放,且大40°,则∠2的度数是( )
A.20° B.25° C. D.
9.如图,点A,B,C,D,E,F在同一条直线上,则图中线段和射线的条数分别为( )
A.10,10 B.12,15 C.15,12 D.15,15
10.下列各图中,每个正方形网格都是由边长为1的小正方形组成,请仔细观察,其中的阴影部分面积最大的是( )
A.B.
C.D.
二、填空题(每题4分,共16分)
11.如图,直线 AB ,CD 相交于点O ,若∠EOC :∠EOD=4 :5 ,OA平分∠EOC ,则∠BOE=___________.
12.如图,点A在数轴上,点A表示的数为-10,点M以每秒2个单位长度的速度从点A出发沿数轴向右运动.经过______秒,点M与原点O的距离为6个单位长度.
13.已知线段 AB=30cm,点 P 沿线段 AB 自点 A 向点 B 以 2cm/s 的速度运动,同时点 Q 沿线段 BA 自点 B 向点 A 以 3cm/s 的速度运动,则______秒钟后,P、Q 两点相距 10cm.
14.如图,平面内有公共端点的六条射线,,,,,.从射线开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7…….则数字“2020”在射线_______上.(填写射线名称)
三、解答题(共64分)
15.如图,已知线段AB和CD的公共部分BD=AB=CD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长.
16.如图,已知A、O、B三点共线,∠AOD=42°,∠COB=90°.
(1)求∠BOD的度数;
(2)若OE平分∠BOD,求∠COE的度数.
17.如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
18.如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=AB时,求t的值.
19.如图所示,已知线段AB=6cm,C是AB的中点,点D在AC上,且CD=2AD,E是BC的中点,求线段DE的长.
20.如图,线段,点E,F分别是线段AB,CD的中点, cm,求线段AB,CD的长.
21.如图,已知A,B,C是数轴上三点,点C表示的数为6,BC=4,AB=12.
(1)写出数轴上点A,B表示的数.
(2)动点P,Q分别从A,C同时出发,点P以每秒6个单位长度的速度沿数轴向右匀速运动,点Q以每秒3个单位长度的速度沿数轴向左匀速运动.若M为AP的中点,点N在线段CQ上,且CN=CQ,设运动时间为ts(t>0).
①写出数轴上点M,N表示的数(用含t的式子表示).
②t为何值时,原点O恰为线段PQ的中点
22.如图,B是线段AD上一动点,沿A→D→A以 2 cm/s的速度往返运动1次,C是线段BD的中点,AD=10 cm,设点B的运动时间为t秒(0≤t≤10).
(1)当t=2时,
①AB=____cm;
②求线段CD的长度;
(2)用含t的代数式表示运动过程中AB的长;
(3)在运动过程中,若AB的中点为E,则EC的长是否变化?若不变,求出EC的长;若发生变化,请说明理由.
23.如图,∠AOB=90°,射线OM平分∠AOC,ON平分∠BOC.
(1)如果∠BOC=30°,求∠MON的度数;
(2)如果∠AOB=α,∠BOC=30°,其他条件不变,求∠MON的度数;
答案
一、选择题
A.D.C.B.A.D.B.B.C.D.
二、填空题
11.140°
12.2或8
13.4或8
14.OD.
三、解答题
15.
解:设BD=xcm,则AB=3xcm,CD=4xcm,AC=6xcm.
∵点E、点F分别为AB、CD的中点,
∴AE=AB=1.5xcm,CF=CD=2xcm.
∴EF=AC-AE-CF=2.5xcm.
∵EF=10cm,
∴2.5x=10,解得:x=4.
∴AB=12cm,CD=16cm.
16.
(1)∵A、O、B三点共线,∠AOD=42°,
∴∠BOD=180°﹣∠AOD=138°;
(2)∵∠COB=90°,
∴∠AOC=90°,
∵∠AOD=42°,
∴∠COD=48°,
∵OE平分∠BOD,
∴∠DOE=∠BOD=69°,
∴∠COE=69°﹣48°=21°.
17.
(1)∵线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点,
∴CM=AC=5厘米,CN=BC=3厘米,
∴MN=CM+CN=8厘米;
(2)∵点M,N分别是AC,BC的中点,
∴CM=AC,CN=BC,
∴MN=CM+CN=AC+BC=a;
(3)①当0<t≤5时,C是线段PQ的中点,得
10﹣2t=6﹣t,解得t=4;
②当5<t≤时,P为线段CQ的中点,2t﹣10=16﹣3t,解得t=;
③当<t≤6时,Q为线段PC的中点,6﹣t=3t﹣16,解得t=;
④当6<t≤8时,C为线段PQ的中点,2t﹣10=t﹣6,解得t=4(舍),
综上所述:t=4或或.
18.解:(1)∵当0<t<5时,P点对应的有理数为10+t<15,Q点对应的有理数为2t<10,∴BP=15﹣(10+t)=5﹣t,AQ=10﹣2t.
故答案为:5﹣t,10﹣2t;
(2)当t=2时,P点对应的有理数为10+2=12,Q点对应的有理数为2×2=4,所以PQ=12﹣4=8;
(3)∵t秒时,P点对应的有理数为10+t,Q点对应的有理数为2t,∴PQ=|2t﹣(10+t)|=|t﹣10|,∵PQ=AB,∴|t﹣10|=2.5,解得t=12.5或7.5.
19.
∵AB=6cm,C是AB中点,
∴AC=BC=AB=3cm,
又∵AB=6cm,
∴AC=BC==3cm ,
∵E是BC中点,
∴CE=BC=1.5cm,
∵CD=2AD AD+DC=AC,
∴AD+2AD=AC=3AD,
∴AD=1cm,CD=2cm,
∴DE=CD+CE= 2+1.5=3.5cm.
20.
解:因为,设BD=x,则CD=5x,AB=4x,
∵点E,F分别是AB,CD的中点,
∴EB= AB=2x,DF=CD=2.5x,
∴ED=x,
∴EF=ED+DF=3.5x,
又∵EF=14,
∴3.5x=14,
解得x=4,
∴CD=5x=20cm,AB=4x=16cm.
21.
(1)∵C表示的数为6,BC=4,
∴OB=6-4=2,
∴B点表示2,
∵AB=12,
∴AO=12-2=10,
∴A点表示-10;
(2)①由题意得:AP=6t,CQ=3t,
∵M为AP中点,
∴AM=AP=3t,
∴在数轴上点M表示的数是-10+3t,
∵点N在CQ上,CN=CQ,
∴CN=t.
∴在数轴上点N表示的数是6-t.
②∵原点O恰为线段PQ的中点,
∴OP=OQ,
∵OP=-10+6t,OQ=6-3t,
∴-10+6t与6-3t互为相反数,
∴-10+6t=-(6-3t),
解得:t=,
∴t=时,原点O恰为线段PQ的中点.
22.解:(1)①当t=2时,AB=2t=2×2=4(cm);
②∵AD=10 cm,AB=4 cm,
∴BD=10-4=6(cm).
∵C是线段BD的中点,
∴CD=BD=×6=3(cm).
(2)∵B是线段AD上一动点,沿A→D→A以2 m/s的速度往返运动,
∴0≤t≤5时,AB=2t cm;
5
∵AB的中点为E,C是线段BD的中点,
∴EC= (AB+BD)=AD=×10=5(cm).
23.
(1)由题意得,
∵ON平分∠BOC,∠BOC=30°
∴∠BOC=2∠NOC
∴∠NOC=15°
∵OM平分∠AOC
∴∠MOC=∠AOC
∵∠AOC=90°+∠BOC=90°+30°=120°,
∴∠MOC═∠AOC=×120°=60°
∴∠MON=∠MOC-∠NOC=60°-15°=45°
故∠MON的度数为45°
(2)
由(1)同理可得,∠NOC=15°
∵∠AOB=α
∵∠AOC=α+∠BOC=α+30°
∴∠MOC═∠AOC=×(α+30°)=α+15°
∴∠MON=∠MOC-∠NOC=α+15° 15°=α
故∠MON的度数为α
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
