沪科版七年级数学上册 2.2整式加减 同步练习(2课时 含答案)
文档属性
| 名称 | 沪科版七年级数学上册 2.2整式加减 同步练习(2课时 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 201.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 09:55:21 | ||
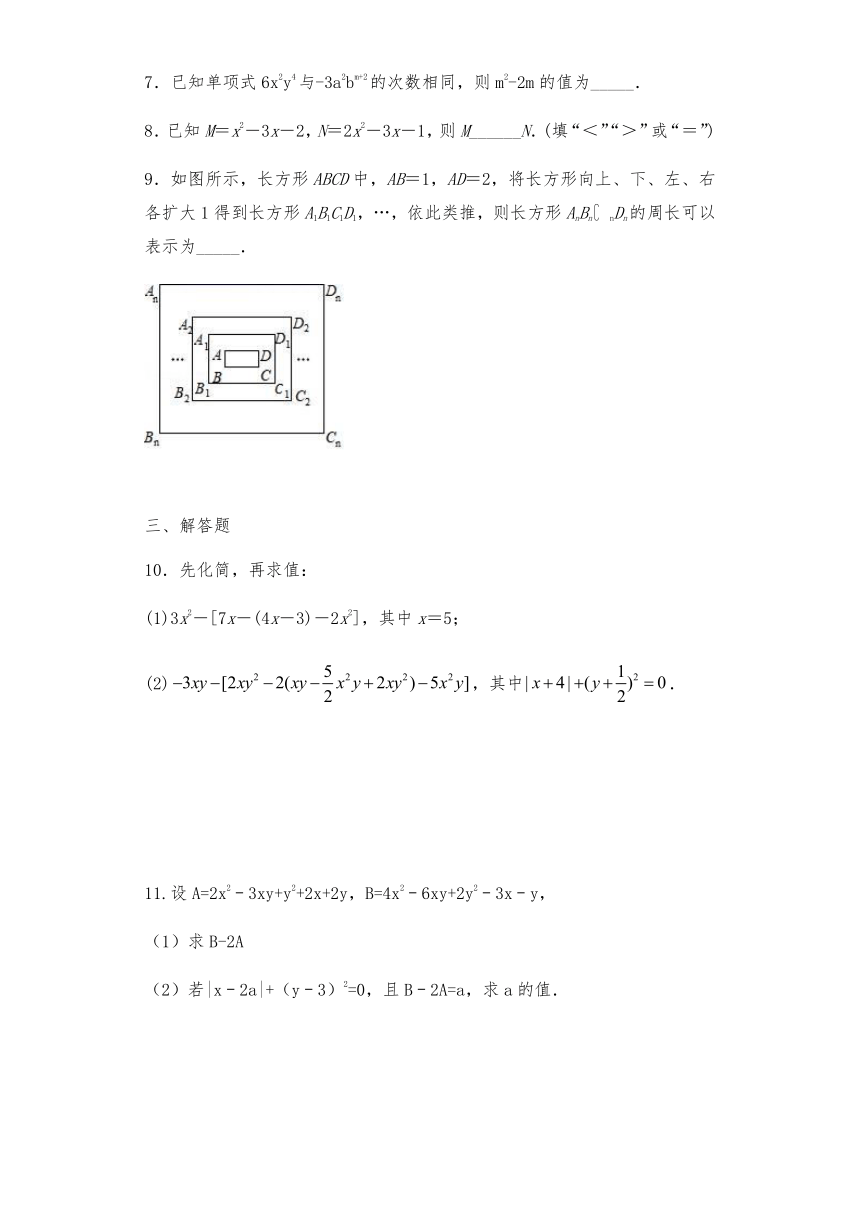
图片预览



文档简介
2.2整式加减
第一课时
一、单选题
1.已知一个多项式与3x2+9x的和等于3x2+4x﹣1,则这个多项式是( )
A.﹣5x﹣1 B.5x+1 C.﹣13x﹣1 D.13x+1
2.下面计算正确的是( )
A.6a-5a=1 B.a+2a2=3a2
C.-(a-b)=-a+b D.2(a+b)=2a+b
3.单项式xm﹣1y3与4xyn的和是单项式,则nm 的值是( )
A.3 B.6 C.8 D.9
4.多项式8x2﹣3x+5与3x3﹣4mx2﹣5x+7多项式相加后,不含二次项,则m的值是( )
A.2 B.4 C.﹣2 D.﹣4
5.若代数式b为常数的值与字母x的取值无关,则代数式的值为
A.0 B. C.2或 D.6
二、填空题
6.单项式﹣π2x2y的系数是_____,次数是_____.
7.若与是同类项,则=______.
8.在代数式,-3xy3,0,4ab,3x2-4,,n中,单项式有____个.
9.己知多项式,,且多项式中不含字母,则的值为__________.
三、解答题
10.一位同学一道题:“已知两个多项式,,计算”,他误将看成,求得的结果为,已知
(1)求多项式;
(2)请你求出的正确答案.
11.化简:-a2 b +(3ab2-a2b)- 2(2ab2-a2b)
12.先化简,再求值:2xy-(4xy-8x2y2)+2(3xy-5x2y2),其中x=,y=-3.
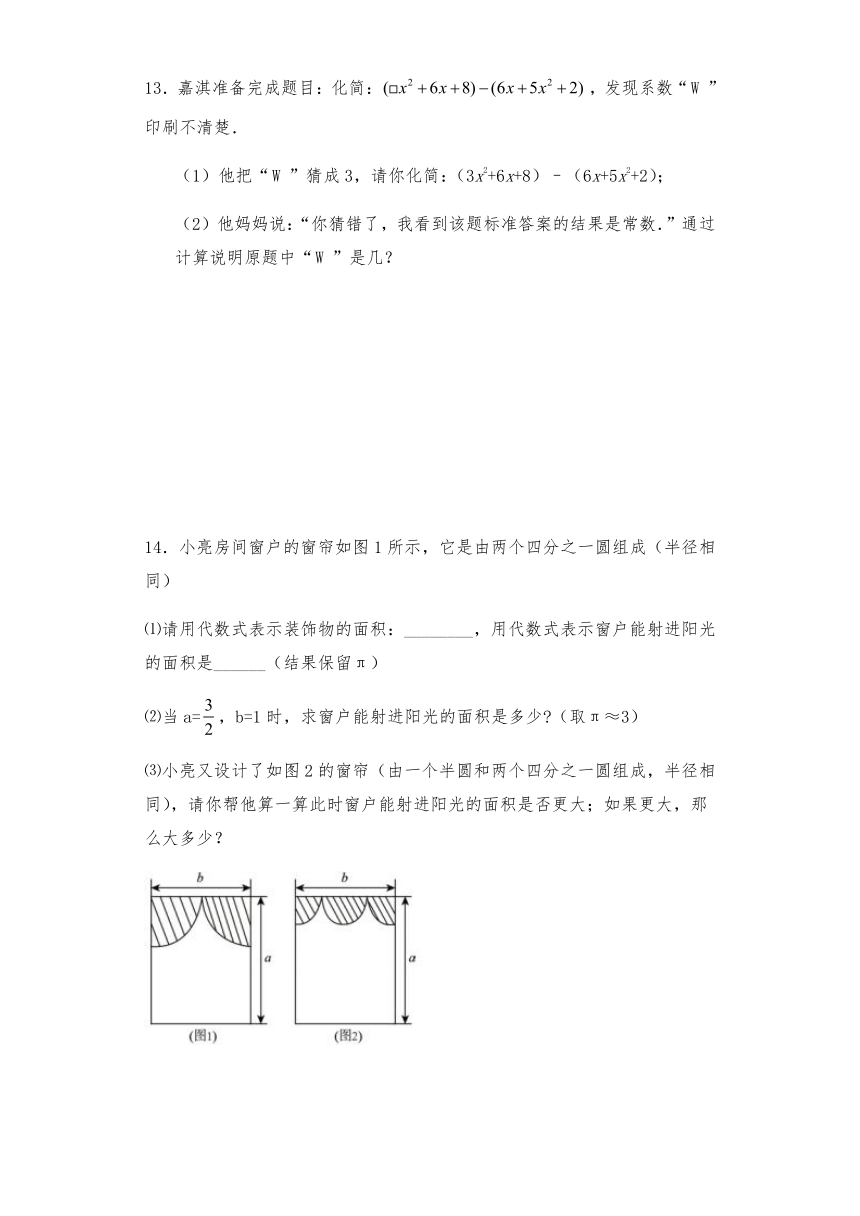
13.嘉淇准备完成题目:化简:,发现系数“”印刷不清楚.
(1)他把“”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“”是几?
14.小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)
⑴请用代数式表示装饰物的面积:________,用代数式表示窗户能射进阳光的面积是______(结果保留π)
⑵当a=,b=1时,求窗户能射进阳光的面积是多少 (取π≈3)
⑶小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大;如果更大,那么大多少?
第二课时
一、单选题
1.若单项式am﹣1b2与的和仍是单项式,则nm的值是( )
A.3 B.6 C.8 D.9
2.如图所示,、是有理数,则式子化简的结果为( )
A.3+ B.3- C.3+ D.3-
3.下列计算正确的是( )
A.a2 a=a2 B.a6÷a2=a3
C.a2b﹣2ba2=﹣a2b D.(﹣)3=﹣
4.已知m,n为常数,代数式2x4y+mx|5-n|y+xy化简之后为单项式,则mn的值共有( )
A.1个 B.2个 C.3个 D.4个
5.萱萱的妈妈下岗了,在国家政策的扶持下开了一家商店,全家每个人都要出一份力,妈妈告诉萱萱说,她第一次进货时以每件元的价格购进了件牛奶;每件元的价格购进了件洗发水,萱萱建议将这两种商品都以元的价格出售,则按萱萱的建议商品卖出后,商店( )
A.赚钱 B.赔钱
C.不嫌不赔 D.无法确定赚与赔
二、填空题
6.若关于x、y的代数式mx3﹣3nxy2+2x3﹣xy2+y中不含三次项,则(m﹣3n)2018=_____.
7.已知单项式6x2y4与-3a2bm+2的次数相同,则m2-2m的值为_____.
8.已知M=x2-3x-2,N=2x2-3x-1,则M______N.(填“<”“>”或“=”)
9.如图所示,长方形ABCD中,AB=1,AD=2,将长方形向上、下、左、右各扩大1得到长方形A1B1C1D1,…,依此类推,则长方形AnBn nDn的周长可以表示为_____.
三、解答题
10.先化简,再求值:
(1)3x2-[7x-(4x-3)-2x2],其中x=5;
(2),其中.
11.设A=2x2﹣3xy+y2+2x+2y,B=4x2﹣6xy+2y2﹣3x﹣y,
(1)求B-2A
(2)若|x﹣2a|+(y﹣3)2=0,且B﹣2A=a,求a的值.
12.已知A=2x2+3xy+2x﹣1,B=x2+xy+3x﹣2.
(1)当x=y=﹣2时,求A﹣2B的值;
(2)若A﹣2B的值与x无关,求y的值.
13.已知有理数,在数轴上的位置如图所示,化简:.
14.阅读材料:对于任何数,我们规定符号 的意义是 =ad﹣bc
例如: =1×4﹣2×3=﹣2
(1)按照这个规定,请你计算 的值.
(2)按照这个规定,请你计算当|x+y-4|+(xy+1)2=0时, 的值.
第一课时答案
一、单选题
A.C.D.A.B
二、填空题
6.﹣π2 3
7.-1.
8.5
9.1
三、解答题
10.
解:(1)
(2)
11.原式= -a2b +3ab2-a2b- 4ab2+2a2b = - ab2 .
12.
解:原式=2xy-2xy+4x2y2+6xy-10x2y2=6xy-6x2y2.
当x=,y=-3时,原式=6××(-3)-6×()2×(-3)2=-6-6=-12.
13.(1)(3x2+6x+8)﹣(6x+5x2+2)
=3x2+6x+8﹣6x﹣5x2﹣2
=﹣2x2+6;
(2)设“”是a,
则原式=(ax2+6x+8)﹣(6x+5x2+2)
=ax2+6x+8﹣6x﹣5x2﹣2
=(a﹣5)x2+6,
∵标准答案的结果是常数,
∴a﹣5=0,
解得:a=5.
14.
解:(1)装饰物的面积为:π()2=b2,窗户能射进阳光的面积是: ab-b2;
故答案为:,;
(2)ab-b2=×1-×1
=-
=
(3)更大了,
窗帘的面积:π()2=b2 ,
( ab-b2)-(ab-b2)=b2-b2=b2
∴此时窗户能射进阳光的面积更大了,大b2.
第二课时答案
一、单选题
C.D.C.C.D.
二、填空题
6.1
7.0
8.<
9.8n+6.
三、解答题
10.
(1)原式=5x2-3x-3
∵x=5,
∴原式=107
(2)原式=-3xy-2xy2+2xy-5x2y +4xy 2+5x2y
=-xy+2xy 2
由得x=-4 y=- ,
∴原式=-(-4)×(-)+2×(-4)×(-)2=-2-2=-4.
11.解:(1)、B﹣2A=4x2﹣6xy+2y2﹣3x﹣y﹣2(2x2﹣3xy+y2+2x+2y)
=4x2﹣6xy+2y2﹣3x﹣y﹣4x2+6xy﹣2y2﹣4x﹣4y=﹣7x﹣5y
(2)、∵|x﹣2a|+(y﹣3)2=0 ∴x=2a,y=3
又B﹣2A=a, ∴﹣7×2a﹣5×3=a, ∴a=﹣1.
12.A﹣2B=(2x2+3xy+2x﹣1)﹣2(x2+xy+3x﹣2)=xy﹣4x+3,
(1)当x=y=﹣2时,A﹣2B=(﹣2)×(﹣2)﹣4×(﹣2)+3=15;
(2)A﹣2B=xy﹣4x+3=(y﹣4)x+3
∵A﹣2B的值与x无关,
∴y﹣4=0,
解得:y=4.
13.
解:由数轴可知:,
∴,,,
∴原式,
,
.
故答案为.
14.
解:(1) =5×8﹣(-2)×6=52.
(2)由|x+y-4|+(xy+1)2=0得x+y-4=0,∴xy+1=0. x+y=4,∴xy=-1.
∴ =2x+1+3xy+2y=2(x+y)+3xy+1=2×4+3×(-1)+1=6.
第一课时
一、单选题
1.已知一个多项式与3x2+9x的和等于3x2+4x﹣1,则这个多项式是( )
A.﹣5x﹣1 B.5x+1 C.﹣13x﹣1 D.13x+1
2.下面计算正确的是( )
A.6a-5a=1 B.a+2a2=3a2
C.-(a-b)=-a+b D.2(a+b)=2a+b
3.单项式xm﹣1y3与4xyn的和是单项式,则nm 的值是( )
A.3 B.6 C.8 D.9
4.多项式8x2﹣3x+5与3x3﹣4mx2﹣5x+7多项式相加后,不含二次项,则m的值是( )
A.2 B.4 C.﹣2 D.﹣4
5.若代数式b为常数的值与字母x的取值无关,则代数式的值为
A.0 B. C.2或 D.6
二、填空题
6.单项式﹣π2x2y的系数是_____,次数是_____.
7.若与是同类项,则=______.
8.在代数式,-3xy3,0,4ab,3x2-4,,n中,单项式有____个.
9.己知多项式,,且多项式中不含字母,则的值为__________.
三、解答题
10.一位同学一道题:“已知两个多项式,,计算”,他误将看成,求得的结果为,已知
(1)求多项式;
(2)请你求出的正确答案.
11.化简:-a2 b +(3ab2-a2b)- 2(2ab2-a2b)
12.先化简,再求值:2xy-(4xy-8x2y2)+2(3xy-5x2y2),其中x=,y=-3.
13.嘉淇准备完成题目:化简:,发现系数“”印刷不清楚.
(1)他把“”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“”是几?
14.小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)
⑴请用代数式表示装饰物的面积:________,用代数式表示窗户能射进阳光的面积是______(结果保留π)
⑵当a=,b=1时,求窗户能射进阳光的面积是多少 (取π≈3)
⑶小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大;如果更大,那么大多少?
第二课时
一、单选题
1.若单项式am﹣1b2与的和仍是单项式,则nm的值是( )
A.3 B.6 C.8 D.9
2.如图所示,、是有理数,则式子化简的结果为( )
A.3+ B.3- C.3+ D.3-
3.下列计算正确的是( )
A.a2 a=a2 B.a6÷a2=a3
C.a2b﹣2ba2=﹣a2b D.(﹣)3=﹣
4.已知m,n为常数,代数式2x4y+mx|5-n|y+xy化简之后为单项式,则mn的值共有( )
A.1个 B.2个 C.3个 D.4个
5.萱萱的妈妈下岗了,在国家政策的扶持下开了一家商店,全家每个人都要出一份力,妈妈告诉萱萱说,她第一次进货时以每件元的价格购进了件牛奶;每件元的价格购进了件洗发水,萱萱建议将这两种商品都以元的价格出售,则按萱萱的建议商品卖出后,商店( )
A.赚钱 B.赔钱
C.不嫌不赔 D.无法确定赚与赔
二、填空题
6.若关于x、y的代数式mx3﹣3nxy2+2x3﹣xy2+y中不含三次项,则(m﹣3n)2018=_____.
7.已知单项式6x2y4与-3a2bm+2的次数相同,则m2-2m的值为_____.
8.已知M=x2-3x-2,N=2x2-3x-1,则M______N.(填“<”“>”或“=”)
9.如图所示,长方形ABCD中,AB=1,AD=2,将长方形向上、下、左、右各扩大1得到长方形A1B1C1D1,…,依此类推,则长方形AnBn nDn的周长可以表示为_____.
三、解答题
10.先化简,再求值:
(1)3x2-[7x-(4x-3)-2x2],其中x=5;
(2),其中.
11.设A=2x2﹣3xy+y2+2x+2y,B=4x2﹣6xy+2y2﹣3x﹣y,
(1)求B-2A
(2)若|x﹣2a|+(y﹣3)2=0,且B﹣2A=a,求a的值.
12.已知A=2x2+3xy+2x﹣1,B=x2+xy+3x﹣2.
(1)当x=y=﹣2时,求A﹣2B的值;
(2)若A﹣2B的值与x无关,求y的值.
13.已知有理数,在数轴上的位置如图所示,化简:.
14.阅读材料:对于任何数,我们规定符号 的意义是 =ad﹣bc
例如: =1×4﹣2×3=﹣2
(1)按照这个规定,请你计算 的值.
(2)按照这个规定,请你计算当|x+y-4|+(xy+1)2=0时, 的值.
第一课时答案
一、单选题
A.C.D.A.B
二、填空题
6.﹣π2 3
7.-1.
8.5
9.1
三、解答题
10.
解:(1)
(2)
11.原式= -a2b +3ab2-a2b- 4ab2+2a2b = - ab2 .
12.
解:原式=2xy-2xy+4x2y2+6xy-10x2y2=6xy-6x2y2.
当x=,y=-3时,原式=6××(-3)-6×()2×(-3)2=-6-6=-12.
13.(1)(3x2+6x+8)﹣(6x+5x2+2)
=3x2+6x+8﹣6x﹣5x2﹣2
=﹣2x2+6;
(2)设“”是a,
则原式=(ax2+6x+8)﹣(6x+5x2+2)
=ax2+6x+8﹣6x﹣5x2﹣2
=(a﹣5)x2+6,
∵标准答案的结果是常数,
∴a﹣5=0,
解得:a=5.
14.
解:(1)装饰物的面积为:π()2=b2,窗户能射进阳光的面积是: ab-b2;
故答案为:,;
(2)ab-b2=×1-×1
=-
=
(3)更大了,
窗帘的面积:π()2=b2 ,
( ab-b2)-(ab-b2)=b2-b2=b2
∴此时窗户能射进阳光的面积更大了,大b2.
第二课时答案
一、单选题
C.D.C.C.D.
二、填空题
6.1
7.0
8.<
9.8n+6.
三、解答题
10.
(1)原式=5x2-3x-3
∵x=5,
∴原式=107
(2)原式=-3xy-2xy2+2xy-5x2y +4xy 2+5x2y
=-xy+2xy 2
由得x=-4 y=- ,
∴原式=-(-4)×(-)+2×(-4)×(-)2=-2-2=-4.
11.解:(1)、B﹣2A=4x2﹣6xy+2y2﹣3x﹣y﹣2(2x2﹣3xy+y2+2x+2y)
=4x2﹣6xy+2y2﹣3x﹣y﹣4x2+6xy﹣2y2﹣4x﹣4y=﹣7x﹣5y
(2)、∵|x﹣2a|+(y﹣3)2=0 ∴x=2a,y=3
又B﹣2A=a, ∴﹣7×2a﹣5×3=a, ∴a=﹣1.
12.A﹣2B=(2x2+3xy+2x﹣1)﹣2(x2+xy+3x﹣2)=xy﹣4x+3,
(1)当x=y=﹣2时,A﹣2B=(﹣2)×(﹣2)﹣4×(﹣2)+3=15;
(2)A﹣2B=xy﹣4x+3=(y﹣4)x+3
∵A﹣2B的值与x无关,
∴y﹣4=0,
解得:y=4.
13.
解:由数轴可知:,
∴,,,
∴原式,
,
.
故答案为.
14.
解:(1) =5×8﹣(-2)×6=52.
(2)由|x+y-4|+(xy+1)2=0得x+y-4=0,∴xy+1=0. x+y=4,∴xy=-1.
∴ =2x+1+3xy+2y=2(x+y)+3xy+1=2×4+3×(-1)+1=6.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
