沪科版七年级数学上册 4.1几何图形 同步练习(2课时 含答案)
文档属性
| 名称 | 沪科版七年级数学上册 4.1几何图形 同步练习(2课时 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 476.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 09:59:00 | ||
图片预览

文档简介
4.1几何图形
第一课时
一、选择题
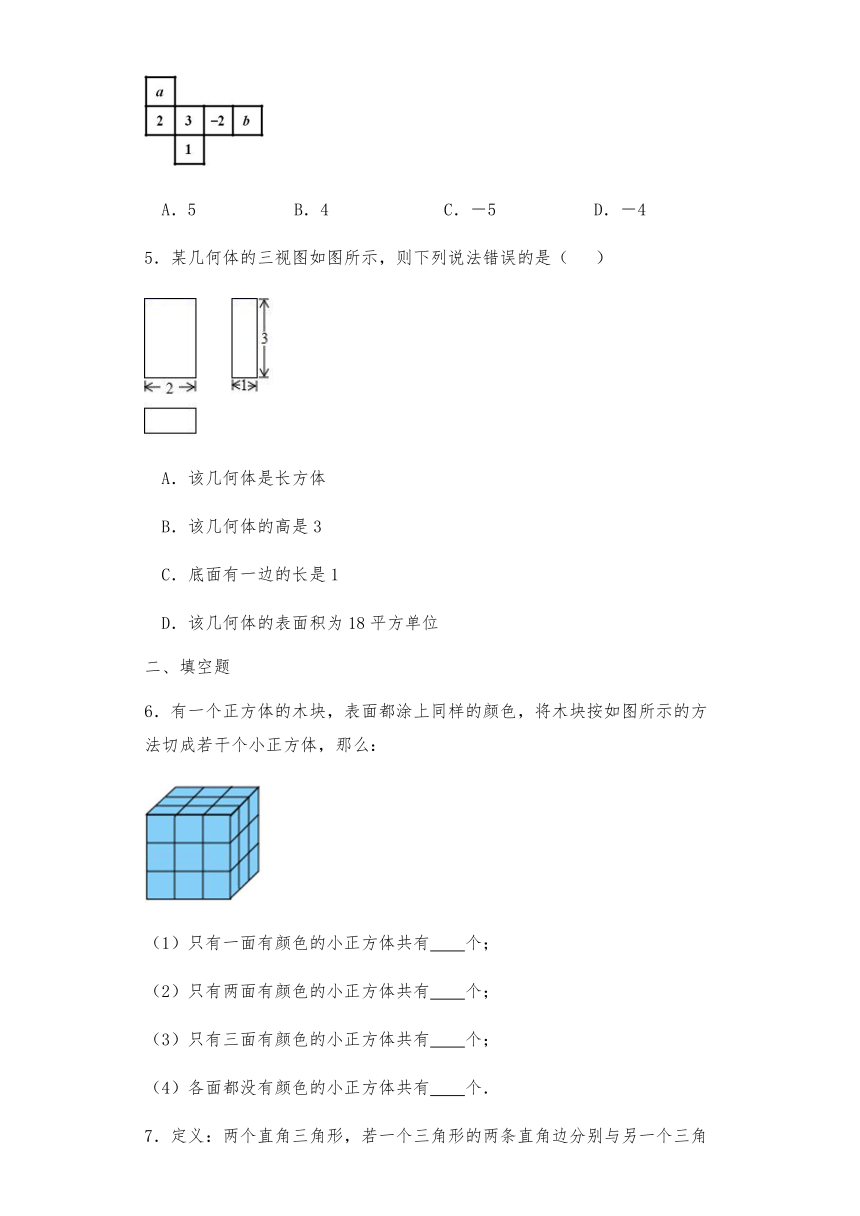
1.将下图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A. B. C. D.
2.下图中不是正方体的表面展开图的是( )
A. B.
C. D.
3.某正方体的每个面上都有一个汉字,如图是它的一中展开图,那么在原正方体中,与点字所在面相对的面上的汉字是( )
A.青 B.春 C.梦 D.想
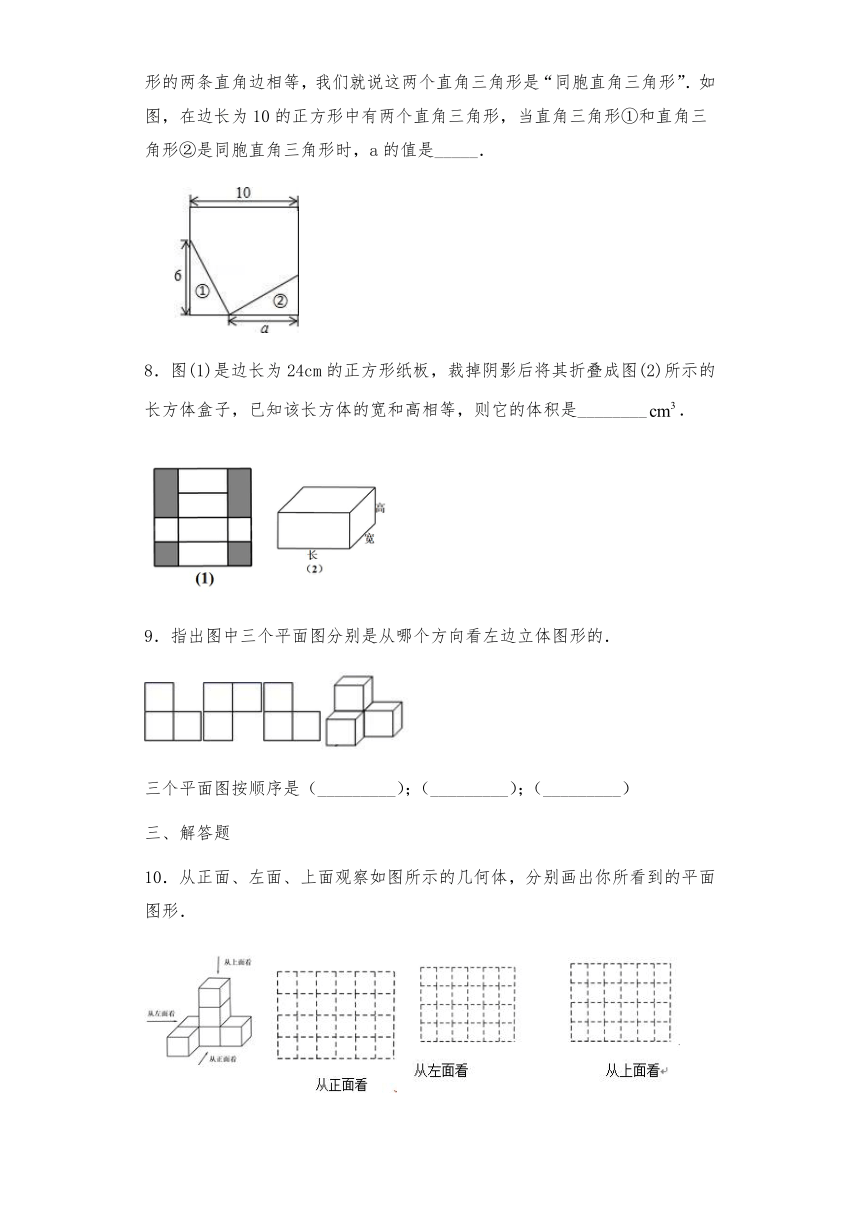
4.若如图的平面展开图折叠成正方体后,相对面上两个数都互为相反数,则a+b=( )
A.5 B.4 C.-5 D.-4
5.某几何体的三视图如图所示,则下列说法错误的是( )
A.该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是1
D.该几何体的表面积为18平方单位
二、填空题
6.有一个正方体的木块,表面都涂上同样的颜色,将木块按如图所示的方法切成若干个小正方体,那么:
(1)只有一面有颜色的小正方体共有 个;
(2)只有两面有颜色的小正方体共有 个;
(3)只有三面有颜色的小正方体共有 个;
(4)各面都没有颜色的小正方体共有 个.
7.定义:两个直角三角形,若一个三角形的两条直角边分别与另一个三角形的两条直角边相等,我们就说这两个直角三角形是“同胞直角三角形”.如图,在边长为10的正方形中有两个直角三角形,当直角三角形①和直角三角形②是同胞直角三角形时,a的值是_____.
8.图(1)是边长为24cm的正方形纸板,裁掉阴影后将其折叠成图(2)所示的长方体盒子,已知该长方体的宽和高相等,则它的体积是________.
9.指出图中三个平面图分别是从哪个方向看左边立体图形的.
三个平面图按顺序是(_________);(_________);(_________)
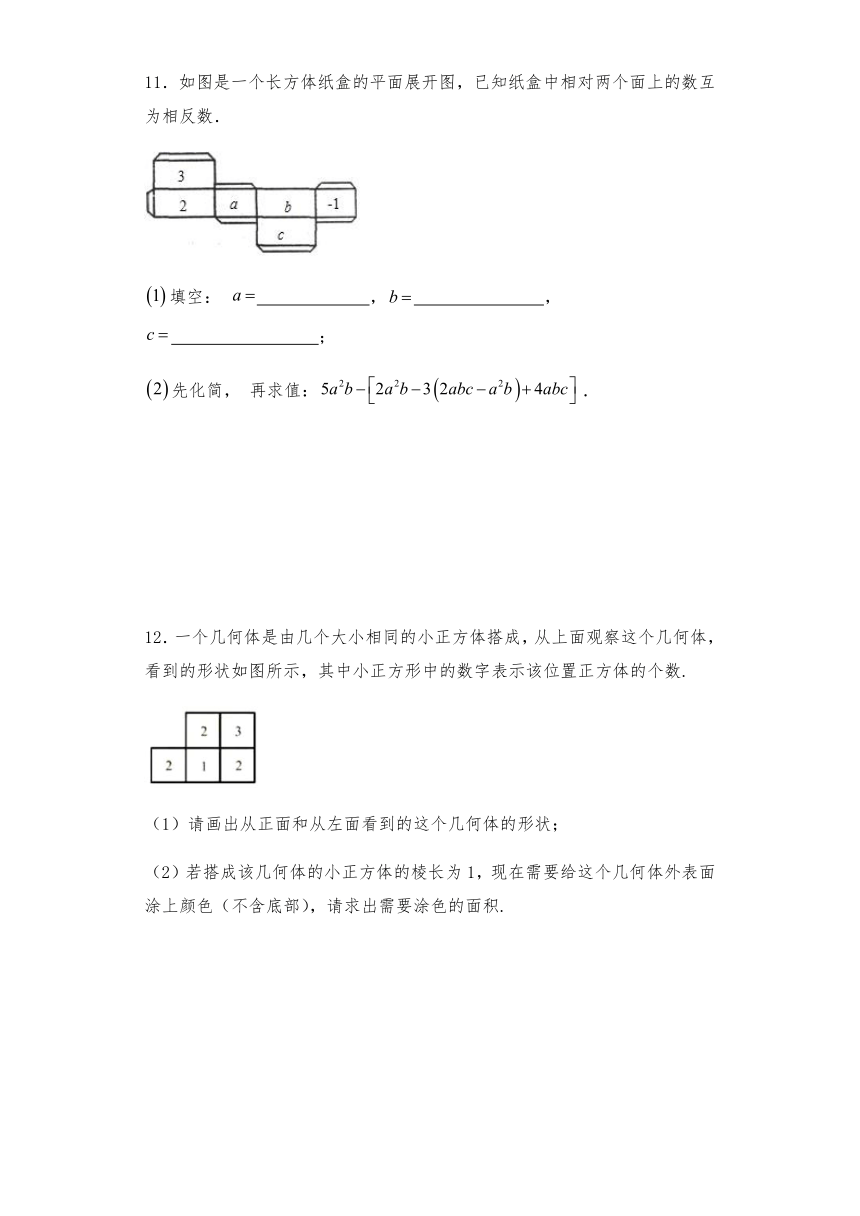
三、解答题
10.从正面、左面、上面观察如图所示的几何体,分别画出你所看到的平面图形.
11.如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
填空: , , ;
先化简, 再求值:.
12.一个几何体是由几个大小相同的小正方体搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示该位置正方体的个数.
(1)请画出从正面和从左面看到的这个几何体的形状;
(2)若搭成该几何体的小正方体的棱长为1,现在需要给这个几何体外表面涂上颜色(不含底部),请求出需要涂色的面积.
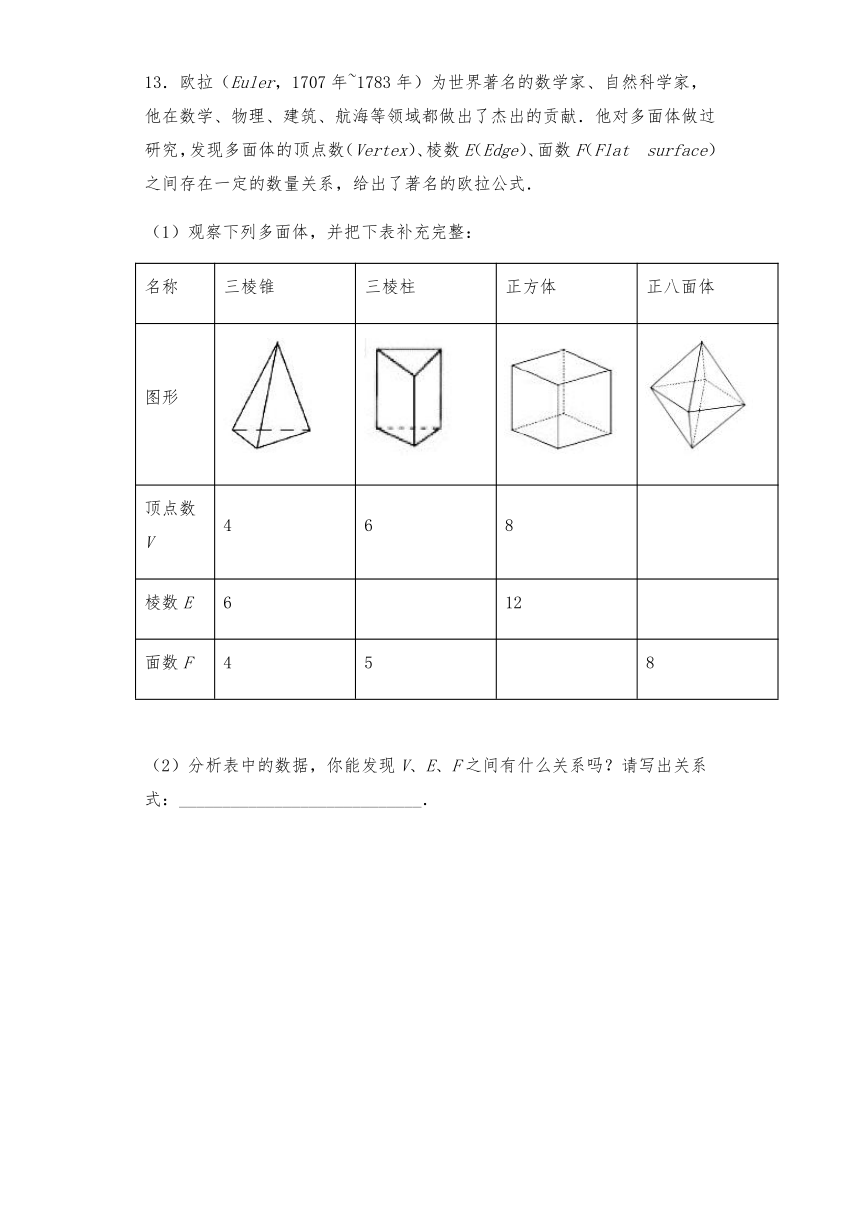
13.欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
名称 三棱锥 三棱柱 正方体 正八面体
图形
顶点数V 4 6 8
棱数E 6 12
面数F 4 5 8
(2)分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式:____________________________.
14.综合与实践
某“综合与实践”小组开展了“长方体纸盒的制作”实践活动,他们利用边长为的正方形纸板制作出两种不同方案的长方体盒子(图1为无盖的长方体纸盒,图2为有盖的长方体纸盒),请你动手操作验证并完成任务.(纸板厚度及接缝处忽略不计)
动手操作一:
根据图1方式制作一个无盖的长方体盒子.方法:先在纸板四角剪去四个同样大小边长为的小正方形,再沿虚线折合起来.
问题解决
(1)该长方体纸盒的底面边长为_______;(请你用含的代数式表示)
(2)若,,则长方体纸盒的底面积为_______;
动手操作二:
根据图2方式制作一个有盖的长方体纸盒.方法:先在纸板四角剪去两个同样大小边长为的小正方形和两个同样大小的小长方形,再沿虚线折合起来.
拓展延伸
(3)该长方体纸盒的体积为______;(请你用含的代数式表示)
(4)现有两张边长均为的正方形纸板,分别按图1、图2的要求制作无盖和有盖的两个长方体盒子,若,求无盖盒子的体积是有盖盒子体积的多少倍.
第二课时
一、选择题
1.从正面观察如图的两个立体图形,得到的平面图形是( )
A. B. C. D.
2.如图,有一个正方体纸巾盒,它的平面展开图是( )
A. B. C. D.
3.如图,含有曲面的几何体编号是( )
A.①② B.①③ C.②③ D.②④
4.如图1是一个正方体的展开图,该正方体按如图2所示的位置摆放,此时这个正方体朝下的一面的字是( )
A.中 B.国 C.梦 D.强
5.如图是某正方体的展开图,在顶点处标有数字,当把它折成正方体时,与重合的数字是( )
A.和 B.和 C.和 D.和
二、填空题
6.把一根长为分米的圆柱形木料,按锯成两段小圆柱木料后,表面积增加平方分米,较长一段木料的体积是_______立方分米.
7.如图是一个正六棱柱的主视图和左视图,则图中a的值为____.
8.乐乐发现三个大小相同的球可以恰好放在一个圆柱形盒子里(底和盖的厚度均忽略不计),如图所示,则三个球的体积之和占整个盒子容积的__________.(球的体积计算公式为)
9.如果一个物体的顶点数与面数相同,并且有八条棱,那么这个物体是_____________.
三、解答题
10.如图所示的五棱柱的底面边长都是,侧棱长,它有多少个面?它的所有侧面的面积之和是多少?
11.如图是某种产品展开图,高为3cm.
(1)求这个产品的体积.
(2)请为厂家设计一种包装纸箱,使每箱能装5件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸的厚度不计,纸箱的表面积尽可能小),求此长方体的表面积.
12.如图所示是一个正方体的表面展开图,请回答下列问题:
(1)与面B、面C相对的面分别是 和 ;
(2)若A=a3+a2b+3,B=﹣a2b+a3,C=a3﹣1,D=﹣(a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
13.把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有 小正方体?
(2)其中两面被涂到的有 个小正方体;没被涂到的有 个小正方体;
(3)求出涂上颜色部分的总面积.
14.仔细观察下面的正四面体、正六面体、正八面体,解决下列问题:
⑴填空:
①正四面体的顶点数V= ,面数F= ,棱数E= .
②正六面体的顶点数V= ,面数F= ,棱数E= .
③正八面体的顶点数V= ,面数F= ,棱数E= .
⑵若将多面体的顶点数用V表示,面数用F表示,棱数用E表示,则V、F、E之间的数量关系可用一个公式来表示,这就是著名的欧拉公式,请写出欧拉公式:
⑶如果一个多面体的棱数为30,顶点数为20,那么它有多少个面?
第一课时答案
一、选择题
C.A.B.D.D
二、填空题
6.(1);(2); (3);(4) .
7.6.
8.432
9.从正面看 从上面看 从左面看
三、解答题
10.
从正面看:共有3列,从左往右分别有1,3,1个小正方形;
从左面看:共有2列,左面一列有3个,右边一列有1个小正方形;
从上面看:共分3列,左面一列有2个,右边二列靠上方各有1个小正方形.
如图所示:
11.
解:(1)由长方体纸盒的平面展开图知,a与-1、b与2、c与3是相对的两个面上的数字或字母,
因为相对的两个面上的数互为相反数,
所以a=1,b=-2,c=-3.
故答案为:1,-2,-3.
(2)原式=5a2b﹣[2a2b﹣6abc+3a2b+4abc]
=5a2b﹣2a2b+6abc﹣3a2b﹣4abc
=5a2b﹣2a2b﹣3a2b+6abc﹣4abc
=2abc.
当a=1,b=﹣2,c=﹣3时,代入,
原式=2×1×(﹣2)×(﹣3)=12.
12.
(1)主视图有3列,每列小正方形数目分别为2,2,3,左视图有2列,每列小正方数形数目分别为3,2.
如图所示:
(2)涂上颜色部分的总面积: 2×(6+7)+5=31(平方单位).
答:涂上颜色部分的总面积是31(平方单位).
13.
解:(1)填表如下:
名称 三棱锥 三棱柱 正方体 正八面体
图形
顶点数V 4 6 8 6
棱数E 6 9 12 12
面数F 4 5 6 8
(2)据上表中的数据规律发现,多面体的顶点数V、棱数E、面数F之间存在关系式:.
14.
解:(1) 用底面大正方形的边长a减去两个小正方形的边长b
长方体纸盒的底面边长为:(a-2b)cm.
故答案为:a-2b.
(2)当 ,时,代入:
此时底面正方形的边长为:cm
故底面正方形的面积为:36cm .
故答案为:36.
(3)有盖纸盒的高即为左上角剪去的小正方形的边长,
有盖纸盒的底面为长方形,且该长方形的长为:
∵要组成一个有盖的纸盒,故如下图中A,B两块长方形的宽要一样,
∴有盖长方体纸盒底面长方形的宽为:
∴有盖长方体纸盒的体积为:
故答案为:
(4)当 时
图一中无盖长方体纸盒的体积为:,
图二中有盖长方体纸盒的体积为:.
故答案为:无盖盒子的体积是有盖盒子体积的2倍.
第二课时答案
一、选择题
A.B.C.B.D.
二、填空题
6.6
7.
8.
9.四棱锥
三、解答题
10.这个五棱柱共7个面,沿一条侧棱将其侧面全部展开成一个平面图形,这个图形是矩形,
面积为5×12×5=300cm2 .
答:这个五棱柱共7个面,侧面的面积之和是300cm2 .
11.
(1)长方体的高为3cm,则长方形的宽为(12-2×3)cm,长为(25-3-6)cm,根据题意可得:
长方形的体积为:8×6×3=144(cm3);
(2)因为长方体的高为3cm,宽为6cm,长为8cm,
所以装5件这种产品,应该尽量使得6×8的面重叠在一起,纸箱所用材料就尽可能少,
这样的话,5件这种产品可以用15×6×8的包装纸箱,再考虑15×8的面积最大,所以15×8的面重叠在一起,纸箱所用材料就尽可能少,
所以设计的包装纸箱为15×6×8规格,该产品的侧面积分别为:
8×6=48(cm2),8×15=120(cm2),6×15=90(cm2)
纸箱的表面积为:2(120+48+90)=516(cm2).
12.
(1)由“相间Z端是对面”,可得B的对面为F,C的对面是E.
故答案为:面F,面E.
(2)由题意得:A与D相对,B与F相对,C与E相对,
A+D=B+F=C+E
将A=a3a2b+3,Ba2b+a3,C=a3﹣1,D(a2b+15)代入得:
a3a2b+3(a2b+15)a2b+a3+F=a3﹣1+E,
∴Fa2b,
E=1.
13.
(1)该几何体中正方体的个数为9+4+1=14个;
(2)根据图中小正方体的位置可知:最底层外边中间的小正方体被涂到2个面,共4个,只有最底层正中间的小正方体没被涂到,
故答案为4;1;
(3)先算侧面--底层12个小面; 中层8个小面; 上层4个小面;
再算上面--上层1个 中层3个(正方体是可以移动的,不管放在哪里,它压住的面积总是它的底面积,也就是一个,所以中层是4减1个)底层(9-4)=5个,
∴总共12+8+4+1+3+5=33个小面.
∴涂上颜色部分的总面积=1133=33cm2.
14.
解:⑴①4,4,6;②8,6,12;③6,8,12;
⑵V+F-E=2
⑶解:设面数为F,则20+F-30=2 解得F=12
答:它有12个面.
第一课时
一、选择题
1.将下图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A. B. C. D.
2.下图中不是正方体的表面展开图的是( )
A. B.
C. D.
3.某正方体的每个面上都有一个汉字,如图是它的一中展开图,那么在原正方体中,与点字所在面相对的面上的汉字是( )
A.青 B.春 C.梦 D.想
4.若如图的平面展开图折叠成正方体后,相对面上两个数都互为相反数,则a+b=( )
A.5 B.4 C.-5 D.-4
5.某几何体的三视图如图所示,则下列说法错误的是( )
A.该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是1
D.该几何体的表面积为18平方单位
二、填空题
6.有一个正方体的木块,表面都涂上同样的颜色,将木块按如图所示的方法切成若干个小正方体,那么:
(1)只有一面有颜色的小正方体共有 个;
(2)只有两面有颜色的小正方体共有 个;
(3)只有三面有颜色的小正方体共有 个;
(4)各面都没有颜色的小正方体共有 个.
7.定义:两个直角三角形,若一个三角形的两条直角边分别与另一个三角形的两条直角边相等,我们就说这两个直角三角形是“同胞直角三角形”.如图,在边长为10的正方形中有两个直角三角形,当直角三角形①和直角三角形②是同胞直角三角形时,a的值是_____.
8.图(1)是边长为24cm的正方形纸板,裁掉阴影后将其折叠成图(2)所示的长方体盒子,已知该长方体的宽和高相等,则它的体积是________.
9.指出图中三个平面图分别是从哪个方向看左边立体图形的.
三个平面图按顺序是(_________);(_________);(_________)
三、解答题
10.从正面、左面、上面观察如图所示的几何体,分别画出你所看到的平面图形.
11.如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
填空: , , ;
先化简, 再求值:.
12.一个几何体是由几个大小相同的小正方体搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示该位置正方体的个数.
(1)请画出从正面和从左面看到的这个几何体的形状;
(2)若搭成该几何体的小正方体的棱长为1,现在需要给这个几何体外表面涂上颜色(不含底部),请求出需要涂色的面积.
13.欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
名称 三棱锥 三棱柱 正方体 正八面体
图形
顶点数V 4 6 8
棱数E 6 12
面数F 4 5 8
(2)分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式:____________________________.
14.综合与实践
某“综合与实践”小组开展了“长方体纸盒的制作”实践活动,他们利用边长为的正方形纸板制作出两种不同方案的长方体盒子(图1为无盖的长方体纸盒,图2为有盖的长方体纸盒),请你动手操作验证并完成任务.(纸板厚度及接缝处忽略不计)
动手操作一:
根据图1方式制作一个无盖的长方体盒子.方法:先在纸板四角剪去四个同样大小边长为的小正方形,再沿虚线折合起来.
问题解决
(1)该长方体纸盒的底面边长为_______;(请你用含的代数式表示)
(2)若,,则长方体纸盒的底面积为_______;
动手操作二:
根据图2方式制作一个有盖的长方体纸盒.方法:先在纸板四角剪去两个同样大小边长为的小正方形和两个同样大小的小长方形,再沿虚线折合起来.
拓展延伸
(3)该长方体纸盒的体积为______;(请你用含的代数式表示)
(4)现有两张边长均为的正方形纸板,分别按图1、图2的要求制作无盖和有盖的两个长方体盒子,若,求无盖盒子的体积是有盖盒子体积的多少倍.
第二课时
一、选择题
1.从正面观察如图的两个立体图形,得到的平面图形是( )
A. B. C. D.
2.如图,有一个正方体纸巾盒,它的平面展开图是( )
A. B. C. D.
3.如图,含有曲面的几何体编号是( )
A.①② B.①③ C.②③ D.②④
4.如图1是一个正方体的展开图,该正方体按如图2所示的位置摆放,此时这个正方体朝下的一面的字是( )
A.中 B.国 C.梦 D.强
5.如图是某正方体的展开图,在顶点处标有数字,当把它折成正方体时,与重合的数字是( )
A.和 B.和 C.和 D.和
二、填空题
6.把一根长为分米的圆柱形木料,按锯成两段小圆柱木料后,表面积增加平方分米,较长一段木料的体积是_______立方分米.
7.如图是一个正六棱柱的主视图和左视图,则图中a的值为____.
8.乐乐发现三个大小相同的球可以恰好放在一个圆柱形盒子里(底和盖的厚度均忽略不计),如图所示,则三个球的体积之和占整个盒子容积的__________.(球的体积计算公式为)
9.如果一个物体的顶点数与面数相同,并且有八条棱,那么这个物体是_____________.
三、解答题
10.如图所示的五棱柱的底面边长都是,侧棱长,它有多少个面?它的所有侧面的面积之和是多少?
11.如图是某种产品展开图,高为3cm.
(1)求这个产品的体积.
(2)请为厂家设计一种包装纸箱,使每箱能装5件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸的厚度不计,纸箱的表面积尽可能小),求此长方体的表面积.
12.如图所示是一个正方体的表面展开图,请回答下列问题:
(1)与面B、面C相对的面分别是 和 ;
(2)若A=a3+a2b+3,B=﹣a2b+a3,C=a3﹣1,D=﹣(a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
13.把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有 小正方体?
(2)其中两面被涂到的有 个小正方体;没被涂到的有 个小正方体;
(3)求出涂上颜色部分的总面积.
14.仔细观察下面的正四面体、正六面体、正八面体,解决下列问题:
⑴填空:
①正四面体的顶点数V= ,面数F= ,棱数E= .
②正六面体的顶点数V= ,面数F= ,棱数E= .
③正八面体的顶点数V= ,面数F= ,棱数E= .
⑵若将多面体的顶点数用V表示,面数用F表示,棱数用E表示,则V、F、E之间的数量关系可用一个公式来表示,这就是著名的欧拉公式,请写出欧拉公式:
⑶如果一个多面体的棱数为30,顶点数为20,那么它有多少个面?
第一课时答案
一、选择题
C.A.B.D.D
二、填空题
6.(1);(2); (3);(4) .
7.6.
8.432
9.从正面看 从上面看 从左面看
三、解答题
10.
从正面看:共有3列,从左往右分别有1,3,1个小正方形;
从左面看:共有2列,左面一列有3个,右边一列有1个小正方形;
从上面看:共分3列,左面一列有2个,右边二列靠上方各有1个小正方形.
如图所示:
11.
解:(1)由长方体纸盒的平面展开图知,a与-1、b与2、c与3是相对的两个面上的数字或字母,
因为相对的两个面上的数互为相反数,
所以a=1,b=-2,c=-3.
故答案为:1,-2,-3.
(2)原式=5a2b﹣[2a2b﹣6abc+3a2b+4abc]
=5a2b﹣2a2b+6abc﹣3a2b﹣4abc
=5a2b﹣2a2b﹣3a2b+6abc﹣4abc
=2abc.
当a=1,b=﹣2,c=﹣3时,代入,
原式=2×1×(﹣2)×(﹣3)=12.
12.
(1)主视图有3列,每列小正方形数目分别为2,2,3,左视图有2列,每列小正方数形数目分别为3,2.
如图所示:
(2)涂上颜色部分的总面积: 2×(6+7)+5=31(平方单位).
答:涂上颜色部分的总面积是31(平方单位).
13.
解:(1)填表如下:
名称 三棱锥 三棱柱 正方体 正八面体
图形
顶点数V 4 6 8 6
棱数E 6 9 12 12
面数F 4 5 6 8
(2)据上表中的数据规律发现,多面体的顶点数V、棱数E、面数F之间存在关系式:.
14.
解:(1) 用底面大正方形的边长a减去两个小正方形的边长b
长方体纸盒的底面边长为:(a-2b)cm.
故答案为:a-2b.
(2)当 ,时,代入:
此时底面正方形的边长为:cm
故底面正方形的面积为:36cm .
故答案为:36.
(3)有盖纸盒的高即为左上角剪去的小正方形的边长,
有盖纸盒的底面为长方形,且该长方形的长为:
∵要组成一个有盖的纸盒,故如下图中A,B两块长方形的宽要一样,
∴有盖长方体纸盒底面长方形的宽为:
∴有盖长方体纸盒的体积为:
故答案为:
(4)当 时
图一中无盖长方体纸盒的体积为:,
图二中有盖长方体纸盒的体积为:.
故答案为:无盖盒子的体积是有盖盒子体积的2倍.
第二课时答案
一、选择题
A.B.C.B.D.
二、填空题
6.6
7.
8.
9.四棱锥
三、解答题
10.这个五棱柱共7个面,沿一条侧棱将其侧面全部展开成一个平面图形,这个图形是矩形,
面积为5×12×5=300cm2 .
答:这个五棱柱共7个面,侧面的面积之和是300cm2 .
11.
(1)长方体的高为3cm,则长方形的宽为(12-2×3)cm,长为(25-3-6)cm,根据题意可得:
长方形的体积为:8×6×3=144(cm3);
(2)因为长方体的高为3cm,宽为6cm,长为8cm,
所以装5件这种产品,应该尽量使得6×8的面重叠在一起,纸箱所用材料就尽可能少,
这样的话,5件这种产品可以用15×6×8的包装纸箱,再考虑15×8的面积最大,所以15×8的面重叠在一起,纸箱所用材料就尽可能少,
所以设计的包装纸箱为15×6×8规格,该产品的侧面积分别为:
8×6=48(cm2),8×15=120(cm2),6×15=90(cm2)
纸箱的表面积为:2(120+48+90)=516(cm2).
12.
(1)由“相间Z端是对面”,可得B的对面为F,C的对面是E.
故答案为:面F,面E.
(2)由题意得:A与D相对,B与F相对,C与E相对,
A+D=B+F=C+E
将A=a3a2b+3,Ba2b+a3,C=a3﹣1,D(a2b+15)代入得:
a3a2b+3(a2b+15)a2b+a3+F=a3﹣1+E,
∴Fa2b,
E=1.
13.
(1)该几何体中正方体的个数为9+4+1=14个;
(2)根据图中小正方体的位置可知:最底层外边中间的小正方体被涂到2个面,共4个,只有最底层正中间的小正方体没被涂到,
故答案为4;1;
(3)先算侧面--底层12个小面; 中层8个小面; 上层4个小面;
再算上面--上层1个 中层3个(正方体是可以移动的,不管放在哪里,它压住的面积总是它的底面积,也就是一个,所以中层是4减1个)底层(9-4)=5个,
∴总共12+8+4+1+3+5=33个小面.
∴涂上颜色部分的总面积=1133=33cm2.
14.
解:⑴①4,4,6;②8,6,12;③6,8,12;
⑵V+F-E=2
⑶解:设面数为F,则20+F-30=2 解得F=12
答:它有12个面.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
