沪科版七年级数学上册 4.2线段、射线、直线 同步练习(2课时 含答案)
文档属性
| 名称 | 沪科版七年级数学上册 4.2线段、射线、直线 同步练习(2课时 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 360.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 00:00:00 | ||
图片预览



文档简介
4.2线段、射线、直线
第一课时
一、选择题
1.下列说法错误的是( )
A.直线l经过点A
B.直线a,b相交于点A
C.点C在线段AB上
D.射线CD与线段AB有公共点
2.下列各图中所给的线段、射线、直线能相交的是( )
A. B. C. D.
3.如图,下列关系式中与图不符合的式子是( )
A.AD﹣CD=AB+BC B.AC﹣BC=AD﹣BD
C.AC﹣BC=AC+BD D.AD﹣AC=BD﹣BC
4.已知点A,B,C是一条直线上的三点,若AB=5,BC=3则AC长为( )
A.8 B.2 C.8或2 D.无法确定
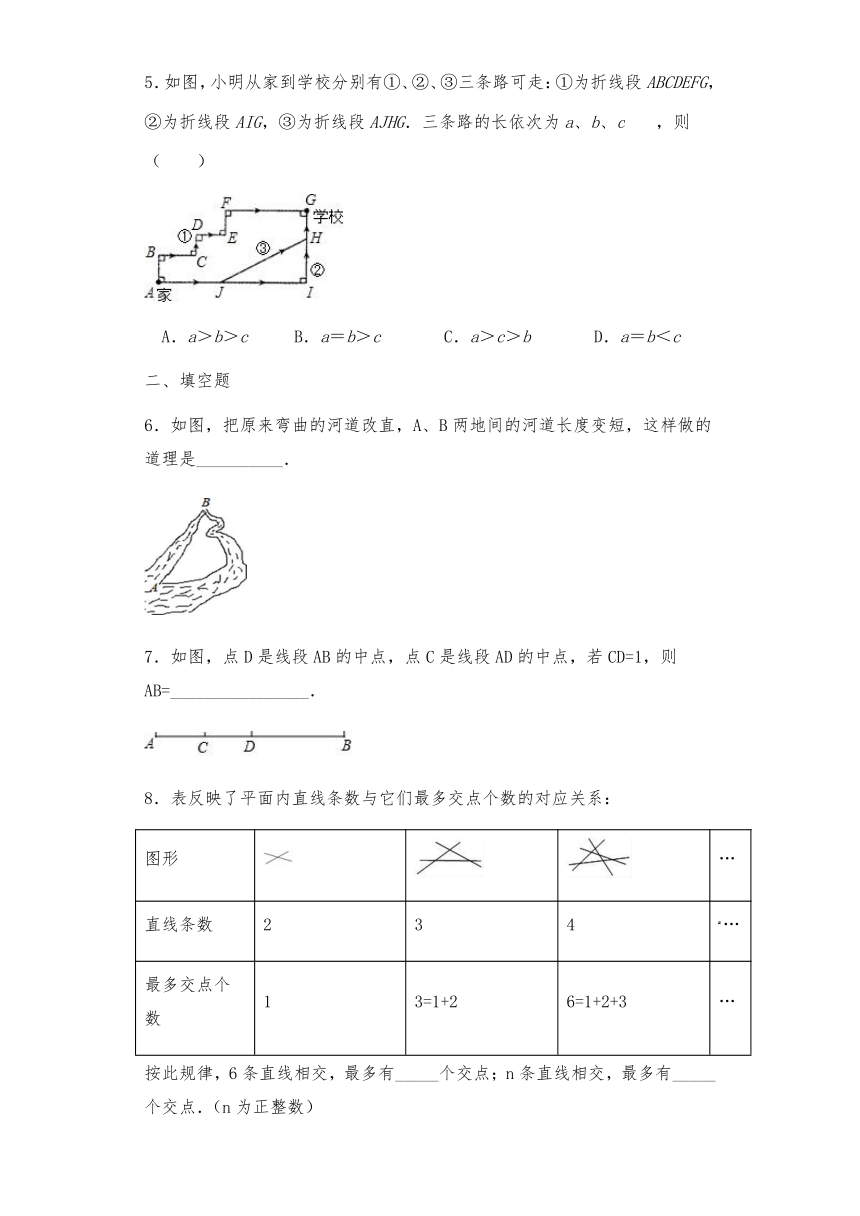
5.如图,小明从家到学校分别有①、②、③三条路可走:①为折线段ABCDEFG,②为折线段AIG,③为折线段AJHG.三条路的长依次为a、b、c,则( )
A.a>b>c B.a=b>c C.a>c>b D.a=b<c
二、填空题
6.如图,把原来弯曲的河道改直,A、B两地间的河道长度变短,这样做的道理是__________.
7.如图,点D是线段AB的中点,点C是线段AD的中点,若CD=1,则AB=________________.
8.表反映了平面内直线条数与它们最多交点个数的对应关系:
图形 …
直线条数 2 3 4 …
最多交点个数 1 3=1+2 6=1+2+3 …
按此规律,6条直线相交,最多有_____个交点;n条直线相交,最多有_____个交点.(n为正整数)
9.如图,该图中不同的线段共有____条.
三、解答题
10.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近?画图并说明理由;
(2)从码头到铁路怎样走最近?画图并说明理由;
(3)从火车站到河流怎样走最近?画图并说明理由.
11.如图,已知平面上有四个点A,B,C,D.
(1)连接AB,并画出AB的中点P;
(2)作射线AD;
(3)作直线BC与射线AD交于点E.
12.已知,满足等式.
(1)求,的值;
(2)已知线段,在直线上取一点,恰好使,点为的中点,求线段的长.
13.如图,M是线段AB的中点,点C在线段AB上,且AC=8cm,N是AC的中点,MN=6cm,求线段CM和AB的长.
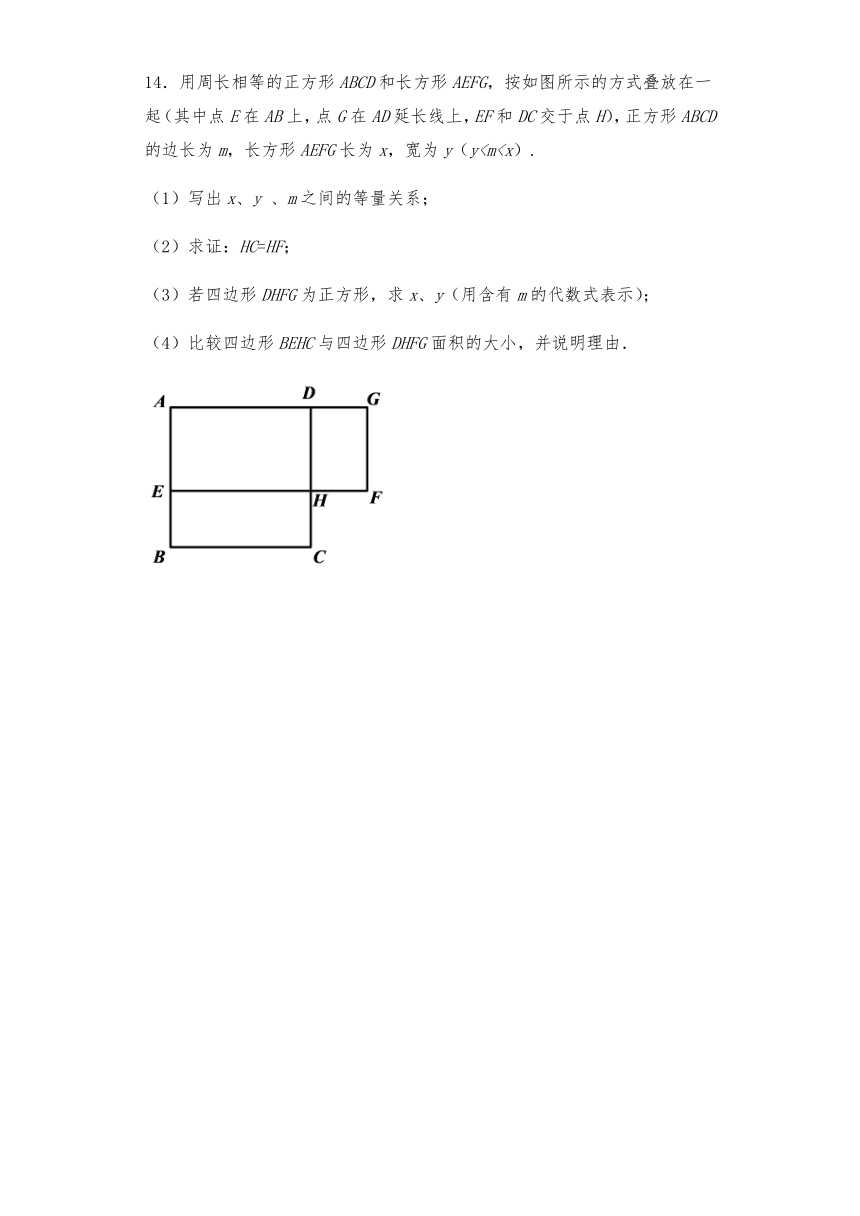
14.用周长相等的正方形ABCD和长方形AEFG,按如图所示的方式叠放在一起(其中点E在AB上,点G在AD延长线上,EF和DC交于点H),正方形ABCD的边长为m,长方形AEFG长为x,宽为y(y(1)写出x、y 、m之间的等量关系;
(2)求证:HC=HF;
(3)若四边形DHFG为正方形,求x、y(用含有m的代数式表示);
(4)比较四边形BEHC与四边形DHFG面积的大小,并说明理由.
第二课时
一、选择题
1.两条相交直线与另外一条直线在同一平面内,它们的交点个数是( ).
A.1 B.2 C.1或2或3 D.0或1或2或3
2.在平面上有任意四个点,那么这四个点可以确定的直线有( )
A.1条 B.4条 C.6条 D.1条或4条或6条
3.已知线段AB=10cm,在直线AB上取一点C,使AC=16cm,则线段AB的中点与AC的中点的距离为( )
A.13cm或26cm B.6cm或13cm C.6cm或25cm D.3cm或13cm
4.平面内两两相交的6条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.12 B.16 C.20 D.以上都不对
5.图中有4根绳子,在绳的两端用力拉,有一根绳子是能打成结的,请问是哪一根?( ).
A. B. C. D.
二、填空题
6.往返于临江、靖宇两地的客车中途停靠3个站,最多有______种不同的票价.
7.木工师傅在锯木料时,一般先在木料上画出两个点,然后过这两个点弹出一条墨线,这是因为_________________.
8.点A,B,C在同一条直线上,AB=1cm,BC=3AB,则AC的长为_________.
9.如图,从点O引出的射线(任两条不共线)条数与角的总个数有如下关系:从点O引出两条射线形成1个角;如图1从点O引出3条射线共形成3个角;如图2从点O引出4条射线共形成6个角;如图3从点O引出5条射线共形成10个角;
(1)观察操作:当从点O引出6条射线共形成有________个角;
(2)探索发现:如图4当从点O引出n条射线共形成________个角;(用含n的式子表示)
(3)实践应用:8支篮球队进行单循环比赛(参加比赛的每两支球队之间都要进行一场比赛),总的比赛场数为__________场.如果n支篮球队进行主客场制单循环赛(参加的每个队都与其它所有队各赛2场)总的比赛场数是______场.
三、解答题
10.如图,在数轴上有A,B两点,点A在点B的左侧.已知点B对应的数为2,点A对应的数为a.
(1)若a=﹣1,则线段AB的长为 ;
(2)若点C到原点的距离为3,且在点A的左侧,BC﹣AC=4,求a的值.
11.如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
(1)写出数轴上点B所表示的数 ;
(2)点P所表示的数 ;(用含t的代数式表示);
(3)M是AP的中点,N为PB的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,说明理由;若不变,请你画出图形,并求出线段MN的长.
12.作图题:如图,已知四点A、B、C、D,按照下列语句画图:
(1)画射线BC;
(2)画线段AC、BD相交于点F;
(3)画直线AB、CD相交于点E.
13.已知数轴上两点所表示的数分别为和,且满足,为原点.
(1)试求和的值;
(2)点从点出发向右运动,经过3秒后点到点的距离是点到点距离的3倍,求点的运动速度?
(3)点以一个单位每秒的速度从点向右运动,同时点从点出发以5个单位每秒的速度向左运动,点从点出发,以20个单位每秒的速度向右运动.在运动过程中,分别为的中点,问的值是否发生变化,请说明理由.
14.已知:如图1,M是定长线段AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上)
(1)若AB=10cm,当点C、D运动了2s,求AC+MD的值.
(2)若点C、D运动时,总有MD=3AC,直接填空:AM= AB.
(3)在(2)的条件下,N是直线AB上一点,且AN-BN=MN,求的值.
第一课时答案
一、选择题
C.B.C.C.B.
二、填空题
6.两点之间,线段最短
7.4
8.15,
9.10
三、解答题
10.
解:如图所示:
(1)沿AB走,两点之间线段最短;
(2)沿BD走,垂线段最短;
(3)沿AC走,垂线段最短.
11.
解:(1)(2)(3)由题意可得,如图所示.
12.
(1)由,得:
,,
解得:,;
(2)由(1)得,,
有两种情况:
①当点P在点B的左侧时,如图1,
∵AB=AP+PB=8,,
∴4PB=8,
解得:PB=2,
∴,
∵点Q为PB的中点,
∴,
∴AQ=AP+PQ=6+1=7;
②当点P在点B的右侧时,如图2,
∵AP=AB+BP,,
∴3PB=8+PB,
∴PB=4,
∵点Q为PB的中点,
∴,
∴AQ=AB+BQ=8+2=10.
综上,AQ的值为7或10.
13.AC=8cm,N是AC的中点
MN=6cm
14.
解:(1)∵正方形ABCD和长方形AEFG周长相等,
∴,即;
(2)∵,,
∴;
(3)∵四边形DHFG为正方形,
∴,即,
解得,
∴;
(4),,
∵,
∴,
即.
第二课时答案
一、选择题
C.D.D.B.B.
二、填空题
6.10
7.两点确定一条直线.
8.2cm或4cm
9.15 28 n(n-1)
三、解答题
10.
(1)AB=2﹣a=2﹣(﹣1)=3,
故答案为:3;
(2)∵点C到原点的距离为3,
∴设点C表示的数为c,则|c|=3,即c=±3,
∵点A在点B的左侧,点C在点A的左侧,且点B表示的数为2,
∴点C表示的数为﹣3,
∵BC﹣AC=4,
∴2﹣(﹣3)﹣[a﹣(﹣3)]=4,
解得a=﹣2.
11.(1)∵数轴上点A表示的数为6,
∴OA=6,
则OB=AB-OA=4,
点B在原点左边,
所以数轴上点B所表示的数为-4,
故答案为:-4;
(2)点P运动t秒的长度为6t,
∵动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,
∴P所表示的数为:6-6t,
故答案为:6-6t;
(3)线段MN的长度不发生变化,
理由:
分两种情况:
①当点P在A、B两点之间运动时,如图
.
②当点P运动到B的左边时,如图
综上所述,线段MN的长度不发生变化,其值为5.
12.
解:(1)如图,射线BC为所求;
(2)如图,线段AC、BD相交于点F为所求;
(3)如图,直线AB、CD相交于点E为所求.
13.解:(1)∵|a+3|+(b-9)2020=0,
∴a+3=0且b-9=0,
∴a=-3,b=9;
(2)设点运动的速度为v个单位/秒,则3s后点表示的数为3v,
又由(1)知,点A表示的数为-3,点B表示的数为9,
∴,
当点C在点B左侧时,BC=9-3v,则,解得v=2;
当点C在点B右侧时,BC=3v-9,则,解得v=5,
故点C的运动速度为2个单位/秒或5个单位/秒;
(3)的值不发生变化,理由如下:
设运动的时间为,则表示的数为,表示的数为,表示的数为,
又、分别为、的中点,
∴表示的数为,表示的数为,
∴.
即的值不发生变化,其值为2.
14.
(1)当点C、D运动了2s时,
∵
∴;
(2)由运动速度可知,
故;
(3)如图,当点N在线段AB上时
∵,
即
如图,当点N在线段AB的延长线上时
∵,
∴
即
综上,的值为或1.
第一课时
一、选择题
1.下列说法错误的是( )
A.直线l经过点A
B.直线a,b相交于点A
C.点C在线段AB上
D.射线CD与线段AB有公共点
2.下列各图中所给的线段、射线、直线能相交的是( )
A. B. C. D.
3.如图,下列关系式中与图不符合的式子是( )
A.AD﹣CD=AB+BC B.AC﹣BC=AD﹣BD
C.AC﹣BC=AC+BD D.AD﹣AC=BD﹣BC
4.已知点A,B,C是一条直线上的三点,若AB=5,BC=3则AC长为( )
A.8 B.2 C.8或2 D.无法确定
5.如图,小明从家到学校分别有①、②、③三条路可走:①为折线段ABCDEFG,②为折线段AIG,③为折线段AJHG.三条路的长依次为a、b、c,则( )
A.a>b>c B.a=b>c C.a>c>b D.a=b<c
二、填空题
6.如图,把原来弯曲的河道改直,A、B两地间的河道长度变短,这样做的道理是__________.
7.如图,点D是线段AB的中点,点C是线段AD的中点,若CD=1,则AB=________________.
8.表反映了平面内直线条数与它们最多交点个数的对应关系:
图形 …
直线条数 2 3 4 …
最多交点个数 1 3=1+2 6=1+2+3 …
按此规律,6条直线相交,最多有_____个交点;n条直线相交,最多有_____个交点.(n为正整数)
9.如图,该图中不同的线段共有____条.
三、解答题
10.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近?画图并说明理由;
(2)从码头到铁路怎样走最近?画图并说明理由;
(3)从火车站到河流怎样走最近?画图并说明理由.
11.如图,已知平面上有四个点A,B,C,D.
(1)连接AB,并画出AB的中点P;
(2)作射线AD;
(3)作直线BC与射线AD交于点E.
12.已知,满足等式.
(1)求,的值;
(2)已知线段,在直线上取一点,恰好使,点为的中点,求线段的长.
13.如图,M是线段AB的中点,点C在线段AB上,且AC=8cm,N是AC的中点,MN=6cm,求线段CM和AB的长.
14.用周长相等的正方形ABCD和长方形AEFG,按如图所示的方式叠放在一起(其中点E在AB上,点G在AD延长线上,EF和DC交于点H),正方形ABCD的边长为m,长方形AEFG长为x,宽为y(y
(2)求证:HC=HF;
(3)若四边形DHFG为正方形,求x、y(用含有m的代数式表示);
(4)比较四边形BEHC与四边形DHFG面积的大小,并说明理由.
第二课时
一、选择题
1.两条相交直线与另外一条直线在同一平面内,它们的交点个数是( ).
A.1 B.2 C.1或2或3 D.0或1或2或3
2.在平面上有任意四个点,那么这四个点可以确定的直线有( )
A.1条 B.4条 C.6条 D.1条或4条或6条
3.已知线段AB=10cm,在直线AB上取一点C,使AC=16cm,则线段AB的中点与AC的中点的距离为( )
A.13cm或26cm B.6cm或13cm C.6cm或25cm D.3cm或13cm
4.平面内两两相交的6条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.12 B.16 C.20 D.以上都不对
5.图中有4根绳子,在绳的两端用力拉,有一根绳子是能打成结的,请问是哪一根?( ).
A. B. C. D.
二、填空题
6.往返于临江、靖宇两地的客车中途停靠3个站,最多有______种不同的票价.
7.木工师傅在锯木料时,一般先在木料上画出两个点,然后过这两个点弹出一条墨线,这是因为_________________.
8.点A,B,C在同一条直线上,AB=1cm,BC=3AB,则AC的长为_________.
9.如图,从点O引出的射线(任两条不共线)条数与角的总个数有如下关系:从点O引出两条射线形成1个角;如图1从点O引出3条射线共形成3个角;如图2从点O引出4条射线共形成6个角;如图3从点O引出5条射线共形成10个角;
(1)观察操作:当从点O引出6条射线共形成有________个角;
(2)探索发现:如图4当从点O引出n条射线共形成________个角;(用含n的式子表示)
(3)实践应用:8支篮球队进行单循环比赛(参加比赛的每两支球队之间都要进行一场比赛),总的比赛场数为__________场.如果n支篮球队进行主客场制单循环赛(参加的每个队都与其它所有队各赛2场)总的比赛场数是______场.
三、解答题
10.如图,在数轴上有A,B两点,点A在点B的左侧.已知点B对应的数为2,点A对应的数为a.
(1)若a=﹣1,则线段AB的长为 ;
(2)若点C到原点的距离为3,且在点A的左侧,BC﹣AC=4,求a的值.
11.如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
(1)写出数轴上点B所表示的数 ;
(2)点P所表示的数 ;(用含t的代数式表示);
(3)M是AP的中点,N为PB的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,说明理由;若不变,请你画出图形,并求出线段MN的长.
12.作图题:如图,已知四点A、B、C、D,按照下列语句画图:
(1)画射线BC;
(2)画线段AC、BD相交于点F;
(3)画直线AB、CD相交于点E.
13.已知数轴上两点所表示的数分别为和,且满足,为原点.
(1)试求和的值;
(2)点从点出发向右运动,经过3秒后点到点的距离是点到点距离的3倍,求点的运动速度?
(3)点以一个单位每秒的速度从点向右运动,同时点从点出发以5个单位每秒的速度向左运动,点从点出发,以20个单位每秒的速度向右运动.在运动过程中,分别为的中点,问的值是否发生变化,请说明理由.
14.已知:如图1,M是定长线段AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上)
(1)若AB=10cm,当点C、D运动了2s,求AC+MD的值.
(2)若点C、D运动时,总有MD=3AC,直接填空:AM= AB.
(3)在(2)的条件下,N是直线AB上一点,且AN-BN=MN,求的值.
第一课时答案
一、选择题
C.B.C.C.B.
二、填空题
6.两点之间,线段最短
7.4
8.15,
9.10
三、解答题
10.
解:如图所示:
(1)沿AB走,两点之间线段最短;
(2)沿BD走,垂线段最短;
(3)沿AC走,垂线段最短.
11.
解:(1)(2)(3)由题意可得,如图所示.
12.
(1)由,得:
,,
解得:,;
(2)由(1)得,,
有两种情况:
①当点P在点B的左侧时,如图1,
∵AB=AP+PB=8,,
∴4PB=8,
解得:PB=2,
∴,
∵点Q为PB的中点,
∴,
∴AQ=AP+PQ=6+1=7;
②当点P在点B的右侧时,如图2,
∵AP=AB+BP,,
∴3PB=8+PB,
∴PB=4,
∵点Q为PB的中点,
∴,
∴AQ=AB+BQ=8+2=10.
综上,AQ的值为7或10.
13.AC=8cm,N是AC的中点
MN=6cm
14.
解:(1)∵正方形ABCD和长方形AEFG周长相等,
∴,即;
(2)∵,,
∴;
(3)∵四边形DHFG为正方形,
∴,即,
解得,
∴;
(4),,
∵,
∴,
即.
第二课时答案
一、选择题
C.D.D.B.B.
二、填空题
6.10
7.两点确定一条直线.
8.2cm或4cm
9.15 28 n(n-1)
三、解答题
10.
(1)AB=2﹣a=2﹣(﹣1)=3,
故答案为:3;
(2)∵点C到原点的距离为3,
∴设点C表示的数为c,则|c|=3,即c=±3,
∵点A在点B的左侧,点C在点A的左侧,且点B表示的数为2,
∴点C表示的数为﹣3,
∵BC﹣AC=4,
∴2﹣(﹣3)﹣[a﹣(﹣3)]=4,
解得a=﹣2.
11.(1)∵数轴上点A表示的数为6,
∴OA=6,
则OB=AB-OA=4,
点B在原点左边,
所以数轴上点B所表示的数为-4,
故答案为:-4;
(2)点P运动t秒的长度为6t,
∵动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,
∴P所表示的数为:6-6t,
故答案为:6-6t;
(3)线段MN的长度不发生变化,
理由:
分两种情况:
①当点P在A、B两点之间运动时,如图
.
②当点P运动到B的左边时,如图
综上所述,线段MN的长度不发生变化,其值为5.
12.
解:(1)如图,射线BC为所求;
(2)如图,线段AC、BD相交于点F为所求;
(3)如图,直线AB、CD相交于点E为所求.
13.解:(1)∵|a+3|+(b-9)2020=0,
∴a+3=0且b-9=0,
∴a=-3,b=9;
(2)设点运动的速度为v个单位/秒,则3s后点表示的数为3v,
又由(1)知,点A表示的数为-3,点B表示的数为9,
∴,
当点C在点B左侧时,BC=9-3v,则,解得v=2;
当点C在点B右侧时,BC=3v-9,则,解得v=5,
故点C的运动速度为2个单位/秒或5个单位/秒;
(3)的值不发生变化,理由如下:
设运动的时间为,则表示的数为,表示的数为,表示的数为,
又、分别为、的中点,
∴表示的数为,表示的数为,
∴.
即的值不发生变化,其值为2.
14.
(1)当点C、D运动了2s时,
∵
∴;
(2)由运动速度可知,
故;
(3)如图,当点N在线段AB上时
∵,
即
如图,当点N在线段AB的延长线上时
∵,
∴
即
综上,的值为或1.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
