九年级数学上册试题 22.2相似三角形的判定同步练习沪科版(含答案)
文档属性
| 名称 | 九年级数学上册试题 22.2相似三角形的判定同步练习沪科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 517.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 14:40:19 | ||
图片预览




文档简介
22.2相似三角形的判定
第一课时
一、单选题
1.在△ABC中,三条边的长分别为2、3、4,△A′B′C′的两边长分别为1、1.5,要使△ABC∽△A′B′C′,那么△A′B′C′的第三边长应该是( )
A.2 B. C.4 D.2
2.如图,在 ABCD中,F是AD延长线上一点,连接BF交DC于点E,则图中相似三角形共有( )对.
A.2对 B.3对 C.4对 D.5对
3.如图所示,给出下列条件:
①;②;③;④;⑤
其中单独能够判定的个数为( )
A.2 B.3 C.4 D.5
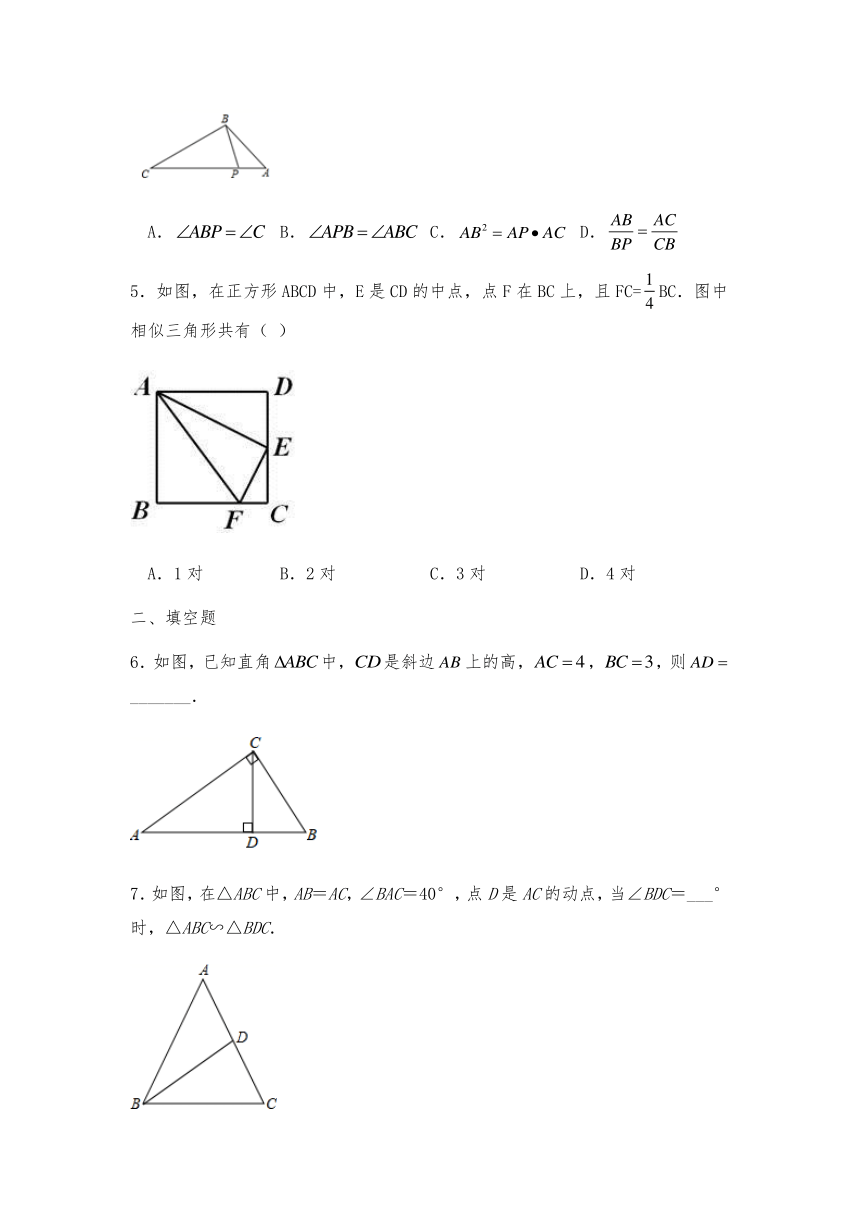
4.如图,已知点在的边上,下列条件中,不能判断的是
A. B. C. D.
5.如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC=BC.图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
二、填空题
6.如图,已知直角中,是斜边上的高,,,则_______.
7.如图,在△ABC中,AB=AC,∠BAC=40°,点D是AC的动点,当∠BDC=___°时,△ABC∽△BDC.
8.矩形纸片按如图所示的方法折纸,并在图中连结后,下面所有正确结论的序号是_________.
①和一定相似;②和不可能全等;
③和不可能全等;④和有可能相似.
9.如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD AB,其中单独能够判定△ABC∽△ACD的有 .
10.如图,在△ABC中,D为AB边上的一点,要使△ABC~△AED成立,还需要添加一个条件为____________.
三、解答题
11.如图,AB AE=AD AC,且∠1=∠2,求证:△ABC∽△ADE.
12.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
13.如图,是的角平分线,延长至点使得.求证: ABE∽ CDE
14.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫作格点.△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.求证:
(1)△ACB ∽△DCE;
(2)EF⊥AB.
.
第二课时
一、单选题
1.如图所示,在△ABC 中,AB=6,AC=4,P 是AC 的中点,过 P 点的直线交AB 于点Q,若以 A、P、Q 为顶点的三角形和以A、B、C为顶点的三角形相似,则AQ 的长为 ( )
A.3 B.3或 C.3或 D.
2.如图,下列条件使△ACD∽△ABC 成立的是( )
A. B. C.AC2=AD·AB D.CD2=AD·BD
3.如图,点在线段上,在的同侧作等腰和等腰,与、分别交于点、.对于下列结论:
①;②;③.其中正确的是( )
A.①②③ B.① C.①② D.②③
4.如图,在矩形中,在上,,交于,连结,则图中与一定相似的三角形是
A. B. C. D.和
5.将矩形OABC如图放置,O为坐标原点,若点A(﹣1,2),点B的纵坐标是,则点C的坐标是( )
A.(4,2) B.(3,) C.(3,) D.(2,)
二、填空题
6.如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为__时,△ADP和△ABC相似.
7.如图,在△ABC与△AED中, ,添加一个条件,使△ABC与△AED相似,这个条件可以是________.
8.如图,在△ABC 中,∠C=90°,BC=6,D,E分别在AB、AC 上,将△ABC沿DE折叠,使点A落在点处,若为CE的中点,则折痕DE的长为___________.
9.如图,在直角△ABC中,∠C=90°,AC=6,BC=8,P、Q分别为边BC、AB上的两个动点,若要使△APQ是等腰三角形且△BPQ是直角三角形,则AQ =________.
三、解答题
10.在△ABC中,CF⊥AB于点F,ED⊥AB于点D,∠1=∠2,求证:△AFG∽△ABC.
11.如图,在中,过点C作,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G,连接AD,CF
求证:四边形AFCD是平行四边形.
若,,,求AB的长.
12.如图,在 ABCD中,对角线AC,BD交于点O,过点O作EO⊥BD,交BA延长线于点E,交AD于点F,若EF=OF,∠CBD=30°,BD=6.求AF的长.
13.如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2,则BC= .
14.如图,已知P是菱形ABCD中CD边上一点,AP交对角线BD于点E,将沿AP翻折得,FP交边BC于点G,.
(1)求证:;
(2)若,,求的长.
第一课时答案
一、单选题
A.B.B.D.C.
二、填空题
6..
7.70
8.①③④
9.①②④.
10.∠B=∠AED 或∠C=∠ADE 或
三、解答题
11.
证明:如图,∵AB AE=AD AC,
∴.
又∵∠1=∠2,
∴∠2+∠BAE=∠1+∠BAE,即∠BAC=∠DAE,
∴△ABC∽△AED.
12.
∵在△ABC中,AB=AC,BD=CD,
∴AD⊥BC.
又∵CE⊥AB,
∴∠ADB=∠CEB=90°,
又∵∠B=∠B,
∴△ABD∽△CBE.
13.
是的角平分线
又
∴ ABE∽ CDE
14.
(1)证明:∵
∴=,
又∵∠ACB=∠DCE=90°,
∴△ACB∽△DCE;
(2)∵△ACB∽△DCE,
∴∠B=∠E,
∵∠B+∠A=90°,
∴∠E+A=90°,
即∠EFA=90°,
∴EF⊥AB.
第二课时答案
一、单选题
B.C.A.B.B.
二、填空题
6.4或9.
7.∠B=∠E(答案不唯一).
8.2
9.或
三、解答题
10.
证明:∵CF⊥AB,ED⊥AB,
∴∠EDB=∠CFA=90°,
∴∠1+∠B=∠2+∠AFG=90°,且∠1=∠2,
∴∠AFG=∠B,且∠FAG=∠GAB,
∴△AFG∽△ABC.
11.
是AC的中点,
,
,
,
在和中,
,
≌,
,
又,即,
四边形AFCD是平行四边形;
,
∽,
,即,
解得:,
四边形AFCD是平行四边形,
,
.
12.
解:方法一:
∵□ABCD,∴AD∥BC,OD=BD=.
∵∠CBD=30°,∴∠ADB=30°.
∵EO⊥BD于O,∴∠DOF=90°.
在Rt△ODF中,tan30°=,∴OF=3.∴FD=6.
过O作OG∥AB,交AD于点G,∴△AEF∽△GOF,∴.
∵EF=OF,∴AF=GF.
∵O是BD中点,∴G是AD中点.
设AF=GF=x,则AD=6+x,∴AG=.
解得x=2,∴AF=2.
方法二:延长EF交BC于H.
由△ODF≌△OHB可知,OH=OF.
∵AD∥BC,∴△EAF∽△EBH,∴.
∵EF=OF,∴.
由方法一的方法,可求BH=6,∴AF=2.
13.
(1)①∵四边形ABCD是正方形,
∴∠BCD=90°,∠BCA=45°,
∵GE⊥BC、GF⊥CD,
∴∠CEG=∠CFG=∠ECF=90°,
∴四边形CEGF是矩形,∠CGE=∠ECG=45°,
∴EG=EC,
∴四边形CEGF是正方形;
②由①知四边形CEGF是正方形,
∴∠CEG=∠B=90°,∠ECG=45°,
∴,GE∥AB,
∴,
故答案为;
(2)连接CG,
由旋转性质知∠BCE=∠ACG=α,
在Rt△CEG和Rt△CBA中,
=、=,
∴=,
∴△ACG∽△BCE,
∴,
∴线段AG与BE之间的数量关系为AG=BE;
(3)∵∠CEF=45°,点B、E、F三点共线,
∴∠BEC=135°,
∵△ACG∽△BCE,
∴∠AGC=∠BEC=135°,
∴∠AGH=∠CAH=45°,
∵∠CHA=∠AHG,
∴△AHG∽△CHA,
∴,
设BC=CD=AD=a,则AC=a,
则由得,
∴AH=a,
则DH=AD﹣AH=a,CH==a,
∴由得,
解得:a=3,即BC=3,
故答案为3.
14.
(1)证明:在菱形ABCD中,BC=CD
∵FPBD
∴∠DEP=∠APF=∠APD,BG=DP,
∴DE=PD
又∵BG=DP ,DE=PD
∴BG=DE .
(2)连结AC,交BD,FP分别为M,N两点.
∵四边形ABCD是菱形
,BM=DM,PN=GN.
∵ABCD
∴∠ABE=∠PDE,∠BAE=∠DPE
在△ABE和△PDE中
∴△ABE∽△PDE
∵DP=DE,
∴ AB=BE
又∵CP:DP=1:3,AP=7,设CP=
DP=DE=3CP=3,AB=BE=4, BD=7,,
在Rt△ADM和Rt△AEM中,
AM2=,
得=2.
,
得.
.
第一课时
一、单选题
1.在△ABC中,三条边的长分别为2、3、4,△A′B′C′的两边长分别为1、1.5,要使△ABC∽△A′B′C′,那么△A′B′C′的第三边长应该是( )
A.2 B. C.4 D.2
2.如图,在 ABCD中,F是AD延长线上一点,连接BF交DC于点E,则图中相似三角形共有( )对.
A.2对 B.3对 C.4对 D.5对
3.如图所示,给出下列条件:
①;②;③;④;⑤
其中单独能够判定的个数为( )
A.2 B.3 C.4 D.5
4.如图,已知点在的边上,下列条件中,不能判断的是
A. B. C. D.
5.如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC=BC.图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
二、填空题
6.如图,已知直角中,是斜边上的高,,,则_______.
7.如图,在△ABC中,AB=AC,∠BAC=40°,点D是AC的动点,当∠BDC=___°时,△ABC∽△BDC.
8.矩形纸片按如图所示的方法折纸,并在图中连结后,下面所有正确结论的序号是_________.
①和一定相似;②和不可能全等;
③和不可能全等;④和有可能相似.
9.如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD AB,其中单独能够判定△ABC∽△ACD的有 .
10.如图,在△ABC中,D为AB边上的一点,要使△ABC~△AED成立,还需要添加一个条件为____________.
三、解答题
11.如图,AB AE=AD AC,且∠1=∠2,求证:△ABC∽△ADE.
12.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
13.如图,是的角平分线,延长至点使得.求证: ABE∽ CDE
14.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫作格点.△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.求证:
(1)△ACB ∽△DCE;
(2)EF⊥AB.
.
第二课时
一、单选题
1.如图所示,在△ABC 中,AB=6,AC=4,P 是AC 的中点,过 P 点的直线交AB 于点Q,若以 A、P、Q 为顶点的三角形和以A、B、C为顶点的三角形相似,则AQ 的长为 ( )
A.3 B.3或 C.3或 D.
2.如图,下列条件使△ACD∽△ABC 成立的是( )
A. B. C.AC2=AD·AB D.CD2=AD·BD
3.如图,点在线段上,在的同侧作等腰和等腰,与、分别交于点、.对于下列结论:
①;②;③.其中正确的是( )
A.①②③ B.① C.①② D.②③
4.如图,在矩形中,在上,,交于,连结,则图中与一定相似的三角形是
A. B. C. D.和
5.将矩形OABC如图放置,O为坐标原点,若点A(﹣1,2),点B的纵坐标是,则点C的坐标是( )
A.(4,2) B.(3,) C.(3,) D.(2,)
二、填空题
6.如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为__时,△ADP和△ABC相似.
7.如图,在△ABC与△AED中, ,添加一个条件,使△ABC与△AED相似,这个条件可以是________.
8.如图,在△ABC 中,∠C=90°,BC=6,D,E分别在AB、AC 上,将△ABC沿DE折叠,使点A落在点处,若为CE的中点,则折痕DE的长为___________.
9.如图,在直角△ABC中,∠C=90°,AC=6,BC=8,P、Q分别为边BC、AB上的两个动点,若要使△APQ是等腰三角形且△BPQ是直角三角形,则AQ =________.
三、解答题
10.在△ABC中,CF⊥AB于点F,ED⊥AB于点D,∠1=∠2,求证:△AFG∽△ABC.
11.如图,在中,过点C作,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G,连接AD,CF
求证:四边形AFCD是平行四边形.
若,,,求AB的长.
12.如图,在 ABCD中,对角线AC,BD交于点O,过点O作EO⊥BD,交BA延长线于点E,交AD于点F,若EF=OF,∠CBD=30°,BD=6.求AF的长.
13.如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2,则BC= .
14.如图,已知P是菱形ABCD中CD边上一点,AP交对角线BD于点E,将沿AP翻折得,FP交边BC于点G,.
(1)求证:;
(2)若,,求的长.
第一课时答案
一、单选题
A.B.B.D.C.
二、填空题
6..
7.70
8.①③④
9.①②④.
10.∠B=∠AED 或∠C=∠ADE 或
三、解答题
11.
证明:如图,∵AB AE=AD AC,
∴.
又∵∠1=∠2,
∴∠2+∠BAE=∠1+∠BAE,即∠BAC=∠DAE,
∴△ABC∽△AED.
12.
∵在△ABC中,AB=AC,BD=CD,
∴AD⊥BC.
又∵CE⊥AB,
∴∠ADB=∠CEB=90°,
又∵∠B=∠B,
∴△ABD∽△CBE.
13.
是的角平分线
又
∴ ABE∽ CDE
14.
(1)证明:∵
∴=,
又∵∠ACB=∠DCE=90°,
∴△ACB∽△DCE;
(2)∵△ACB∽△DCE,
∴∠B=∠E,
∵∠B+∠A=90°,
∴∠E+A=90°,
即∠EFA=90°,
∴EF⊥AB.
第二课时答案
一、单选题
B.C.A.B.B.
二、填空题
6.4或9.
7.∠B=∠E(答案不唯一).
8.2
9.或
三、解答题
10.
证明:∵CF⊥AB,ED⊥AB,
∴∠EDB=∠CFA=90°,
∴∠1+∠B=∠2+∠AFG=90°,且∠1=∠2,
∴∠AFG=∠B,且∠FAG=∠GAB,
∴△AFG∽△ABC.
11.
是AC的中点,
,
,
,
在和中,
,
≌,
,
又,即,
四边形AFCD是平行四边形;
,
∽,
,即,
解得:,
四边形AFCD是平行四边形,
,
.
12.
解:方法一:
∵□ABCD,∴AD∥BC,OD=BD=.
∵∠CBD=30°,∴∠ADB=30°.
∵EO⊥BD于O,∴∠DOF=90°.
在Rt△ODF中,tan30°=,∴OF=3.∴FD=6.
过O作OG∥AB,交AD于点G,∴△AEF∽△GOF,∴.
∵EF=OF,∴AF=GF.
∵O是BD中点,∴G是AD中点.
设AF=GF=x,则AD=6+x,∴AG=.
解得x=2,∴AF=2.
方法二:延长EF交BC于H.
由△ODF≌△OHB可知,OH=OF.
∵AD∥BC,∴△EAF∽△EBH,∴.
∵EF=OF,∴.
由方法一的方法,可求BH=6,∴AF=2.
13.
(1)①∵四边形ABCD是正方形,
∴∠BCD=90°,∠BCA=45°,
∵GE⊥BC、GF⊥CD,
∴∠CEG=∠CFG=∠ECF=90°,
∴四边形CEGF是矩形,∠CGE=∠ECG=45°,
∴EG=EC,
∴四边形CEGF是正方形;
②由①知四边形CEGF是正方形,
∴∠CEG=∠B=90°,∠ECG=45°,
∴,GE∥AB,
∴,
故答案为;
(2)连接CG,
由旋转性质知∠BCE=∠ACG=α,
在Rt△CEG和Rt△CBA中,
=、=,
∴=,
∴△ACG∽△BCE,
∴,
∴线段AG与BE之间的数量关系为AG=BE;
(3)∵∠CEF=45°,点B、E、F三点共线,
∴∠BEC=135°,
∵△ACG∽△BCE,
∴∠AGC=∠BEC=135°,
∴∠AGH=∠CAH=45°,
∵∠CHA=∠AHG,
∴△AHG∽△CHA,
∴,
设BC=CD=AD=a,则AC=a,
则由得,
∴AH=a,
则DH=AD﹣AH=a,CH==a,
∴由得,
解得:a=3,即BC=3,
故答案为3.
14.
(1)证明:在菱形ABCD中,BC=CD
∵FPBD
∴∠DEP=∠APF=∠APD,BG=DP,
∴DE=PD
又∵BG=DP ,DE=PD
∴BG=DE .
(2)连结AC,交BD,FP分别为M,N两点.
∵四边形ABCD是菱形
,BM=DM,PN=GN.
∵ABCD
∴∠ABE=∠PDE,∠BAE=∠DPE
在△ABE和△PDE中
∴△ABE∽△PDE
∵DP=DE,
∴ AB=BE
又∵CP:DP=1:3,AP=7,设CP=
DP=DE=3CP=3,AB=BE=4, BD=7,,
在Rt△ADM和Rt△AEM中,
AM2=,
得=2.
,
得.
.
