21.3实际问题与一元二次方程—动态几何问题 解答题专题训练 人教版九年级数学上册(含答案)
文档属性
| 名称 | 21.3实际问题与一元二次方程—动态几何问题 解答题专题训练 人教版九年级数学上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 601.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 15:33:04 | ||
图片预览




文档简介
2023-2024学年人教版九年级数学上册《21.3实际问题与一元二次方程—动态几何问题》
解答题专题训练(附答案)
一、解答题
1.如图,在边长为的等边三角形中,点从点A开始沿边向点以每秒的速度移动,点从点开始沿边向点以每秒的速度移动.若,分别从A、同时出发,其中任意一点到达目的地后,两点同时停止运动.求经过几秒的面积等于?
2.等腰中,,动点从点出发,沿向点移动,通过点引平行于、的直线与、分别交于点、,问:等于多少厘米时,平行四边形的面积等于.
3.如图,在中,,.点从点开始沿边向点以的速度移动,同时点从点开始沿边向点以的速度移动,另外一点也随之停止运动.
(1)几秒后,四边形的面积等于?
(2)的面积能否等于?请说明理由.
4.如图,在直角梯形中,,.动点P从点D出发,沿射线的方向以每秒2个单位的速度运动,动点Q从点C出发,沿射线 的方向以每秒1个单位的速度向点B运动,点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动的时间为t(秒),当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
5.如图,在中,,点P从A点出发,以的速度向B点移动,点Q从B点出发,以的速度向C点移动,当一个点到达终点时,另一个点也随即停止运动.如果P、Q两点同时出发,经过几秒后的面积等于?
6.如图,菱形中,,交于,,,动点从出发沿方向以每秒匀速直线运动到,动点从出发沿方向以每秒匀速直线运动到,若,同时出发,问出发后几秒钟时,的面积为菱形面积的?
7.如图,中,,,,点从点开始沿边向点以的速度移动,同时点从点开始,沿边向点以的速度移动,点到达点后,点停止运动.
(1)经过后(),的面积等于,求的值;
(2)经过后,(),的长度为,求的值;
(3)的面积能否等于?
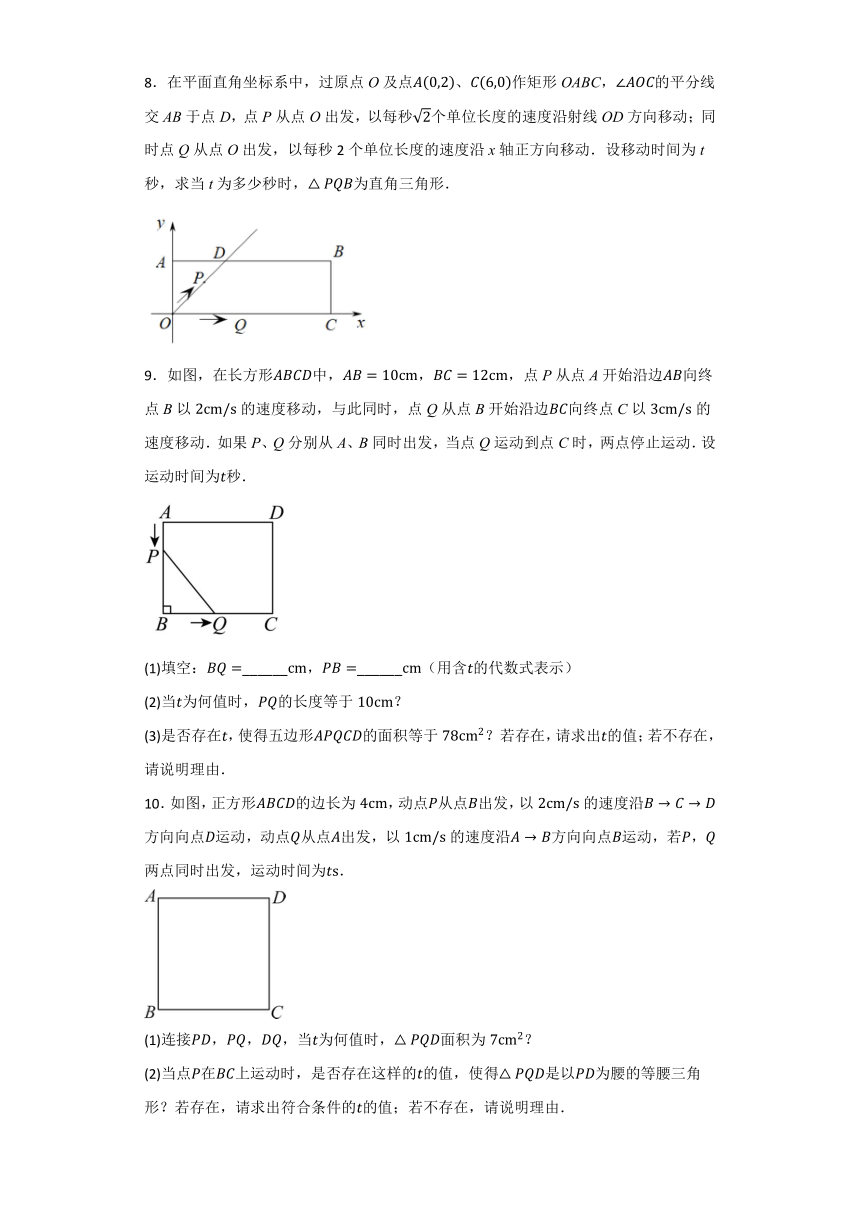
8.在平面直角坐标系中,过原点O及点、作矩形OABC,的平分线交AB于点D,点P从点O出发,以每秒个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒,求当t为多少秒时,为直角三角形.
9.如图,在长方形中,,,点P从点A开始沿边向终点B以的速度移动,与此同时,点Q从点B开始沿边向终点C以的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为秒.
(1)填空:______,______(用含的代数式表示)
(2)当为何值时,的长度等于?
(3)是否存在,使得五边形的面积等于?若存在,请求出的值;若不存在,请说明理由.
10.如图,正方形的边长为,动点从点出发,以的速度沿方向向点运动,动点从点出发,以的速度沿方向向点运动,若,两点同时出发,运动时间为.
(1)连接,,,当为何值时,面积为?
(2)当点在上运动时,是否存在这样的的值,使得是以为腰的等腰三角形?若存在,请求出符合条件的的值;若不存在,请说明理由.
11.如图,在中,,,点从开始沿边向点以的速度移动,与此同时,点从点开始沿边向点以的速度移动.点,同时出发,当点运动到点时,两点停止运动,设运动时间为秒.
(1)填空:___________, ___________;(用含t的代数式表示)
(2)当t为几秒时,的长度等于?
(3)是否存在某一时刻t,使四边形的面积等于面积的?如果存在,求出t的值,如果不存在,请说明理由,
12.如图,在矩形中,,,动点P、Q分别以,的速度从点A,C同时出发,沿规定路线移动.
(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,问经过多长时间P,Q两点之间的距离是?
(2)若点P沿着移动,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间的面积为?
13.如图,已知A、B、C、D为矩形的四个顶点,,,动点P、Q分别从点A、C同时出发,点P以的速度向点B移动,一直到点B为止,点Q以的速度向点D移动.问:
(1)P、Q两点从出发开始几秒时,四边形的面积为?
(2)几秒时点P点Q间的距离是10厘米?
(3)P,Q两点间距离何时最小?
14.如图,在矩形中,,动点P、Q分别从点A、C同时出发,点P以的速度向点B移动,一直到点B为止,点Q以的速度向点D移动(点P停止移动时,点Q也停止移动).设移动时间为t(s).连接,.
(1)用含t的式子表示线段的长:__________;__________.
(2)当t为何值时,P、Q两点间的距离为?
(3)当t为何值时,四边形的形状可能为矩形吗?若可能,求出t的值;若不可能,请说明理由.
15.如图,在矩形中,,点P从点A沿向点B以的速度移动,同时点Q从点B沿边向点C以的速度移动.当其中一点达到终点时,另一点也随之停止.设P,Q两点移动的时间为,求:
(1)当x为何值时,为等腰三角形;
(2)当x为何值时,的面积为;
(3)当x为何值时,为等腰三角形.
16.如图,是边长为6cm的等边三角形,动点,同时从,两点出发,分别沿,匀速移动,它们的速度都是2,当点到达点时,,两点都停止运动,设点的运动时间为,解答下列问题:
(1)当为何值时,是以为直角的直角三角形?
(2)是否存在,使四边形的面积是面积的?若存在,求出的值;若不存在,请说明理由.
17.如图,平面直角坐标系中,已知点,点,过点作轴的平行线,点是在直线上位于第一象限内的一个动点,连接.
(1)求出__________;
(2)若平分,求点的坐标;
(3)已知点是直线上一点,若是以为直角边的等腰直角三角形,求点的坐标.
18.图,在矩形 中,,,,, 分别从 ,,, 出发沿 ,,, 方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时即停止.已知在相同时间内,若 (),则 ,,.
(1)当 为何值时,, 长度相等?
(2)当 为何值时,以 , 为两边,以矩形的边( 或 )的一部分为第三边能构成一个三角形?
(3)当 为何值时,以 ,,, 为顶点的四边形是平行四边形?
参考答案
1.
解:设经过x秒的面积等于,
则,,
过点Q作,垂足为D,
则,
∵等边中,,,
∴,,
∴,
∴,
∴
,
解得 (不合题意,舍去),,
∴.
答:经过2秒的面积等于.
2.解:设,则,由题意可知和均为等腰直角三角形,的面积等于,
依题意可得,
解得:,即长为.
故长为时,平行四边形的面积等于.
3.(1)解: ,,
当运动时间为 时,,
根据题意可得:
,
整理得:,
解得:或,
当时,点重合,不符合题意,舍去,
∴经过1秒钟,四边形的面积等于;
(2)解:的面积不能等于,
理由如下:根据题意可得:
,
整理得:,
,
所列方程没有实数根,
∴的面积不能等于.
4.解:如图1,当时,过点P作于E,
∴,
∵,
∴,
∴,
∴.
∵,
∴,
∴四边形是矩形,
∴,
∴.
解得:;
如图2,当时,过点Q作于E,
同理可证四边形是矩形,
∴,,
∴,
在中,由勾股定理,得,
∴,
解得:;
如图3,当时,过点P作于E,
同理可证明四边形是矩形,
∴,
∴,
∵,
∴,
在中,由勾股定理得,
∴,
∴,
∴,
故方程无解.
综上所述,或时,以B,P,Q三点为顶点的三角形为等腰三角形.
5.解:如图,
过点Q作于E,则.
∵,
∴.
∴.
设经过t秒后的面积等于,
则
根据题意,.
.
.
当时,,不合题意舍去,取.
答:经过2秒后的面积等于.
6.解:设出发后秒时,.
,
,
当时,点在线段上,点在线段上.
由;
解得,(舍去)
,
;
当时,点在线段上,点在线段上,
由;化简为,
此时方程,原方程无实数解;
当时,点在线段上,点在线段上,
由;
解得(舍去),
,
,
综上所述,出发后或时,.
7.(1)解:∵点从点开始沿边向点以的速度移动,
∴,
∵,
∴,
∵点从点开始,沿边向点以的速度移动,
∴,
∵的面积等于,
∴,
即,
解得:,,
∵,,
∴,,
∴,
∴(不符合题意,舍去),
∴,
答:的值为;
(2)解:∵点从点开始沿边向点以的速度移动,
∴,
∵,
∴,
∵点从点开始,沿边向点以的速度移动,
∴,
∵,
∴,
∴,
整理得:,
解得:,,
∵,
∴(不符合题意,舍去),
∴,
答:的值为;
(3)解:的面积不能等于,理由如下:
∵点从点开始沿边向点以的速度移动,
∴,
∵,
∴,
∵点从点开始,沿边向点以的速度移动,
∴,
假设的面积能等于,
∴,
即,
整理得:,
∵,
∴该方程没有实数根,
∴假设不成立,即的面积不能等于.
8.解:根据运动特点可得:,,
∴,
∵射线OD是的平分线,
∴OD也是第一象限的角平分线,
∵第一象限的角平分线的点的横纵坐标相等,
∵点P从点O出发射线OD方向移动,
∴,
∵,
∴,
∴,
根据矩形的性质易得,
则;;;
当为直角三角形时,
时,,
解得;(舍去);
时,,
解得:,
时,
解得:(舍去),
综上,,或秒时,为直角三角形.
9.(1)解:∵P从点A开始沿边向终点B以的速度移动,
∴,
∵,
∴,
∵点Q从点B开始沿边向终点C以的速度移动,
∴;
故答案为:;.
(2)解:由题意得:,
解得:,;
∴当或时,的长度等于;
(3)解:不存在;理由如下:
长方形的面积是:,
使得五边形的面积等于,则的面积为,
∴,
整理得:,
∵,
∴此方程无解,
∴不存在,使得五边形的面积等于.
10.(1)解:如图,当点在上时,此时,根据题意,得:
,,,,,
∵面积为,
∴,
∴,
整理,得:,
解得:.
如图,当点在上时,此时,
∴,
∴,
解得:,
∴当为秒或秒时,面积为.
(2)存在.
如图,当点在上时,
①当时,可得:
,
解得:,(不合题意,舍去),
②当时,可得:
,
整理,得:,
解得:,(不合题意,舍去),
如图,当点在上时,此时,
可知:,,,
∴不存在以为腰的等腰.
∴当为秒或秒时,是以为腰的等腰三角形.
11.解:(1)点从开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动,
, ,
,
故答案为:,;
(2)由题意得,
,
解得:,(不合题意,舍去),
当时,的长等于;
(3)存在,理由如下:
若四边形的面积等于面积的,
的面积等于面积的,
,
,
解得:或,
当时,
当时,,四边形变为三角形,不合题意,舍去,
存在时刻,使四边形的面积等于面积的,的值为2.
12.(1)解:过点P作于E,
设x秒后,点P和点Q的距离是.
,
∴, ;
∴经过或,P、Q两点之间的距离是;
(2)解:连接.设经过后△PBQ的面积为.
①当时,,
∴,即,
解得;
②当时,,
则,
解得(舍去);
③时,,
则,
解得(舍去).
综上所述,经过4秒或6秒,的面积为.
13.(1)解:当运动时间为t秒时,,,
依题意,得:,
解得:.
答:P,Q两点从出发开始到5秒时,四边形的面积为.
(2)设出发秒后、两点间的距离是10厘米.
则,.
作于,
则,
,
解得:或,
∴、出发或秒时,,间的距离是10厘米;
(3),
当时,即时,最小.
14.(1)解:由题意得:,
∵,
∴;
故答案为,;
(2)解:设出发秒后、两点间的距离是.
则,,作于,
∵四边形是矩形,
∴,
∴四边形是矩形,
∴,
∴,
由勾股定理得:,
解得:或,
答:、出发0.6和5.4秒时,,间的距离是;
(3)解:四边形的形状有可能为矩形;理由如下:
当四边形为矩形,则,
即,
解得:.
答:当、出发3秒时四边形为矩形.
15.(1)解:∵四边形是矩形,
∴,,,
根据题意得:,
∴,
当为等腰三角形时,,
∴,
解得:,
即当时,是等腰三角形;
(2)解:由题意得:,
整理得:,
解得:,
答:当x为1或5时,的面积为;
(3)解:根据题意,分两种情况:
①当时,如图1所示:
在和中,由勾股定理得:,,
∴,
解得:或(不合题意舍去),
∴;
②当时,如图2所示:
在和中,,,
∴,
解得:或(不合题意舍去),
∴.
综上所述,当x为或时,是等腰三角形.
16.解:(1)由题意得:,
,
为等边三角形,
,
当点到达点时,,
则,
∵,
,
,即,
解得,符合题意;
(2)不存在,使四边形的面积是面积的,理由如下:
假设存在某一时刻,使四边形的面积是面积的,
由(1)得:,
,
如图,过点作于点,
,
,
,
整理得:,
此方程根的判别式为,方程无解,
所以假设不成立,
即不存在,使四边形的面积是面积的.
解:(1)
如图1,作轴与,
∵,
轴,点是在直线,
(2)设
平分,
解得,
∴点的坐标 或.
(3)设
当,且时,
①如图2,点在直线上方时,
过点作直线则轴于点,过点作于点,
则
又
,解得.
则
则.
②
如图3,由得
解得.
则
∴.
当,且时,如图4
作轴于,轴于,
则,
则,解得,
则,
.
综上,点的坐标为或.
18.(1)解: ,,
时,即 ,
解得: 或 (舍去),
当 为 时,, 长度相等;
(2)解:当点 与点 重合或点 与点 重合时,以 , 为两边,以矩形的边( 或 )的一部分为第三边可能构成一个三角形,
当点 与点 重合时,
由题意得:,
解得:,(舍去),
,
此时点 与点 不重合,
符合题意;
当点 与点 重合时,
由题意得:,
解得:,
此时 ,不符合题意,
点 与点 不能重合.
综上所述,所求的值为:;
(3)解: 当 点到达 点时,,此时 点和 点还未相遇,
点 只能在点 的左侧,
当点 在点 的左侧时,如图 所示:
由题意得:,
解得:(舍去),,
当 时四边形 是平行四边形;
当点 在点 的右侧时,如图 所示:
由题意得:,
解得:(舍去),,
当 时,四边形 是平行四边形;
综上所述,当 或 时,以 ,,, 为顶点的四边形是平行四边形.
解答题专题训练(附答案)
一、解答题
1.如图,在边长为的等边三角形中,点从点A开始沿边向点以每秒的速度移动,点从点开始沿边向点以每秒的速度移动.若,分别从A、同时出发,其中任意一点到达目的地后,两点同时停止运动.求经过几秒的面积等于?
2.等腰中,,动点从点出发,沿向点移动,通过点引平行于、的直线与、分别交于点、,问:等于多少厘米时,平行四边形的面积等于.
3.如图,在中,,.点从点开始沿边向点以的速度移动,同时点从点开始沿边向点以的速度移动,另外一点也随之停止运动.
(1)几秒后,四边形的面积等于?
(2)的面积能否等于?请说明理由.
4.如图,在直角梯形中,,.动点P从点D出发,沿射线的方向以每秒2个单位的速度运动,动点Q从点C出发,沿射线 的方向以每秒1个单位的速度向点B运动,点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动的时间为t(秒),当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
5.如图,在中,,点P从A点出发,以的速度向B点移动,点Q从B点出发,以的速度向C点移动,当一个点到达终点时,另一个点也随即停止运动.如果P、Q两点同时出发,经过几秒后的面积等于?
6.如图,菱形中,,交于,,,动点从出发沿方向以每秒匀速直线运动到,动点从出发沿方向以每秒匀速直线运动到,若,同时出发,问出发后几秒钟时,的面积为菱形面积的?
7.如图,中,,,,点从点开始沿边向点以的速度移动,同时点从点开始,沿边向点以的速度移动,点到达点后,点停止运动.
(1)经过后(),的面积等于,求的值;
(2)经过后,(),的长度为,求的值;
(3)的面积能否等于?
8.在平面直角坐标系中,过原点O及点、作矩形OABC,的平分线交AB于点D,点P从点O出发,以每秒个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒,求当t为多少秒时,为直角三角形.
9.如图,在长方形中,,,点P从点A开始沿边向终点B以的速度移动,与此同时,点Q从点B开始沿边向终点C以的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为秒.
(1)填空:______,______(用含的代数式表示)
(2)当为何值时,的长度等于?
(3)是否存在,使得五边形的面积等于?若存在,请求出的值;若不存在,请说明理由.
10.如图,正方形的边长为,动点从点出发,以的速度沿方向向点运动,动点从点出发,以的速度沿方向向点运动,若,两点同时出发,运动时间为.
(1)连接,,,当为何值时,面积为?
(2)当点在上运动时,是否存在这样的的值,使得是以为腰的等腰三角形?若存在,请求出符合条件的的值;若不存在,请说明理由.
11.如图,在中,,,点从开始沿边向点以的速度移动,与此同时,点从点开始沿边向点以的速度移动.点,同时出发,当点运动到点时,两点停止运动,设运动时间为秒.
(1)填空:___________, ___________;(用含t的代数式表示)
(2)当t为几秒时,的长度等于?
(3)是否存在某一时刻t,使四边形的面积等于面积的?如果存在,求出t的值,如果不存在,请说明理由,
12.如图,在矩形中,,,动点P、Q分别以,的速度从点A,C同时出发,沿规定路线移动.
(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,问经过多长时间P,Q两点之间的距离是?
(2)若点P沿着移动,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间的面积为?
13.如图,已知A、B、C、D为矩形的四个顶点,,,动点P、Q分别从点A、C同时出发,点P以的速度向点B移动,一直到点B为止,点Q以的速度向点D移动.问:
(1)P、Q两点从出发开始几秒时,四边形的面积为?
(2)几秒时点P点Q间的距离是10厘米?
(3)P,Q两点间距离何时最小?
14.如图,在矩形中,,动点P、Q分别从点A、C同时出发,点P以的速度向点B移动,一直到点B为止,点Q以的速度向点D移动(点P停止移动时,点Q也停止移动).设移动时间为t(s).连接,.
(1)用含t的式子表示线段的长:__________;__________.
(2)当t为何值时,P、Q两点间的距离为?
(3)当t为何值时,四边形的形状可能为矩形吗?若可能,求出t的值;若不可能,请说明理由.
15.如图,在矩形中,,点P从点A沿向点B以的速度移动,同时点Q从点B沿边向点C以的速度移动.当其中一点达到终点时,另一点也随之停止.设P,Q两点移动的时间为,求:
(1)当x为何值时,为等腰三角形;
(2)当x为何值时,的面积为;
(3)当x为何值时,为等腰三角形.
16.如图,是边长为6cm的等边三角形,动点,同时从,两点出发,分别沿,匀速移动,它们的速度都是2,当点到达点时,,两点都停止运动,设点的运动时间为,解答下列问题:
(1)当为何值时,是以为直角的直角三角形?
(2)是否存在,使四边形的面积是面积的?若存在,求出的值;若不存在,请说明理由.
17.如图,平面直角坐标系中,已知点,点,过点作轴的平行线,点是在直线上位于第一象限内的一个动点,连接.
(1)求出__________;
(2)若平分,求点的坐标;
(3)已知点是直线上一点,若是以为直角边的等腰直角三角形,求点的坐标.
18.图,在矩形 中,,,,, 分别从 ,,, 出发沿 ,,, 方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时即停止.已知在相同时间内,若 (),则 ,,.
(1)当 为何值时,, 长度相等?
(2)当 为何值时,以 , 为两边,以矩形的边( 或 )的一部分为第三边能构成一个三角形?
(3)当 为何值时,以 ,,, 为顶点的四边形是平行四边形?
参考答案
1.
解:设经过x秒的面积等于,
则,,
过点Q作,垂足为D,
则,
∵等边中,,,
∴,,
∴,
∴,
∴
,
解得 (不合题意,舍去),,
∴.
答:经过2秒的面积等于.
2.解:设,则,由题意可知和均为等腰直角三角形,的面积等于,
依题意可得,
解得:,即长为.
故长为时,平行四边形的面积等于.
3.(1)解: ,,
当运动时间为 时,,
根据题意可得:
,
整理得:,
解得:或,
当时,点重合,不符合题意,舍去,
∴经过1秒钟,四边形的面积等于;
(2)解:的面积不能等于,
理由如下:根据题意可得:
,
整理得:,
,
所列方程没有实数根,
∴的面积不能等于.
4.解:如图1,当时,过点P作于E,
∴,
∵,
∴,
∴,
∴.
∵,
∴,
∴四边形是矩形,
∴,
∴.
解得:;
如图2,当时,过点Q作于E,
同理可证四边形是矩形,
∴,,
∴,
在中,由勾股定理,得,
∴,
解得:;
如图3,当时,过点P作于E,
同理可证明四边形是矩形,
∴,
∴,
∵,
∴,
在中,由勾股定理得,
∴,
∴,
∴,
故方程无解.
综上所述,或时,以B,P,Q三点为顶点的三角形为等腰三角形.
5.解:如图,
过点Q作于E,则.
∵,
∴.
∴.
设经过t秒后的面积等于,
则
根据题意,.
.
.
当时,,不合题意舍去,取.
答:经过2秒后的面积等于.
6.解:设出发后秒时,.
,
,
当时,点在线段上,点在线段上.
由;
解得,(舍去)
,
;
当时,点在线段上,点在线段上,
由;化简为,
此时方程,原方程无实数解;
当时,点在线段上,点在线段上,
由;
解得(舍去),
,
,
综上所述,出发后或时,.
7.(1)解:∵点从点开始沿边向点以的速度移动,
∴,
∵,
∴,
∵点从点开始,沿边向点以的速度移动,
∴,
∵的面积等于,
∴,
即,
解得:,,
∵,,
∴,,
∴,
∴(不符合题意,舍去),
∴,
答:的值为;
(2)解:∵点从点开始沿边向点以的速度移动,
∴,
∵,
∴,
∵点从点开始,沿边向点以的速度移动,
∴,
∵,
∴,
∴,
整理得:,
解得:,,
∵,
∴(不符合题意,舍去),
∴,
答:的值为;
(3)解:的面积不能等于,理由如下:
∵点从点开始沿边向点以的速度移动,
∴,
∵,
∴,
∵点从点开始,沿边向点以的速度移动,
∴,
假设的面积能等于,
∴,
即,
整理得:,
∵,
∴该方程没有实数根,
∴假设不成立,即的面积不能等于.
8.解:根据运动特点可得:,,
∴,
∵射线OD是的平分线,
∴OD也是第一象限的角平分线,
∵第一象限的角平分线的点的横纵坐标相等,
∵点P从点O出发射线OD方向移动,
∴,
∵,
∴,
∴,
根据矩形的性质易得,
则;;;
当为直角三角形时,
时,,
解得;(舍去);
时,,
解得:,
时,
解得:(舍去),
综上,,或秒时,为直角三角形.
9.(1)解:∵P从点A开始沿边向终点B以的速度移动,
∴,
∵,
∴,
∵点Q从点B开始沿边向终点C以的速度移动,
∴;
故答案为:;.
(2)解:由题意得:,
解得:,;
∴当或时,的长度等于;
(3)解:不存在;理由如下:
长方形的面积是:,
使得五边形的面积等于,则的面积为,
∴,
整理得:,
∵,
∴此方程无解,
∴不存在,使得五边形的面积等于.
10.(1)解:如图,当点在上时,此时,根据题意,得:
,,,,,
∵面积为,
∴,
∴,
整理,得:,
解得:.
如图,当点在上时,此时,
∴,
∴,
解得:,
∴当为秒或秒时,面积为.
(2)存在.
如图,当点在上时,
①当时,可得:
,
解得:,(不合题意,舍去),
②当时,可得:
,
整理,得:,
解得:,(不合题意,舍去),
如图,当点在上时,此时,
可知:,,,
∴不存在以为腰的等腰.
∴当为秒或秒时,是以为腰的等腰三角形.
11.解:(1)点从开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动,
, ,
,
故答案为:,;
(2)由题意得,
,
解得:,(不合题意,舍去),
当时,的长等于;
(3)存在,理由如下:
若四边形的面积等于面积的,
的面积等于面积的,
,
,
解得:或,
当时,
当时,,四边形变为三角形,不合题意,舍去,
存在时刻,使四边形的面积等于面积的,的值为2.
12.(1)解:过点P作于E,
设x秒后,点P和点Q的距离是.
,
∴, ;
∴经过或,P、Q两点之间的距离是;
(2)解:连接.设经过后△PBQ的面积为.
①当时,,
∴,即,
解得;
②当时,,
则,
解得(舍去);
③时,,
则,
解得(舍去).
综上所述,经过4秒或6秒,的面积为.
13.(1)解:当运动时间为t秒时,,,
依题意,得:,
解得:.
答:P,Q两点从出发开始到5秒时,四边形的面积为.
(2)设出发秒后、两点间的距离是10厘米.
则,.
作于,
则,
,
解得:或,
∴、出发或秒时,,间的距离是10厘米;
(3),
当时,即时,最小.
14.(1)解:由题意得:,
∵,
∴;
故答案为,;
(2)解:设出发秒后、两点间的距离是.
则,,作于,
∵四边形是矩形,
∴,
∴四边形是矩形,
∴,
∴,
由勾股定理得:,
解得:或,
答:、出发0.6和5.4秒时,,间的距离是;
(3)解:四边形的形状有可能为矩形;理由如下:
当四边形为矩形,则,
即,
解得:.
答:当、出发3秒时四边形为矩形.
15.(1)解:∵四边形是矩形,
∴,,,
根据题意得:,
∴,
当为等腰三角形时,,
∴,
解得:,
即当时,是等腰三角形;
(2)解:由题意得:,
整理得:,
解得:,
答:当x为1或5时,的面积为;
(3)解:根据题意,分两种情况:
①当时,如图1所示:
在和中,由勾股定理得:,,
∴,
解得:或(不合题意舍去),
∴;
②当时,如图2所示:
在和中,,,
∴,
解得:或(不合题意舍去),
∴.
综上所述,当x为或时,是等腰三角形.
16.解:(1)由题意得:,
,
为等边三角形,
,
当点到达点时,,
则,
∵,
,
,即,
解得,符合题意;
(2)不存在,使四边形的面积是面积的,理由如下:
假设存在某一时刻,使四边形的面积是面积的,
由(1)得:,
,
如图,过点作于点,
,
,
,
整理得:,
此方程根的判别式为,方程无解,
所以假设不成立,
即不存在,使四边形的面积是面积的.
解:(1)
如图1,作轴与,
∵,
轴,点是在直线,
(2)设
平分,
解得,
∴点的坐标 或.
(3)设
当,且时,
①如图2,点在直线上方时,
过点作直线则轴于点,过点作于点,
则
又
,解得.
则
则.
②
如图3,由得
解得.
则
∴.
当,且时,如图4
作轴于,轴于,
则,
则,解得,
则,
.
综上,点的坐标为或.
18.(1)解: ,,
时,即 ,
解得: 或 (舍去),
当 为 时,, 长度相等;
(2)解:当点 与点 重合或点 与点 重合时,以 , 为两边,以矩形的边( 或 )的一部分为第三边可能构成一个三角形,
当点 与点 重合时,
由题意得:,
解得:,(舍去),
,
此时点 与点 不重合,
符合题意;
当点 与点 重合时,
由题意得:,
解得:,
此时 ,不符合题意,
点 与点 不能重合.
综上所述,所求的值为:;
(3)解: 当 点到达 点时,,此时 点和 点还未相遇,
点 只能在点 的左侧,
当点 在点 的左侧时,如图 所示:
由题意得:,
解得:(舍去),,
当 时四边形 是平行四边形;
当点 在点 的右侧时,如图 所示:
由题意得:,
解得:(舍去),,
当 时,四边形 是平行四边形;
综上所述,当 或 时,以 ,,, 为顶点的四边形是平行四边形.
同课章节目录
