21.3实际问题与一元二次方程—图形相关问题 解答题专题训练 2023-2024学年人教版九年级数学上册(含答案)
文档属性
| 名称 | 21.3实际问题与一元二次方程—图形相关问题 解答题专题训练 2023-2024学年人教版九年级数学上册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 385.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 15:37:49 | ||
图片预览



文档简介
2023-2024学年人教版九年级数学上册《21.3实际问题与一元二次方程—图形相关问题》
解答题专题训练(附答案)
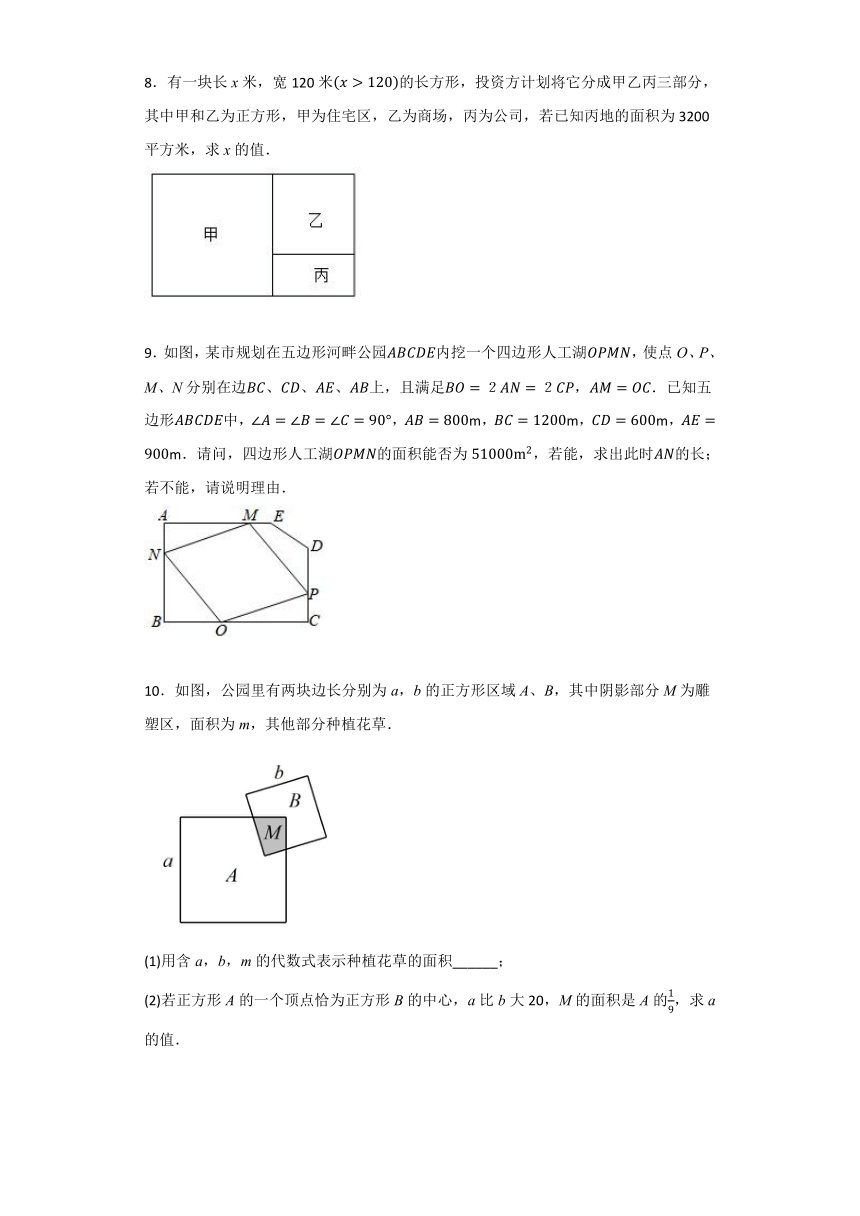
1.如图,有一块长为30米,宽为20米的矩形场地,计划在该场地上修建两条互相垂直的小道,横向小道与竖向小道的宽比为,余下矩形场地建成草坪,草坪的面积为486平方米,请求出横向小道的宽.
2.如图,某小区矩形绿地的长、宽分别为,,现计划对其进行扩充,将绿地的长、宽增加相同的长度后,得到一个新的矩形绿地,若扩充后的矩形绿地面积为,求新的矩形绿地的长与宽.
3.某公园中有一块长为32米,宽为20米的矩形花坛,现在要在花坛中间修建一条如图所示的文化长廊,已知长廊的宽度均相等,且横纵相交成直角,若要使花坛的种植面积为540平方米,问长廊的宽度应为多少米?
4.有长为30米的篱笆,一面利用墙(墙的最大可用长度为12米),围成中间隔有一道篱笆(平行于AB)的矩形花圃,设花圃的一边AB为x米,面积为平方米.
(1)用含x的代数式表示,并求出x的取值范围;
(2)如果要围成面积为63平方米的花圃,AB的长是多少
5.如图,有一农户要建一个矩形鸡舍,鸡舍的一边利用长为的墙,另外三边用长的篱笆围成,为方便进出,在垂直于墙的一边上留一个宽的门.
(1)矩形的边长分别为多少时,鸡舍面积为?
(2)鸡舍面积能否达到?
6.用总长的木板制作矩形置物架(如图),已知该置物架上面部分为正方形,下面部分是两个全等的矩形和矩形,中间部分为矩形.已知,设正方形的边长为.
(1)当时,的长为________;
(2)置物架的高的长为________(用含的代数式表示);
(3)为了便于置放物品,的高度不小于,若矩形的面积为,求的值.
7.某学校在“美化校园,幸福学习”活动中,计划利用如图所示的直角墙角(阴影部分,两边足够长),用长的篱笆围成一个矩形花园(篱笆只围AB,AD两边).
(1)若花园的面积为,求AB的长;
(2)若在直角墙角内点P处有一棵桂花树,且到墙CD的距离为,若要将这棵树围在矩形花园内(含边界,不考虑树的粗细),问该花园的面积能否为?若能,求出AB的长;若不能,请说明理由.
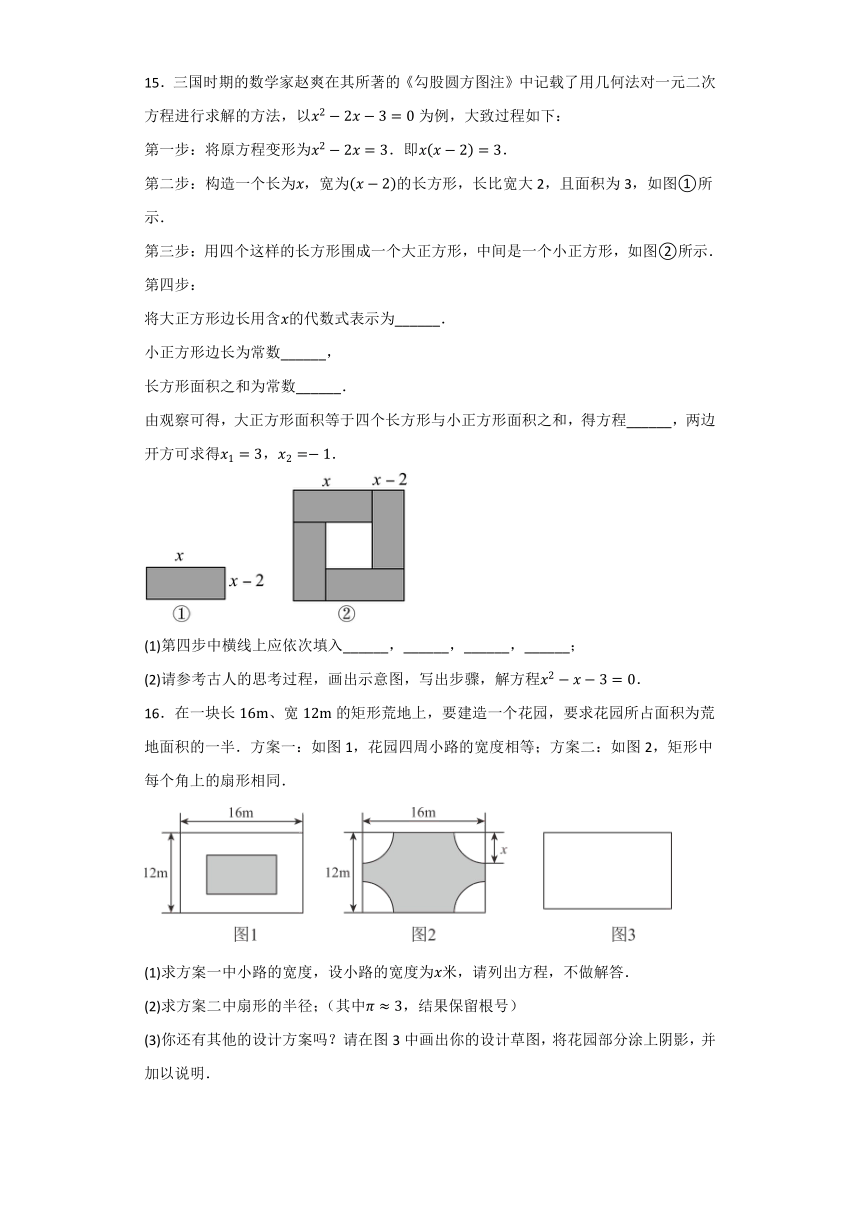
8.有一块长x米,宽120米的长方形,投资方计划将它分成甲乙丙三部分,其中甲和乙为正方形,甲为住宅区,乙为商场,丙为公司,若已知丙地的面积为3200平方米,求x的值.
9.如图,某市规划在五边形河畔公园内挖一个四边形人工湖,使点O、P、M、N分别在边、、、上,且满足,.已知五边形中,,m,m,m,m.请问,四边形人工湖的面积能否为,若能,求出此时的长;若不能,请说明理由.
10.如图,公园里有两块边长分别为a,b的正方形区域A、B,其中阴影部分M为雕塑区,面积为m,其他部分种植花草.
(1)用含a,b,m的代数式表示种植花草的面积______;
(2)若正方形A的一个顶点恰为正方形B的中心,a比b大20,M的面积是A的,求a的值.
11.如图,在平行四边形中,E,F是直线上的两点,.
(1)求证:四边形是平行四边形;
(2)若,,,且,求的长.
12.在正方形中,点为中点,连接并延长交延长线于点,点在上,,连接并延长交延长线于,连接.
(1)求证:四边形为菱形;
(2)若,求四边形的面积.
13.在某会议场馆的建设过程中,为了美化地面,选用相同规格的黑白两色的正方形瓷砖铺设长方形地面,观察如图所示的图形,并解答下列问题:
(1)按上述铺设方案,若铺一块长方形地面共用了506块的瓷砖,求此时的值.
(2)是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明理由.
14.有一块长、宽的矩形铁皮.
(1)如图1,如果在铁皮的四个角裁去四个边长一样的正方形后,将其折成底面积为的无盖长方体盒子,求裁去的正方形的边长;
(2)由于需要,计划制作一个有盖的长方体盒子,为了合理利用材料,某学生设计了如图2所示的裁剪方案,阴影部分为裁剪下来的边角料,其中左侧的两个阴影部分为正方形,问能否折出底面积为的有盖盒子?如果能,请求出盒子的体积;如果不能,请说明理由.
15.三国时期的数学家赵爽在其所著的《勾股圆方图注》中记载了用几何法对一元二次方程进行求解的方法,以为例,大致过程如下:
第一步:将原方程变形为.即.
第二步:构造一个长为,宽为的长方形,长比宽大2,且面积为3,如图①所示.
第三步:用四个这样的长方形围成一个大正方形,中间是一个小正方形,如图②所示.
第四步:
将大正方形边长用含的代数式表示为______.
小正方形边长为常数______,
长方形面积之和为常数______.
由观察可得,大正方形面积等于四个长方形与小正方形面积之和,得方程______,两边开方可求得,.
(1)第四步中横线上应依次填入______,______,______,______;
(2)请参考古人的思考过程,画出示意图,写出步骤,解方程.
16.在一块长、宽的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半.方案一:如图1,花园四周小路的宽度相等;方案二:如图2,矩形中每个角上的扇形相同.
(1)求方案一中小路的宽度,设小路的宽度为米,请列出方程,不做解答.
(2)求方案二中扇形的半径;(其中,结果保留根号)
(3)你还有其他的设计方案吗?请在图3中画出你的设计草图,将花园部分涂上阴影,并加以说明.
17.如图,一架长的梯子斜靠在竖直的墙上,此时点到墙底端点的距离为,如果梯子的顶端沿墙下滑,那么点将向外移动多少米?
(1)请你将下面的解答过程补充完整.
解:设点将向外移动,即,
则,,
而,则在中,由,
得方程为__________;
解得_________;_______;
∴点将向外移动________m.
(2)①如果将“下滑”改为“下滑”,那么该题的答案会是吗?为什么?
②梯子的顶端从点处沿墙下滑的距离与点向外移动的距离有可能相等吗?为什么?
18.如图1,有一长方形菜地,长比宽多20米.求菜地的面积.
老师在黑板上的板书:
(1)请根据老师的板书说出x的实际意义:__________________;
(2)请用含x的多项式表示菜地的面积为:__________________;
(3)如图2,经测量菜地的长为120米.张老爹为了扩大菜地面积,向周围开垦荒地,已知四周开垦的菜地宽度均为a米,通过计算说明菜地开垦后的面积(结果用含a的多项式表示);
(4)当米时,求菜地开垦后的面积;
19.下面是张老师数学课堂教学实践活动的一个片段:
【问题背景】如图1,一副三角板的直角顶点重合,两条直角边分别共线,将它们分别记作,.其中,,,.现固定三角板,将三角板绕点逆时针旋转,旋转角记为,射线与射线交于点,在射线上取一点,使,连接CQ.
(1)【特例探究】如图2,当时,直接写出和的数量关系和位置关系.
(2)【归纳证明】如图3,当点在线段BC上时,【特例探究】中得到的结论是否成立,若成立,请给出证明;若不成立,请说明理由.
(3)【类比迁移】当点在线段延长线上时,请直接写出【特例探究】中结论是否成立,不必说明理由.
(4)【拓展应用】连接.若,的面积等于,请直接写出的长.
20.在学习《完全平方公式》时,某数学学习小组发现:已知,,可以在不求、的值的情况下,求出的值.具体做法如下:
.
(1)若,则______;
(2)若满足,求的值,同样可以应用上述方法解决问题.具体操作如下:
解:设,,
则,,
所以.
请参照上述方法解决下列问题:若,求的值;
(3)如图,某校“园艺”社团在三面靠墙的空地上,用长12米的篱笆(不含墙)围成一个长方形花圃ABCD,花圃ABCD的面积为20平方米,其中墙AD足够长,墙墙AD,墙墙AD,米.随着学校“园艺”社团成员的增加,学校在花圃旁分别以边向外各扩建两个正方形花圃,以边向外扩建一个正方形花圃(如图所示虚线区域部分),请问新扩建花圃的总面积为______平方米.
参考答案
1.解:设横向小道宽为米,则坚向小道的宽为米,
根据题意得:,
整理得:,
解得:(舍去),
(米),
答:横向小道的宽为2米.
2.解:设将绿地的长、宽增加,则新的矩形绿地的长为,宽为,
根据题意得:,
整理得:,
解得:,(不符合题意,舍去),
,.
答:新的矩形绿地的长为,宽为.
3.解:设长廊的宽度应为x米.
解得,(舍去)
答:长廊的宽应为2米.
4.(1)解:的长为米,且篱笆的总长度为米,
的长为米.
花圃的面积.
,
.
.
(2)解:依题意得:,
整理得:,
解得:(不符合题意,舍去),.
答:的长是米.
5.(1)解:设矩形鸡舍垂直于房墙的一边长为,则矩形鸡舍的另一边长为.
依题意,得,
解得,.
当时,(舍去),
当时,.
答:矩形鸡舍的长为,宽为;
(2)解:当,
则,
整理得:,
则,
故所围成鸡舍面积不能为平方米.
6.(1)解:当时,则,,
故答案为:5;
(2)置物架的高的长为(),
故答案为:;
(3)根据题意,由(2)得,,
解得,,,
当时,的长为,的高度为,小于,舍去;
当时,的长为,的高度为,不小于,符合题意.
∴
7.(1)解:米, 米,
由题意得:,
解得:,,
答:的长为米或米;
(2)解:花园的面积不能为米,理由如下:
米, 米,
由题意得:,
解得:,
当时,,
即当米,米米,这棵树没有被围在花园内,
将这棵树围在矩形花园内含边界,不考虑树的粗细,则花园的面积不能为米.
8.解:依题意得,丙地的长为米,宽为米,
,
整理得,
解得:,,
的值为160或200.
9.解:能,理由如下:
如图,延长,于,
四边形是矩形,
,,
,,
,,
设,则,
,,
,,,
,,
若四边形人工湖的面积为,
,
整理得:,
解得:,,
故:能,的长为m或m.
10.(1)解:种植花草的面积;
(2)依题意得,,,.
列方程得,,
解得,
∵,
∴.
11.(1)证明:如图,连接交于点,
四边形是平行四边形,
,
,
,即,
四边形是平行四边形.
(2)解:四边形是平行四边形,,
,
,,
,
设,则,,
,
,
在中,,即,
解得或(不符合题意,舍去),
则的长为.
12.解:(1)∵ 四边形是正方形,
∴,即,
∴.
∵点E为中点,
∴.
又∵,
∴,
∴.
同理可证,,
∴,
∴,
∴,
∴四边形为平行四边形.
∵,
∴.
又∵,
∴,
∴,
∴四边形为菱形;
(2)设的长为x.
∵,
∴,
∴.
∵四边形为菱形,
∴.
∵在中,,
∴
解得:(舍),
∴,,
∴.
13.(1)解:由题意,得,
∴,
解得,(舍去).
答:此时的值为20.
(2)∵图形黑砖的数量为:,
白色转的数量为:,
当黑白砖块数相等时,.
整理得.
解得,.
由题意可知为整数,故不存在黑砖白块数相等的情形.
14.解:(1)设小正方形的边长为 .得:
,
解得:(舍去),.
答:裁去的正方形的边长为2.
(2)能;
设小正方形的边长为 .得:
,
解得:(舍去),.
体积为
15.(1)解:根据题意可得:
大正方形的边长为:,
小正方形的边长为:,
长方形面积之和为:,
大正方形面积等于四个长方形与小正方形面积之和,
,
故答案为:,2,12,;
(2)解:第一步:将原方程变形为,即,
第二步:构造成一个长为,宽为的长方形,长比宽大1,且面积为3,
第三步:用四个这样的长方形围城一个大正方形,中间是一个小正方形,如图所示,
第四步:
将大正方形边长用含的代数式表示为,
小正方形边长为常数,
长方形面积之和为常数,
由观察可得,大正方形面积等于四个长方形与小正方形面积之和,
得方程,
两边开方可求得,.
16.(1)解:设小路的宽度为米,
由题意得:;
(2)设扇形的半径为r米,
∵四个角上的四个扇形可合并成一个圆,
∴,
解得,
答:扇形的半径为米;
(3)设计方案如图所示:将矩形荒地分成四个全等的矩形,连接对角线,根据矩形的性质可得阴影部分的面积等于荒地面积的一半.
17.(1)解:补全解答过程:
在中,
∵,,
,,
∴,
解得:,(不合题意,舍去),
∴点将向外移动.
故答案为:;;(不合题意,舍去);.
(2)①不会.
理由:
若,
则,
,
∵,,
∴,
∴该题的答案不会是;
②有可能相等.
理由:设梯子的顶端从点处下滑,点将向外移动,则有:
,
整理,得:,
解得:,(不合题意,舍去),
∴当梯子的顶端从点处下滑时,点也向外移动,即梯子的顶端从点沿墙下滑的距离与点向外移动的距离相等.
18.(1)解:由题意得:x的实际意义是菜地的宽度;
(2)解:设菜地的宽度为x,则长度为,
∴菜地的面积为:;
(3)解:∵菜地的长为120米,
∴菜地的宽为100米,
∵四周开垦的菜地宽度均为a米,
∴开垦后菜地的长为米,菜地的宽为米,
∴开垦后菜地的面积为:
=
(4)解:由(3)得:开垦后菜地的面积为:,
当时,原式=
19.解:(1)特例探究,
∵,
∴,
∴.
∵,∴.
在△ABP和△ACQ中,
∴.
∴,.
∴.
∴.
(2)归纳证明:结论成立.
证明:∵,
∴,
∴.
∵,∴.
在△ABP和△ACQ中,
∴.
∴,.
∴.
∴.
(3)类比迁移:结论成立.
证明:∵,
∴,
∴.
∵,
∴.
在△ABP和△ACQ中,
∴.
∴,.
∴.
∴.
(4)连接.若,的面积等于,请直接写出
拓展应用
解:∵,,
设,则,
当点在线段上时,
∴,
∴ ,
即,
解得:或,
∴,
当点在的延长线上时,
∴,
∴ ,
即,
解得:或(舍去),
∴,
综上所述,的长为或.
20.(1)解:.
(2)解:设,,
则,,
所以.
(3)解:∵四边形长方形,
∴,
∵,
∴,
设米,则米
由题意知,解得或,经检验,均符合题意
①当时,
∴新扩建花圃的总面积为:(平方米);
②当时,,
新扩建花圃的总面积为:(平方米) .
综上,新扩建花圃的总面积为116平方米.
故答案为116.
解答题专题训练(附答案)
1.如图,有一块长为30米,宽为20米的矩形场地,计划在该场地上修建两条互相垂直的小道,横向小道与竖向小道的宽比为,余下矩形场地建成草坪,草坪的面积为486平方米,请求出横向小道的宽.
2.如图,某小区矩形绿地的长、宽分别为,,现计划对其进行扩充,将绿地的长、宽增加相同的长度后,得到一个新的矩形绿地,若扩充后的矩形绿地面积为,求新的矩形绿地的长与宽.
3.某公园中有一块长为32米,宽为20米的矩形花坛,现在要在花坛中间修建一条如图所示的文化长廊,已知长廊的宽度均相等,且横纵相交成直角,若要使花坛的种植面积为540平方米,问长廊的宽度应为多少米?
4.有长为30米的篱笆,一面利用墙(墙的最大可用长度为12米),围成中间隔有一道篱笆(平行于AB)的矩形花圃,设花圃的一边AB为x米,面积为平方米.
(1)用含x的代数式表示,并求出x的取值范围;
(2)如果要围成面积为63平方米的花圃,AB的长是多少
5.如图,有一农户要建一个矩形鸡舍,鸡舍的一边利用长为的墙,另外三边用长的篱笆围成,为方便进出,在垂直于墙的一边上留一个宽的门.
(1)矩形的边长分别为多少时,鸡舍面积为?
(2)鸡舍面积能否达到?
6.用总长的木板制作矩形置物架(如图),已知该置物架上面部分为正方形,下面部分是两个全等的矩形和矩形,中间部分为矩形.已知,设正方形的边长为.
(1)当时,的长为________;
(2)置物架的高的长为________(用含的代数式表示);
(3)为了便于置放物品,的高度不小于,若矩形的面积为,求的值.
7.某学校在“美化校园,幸福学习”活动中,计划利用如图所示的直角墙角(阴影部分,两边足够长),用长的篱笆围成一个矩形花园(篱笆只围AB,AD两边).
(1)若花园的面积为,求AB的长;
(2)若在直角墙角内点P处有一棵桂花树,且到墙CD的距离为,若要将这棵树围在矩形花园内(含边界,不考虑树的粗细),问该花园的面积能否为?若能,求出AB的长;若不能,请说明理由.
8.有一块长x米,宽120米的长方形,投资方计划将它分成甲乙丙三部分,其中甲和乙为正方形,甲为住宅区,乙为商场,丙为公司,若已知丙地的面积为3200平方米,求x的值.
9.如图,某市规划在五边形河畔公园内挖一个四边形人工湖,使点O、P、M、N分别在边、、、上,且满足,.已知五边形中,,m,m,m,m.请问,四边形人工湖的面积能否为,若能,求出此时的长;若不能,请说明理由.
10.如图,公园里有两块边长分别为a,b的正方形区域A、B,其中阴影部分M为雕塑区,面积为m,其他部分种植花草.
(1)用含a,b,m的代数式表示种植花草的面积______;
(2)若正方形A的一个顶点恰为正方形B的中心,a比b大20,M的面积是A的,求a的值.
11.如图,在平行四边形中,E,F是直线上的两点,.
(1)求证:四边形是平行四边形;
(2)若,,,且,求的长.
12.在正方形中,点为中点,连接并延长交延长线于点,点在上,,连接并延长交延长线于,连接.
(1)求证:四边形为菱形;
(2)若,求四边形的面积.
13.在某会议场馆的建设过程中,为了美化地面,选用相同规格的黑白两色的正方形瓷砖铺设长方形地面,观察如图所示的图形,并解答下列问题:
(1)按上述铺设方案,若铺一块长方形地面共用了506块的瓷砖,求此时的值.
(2)是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明理由.
14.有一块长、宽的矩形铁皮.
(1)如图1,如果在铁皮的四个角裁去四个边长一样的正方形后,将其折成底面积为的无盖长方体盒子,求裁去的正方形的边长;
(2)由于需要,计划制作一个有盖的长方体盒子,为了合理利用材料,某学生设计了如图2所示的裁剪方案,阴影部分为裁剪下来的边角料,其中左侧的两个阴影部分为正方形,问能否折出底面积为的有盖盒子?如果能,请求出盒子的体积;如果不能,请说明理由.
15.三国时期的数学家赵爽在其所著的《勾股圆方图注》中记载了用几何法对一元二次方程进行求解的方法,以为例,大致过程如下:
第一步:将原方程变形为.即.
第二步:构造一个长为,宽为的长方形,长比宽大2,且面积为3,如图①所示.
第三步:用四个这样的长方形围成一个大正方形,中间是一个小正方形,如图②所示.
第四步:
将大正方形边长用含的代数式表示为______.
小正方形边长为常数______,
长方形面积之和为常数______.
由观察可得,大正方形面积等于四个长方形与小正方形面积之和,得方程______,两边开方可求得,.
(1)第四步中横线上应依次填入______,______,______,______;
(2)请参考古人的思考过程,画出示意图,写出步骤,解方程.
16.在一块长、宽的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半.方案一:如图1,花园四周小路的宽度相等;方案二:如图2,矩形中每个角上的扇形相同.
(1)求方案一中小路的宽度,设小路的宽度为米,请列出方程,不做解答.
(2)求方案二中扇形的半径;(其中,结果保留根号)
(3)你还有其他的设计方案吗?请在图3中画出你的设计草图,将花园部分涂上阴影,并加以说明.
17.如图,一架长的梯子斜靠在竖直的墙上,此时点到墙底端点的距离为,如果梯子的顶端沿墙下滑,那么点将向外移动多少米?
(1)请你将下面的解答过程补充完整.
解:设点将向外移动,即,
则,,
而,则在中,由,
得方程为__________;
解得_________;_______;
∴点将向外移动________m.
(2)①如果将“下滑”改为“下滑”,那么该题的答案会是吗?为什么?
②梯子的顶端从点处沿墙下滑的距离与点向外移动的距离有可能相等吗?为什么?
18.如图1,有一长方形菜地,长比宽多20米.求菜地的面积.
老师在黑板上的板书:
(1)请根据老师的板书说出x的实际意义:__________________;
(2)请用含x的多项式表示菜地的面积为:__________________;
(3)如图2,经测量菜地的长为120米.张老爹为了扩大菜地面积,向周围开垦荒地,已知四周开垦的菜地宽度均为a米,通过计算说明菜地开垦后的面积(结果用含a的多项式表示);
(4)当米时,求菜地开垦后的面积;
19.下面是张老师数学课堂教学实践活动的一个片段:
【问题背景】如图1,一副三角板的直角顶点重合,两条直角边分别共线,将它们分别记作,.其中,,,.现固定三角板,将三角板绕点逆时针旋转,旋转角记为,射线与射线交于点,在射线上取一点,使,连接CQ.
(1)【特例探究】如图2,当时,直接写出和的数量关系和位置关系.
(2)【归纳证明】如图3,当点在线段BC上时,【特例探究】中得到的结论是否成立,若成立,请给出证明;若不成立,请说明理由.
(3)【类比迁移】当点在线段延长线上时,请直接写出【特例探究】中结论是否成立,不必说明理由.
(4)【拓展应用】连接.若,的面积等于,请直接写出的长.
20.在学习《完全平方公式》时,某数学学习小组发现:已知,,可以在不求、的值的情况下,求出的值.具体做法如下:
.
(1)若,则______;
(2)若满足,求的值,同样可以应用上述方法解决问题.具体操作如下:
解:设,,
则,,
所以.
请参照上述方法解决下列问题:若,求的值;
(3)如图,某校“园艺”社团在三面靠墙的空地上,用长12米的篱笆(不含墙)围成一个长方形花圃ABCD,花圃ABCD的面积为20平方米,其中墙AD足够长,墙墙AD,墙墙AD,米.随着学校“园艺”社团成员的增加,学校在花圃旁分别以边向外各扩建两个正方形花圃,以边向外扩建一个正方形花圃(如图所示虚线区域部分),请问新扩建花圃的总面积为______平方米.
参考答案
1.解:设横向小道宽为米,则坚向小道的宽为米,
根据题意得:,
整理得:,
解得:(舍去),
(米),
答:横向小道的宽为2米.
2.解:设将绿地的长、宽增加,则新的矩形绿地的长为,宽为,
根据题意得:,
整理得:,
解得:,(不符合题意,舍去),
,.
答:新的矩形绿地的长为,宽为.
3.解:设长廊的宽度应为x米.
解得,(舍去)
答:长廊的宽应为2米.
4.(1)解:的长为米,且篱笆的总长度为米,
的长为米.
花圃的面积.
,
.
.
(2)解:依题意得:,
整理得:,
解得:(不符合题意,舍去),.
答:的长是米.
5.(1)解:设矩形鸡舍垂直于房墙的一边长为,则矩形鸡舍的另一边长为.
依题意,得,
解得,.
当时,(舍去),
当时,.
答:矩形鸡舍的长为,宽为;
(2)解:当,
则,
整理得:,
则,
故所围成鸡舍面积不能为平方米.
6.(1)解:当时,则,,
故答案为:5;
(2)置物架的高的长为(),
故答案为:;
(3)根据题意,由(2)得,,
解得,,,
当时,的长为,的高度为,小于,舍去;
当时,的长为,的高度为,不小于,符合题意.
∴
7.(1)解:米, 米,
由题意得:,
解得:,,
答:的长为米或米;
(2)解:花园的面积不能为米,理由如下:
米, 米,
由题意得:,
解得:,
当时,,
即当米,米米,这棵树没有被围在花园内,
将这棵树围在矩形花园内含边界,不考虑树的粗细,则花园的面积不能为米.
8.解:依题意得,丙地的长为米,宽为米,
,
整理得,
解得:,,
的值为160或200.
9.解:能,理由如下:
如图,延长,于,
四边形是矩形,
,,
,,
,,
设,则,
,,
,,,
,,
若四边形人工湖的面积为,
,
整理得:,
解得:,,
故:能,的长为m或m.
10.(1)解:种植花草的面积;
(2)依题意得,,,.
列方程得,,
解得,
∵,
∴.
11.(1)证明:如图,连接交于点,
四边形是平行四边形,
,
,
,即,
四边形是平行四边形.
(2)解:四边形是平行四边形,,
,
,,
,
设,则,,
,
,
在中,,即,
解得或(不符合题意,舍去),
则的长为.
12.解:(1)∵ 四边形是正方形,
∴,即,
∴.
∵点E为中点,
∴.
又∵,
∴,
∴.
同理可证,,
∴,
∴,
∴,
∴四边形为平行四边形.
∵,
∴.
又∵,
∴,
∴,
∴四边形为菱形;
(2)设的长为x.
∵,
∴,
∴.
∵四边形为菱形,
∴.
∵在中,,
∴
解得:(舍),
∴,,
∴.
13.(1)解:由题意,得,
∴,
解得,(舍去).
答:此时的值为20.
(2)∵图形黑砖的数量为:,
白色转的数量为:,
当黑白砖块数相等时,.
整理得.
解得,.
由题意可知为整数,故不存在黑砖白块数相等的情形.
14.解:(1)设小正方形的边长为 .得:
,
解得:(舍去),.
答:裁去的正方形的边长为2.
(2)能;
设小正方形的边长为 .得:
,
解得:(舍去),.
体积为
15.(1)解:根据题意可得:
大正方形的边长为:,
小正方形的边长为:,
长方形面积之和为:,
大正方形面积等于四个长方形与小正方形面积之和,
,
故答案为:,2,12,;
(2)解:第一步:将原方程变形为,即,
第二步:构造成一个长为,宽为的长方形,长比宽大1,且面积为3,
第三步:用四个这样的长方形围城一个大正方形,中间是一个小正方形,如图所示,
第四步:
将大正方形边长用含的代数式表示为,
小正方形边长为常数,
长方形面积之和为常数,
由观察可得,大正方形面积等于四个长方形与小正方形面积之和,
得方程,
两边开方可求得,.
16.(1)解:设小路的宽度为米,
由题意得:;
(2)设扇形的半径为r米,
∵四个角上的四个扇形可合并成一个圆,
∴,
解得,
答:扇形的半径为米;
(3)设计方案如图所示:将矩形荒地分成四个全等的矩形,连接对角线,根据矩形的性质可得阴影部分的面积等于荒地面积的一半.
17.(1)解:补全解答过程:
在中,
∵,,
,,
∴,
解得:,(不合题意,舍去),
∴点将向外移动.
故答案为:;;(不合题意,舍去);.
(2)①不会.
理由:
若,
则,
,
∵,,
∴,
∴该题的答案不会是;
②有可能相等.
理由:设梯子的顶端从点处下滑,点将向外移动,则有:
,
整理,得:,
解得:,(不合题意,舍去),
∴当梯子的顶端从点处下滑时,点也向外移动,即梯子的顶端从点沿墙下滑的距离与点向外移动的距离相等.
18.(1)解:由题意得:x的实际意义是菜地的宽度;
(2)解:设菜地的宽度为x,则长度为,
∴菜地的面积为:;
(3)解:∵菜地的长为120米,
∴菜地的宽为100米,
∵四周开垦的菜地宽度均为a米,
∴开垦后菜地的长为米,菜地的宽为米,
∴开垦后菜地的面积为:
=
(4)解:由(3)得:开垦后菜地的面积为:,
当时,原式=
19.解:(1)特例探究,
∵,
∴,
∴.
∵,∴.
在△ABP和△ACQ中,
∴.
∴,.
∴.
∴.
(2)归纳证明:结论成立.
证明:∵,
∴,
∴.
∵,∴.
在△ABP和△ACQ中,
∴.
∴,.
∴.
∴.
(3)类比迁移:结论成立.
证明:∵,
∴,
∴.
∵,
∴.
在△ABP和△ACQ中,
∴.
∴,.
∴.
∴.
(4)连接.若,的面积等于,请直接写出
拓展应用
解:∵,,
设,则,
当点在线段上时,
∴,
∴ ,
即,
解得:或,
∴,
当点在的延长线上时,
∴,
∴ ,
即,
解得:或(舍去),
∴,
综上所述,的长为或.
20.(1)解:.
(2)解:设,,
则,,
所以.
(3)解:∵四边形长方形,
∴,
∵,
∴,
设米,则米
由题意知,解得或,经检验,均符合题意
①当时,
∴新扩建花圃的总面积为:(平方米);
②当时,,
新扩建花圃的总面积为:(平方米) .
综上,新扩建花圃的总面积为116平方米.
故答案为116.
同课章节目录
