2.5等腰三角形的轴对称性 练习 苏科版数学八年级上册(无答案)
文档属性
| 名称 | 2.5等腰三角形的轴对称性 练习 苏科版数学八年级上册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 448.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 16:19:08 | ||
图片预览



文档简介
2.5等腰三角形的轴对称性(等边三角形)
知识梳理 【知识点1】等边三角形 等边三角形定义:三边都相等的三角形叫等边三角形. 特别说明:由定义可知,等边三角形是一种特殊的等腰三角形.也就是说等腰三角形包括等边三角形. 等边三角形的性质:等边三角形三个内角都相等,并且每一个内角都等于60°. 等边三角形的轴对称性:有3条对称轴,即3条高所在的直线或3条中线所在的直线或3条角平分线所在的直线。 等边三角形的判定:
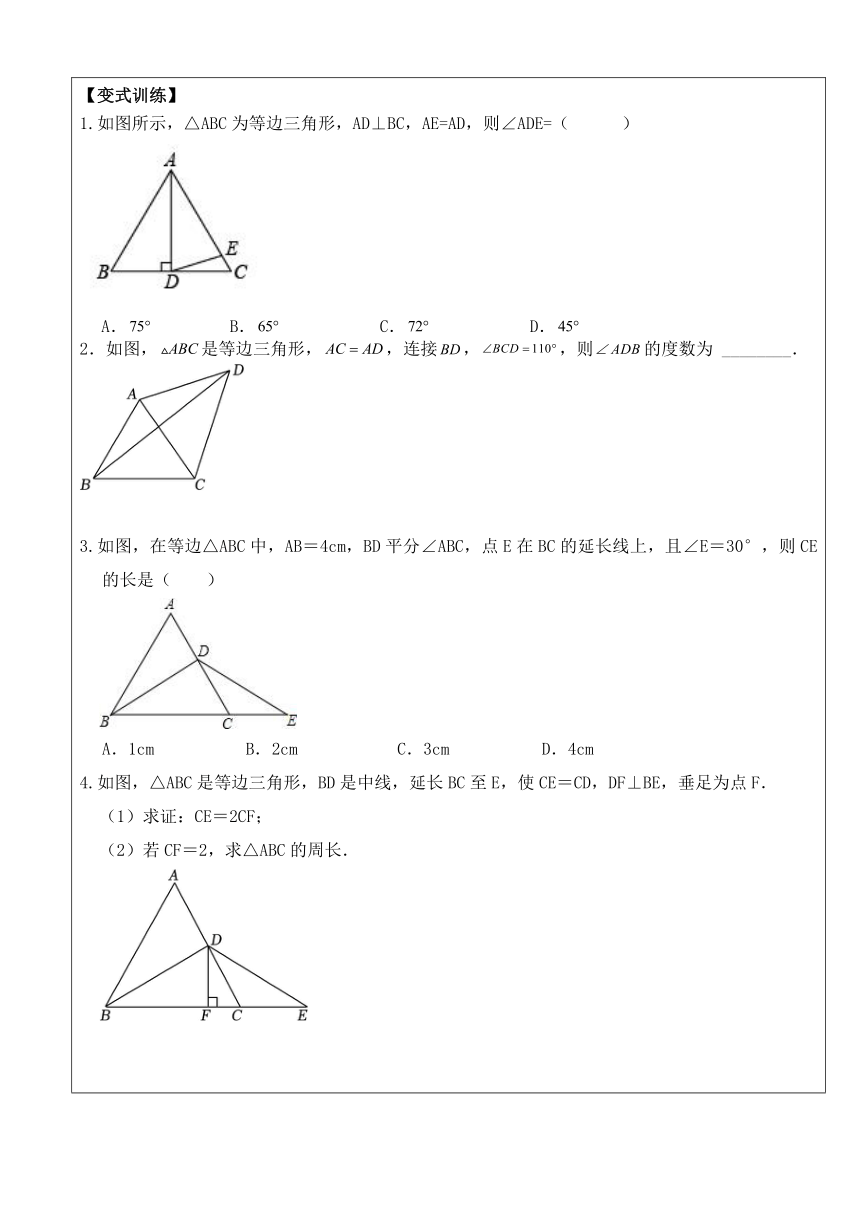
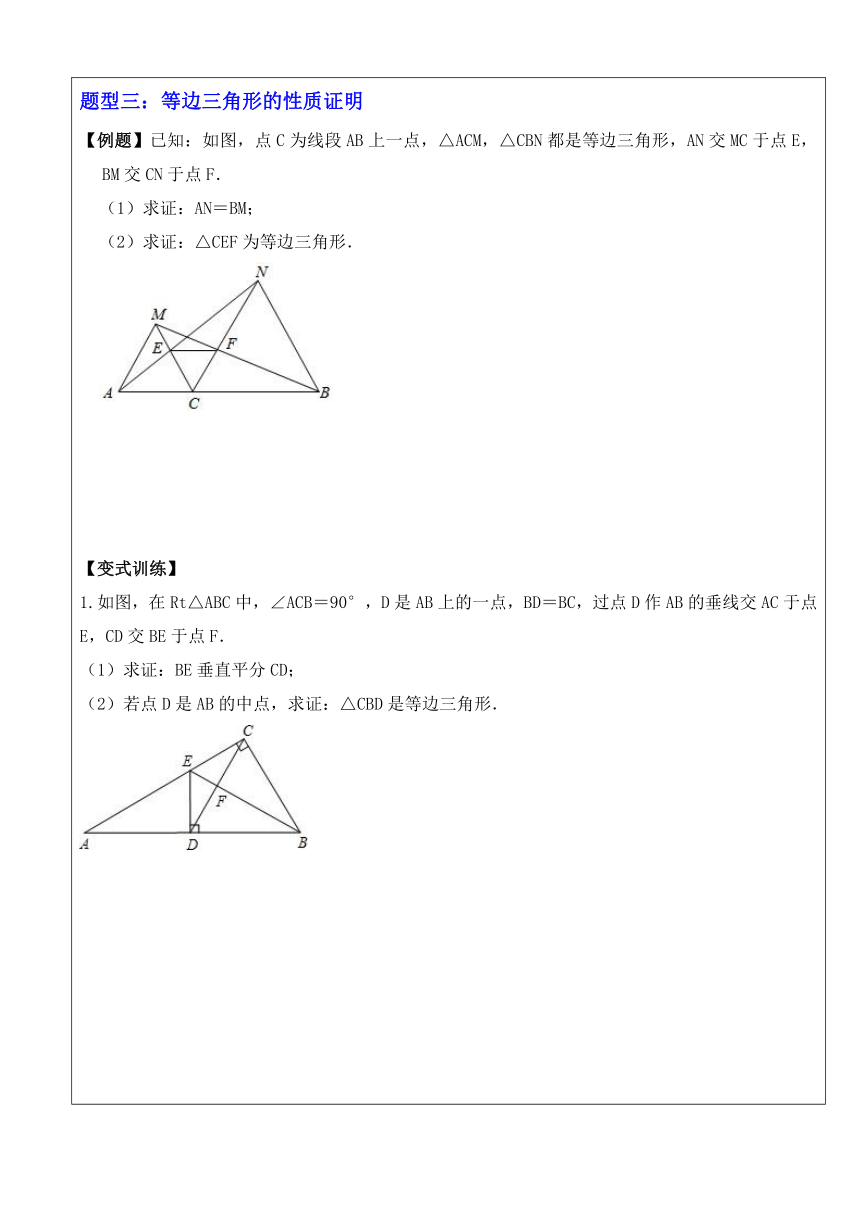
(1)三条边都相等的三角形是等边三角形; (2)三个角都相等的三角形是等边三角形; (3)有一个角是60°的等腰三角形是等边三角形. 【典型例题】 题型一:等边三角形的性质 【例题】如图,在△ABC中,D,E是边BC的三等分点,且△ADE是等边三角形,则∠BAC的度数为( ) A.105° B.120° C.130° D.150° 【变式训练】 1.如图所示,△ABC为等边三角形,AD⊥BC,AE=AD,则∠ADE=( ) A. B. C. D. 2.如图,是等边三角形,,连接,,则的度数为 ________. 3.如图,在等边△ABC中,AB=4cm,BD平分∠ABC,点E在BC的延长线上,且∠E=30°,则CE的长是( ) A.1cm B.2cm C.3cm D.4cm 4.如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD,DF⊥BE,垂足为点F. (1)求证:CE=2CF; (2)若CF=2,求△ABC的周长. 题型二:等边三角形的判定 【例题】若一个三角形有两条边相等,且有一内角为60°,那么这个三角形一定为( ) A.钝角三角形 B.等腰三角形 C.直角三角形 D.正三角形 【变式训练】 1.若一个三角形的最小内角为60°,则下列判断中正确的是( ) A.这个三角形是钝角三角形 B.这个三角形是直角三角形 C.这个三角形是等边三角形 D.不存在这样的三角形 2.下列说法不正确的是( ) A.有一个角为的三角形是等边三角形; B.三边相等的三角形是等边三角形 C.三个角相等的三角形是等边三角形 D.有一个角是的等腰三角形是等边三角形 3.在下列结论中: (1)有一个外角是的等腰三角形是等边三角形 (2)有两个外角相等的等腰三角形是等边三角形 (3)有一边上的高也是这边上的中线的等腰三角形是等边三角形 (4)三个外角都相等的三角形是等边三角形 其中正确的个数是( ) A.4个 B.3个 C.2个 D.1个 4.三角形的三边长a,b,c满足(a﹣b)4+(b﹣c)2+|c﹣a|=0,那么这个三角形一定是( ) A.直角三角形 B.等边三角形 C.等腰非等边三角形 D.钝角三角形 5.在边长为9的等边三角形ABC中,点Q是BC上一点,点P是AB上一动点,以每秒1个单位的速度从点A向点B移动,设运动时间为t秒. (1)如图1,若BQ=6,PQ∥AC,求t的值; (2)如图2,若点P从点A向点B运动,同时点Q以每秒2个单位的速度从点B经点C向点A运动,当t为何值时,△APQ为等边三角形? 题型三:等边三角形的性质证明 【例题】已知:如图,点C为线段AB上一点,△ACM,△CBN都是等边三角形,AN交MC于点E,BM交CN于点F. (1)求证:AN=BM; (2)求证:△CEF为等边三角形. 【变式训练】 1.如图,在Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC,过点D作AB的垂线交AC于点E,CD交BE于点F. (1)求证:BE垂直平分CD; (2)若点D是AB的中点,求证:△CBD是等边三角形. 2.如图,点O是等边内一点,以OC为边作等边三角形OCD,连接OD. (1)求证:; (2)若,,当为多少度时,是等腰三角形. 3.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点. (1)若∠BAC=60°,∠C=70°,求∠AFB的大小; (2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形. 4.如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC. (1)试判定△ODE的形状,并说明你的理由; (2)若BC=10,求△ODE的周长. 【过关检测】 选择题 1.在下列结论中: (1)有一个外角是120°的等腰三角形是等边三角形 (2)有两个外角相等的等腰三角形是等边三角形 (3)有一边上的高也是这边上的中线的等腰三角形是等边三角形 (4)三个外角都相等的三角形是等边三角形 其中正确的个数是( ) A.4个 B.3个 C.2个 D.1个 2.在解答一道习题时,嘉嘉先作出了的一条高,又作出了的一条角平分线,发现作的是同一条线段,则一定是( ) A.等腰直角三角形 B.直角三角形 C.等腰三角形 D.等边三角形 3.若一个等腰三角形腰上的高等于腰长的一半,则此等腰三角形的底角的度数是( ) A. B. C.或 D.无法确定 4.如图,直线m∥n,△ABC是等边三角形,顶点B在直线n上,直线m交AB于点E,交AC于点F,若∠1=140°,则∠2的度数是( ) A.80° B.100° C.120° D.140° 5.如图,中,,是中线,,将沿折叠至,则点C到的距离是( ) A.4 B. C.3 D. 6.如图,已知等边△AEB和等边△BDC在线段AC同侧,则下面错误的是( ) A.△ABD≌△EBC B.△NBC≌△MBD C.DM=DC D.∠ABD=∠EBC 7.如图,在中,,按图进行翻折,使,,则的度数是( ) A.25° B.30° C.35° D.40° 填空题 1.在△ABC中,∠A=60°,要使是等边三角形,则需要添加一条件是______. 2.如图,在等边△ABC中,于点D,若,则________. 3.如图,在△ABC中,BD平分∠ABC,如果AB=8,BC=12,△ABD的面积为16,则△CBD的面积为 _____. 4.如图,在△ABC中,P,Q分别是BC,AC上的点,PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,那么下面四个结论:①AS=AR:②QPAR;③△BRP≌△QSP:④BR=QS,其中一定正确的是(填写编号)________. 5.如图,∠EAB=∠CAF,AE=AB,∠E=∠B,给出下列结论:①EF=BC;②AD=AC;③;④∠CAF=∠BFE;⑤AF是∠EFC的平分线.其中正确的结论有_____.(填写序号) 解答题 1.等边中,,且. (1)求证:. (2)求的度数. 2.如图,△ABC和△ADE都是等边三角形,点B在ED的延长线上. (1)求证:△ABD≌△ACE; (2)若AE=2,CE=3,求BE的长; (3)求∠BEC的度数 3.如图,已知是边长为的等边三角形,动点P从A点出发,以的速度向B运动,同时点Q从B点出发以速度向C运动,当Q点到达点时,两点停止运动.设点P的运动时间为t(),则 (1) ___________, ___________;(用含t的代数式表示) (2)当t为何值时,是等边三角形? (3)当t为何值时,是直角三角形?
4.在等边三角形中,D为射线上一点,连接,点B关于直线的对称点为E,连接. (1)如图1,点D在线段上,,求的度数; (2)射线与射线的交于点F,过点D作交射线于点G,连接交于点H. ①如图2,点D在线段上,求证:; ②点D在线段延长线上,用等式表示线段和之间的数量关系,并说明理由.
知识梳理 【知识点1】等边三角形 等边三角形定义:三边都相等的三角形叫等边三角形. 特别说明:由定义可知,等边三角形是一种特殊的等腰三角形.也就是说等腰三角形包括等边三角形. 等边三角形的性质:等边三角形三个内角都相等,并且每一个内角都等于60°. 等边三角形的轴对称性:有3条对称轴,即3条高所在的直线或3条中线所在的直线或3条角平分线所在的直线。 等边三角形的判定:
(1)三条边都相等的三角形是等边三角形; (2)三个角都相等的三角形是等边三角形; (3)有一个角是60°的等腰三角形是等边三角形. 【典型例题】 题型一:等边三角形的性质 【例题】如图,在△ABC中,D,E是边BC的三等分点,且△ADE是等边三角形,则∠BAC的度数为( ) A.105° B.120° C.130° D.150° 【变式训练】 1.如图所示,△ABC为等边三角形,AD⊥BC,AE=AD,则∠ADE=( ) A. B. C. D. 2.如图,是等边三角形,,连接,,则的度数为 ________. 3.如图,在等边△ABC中,AB=4cm,BD平分∠ABC,点E在BC的延长线上,且∠E=30°,则CE的长是( ) A.1cm B.2cm C.3cm D.4cm 4.如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD,DF⊥BE,垂足为点F. (1)求证:CE=2CF; (2)若CF=2,求△ABC的周长. 题型二:等边三角形的判定 【例题】若一个三角形有两条边相等,且有一内角为60°,那么这个三角形一定为( ) A.钝角三角形 B.等腰三角形 C.直角三角形 D.正三角形 【变式训练】 1.若一个三角形的最小内角为60°,则下列判断中正确的是( ) A.这个三角形是钝角三角形 B.这个三角形是直角三角形 C.这个三角形是等边三角形 D.不存在这样的三角形 2.下列说法不正确的是( ) A.有一个角为的三角形是等边三角形; B.三边相等的三角形是等边三角形 C.三个角相等的三角形是等边三角形 D.有一个角是的等腰三角形是等边三角形 3.在下列结论中: (1)有一个外角是的等腰三角形是等边三角形 (2)有两个外角相等的等腰三角形是等边三角形 (3)有一边上的高也是这边上的中线的等腰三角形是等边三角形 (4)三个外角都相等的三角形是等边三角形 其中正确的个数是( ) A.4个 B.3个 C.2个 D.1个 4.三角形的三边长a,b,c满足(a﹣b)4+(b﹣c)2+|c﹣a|=0,那么这个三角形一定是( ) A.直角三角形 B.等边三角形 C.等腰非等边三角形 D.钝角三角形 5.在边长为9的等边三角形ABC中,点Q是BC上一点,点P是AB上一动点,以每秒1个单位的速度从点A向点B移动,设运动时间为t秒. (1)如图1,若BQ=6,PQ∥AC,求t的值; (2)如图2,若点P从点A向点B运动,同时点Q以每秒2个单位的速度从点B经点C向点A运动,当t为何值时,△APQ为等边三角形? 题型三:等边三角形的性质证明 【例题】已知:如图,点C为线段AB上一点,△ACM,△CBN都是等边三角形,AN交MC于点E,BM交CN于点F. (1)求证:AN=BM; (2)求证:△CEF为等边三角形. 【变式训练】 1.如图,在Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC,过点D作AB的垂线交AC于点E,CD交BE于点F. (1)求证:BE垂直平分CD; (2)若点D是AB的中点,求证:△CBD是等边三角形. 2.如图,点O是等边内一点,以OC为边作等边三角形OCD,连接OD. (1)求证:; (2)若,,当为多少度时,是等腰三角形. 3.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点. (1)若∠BAC=60°,∠C=70°,求∠AFB的大小; (2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形. 4.如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC. (1)试判定△ODE的形状,并说明你的理由; (2)若BC=10,求△ODE的周长. 【过关检测】 选择题 1.在下列结论中: (1)有一个外角是120°的等腰三角形是等边三角形 (2)有两个外角相等的等腰三角形是等边三角形 (3)有一边上的高也是这边上的中线的等腰三角形是等边三角形 (4)三个外角都相等的三角形是等边三角形 其中正确的个数是( ) A.4个 B.3个 C.2个 D.1个 2.在解答一道习题时,嘉嘉先作出了的一条高,又作出了的一条角平分线,发现作的是同一条线段,则一定是( ) A.等腰直角三角形 B.直角三角形 C.等腰三角形 D.等边三角形 3.若一个等腰三角形腰上的高等于腰长的一半,则此等腰三角形的底角的度数是( ) A. B. C.或 D.无法确定 4.如图,直线m∥n,△ABC是等边三角形,顶点B在直线n上,直线m交AB于点E,交AC于点F,若∠1=140°,则∠2的度数是( ) A.80° B.100° C.120° D.140° 5.如图,中,,是中线,,将沿折叠至,则点C到的距离是( ) A.4 B. C.3 D. 6.如图,已知等边△AEB和等边△BDC在线段AC同侧,则下面错误的是( ) A.△ABD≌△EBC B.△NBC≌△MBD C.DM=DC D.∠ABD=∠EBC 7.如图,在中,,按图进行翻折,使,,则的度数是( ) A.25° B.30° C.35° D.40° 填空题 1.在△ABC中,∠A=60°,要使是等边三角形,则需要添加一条件是______. 2.如图,在等边△ABC中,于点D,若,则________. 3.如图,在△ABC中,BD平分∠ABC,如果AB=8,BC=12,△ABD的面积为16,则△CBD的面积为 _____. 4.如图,在△ABC中,P,Q分别是BC,AC上的点,PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,那么下面四个结论:①AS=AR:②QPAR;③△BRP≌△QSP:④BR=QS,其中一定正确的是(填写编号)________. 5.如图,∠EAB=∠CAF,AE=AB,∠E=∠B,给出下列结论:①EF=BC;②AD=AC;③;④∠CAF=∠BFE;⑤AF是∠EFC的平分线.其中正确的结论有_____.(填写序号) 解答题 1.等边中,,且. (1)求证:. (2)求的度数. 2.如图,△ABC和△ADE都是等边三角形,点B在ED的延长线上. (1)求证:△ABD≌△ACE; (2)若AE=2,CE=3,求BE的长; (3)求∠BEC的度数 3.如图,已知是边长为的等边三角形,动点P从A点出发,以的速度向B运动,同时点Q从B点出发以速度向C运动,当Q点到达点时,两点停止运动.设点P的运动时间为t(),则 (1) ___________, ___________;(用含t的代数式表示) (2)当t为何值时,是等边三角形? (3)当t为何值时,是直角三角形?
4.在等边三角形中,D为射线上一点,连接,点B关于直线的对称点为E,连接. (1)如图1,点D在线段上,,求的度数; (2)射线与射线的交于点F,过点D作交射线于点G,连接交于点H. ①如图2,点D在线段上,求证:; ②点D在线段延长线上,用等式表示线段和之间的数量关系,并说明理由.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
