第七章平面直角坐标系单元复习题 人教版七年级数学下册(含解析)
文档属性
| 名称 | 第七章平面直角坐标系单元复习题 人教版七年级数学下册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 272.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 16:25:47 | ||
图片预览



文档简介
人教版七年级数学下册第七章平面直角坐标系单元复习题
一、选择题
1.如果用有序数对(3,2)表示教室里第3列第2排的座位,则位于第5列第4排的座位应记作( )
A.(4,5) B.(5,4) C.(3,2) D.(2,3)
2.在平面直角坐标系中,所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.广州,美丽的羊城,没有冬季严寒,是热门旅游城市之一,经济发达,历史人文底蕴深厚.下列表示广州市地理位置最合理的是( )
A.在中国南部 B.毗邻港滨
C.距离北京2000公里 D.东经、北纬
4.点先向左平移3个单位,再向上平移2个单位,得到对应点的坐标为( )
A. B. C. D.
5.课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成( )
A.(5,4) B.(4,4) C.(3,4) D.(4,3)
6.如果点在平面直角坐标系中的第四象限内,则下列不等式中正确的是( )
A. B. C. D.
7.已知,若在第四象限,则的值为( )
A.9 B. C.1 D.
8.如图,用方向和距离描述图书馆相对于小青家的位置是()
A.北偏东,3km B.北偏东,3km
C.东偏北 D.东偏北,3km
9.已知点A(﹣2,4),将点A往上平移2个单位长度,再往左平移3个单位长度得到点A′,则点A′的坐标是( )
A.(﹣5,6) B.(1,2) C.(1,6) D.(﹣5,2)
10.若点A(3,5),轴,且AB=2,则B点坐标为( )
A.(3,3) B.(1,5)或(5,5)
C.(5,5) D.(3,3)或(3,7)
二、填空题
11.如果小明的座位是3组8号,记作(3,8),那么记作(2,4)表示的座位是 .
12.在平面直角坐标系中,已知点在轴上,则点的坐标为 .
13.如图,货船A与港口B相距30海里,我们用有序数对(南偏西,30海里)来描述港口B相对货船A的位置,那么货船A相对港口B的位置可描述为 .
14.在平面直角坐标系内,线段平行于轴,且,若点的坐标为,则点的坐标是 .
三、解答题
15.如图,正方形网格中的交点,我们称之为格点,点A用有序数对(2,2)表示,其中第一个数表示排数,第2个数表示列数,在图中有一个格点C,使S△ABC=1,写出符合条件的点C的有序数对.
16.如果点B 到x轴的距离与它到y轴的距离相等,求点B的坐标.
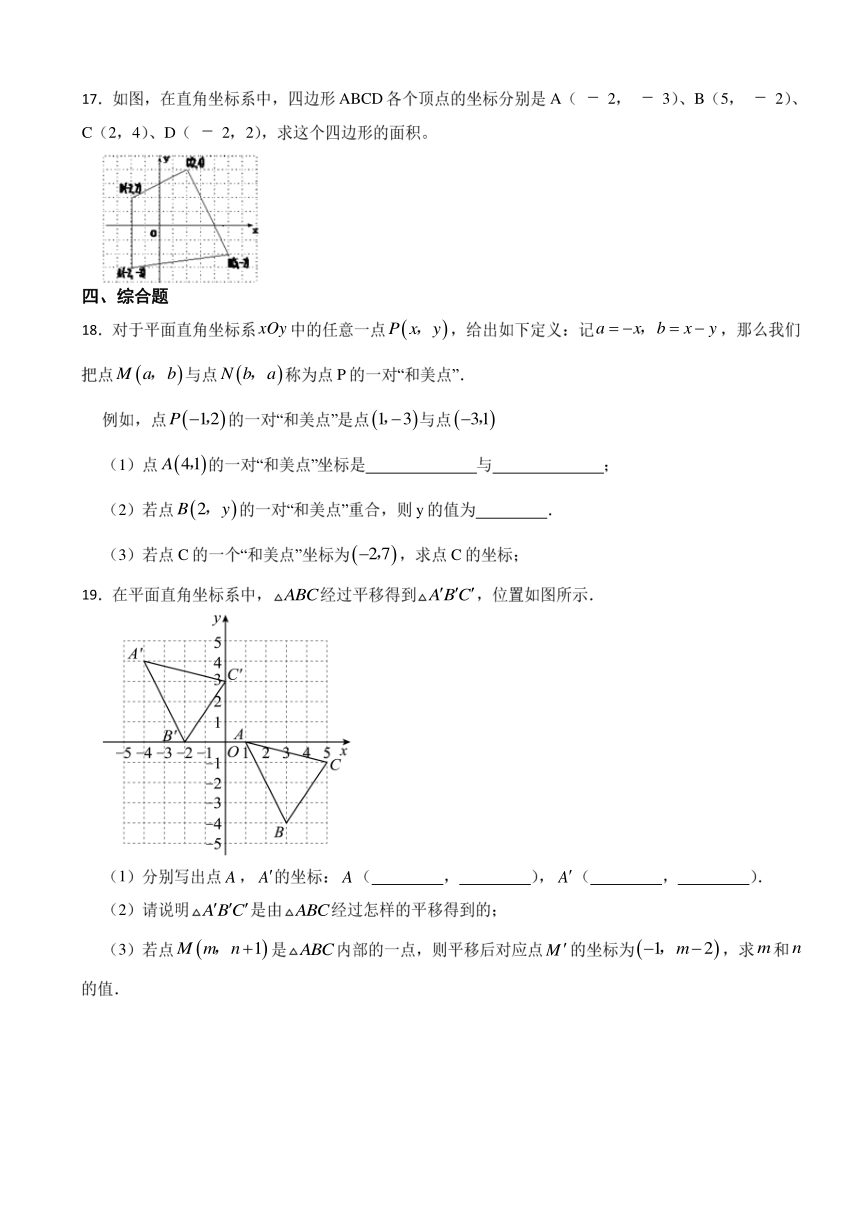
17.如图,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A( 2, 3)、B(5, 2)、C(2,4)、D( 2,2),求这个四边形的面积。
四、综合题
18.对于平面直角坐标系中的任意一点,给出如下定义:记,那么我们把点与点称为点P的一对“和美点”.
例如,点的一对“和美点”是点与点
(1)点的一对“和美点”坐标是 与 ;
(2)若点的一对“和美点”重合,则y的值为 .
(3)若点C的一个“和美点”坐标为,求点C的坐标;
19.在平面直角坐标系中,经过平移得到,位置如图所示.
(1)分别写出点,的坐标:( , ),( , ).
(2)请说明是由经过怎样的平移得到的;
(3)若点是内部的一点,则平移后对应点的坐标为,求和的值.
答案解析部分
1.【答案】B
【解析】【解答】解:∵ 表示教室里第 列第 排的座位
∴第 列第 排的座位应记作 .
故答案为:B
【分析】由题意知:第一个数表述列数,第二个数表示排数,据此写出结论即可.
2.【答案】D
【解析】【解答】解:∵点(3,-4)的横坐标为负数,纵坐标为正数,
∴(3,-4)所在的象限为第四象限.
故答案为:D.
【分析】若A(m,n),当m>0,n>0时,点A在第一象限;当m<0,n>0时,点A在第二象限;当m<0,n<0时,点A在第三象限;当m>0,n<0时,点A在第四象限.
3.【答案】D
【解析】【解答】解: 表示广州市地理位置最合理的是东经113°,北纬23°.
故答案为:D
【分析】根据在地理上采用经纬度来表示某个点的位置,既有经度又有纬度,据此可得答案.
4.【答案】B
【解析】【解答】解:向左平移3个单位后的坐标为(0,2)。再向上平移2个单位后的坐标为(0,4)
故答案为:
【分析】点的坐标左右平移时纵坐标不变,上下平移时横坐标不变。
5.【答案】B
【解析】【解答】建立如图所示的平面直角坐标系:
小慧的位置可表示为(4,4)。
故答案为:B
【分析】先先建立直角坐标系,然后写出小慧所在位置所对应点的坐标即可。
6.【答案】C
【解析】【解答】解:由题意可得:m>0,n<0
A:mn<0,A错误
B:,,B错误
D:,,D错误
故答案为:D
【分析】根据第四象限点的坐标特征即可求出答案。
7.【答案】D
【解析】【解答】解:∵,
∴m=4或-4,n=5或-5,
∵在第四象限 ,
∴m>0,n<0,
∴m=4,n=-5,
∴m+n=-1;
故答案为:D.
【分析】根据平方根及绝对值的性质可得m=4或-4,n=5或-5,再利用第四象限内点的符号为正、负,可确定m=4,n=-5,然后代入计算即可.
8.【答案】B
【解析】【解答】解:如图,
,
图书馆的位置在小青家的东偏北方向或北偏东方向,
,
图书馆的位置到小青家的距离为3km,
图书馆的位置在小青家东偏北(北偏东)3km处.
故答案为:B.
【分析】根据图象中的角度可知图书馆的位置在小青家的东偏北方向或北偏东方向,再由线段OA的长度可知图书馆的位置到小青家的距离为3km,故可得到图书馆的位置在小青家东偏北(北偏东)3km处.
9.【答案】A
【解析】【解答】解:点A 往上平移2个单位长度,再往左平移3个单位长度后,点的坐标为(-2-3,4+2),
即A′(-5,6),
故答案为:A.
【分析】根据平移的性质求点的坐标即可。
10.【答案】D
【解析】【解答】解:如图所示:
∵轴,
∴点B的横坐标与点A的横坐标相同,
∵AB=2,
∴点B在A点上方时,坐标为(3,7),点B在A点下方时,坐标为(3,3),
综上分析可知,B点坐标为(3,3)或(3,7),故D符合题意.
故答案为:D.
【分析】由轴,可得点B的横坐标与点A的横坐标相同,由AB=2,分两种情况:点B在A点上方时和点B在A点下方时,据此分别解答即可.
11.【答案】2组4号
【解析】【解答】解:小明的座位是3组8号,记作(3,8),
则(2,4)表示2组4号.
故答案为:2组4号.
【分析】参照题干中的定义及书写要求求解即可。
12.【答案】
【解析】【解答】解: 点在轴上,
,
,
点的坐标为 .
故答案为:.
【分析】x轴上点的纵坐标为零,以此可求得m的值,进而得到点M的坐标.
13.【答案】(北偏东,30海里)
【解析】【解答】解:由图可知,A在B北偏东方向上
货船A相对港口B的位置可描述为(北偏东,30海里)
故答案为:(北偏东,30海里)
【分析】由图可知,A在B北偏东方向上,距离不变即可求出答案。
14.【答案】或
【解析】【解答】解:∵AB∥x轴,B(2,4),
∴点A的纵坐标为4,
∵AB=3,∴点A的横坐标为2-3=-1,2+3=5,
∴B(5,4)或(-1,4);
故答案为:(5,4)或(-1,4).
【分析】由AB∥x轴可知点A与点B的纵坐标相同,由AB=3,可知点B在点A的左侧或右侧,据此解答即可.
15.【答案】解:如图,点C可以为(1,3),(5,3),(2,4),(3,1),(3,5),(4,2).
【解析】【分析】根据A、B点间的水平距离和竖直距离都是1,找出使AC或BC为2的点C即可.
16.【答案】解:根据题意得,m-1=3m+5或m-1=-(3m+5),
解m-1=3m+5,得m=-3,
∴m-1=-4,点B的坐标为(-4,-4),
解m-1=-(3m+5),得m=-1,
∴m-1=-2,点B的坐标为(-2,2),
∴点B的坐标为(-4,-4)或(-2,2).
【解析】【分析】根据点B 到x轴的距离与它到y轴的距离相等,坐标平面内的点到两轴的距离实际上就是该点两坐标的绝对值即可得出答案.
17.【答案】解:过C点作x轴的平行线,与AD的延长线交于F,作BE⊥CF,交FC的延长线于E,
根据点的坐标可知,AF=7,DF=2,EF=7,CE=3,CF=4,BE=6,
∴S四边形ABCD=S梯形BEFA-S△BEC-S△CDF
= (6+7)×7- ×3×6- ×2×4
=32.5
【解析】【分析】采用割补法, 过C点作x轴的平行线,与AD的延长线交于F,作BE⊥CF,交FC的延长线于E,由S四边形ABCD=S梯形BEFA-S△BEC-S△CDF,利用梯形的面积公式及三角形的面积公式即得.
18.【答案】(1)(-4,3);(3,-4)
(2)4
(3)解:当和美点坐标(a,b)为(-2,7),
则a=-x=-2,x=2,
b=x-y=7,y=-5,
∴C(2,-5);
当和美点坐标(b,a)为(-2,7),
b=x-y=-2,a=-x=7,
∴x=-7,y=-5,
∴C(-7,-5).
综上所述,C(2,-5)或C(-7,-5).
【解析】【解答】解:(1)由题意得点的一对“和美点”坐标是(-4,3)与(3,-4),
故答案:(-4,3),(3,-4),
(2)∵点的一对“和美点”重合,
∴点的“和美点”为(2,2),
∴y=4,
故答案为:4
【分析】(1)根据“和美点”的定义即可直接求解;
(2)根据题意即可得到点的“和美点”为(2,2),进而即可求解;
(3)先根据题意分类讨论即可得到点C的坐标。
19.【答案】(1)1;0;-4;4
(2)解:由坐标可知,是由向左平移个单位,向上平移个单位得到;
(3)解:
由题意,,
解得:
∴,.
【解析】【解答】解:(1)观察图形可知A的坐标为(1,0), A' 的坐标为(-4,4).
故答案为:1;0;-4;4;
【分析】(1)根据点的位置写出坐标即可;
(2)利用平移变换的性质判断即可;
(3)利用平移变换的性质,构建方程组求解.
一、选择题
1.如果用有序数对(3,2)表示教室里第3列第2排的座位,则位于第5列第4排的座位应记作( )
A.(4,5) B.(5,4) C.(3,2) D.(2,3)
2.在平面直角坐标系中,所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.广州,美丽的羊城,没有冬季严寒,是热门旅游城市之一,经济发达,历史人文底蕴深厚.下列表示广州市地理位置最合理的是( )
A.在中国南部 B.毗邻港滨
C.距离北京2000公里 D.东经、北纬
4.点先向左平移3个单位,再向上平移2个单位,得到对应点的坐标为( )
A. B. C. D.
5.课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成( )
A.(5,4) B.(4,4) C.(3,4) D.(4,3)
6.如果点在平面直角坐标系中的第四象限内,则下列不等式中正确的是( )
A. B. C. D.
7.已知,若在第四象限,则的值为( )
A.9 B. C.1 D.
8.如图,用方向和距离描述图书馆相对于小青家的位置是()
A.北偏东,3km B.北偏东,3km
C.东偏北 D.东偏北,3km
9.已知点A(﹣2,4),将点A往上平移2个单位长度,再往左平移3个单位长度得到点A′,则点A′的坐标是( )
A.(﹣5,6) B.(1,2) C.(1,6) D.(﹣5,2)
10.若点A(3,5),轴,且AB=2,则B点坐标为( )
A.(3,3) B.(1,5)或(5,5)
C.(5,5) D.(3,3)或(3,7)
二、填空题
11.如果小明的座位是3组8号,记作(3,8),那么记作(2,4)表示的座位是 .
12.在平面直角坐标系中,已知点在轴上,则点的坐标为 .
13.如图,货船A与港口B相距30海里,我们用有序数对(南偏西,30海里)来描述港口B相对货船A的位置,那么货船A相对港口B的位置可描述为 .
14.在平面直角坐标系内,线段平行于轴,且,若点的坐标为,则点的坐标是 .
三、解答题
15.如图,正方形网格中的交点,我们称之为格点,点A用有序数对(2,2)表示,其中第一个数表示排数,第2个数表示列数,在图中有一个格点C,使S△ABC=1,写出符合条件的点C的有序数对.
16.如果点B 到x轴的距离与它到y轴的距离相等,求点B的坐标.
17.如图,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A( 2, 3)、B(5, 2)、C(2,4)、D( 2,2),求这个四边形的面积。
四、综合题
18.对于平面直角坐标系中的任意一点,给出如下定义:记,那么我们把点与点称为点P的一对“和美点”.
例如,点的一对“和美点”是点与点
(1)点的一对“和美点”坐标是 与 ;
(2)若点的一对“和美点”重合,则y的值为 .
(3)若点C的一个“和美点”坐标为,求点C的坐标;
19.在平面直角坐标系中,经过平移得到,位置如图所示.
(1)分别写出点,的坐标:( , ),( , ).
(2)请说明是由经过怎样的平移得到的;
(3)若点是内部的一点,则平移后对应点的坐标为,求和的值.
答案解析部分
1.【答案】B
【解析】【解答】解:∵ 表示教室里第 列第 排的座位
∴第 列第 排的座位应记作 .
故答案为:B
【分析】由题意知:第一个数表述列数,第二个数表示排数,据此写出结论即可.
2.【答案】D
【解析】【解答】解:∵点(3,-4)的横坐标为负数,纵坐标为正数,
∴(3,-4)所在的象限为第四象限.
故答案为:D.
【分析】若A(m,n),当m>0,n>0时,点A在第一象限;当m<0,n>0时,点A在第二象限;当m<0,n<0时,点A在第三象限;当m>0,n<0时,点A在第四象限.
3.【答案】D
【解析】【解答】解: 表示广州市地理位置最合理的是东经113°,北纬23°.
故答案为:D
【分析】根据在地理上采用经纬度来表示某个点的位置,既有经度又有纬度,据此可得答案.
4.【答案】B
【解析】【解答】解:向左平移3个单位后的坐标为(0,2)。再向上平移2个单位后的坐标为(0,4)
故答案为:
【分析】点的坐标左右平移时纵坐标不变,上下平移时横坐标不变。
5.【答案】B
【解析】【解答】建立如图所示的平面直角坐标系:
小慧的位置可表示为(4,4)。
故答案为:B
【分析】先先建立直角坐标系,然后写出小慧所在位置所对应点的坐标即可。
6.【答案】C
【解析】【解答】解:由题意可得:m>0,n<0
A:mn<0,A错误
B:,,B错误
D:,,D错误
故答案为:D
【分析】根据第四象限点的坐标特征即可求出答案。
7.【答案】D
【解析】【解答】解:∵,
∴m=4或-4,n=5或-5,
∵在第四象限 ,
∴m>0,n<0,
∴m=4,n=-5,
∴m+n=-1;
故答案为:D.
【分析】根据平方根及绝对值的性质可得m=4或-4,n=5或-5,再利用第四象限内点的符号为正、负,可确定m=4,n=-5,然后代入计算即可.
8.【答案】B
【解析】【解答】解:如图,
,
图书馆的位置在小青家的东偏北方向或北偏东方向,
,
图书馆的位置到小青家的距离为3km,
图书馆的位置在小青家东偏北(北偏东)3km处.
故答案为:B.
【分析】根据图象中的角度可知图书馆的位置在小青家的东偏北方向或北偏东方向,再由线段OA的长度可知图书馆的位置到小青家的距离为3km,故可得到图书馆的位置在小青家东偏北(北偏东)3km处.
9.【答案】A
【解析】【解答】解:点A 往上平移2个单位长度,再往左平移3个单位长度后,点的坐标为(-2-3,4+2),
即A′(-5,6),
故答案为:A.
【分析】根据平移的性质求点的坐标即可。
10.【答案】D
【解析】【解答】解:如图所示:
∵轴,
∴点B的横坐标与点A的横坐标相同,
∵AB=2,
∴点B在A点上方时,坐标为(3,7),点B在A点下方时,坐标为(3,3),
综上分析可知,B点坐标为(3,3)或(3,7),故D符合题意.
故答案为:D.
【分析】由轴,可得点B的横坐标与点A的横坐标相同,由AB=2,分两种情况:点B在A点上方时和点B在A点下方时,据此分别解答即可.
11.【答案】2组4号
【解析】【解答】解:小明的座位是3组8号,记作(3,8),
则(2,4)表示2组4号.
故答案为:2组4号.
【分析】参照题干中的定义及书写要求求解即可。
12.【答案】
【解析】【解答】解: 点在轴上,
,
,
点的坐标为 .
故答案为:.
【分析】x轴上点的纵坐标为零,以此可求得m的值,进而得到点M的坐标.
13.【答案】(北偏东,30海里)
【解析】【解答】解:由图可知,A在B北偏东方向上
货船A相对港口B的位置可描述为(北偏东,30海里)
故答案为:(北偏东,30海里)
【分析】由图可知,A在B北偏东方向上,距离不变即可求出答案。
14.【答案】或
【解析】【解答】解:∵AB∥x轴,B(2,4),
∴点A的纵坐标为4,
∵AB=3,∴点A的横坐标为2-3=-1,2+3=5,
∴B(5,4)或(-1,4);
故答案为:(5,4)或(-1,4).
【分析】由AB∥x轴可知点A与点B的纵坐标相同,由AB=3,可知点B在点A的左侧或右侧,据此解答即可.
15.【答案】解:如图,点C可以为(1,3),(5,3),(2,4),(3,1),(3,5),(4,2).
【解析】【分析】根据A、B点间的水平距离和竖直距离都是1,找出使AC或BC为2的点C即可.
16.【答案】解:根据题意得,m-1=3m+5或m-1=-(3m+5),
解m-1=3m+5,得m=-3,
∴m-1=-4,点B的坐标为(-4,-4),
解m-1=-(3m+5),得m=-1,
∴m-1=-2,点B的坐标为(-2,2),
∴点B的坐标为(-4,-4)或(-2,2).
【解析】【分析】根据点B 到x轴的距离与它到y轴的距离相等,坐标平面内的点到两轴的距离实际上就是该点两坐标的绝对值即可得出答案.
17.【答案】解:过C点作x轴的平行线,与AD的延长线交于F,作BE⊥CF,交FC的延长线于E,
根据点的坐标可知,AF=7,DF=2,EF=7,CE=3,CF=4,BE=6,
∴S四边形ABCD=S梯形BEFA-S△BEC-S△CDF
= (6+7)×7- ×3×6- ×2×4
=32.5
【解析】【分析】采用割补法, 过C点作x轴的平行线,与AD的延长线交于F,作BE⊥CF,交FC的延长线于E,由S四边形ABCD=S梯形BEFA-S△BEC-S△CDF,利用梯形的面积公式及三角形的面积公式即得.
18.【答案】(1)(-4,3);(3,-4)
(2)4
(3)解:当和美点坐标(a,b)为(-2,7),
则a=-x=-2,x=2,
b=x-y=7,y=-5,
∴C(2,-5);
当和美点坐标(b,a)为(-2,7),
b=x-y=-2,a=-x=7,
∴x=-7,y=-5,
∴C(-7,-5).
综上所述,C(2,-5)或C(-7,-5).
【解析】【解答】解:(1)由题意得点的一对“和美点”坐标是(-4,3)与(3,-4),
故答案:(-4,3),(3,-4),
(2)∵点的一对“和美点”重合,
∴点的“和美点”为(2,2),
∴y=4,
故答案为:4
【分析】(1)根据“和美点”的定义即可直接求解;
(2)根据题意即可得到点的“和美点”为(2,2),进而即可求解;
(3)先根据题意分类讨论即可得到点C的坐标。
19.【答案】(1)1;0;-4;4
(2)解:由坐标可知,是由向左平移个单位,向上平移个单位得到;
(3)解:
由题意,,
解得:
∴,.
【解析】【解答】解:(1)观察图形可知A的坐标为(1,0), A' 的坐标为(-4,4).
故答案为:1;0;-4;4;
【分析】(1)根据点的位置写出坐标即可;
(2)利用平移变换的性质判断即可;
(3)利用平移变换的性质,构建方程组求解.
