解方程人教版五年级上册数学课件(共22张ppt)
文档属性
| 名称 | 解方程人教版五年级上册数学课件(共22张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-17 14:41:07 | ||
图片预览








文档简介
(共22张PPT)
解方程
简要提示
1.初步了解‘‘方程的解”和‘‘解方程”的意义。 2. 会解答简易方程。
3.会检验一个具体的值是不是方程的
解,掌握检验的格式。
重点和难点
比较方程的解和解方程这两个概念的含义
复习导入
1.4x=9.8 ( )
√
3x-8y=14 ( )
16+y<30 ( )
问题:下面哪个式子是方程?并说说理由。
下面哪个式子是方程?
×
21÷7=3 ( )
√
×
3x + 4 = 21 ○( )
3x - 8 = 21 ○( )
2、填空
已知 3x=21
3x × a = 21 ○( )
3x ○( )=21 ÷ b (b≠0)
+
4
—
8
×
a
÷
b
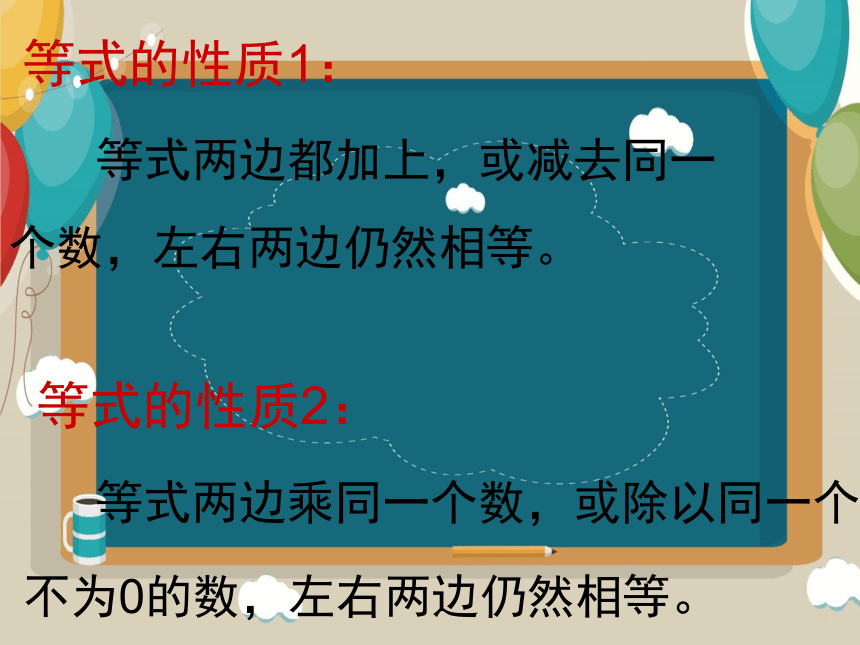
等式的性质2:
等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
等式的性质1:
等式两边都加上,或减去同一个数,左右两边仍然相等。
100g
100g
100g
50g
100+x=250
平衡
空杯子重100g,
水重x克。
X=?
100+x
100g
100g
100g
50g
平衡
100+x=250
X=?
100+150=250,
所以x=150。
100+x=100+150
假如两边同时减去100,就能得出x=150。
100+x=250
x=150
求方程的解的过程叫做解方程。
使方程左右两边相等的未知数的值,叫做
方程的解。
像上面,x=150就是方程100+x=250的解。
“方程的解”是指未知数的值,它是
一个数
“解方程”是求未知数X的值的
计算过程
我是这样理解解方程和方程的解的:
自主探究,构建新知
看图列方程,并求出方程的解。
①3x+4=40
②40-3x=4
③3x=40-4
汇报交流,发现总结
① 3x+4=40
解:3x+4-4=40-4
3x=36
x=12
3x÷3=36÷3
汇报交流,发现总结
② 40-3x=4
解:40-3x+3x=4+3x
40=4+3x
4+3x=40
3x=36
4+3x-4=40-4
x=12
3x÷3=36÷3
汇报交流,发现总结
3x+4=40
方程左边=3x+4
=3×12+4
=36+4
=方程右边
所以,x =12是方程的解。
=40
方法迁移,学会应用
解方程 2(x-16)=8
请你自己把这个方程解完。
方法迁移,学会应用
2(x-16)=8
方程左边=2(x-16)
=2×(20-16)
=2×4
=方程右边
所以,x=20是方程的解。
别忘了检验!
=8
看图列方程并求解。
x+3x=80
解: 4x=80
4x÷4=80÷4
x=20
方法迁移,学会应用
1.在解较复杂的方程时,可以把一个式子看作一个整体来解,然后利用等式的性质将复杂的方程转化成简单的方程。
2.在解方程时,也可以运用运算定律来解。
总结方法
1. 解方程。
6x-35=13
3x-42×6=6
巩固练习,提升认识
问题:1. 观察这个方程有几步运算?可以先把什么看做一个整体?
2. 请你独立思考并在纸上完成。
问题:1. 你能说说他们的想法吗?分别把什么看做一个整体?分几
大步解决?依据是什么?
巩固练习,提升认识
6x=48
解: 6x-35+35=13+35
6x-35=13
6x÷6=48÷6
x=8
3x-252+252=6+252
解: 3x-252=6
3x-42×6=6
3x=258
3x÷3=258÷3
x=86
2. 请你检验一下。
1. 解方程。
小结:在解两步、三步方程时,你有什么感悟?和大家分享一下。
巩固练习,提升认识
2. 看图列方程并求解。
问题:1. 你能根据图意列出方程吗?
2. 这个方程有几步运算?怎样解?把过程写下来。
3. 请你检验一下x=49是不是方程的解。
2x+30×2=158
方程左边=2x+30×2
=2×49+30×2
=98+60
=158
=方程右边
所以,x=49是方程的解。
解: 2x+60=158
2x+60-60=158-60
2x=98
2x÷2=98÷2
x=49
方程4.6+X=7.5和a-X=8.3中的X的值相同,求a的值是多少?
拓展训练:
4.6 +X= 7.5
解:4.6+X-4.6= 7.5-4.6
X = 2.9
a - 2.9 = 8.3
解:a - 2.9 +2.9= 8.3+2.9
a= 11.2
通过这节课的学习,
你有哪些收获
解方程
简要提示
1.初步了解‘‘方程的解”和‘‘解方程”的意义。 2. 会解答简易方程。
3.会检验一个具体的值是不是方程的
解,掌握检验的格式。
重点和难点
比较方程的解和解方程这两个概念的含义
复习导入
1.4x=9.8 ( )
√
3x-8y=14 ( )
16+y<30 ( )
问题:下面哪个式子是方程?并说说理由。
下面哪个式子是方程?
×
21÷7=3 ( )
√
×
3x + 4 = 21 ○( )
3x - 8 = 21 ○( )
2、填空
已知 3x=21
3x × a = 21 ○( )
3x ○( )=21 ÷ b (b≠0)
+
4
—
8
×
a
÷
b
等式的性质2:
等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
等式的性质1:
等式两边都加上,或减去同一个数,左右两边仍然相等。
100g
100g
100g
50g
100+x=250
平衡
空杯子重100g,
水重x克。
X=?
100+x
100g
100g
100g
50g
平衡
100+x=250
X=?
100+150=250,
所以x=150。
100+x=100+150
假如两边同时减去100,就能得出x=150。
100+x=250
x=150
求方程的解的过程叫做解方程。
使方程左右两边相等的未知数的值,叫做
方程的解。
像上面,x=150就是方程100+x=250的解。
“方程的解”是指未知数的值,它是
一个数
“解方程”是求未知数X的值的
计算过程
我是这样理解解方程和方程的解的:
自主探究,构建新知
看图列方程,并求出方程的解。
①3x+4=40
②40-3x=4
③3x=40-4
汇报交流,发现总结
① 3x+4=40
解:3x+4-4=40-4
3x=36
x=12
3x÷3=36÷3
汇报交流,发现总结
② 40-3x=4
解:40-3x+3x=4+3x
40=4+3x
4+3x=40
3x=36
4+3x-4=40-4
x=12
3x÷3=36÷3
汇报交流,发现总结
3x+4=40
方程左边=3x+4
=3×12+4
=36+4
=方程右边
所以,x =12是方程的解。
=40
方法迁移,学会应用
解方程 2(x-16)=8
请你自己把这个方程解完。
方法迁移,学会应用
2(x-16)=8
方程左边=2(x-16)
=2×(20-16)
=2×4
=方程右边
所以,x=20是方程的解。
别忘了检验!
=8
看图列方程并求解。
x+3x=80
解: 4x=80
4x÷4=80÷4
x=20
方法迁移,学会应用
1.在解较复杂的方程时,可以把一个式子看作一个整体来解,然后利用等式的性质将复杂的方程转化成简单的方程。
2.在解方程时,也可以运用运算定律来解。
总结方法
1. 解方程。
6x-35=13
3x-42×6=6
巩固练习,提升认识
问题:1. 观察这个方程有几步运算?可以先把什么看做一个整体?
2. 请你独立思考并在纸上完成。
问题:1. 你能说说他们的想法吗?分别把什么看做一个整体?分几
大步解决?依据是什么?
巩固练习,提升认识
6x=48
解: 6x-35+35=13+35
6x-35=13
6x÷6=48÷6
x=8
3x-252+252=6+252
解: 3x-252=6
3x-42×6=6
3x=258
3x÷3=258÷3
x=86
2. 请你检验一下。
1. 解方程。
小结:在解两步、三步方程时,你有什么感悟?和大家分享一下。
巩固练习,提升认识
2. 看图列方程并求解。
问题:1. 你能根据图意列出方程吗?
2. 这个方程有几步运算?怎样解?把过程写下来。
3. 请你检验一下x=49是不是方程的解。
2x+30×2=158
方程左边=2x+30×2
=2×49+30×2
=98+60
=158
=方程右边
所以,x=49是方程的解。
解: 2x+60=158
2x+60-60=158-60
2x=98
2x÷2=98÷2
x=49
方程4.6+X=7.5和a-X=8.3中的X的值相同,求a的值是多少?
拓展训练:
4.6 +X= 7.5
解:4.6+X-4.6= 7.5-4.6
X = 2.9
a - 2.9 = 8.3
解:a - 2.9 +2.9= 8.3+2.9
a= 11.2
通过这节课的学习,
你有哪些收获
