青岛版2023-2024学年度上学期八年级期末检测数学试题一(含答案)
文档属性
| 名称 | 青岛版2023-2024学年度上学期八年级期末检测数学试题一(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-17 16:28:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
青岛版数学八年级上册期末考试模拟题
(时间:120分钟 分值:100分)
一、选择题(共12小题,每小题3分)
1.(4分)一台机床在十天内生产的产品中,每天出现的次品个数依次为(单位:个)0,2,0,2,3,0,2,3,1,2.那么,这十天中次品个数的( )
A.平均数是2 B.众数是3
C.中位数是1.5 D.方差是1.25
2.(4分)某工厂为了选择1名车工参加加工直径为10MM的精密零件的技术比赛,随机抽取甲、乙两名车工加工的5个零件,现测得的结果如下表,请你比较s甲2、S乙2的大小( )
甲 10.05 10.02 9.97 9.96 10
乙 10 10.01 10.02 9.97 10
A.S甲2>S乙2 B.S甲2=S乙2 C.S甲2<S乙2 D.S甲2≤S乙2
3.(4分)已知一组数据:5,15,75,45,25,75,45,35,45,35,那么40是这一组数据的( )
A.平均数但不是中位数 B.平均数也是中位数
C.众数 D.中位数但不是平均数
4.下列命题正确的是( )
A.三角形的中位线平行且等于第三边
B.对角线相等的四边形是等腰梯形
C.四条边都相等的四边形是菱形
D.相等的角是对顶角
5.下列命题中的真命题是( )
A.三个角相等的四边形是矩形
B.对角线互相垂直且相等的四边形是正方形
C.顺次连接矩形四边中点得到的四边形是菱形
D.正五边形既是轴对称图形又是中心对称图形
6.下列命题正确的个数是( )
①若代数式有意义,则x的取值范围为x≤1且x≠0.
②我市生态旅游初步形成规模,2012年全年生态旅游收入为302 600 000元,保留三个有效数字用科学记数法表示为3.03×108元.
③若反比例函数(m为常数),当x>0时,y随x增大而增大,则一次函数y=﹣2x+m的图象一定不经过第一象限.
④若函数的图象关于y轴对称,则函数称为偶函数,下列三个函数:y=3,y=2x+1,y=x2中偶函数的个数为2个.
A.1 B.2 C.3 D.4
7.(3分)若将分式中的x,y的值变为原来的100倍,则此分式的值( )
A.不变 B.是原来的100倍
C.是原来的200倍 D.是原来的
8.(3分)当a=﹣1时,分式( )
A.等于0 B.等于1 C.等于﹣1 D.无意义
9.(3分)化简的结果是( )
A. B. C. D.
10.(3分)某化肥厂原计划每天生产化肥x吨,由于采用了新技术,每天比计划多生产3吨,实际生产180吨化肥所用时间与原计划生产120吨化肥所用时间相同,那么适合题意的方程是( )
A.= B.=
C.= D.=
11.(3分)如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为( )
A.85° B.70° C.75° D.60°
12.(3分)已知:如图△ABC中,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )
A.①②③ B.①③④ C.①②④ D.①②③④
二、填空题(本题共5个小题,每小题3分,共15分)
13.(3分)分式,的最简公分母是 .
14.(3分)某校规定学生的体育成绩由三部分组成;体育技能测试占50%,体育理论测试占20%,体育课外活动表现30%,甲同学的上述三部分成绩依次为96分,85分,90分,则甲同学的体育成绩为 分.
15.(3分)若==,则的值为 .
16.(3分)若分式方程有增根,则m= .
17.(3分)如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E离开点A后,运动 秒时,△DEB与△BCA全等.
三、解答题(本大题共8小题,共69分)
18.(12分)计算
(1)
(2)
(3)﹣
(4)x﹣y+.
19.(10分)解分式方程:
(1)=1﹣.
(2)﹣=.
20.(5分)先化简,再求值:(﹣)÷,其中x=3.
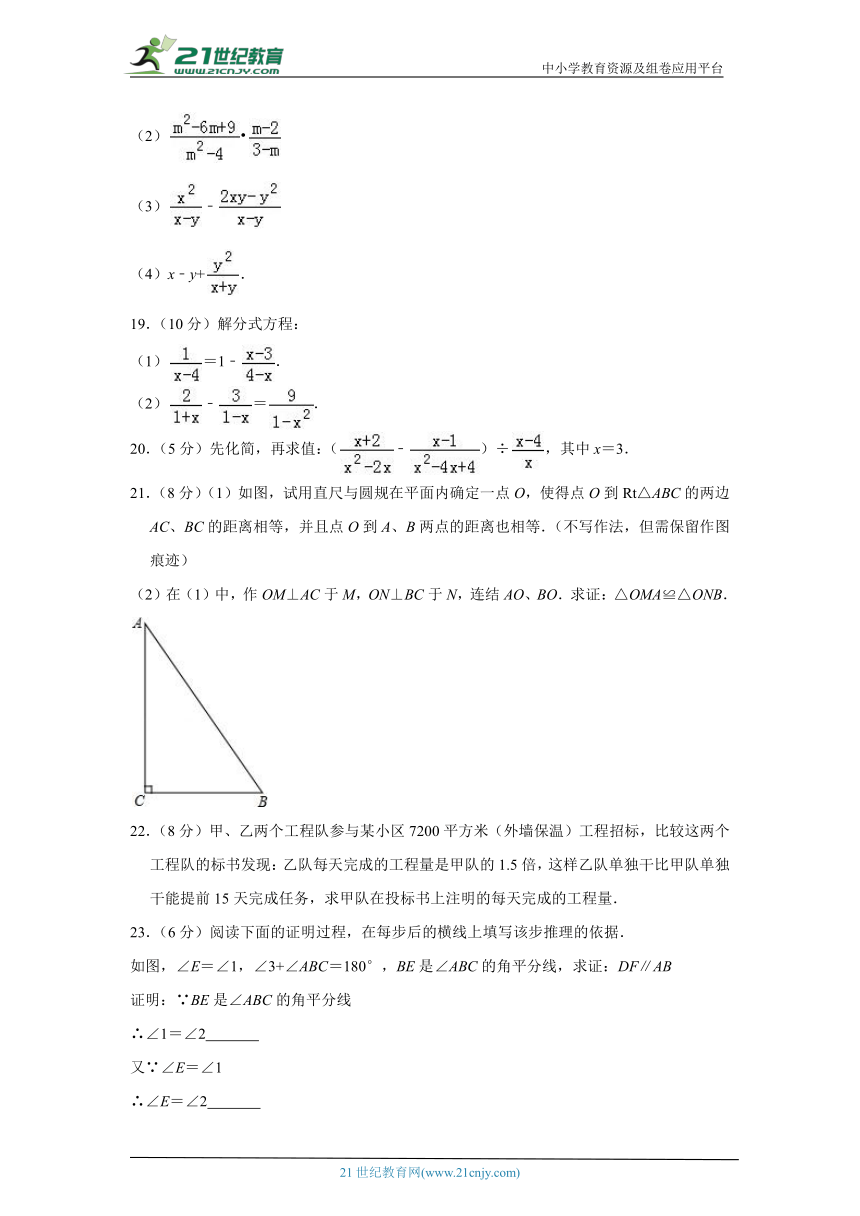
21.(8分)(1)如图,试用直尺与圆规在平面内确定一点O,使得点O到Rt△ABC的两边AC、BC的距离相等,并且点O到A、B两点的距离也相等.(不写作法,但需保留作图痕迹)
(2)在(1)中,作OM⊥AC于M,ON⊥BC于N,连结AO、BO.求证:△OMA≌△ONB.
22.(8分)甲、乙两个工程队参与某小区7200平方米(外墙保温)工程招标,比较这两个工程队的标书发现:乙队每天完成的工程量是甲队的1.5倍,这样乙队单独干比甲队单独干能提前15天完成任务,求甲队在投标书上注明的每天完成的工程量.
23.(6分)阅读下面的证明过程,在每步后的横线上填写该步推理的依据.
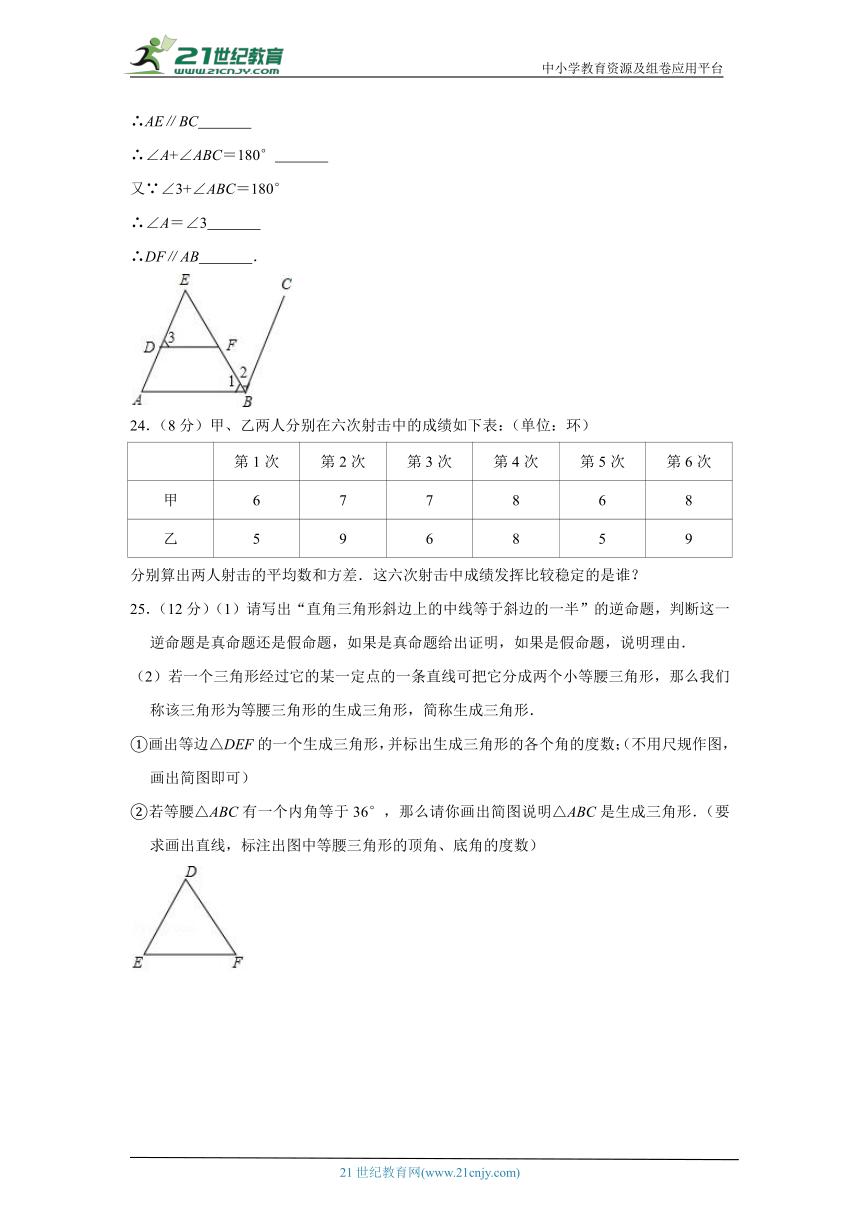
如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线,求证:DF∥AB
证明:∵BE是∠ABC的角平分线
∴∠1=∠2
又∵∠E=∠1
∴∠E=∠2
∴AE∥BC
∴∠A+∠ABC=180°
又∵∠3+∠ABC=180°
∴∠A=∠3
∴DF∥AB .
24.(8分)甲、乙两人分别在六次射击中的成绩如下表:(单位:环)
第1次 第2次 第3次 第4次 第5次 第6次
甲 6 7 7 8 6 8
乙 5 9 6 8 5 9
分别算出两人射击的平均数和方差.这六次射击中成绩发挥比较稳定的是谁?
25.(12分)(1)请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题,判断这一逆命题是真命题还是假命题,如果是真命题给出证明,如果是假命题,说明理由.
(2)若一个三角形经过它的某一定点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形的生成三角形,简称生成三角形.
①画出等边△DEF的一个生成三角形,并标出生成三角形的各个角的度数;(不用尺规作图,画出简图即可)
②若等腰△ABC有一个内角等于36°,那么请你画出简图说明△ABC是生成三角形.(要求画出直线,标注出图中等腰三角形的顶角、底角的度数)
参考答案
一、选择题。
1.D.
2.A.
3.B.
4.C.
5.C.
6.C.
7.B.
8.D.
9.D.
10.A.
11.C.
12.D.
二、填空题。
13. 6x3(x﹣y).
14.92.
15﹣.
16.2.
17.2,6,8.
三、解答题。
18.解:(1)
=.
(2)
=×
=﹣.
(3)﹣
=
=
=x﹣y.
(4)x﹣y+
=+
=
=.
19.解:(1)去分母得:1=x﹣4+x﹣3,
解得:x=4,
经检验x=4是增根,原分式方程无根;
(2)去分母得:2﹣2x﹣3﹣3x=9,
解得:x=﹣2,
经检验x=﹣2是分式方程的解.
20.解:原式=[﹣]÷,
=×,
=×,
=,
当x=3时,原式==1.
21.解:(1)如图1,
(2)如图2,
∵OC平分∠ACB,OM⊥AC,ON⊥CN,
∴OM=ON,
∵点O在线段AB的垂直平分线上,
∴OA=OB,
在Rt△△OMA和△ONB中,
,
∴△OMA≌△ONB.
22.解:设甲队每天完成x米2,乙队每天完成1.5 x米2,根据题意得.
=15,
解得x=160,
经检验,x=160,是所列方程的解.
答:甲队每天完成160米2.
23.解:证明:∵BE是∠ABC的角平分线
∴∠1=∠2(角的平分线的定义),
又∵∠E=∠1
∴∠E=∠2 (等量代换)
∴AE∥BC (内错角相等,两直线平行),
∴∠A+∠ABC=180° (两直线平行,同旁内角互补),
又∵∠3+∠ABC=180°
∴∠A=∠3 (同角的补角相等),
∴DF∥AB(同位角相等,两直线平行).
故答案是:角的平分线的定义;等量代换;内错角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等;同位角相等,两直线平行.
24.解:∵甲=(6+7+7+8+6+8)=7,乙=(5+9+6+8+5+9)=7;
∴S2甲=[(6﹣7)2+(7﹣7)2+(7﹣7)2+(8﹣7)2+(6﹣7)2+(8﹣7)2]=,
S2乙=[(5﹣7)2+(9﹣7)2+(6﹣7)2+(8﹣7)2+(5﹣7)2+(9﹣7)2]=3;
∴S2甲<S2乙,
∴甲在射击中成绩发挥比较稳定.
25.解:(1)逆命题是:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
已知,如图,△ABC中,D是AB边的中点,且CD=AB.
求证:△ABC是直角三角形.
证明:∵D是AB边的中点,且CD=AB,
∴AD=BD=CD,
∵AD=CD,
∴∠ACD=∠A,
∵BD=CD,
∴∠BCD=∠B,
又∵∠ACD+∠BCD+∠A+∠B=180°,
∴2(∠ACD+∠BCD)=180°,
∴∠ACD+∠BCD=90°,
∴∠ACB=90°,
∴△ABC是直角三角形.
(2)①如图所示,△DEG即为所求,其中∠E=60°,∠G=30°,∠EDG=90°;
②如图所示,等腰△ABC是生成三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
青岛版数学八年级上册期末考试模拟题
(时间:120分钟 分值:100分)
一、选择题(共12小题,每小题3分)
1.(4分)一台机床在十天内生产的产品中,每天出现的次品个数依次为(单位:个)0,2,0,2,3,0,2,3,1,2.那么,这十天中次品个数的( )
A.平均数是2 B.众数是3
C.中位数是1.5 D.方差是1.25
2.(4分)某工厂为了选择1名车工参加加工直径为10MM的精密零件的技术比赛,随机抽取甲、乙两名车工加工的5个零件,现测得的结果如下表,请你比较s甲2、S乙2的大小( )
甲 10.05 10.02 9.97 9.96 10
乙 10 10.01 10.02 9.97 10
A.S甲2>S乙2 B.S甲2=S乙2 C.S甲2<S乙2 D.S甲2≤S乙2
3.(4分)已知一组数据:5,15,75,45,25,75,45,35,45,35,那么40是这一组数据的( )
A.平均数但不是中位数 B.平均数也是中位数
C.众数 D.中位数但不是平均数
4.下列命题正确的是( )
A.三角形的中位线平行且等于第三边
B.对角线相等的四边形是等腰梯形
C.四条边都相等的四边形是菱形
D.相等的角是对顶角
5.下列命题中的真命题是( )
A.三个角相等的四边形是矩形
B.对角线互相垂直且相等的四边形是正方形
C.顺次连接矩形四边中点得到的四边形是菱形
D.正五边形既是轴对称图形又是中心对称图形
6.下列命题正确的个数是( )
①若代数式有意义,则x的取值范围为x≤1且x≠0.
②我市生态旅游初步形成规模,2012年全年生态旅游收入为302 600 000元,保留三个有效数字用科学记数法表示为3.03×108元.
③若反比例函数(m为常数),当x>0时,y随x增大而增大,则一次函数y=﹣2x+m的图象一定不经过第一象限.
④若函数的图象关于y轴对称,则函数称为偶函数,下列三个函数:y=3,y=2x+1,y=x2中偶函数的个数为2个.
A.1 B.2 C.3 D.4
7.(3分)若将分式中的x,y的值变为原来的100倍,则此分式的值( )
A.不变 B.是原来的100倍
C.是原来的200倍 D.是原来的
8.(3分)当a=﹣1时,分式( )
A.等于0 B.等于1 C.等于﹣1 D.无意义
9.(3分)化简的结果是( )
A. B. C. D.
10.(3分)某化肥厂原计划每天生产化肥x吨,由于采用了新技术,每天比计划多生产3吨,实际生产180吨化肥所用时间与原计划生产120吨化肥所用时间相同,那么适合题意的方程是( )
A.= B.=
C.= D.=
11.(3分)如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为( )
A.85° B.70° C.75° D.60°
12.(3分)已知:如图△ABC中,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )
A.①②③ B.①③④ C.①②④ D.①②③④
二、填空题(本题共5个小题,每小题3分,共15分)
13.(3分)分式,的最简公分母是 .
14.(3分)某校规定学生的体育成绩由三部分组成;体育技能测试占50%,体育理论测试占20%,体育课外活动表现30%,甲同学的上述三部分成绩依次为96分,85分,90分,则甲同学的体育成绩为 分.
15.(3分)若==,则的值为 .
16.(3分)若分式方程有增根,则m= .
17.(3分)如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E离开点A后,运动 秒时,△DEB与△BCA全等.
三、解答题(本大题共8小题,共69分)
18.(12分)计算
(1)
(2)
(3)﹣
(4)x﹣y+.
19.(10分)解分式方程:
(1)=1﹣.
(2)﹣=.
20.(5分)先化简,再求值:(﹣)÷,其中x=3.
21.(8分)(1)如图,试用直尺与圆规在平面内确定一点O,使得点O到Rt△ABC的两边AC、BC的距离相等,并且点O到A、B两点的距离也相等.(不写作法,但需保留作图痕迹)
(2)在(1)中,作OM⊥AC于M,ON⊥BC于N,连结AO、BO.求证:△OMA≌△ONB.
22.(8分)甲、乙两个工程队参与某小区7200平方米(外墙保温)工程招标,比较这两个工程队的标书发现:乙队每天完成的工程量是甲队的1.5倍,这样乙队单独干比甲队单独干能提前15天完成任务,求甲队在投标书上注明的每天完成的工程量.
23.(6分)阅读下面的证明过程,在每步后的横线上填写该步推理的依据.
如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线,求证:DF∥AB
证明:∵BE是∠ABC的角平分线
∴∠1=∠2
又∵∠E=∠1
∴∠E=∠2
∴AE∥BC
∴∠A+∠ABC=180°
又∵∠3+∠ABC=180°
∴∠A=∠3
∴DF∥AB .
24.(8分)甲、乙两人分别在六次射击中的成绩如下表:(单位:环)
第1次 第2次 第3次 第4次 第5次 第6次
甲 6 7 7 8 6 8
乙 5 9 6 8 5 9
分别算出两人射击的平均数和方差.这六次射击中成绩发挥比较稳定的是谁?
25.(12分)(1)请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题,判断这一逆命题是真命题还是假命题,如果是真命题给出证明,如果是假命题,说明理由.
(2)若一个三角形经过它的某一定点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形的生成三角形,简称生成三角形.
①画出等边△DEF的一个生成三角形,并标出生成三角形的各个角的度数;(不用尺规作图,画出简图即可)
②若等腰△ABC有一个内角等于36°,那么请你画出简图说明△ABC是生成三角形.(要求画出直线,标注出图中等腰三角形的顶角、底角的度数)
参考答案
一、选择题。
1.D.
2.A.
3.B.
4.C.
5.C.
6.C.
7.B.
8.D.
9.D.
10.A.
11.C.
12.D.
二、填空题。
13. 6x3(x﹣y).
14.92.
15﹣.
16.2.
17.2,6,8.
三、解答题。
18.解:(1)
=.
(2)
=×
=﹣.
(3)﹣
=
=
=x﹣y.
(4)x﹣y+
=+
=
=.
19.解:(1)去分母得:1=x﹣4+x﹣3,
解得:x=4,
经检验x=4是增根,原分式方程无根;
(2)去分母得:2﹣2x﹣3﹣3x=9,
解得:x=﹣2,
经检验x=﹣2是分式方程的解.
20.解:原式=[﹣]÷,
=×,
=×,
=,
当x=3时,原式==1.
21.解:(1)如图1,
(2)如图2,
∵OC平分∠ACB,OM⊥AC,ON⊥CN,
∴OM=ON,
∵点O在线段AB的垂直平分线上,
∴OA=OB,
在Rt△△OMA和△ONB中,
,
∴△OMA≌△ONB.
22.解:设甲队每天完成x米2,乙队每天完成1.5 x米2,根据题意得.
=15,
解得x=160,
经检验,x=160,是所列方程的解.
答:甲队每天完成160米2.
23.解:证明:∵BE是∠ABC的角平分线
∴∠1=∠2(角的平分线的定义),
又∵∠E=∠1
∴∠E=∠2 (等量代换)
∴AE∥BC (内错角相等,两直线平行),
∴∠A+∠ABC=180° (两直线平行,同旁内角互补),
又∵∠3+∠ABC=180°
∴∠A=∠3 (同角的补角相等),
∴DF∥AB(同位角相等,两直线平行).
故答案是:角的平分线的定义;等量代换;内错角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等;同位角相等,两直线平行.
24.解:∵甲=(6+7+7+8+6+8)=7,乙=(5+9+6+8+5+9)=7;
∴S2甲=[(6﹣7)2+(7﹣7)2+(7﹣7)2+(8﹣7)2+(6﹣7)2+(8﹣7)2]=,
S2乙=[(5﹣7)2+(9﹣7)2+(6﹣7)2+(8﹣7)2+(5﹣7)2+(9﹣7)2]=3;
∴S2甲<S2乙,
∴甲在射击中成绩发挥比较稳定.
25.解:(1)逆命题是:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
已知,如图,△ABC中,D是AB边的中点,且CD=AB.
求证:△ABC是直角三角形.
证明:∵D是AB边的中点,且CD=AB,
∴AD=BD=CD,
∵AD=CD,
∴∠ACD=∠A,
∵BD=CD,
∴∠BCD=∠B,
又∵∠ACD+∠BCD+∠A+∠B=180°,
∴2(∠ACD+∠BCD)=180°,
∴∠ACD+∠BCD=90°,
∴∠ACB=90°,
∴△ABC是直角三角形.
(2)①如图所示,△DEG即为所求,其中∠E=60°,∠G=30°,∠EDG=90°;
②如图所示,等腰△ABC是生成三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
