6.4.3.3余弦定理、正弦定理应用举例 课件(共16张PPT)
文档属性
| 名称 | 6.4.3.3余弦定理、正弦定理应用举例 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-17 20:07:20 | ||
图片预览

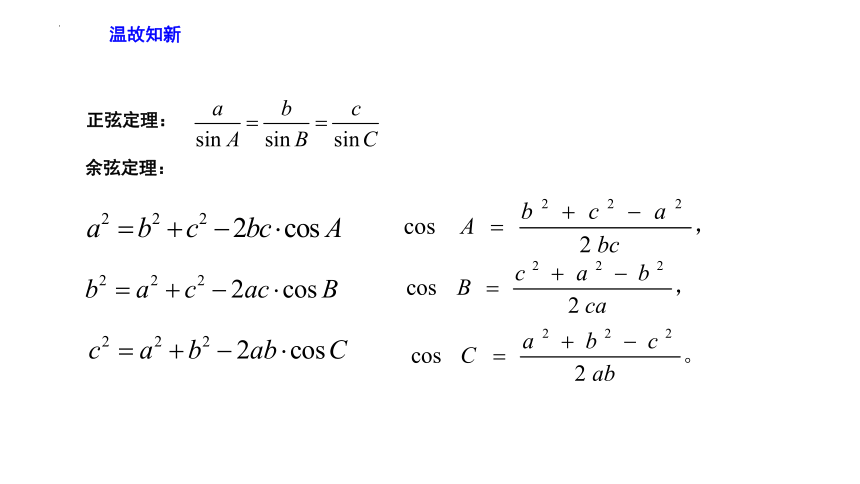


文档简介
(共16张PPT)
6.4.3 余弦定理、正弦定理应用举例
温故知新
正弦定理:
余弦定理:
探究新知
在我国古代就有嫦娥奔月的神话故事,我们仰望星空,明月高悬,不禁会问,遥不可及的月亮离地球究竟有多远呢?
早在1671年,两个法国天文学家就测出了地球与月球之间的距离大约为385400km。他们是怎样测出两者之间距离的呢?
下面让我们一起探讨解决不可到达的距离的测量问题。
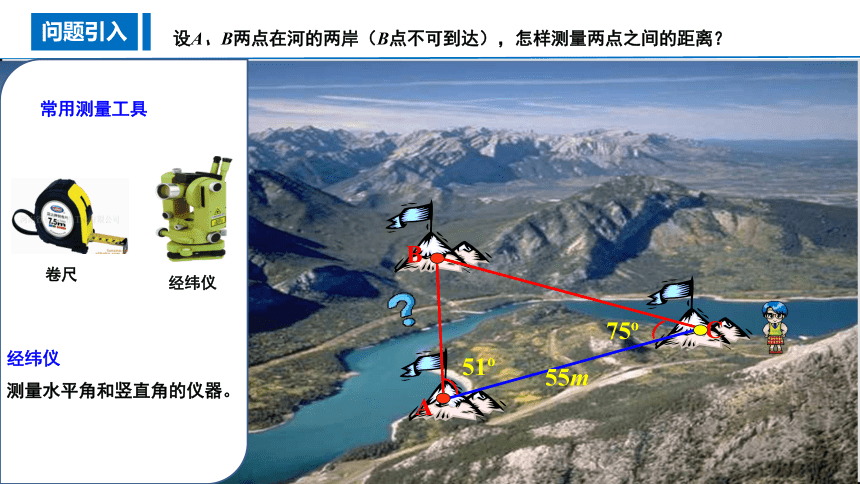
问题引入
A
C
B
51o
55m
75o
设A、B两点在河的两岸(B点不可到达),怎样测量两点之间的距离?
常用测量工具
卷尺
经纬仪
经纬仪
测量水平角和竖直角的仪器。
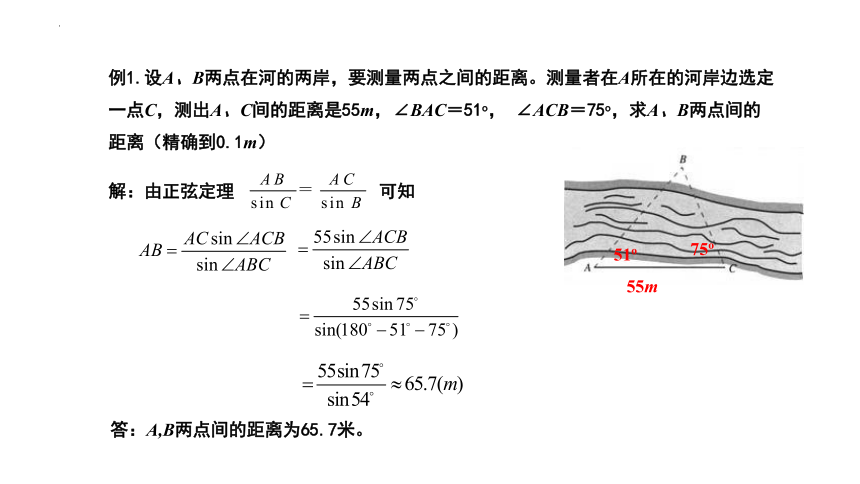
例1.设A、B两点在河的两岸,要测量两点之间的距离。测量者在A所在的河岸边选定一点C,测出A、C间的距离是55m,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m)
解:由正弦定理 可知
答:A,B两点间的距离为65.7米。
51o
55m
75o
水平距离的测量——两点能相互看到,但不能到达
(1)选基点C,测量AC的长;
(2)测量角A和角C的大小;
(3)由三角形的内角和,求出角B;
基线的概念
在测量过程中,我们把根据测量的需要而确定的线段叫做基线.
基线的选取不唯一,一般来说基线越长,测量的精确度越高.
(4)由正弦定理,可求边AB的长.
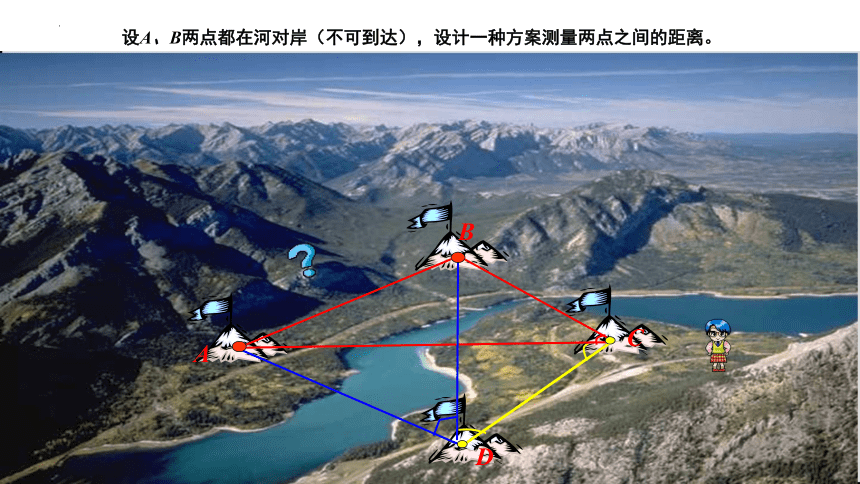
设A、B两点都在河对岸(不可到达),设计一种方案测量两点之间的距离。
A
B
C
D
A
B
C
D
α
β
γ
δ
a
解:如图,测量者可以在河岸边选定两点C、D,
设∠BCA=α,∠ACD=β,∠CDB=γ,∠ADB=δ,CD=a
,应用正弦定理得
在△ABC中,由余弦定理得
(2)在△ACD中,求出角∠ADC,
由正弦定理
求出AC的长;
(3)在△BCD中,求出角∠DBC,
由正弦定理
求出BC的长;
(4)在△ABC中,由余弦定理
求得AB的长。
水平距离的测量——两点都不能到达
(1) 选基点C,D,测量基线CD的长,
测量图中所示的角;
A
B
C
D
α
β
γ
δ
a
如图,在铁路建设中,需要确定隧道两端A,B的距离,请你设计一种测量A,B距离的方案?
转化为例2的思路进行测量,从而解决问题
学以致用
(3)由余弦定理得
(1)选取基点C,测量得出AC、BC的距离为b、a;
(2)测量角C为α;
想一想
测量高度问题
例3:如图,AB是底部B不可到达的一座建筑物,A为建筑物的最高点.设计一种测量建筑物AB的方法,并求出建筑物的高度.
测量术语——仰角
在测量时,视线与水平线所成的角中,
视线在水平线上方的角叫仰角(如图)
B
E
A
G
H
D
C
测量高度问题
解:选择一条水平基线HG,使H,G,B三点在同一条直线上。
在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,
测角仪器的高是h.
例3:如图,AB是底部B不可到达的一座建筑物,A为建筑物的最高点.设计一种测量建筑物AB的方法,并求出建筑物的高度.
在三角形ACD中,根据正弦定理可得
测量垂直高度AB
1、底部可以到达的
测量出角C和BC的长度,解直角三角形即可求出AB的长。
2、底部不能到达的
找基点C、D且与B共线,测量基线CD,测量∠C和∠ADB,
C
D
A
B
注意:在实际操作时,使C,D,B三点共线不是一件容易的事情。你有什么解决方法?
例4:位于某海域A处的甲船获悉,在其正东方向相距20海里的B处有一艘渔船遇险后抛锚等待营救.甲船立即前往救援,同时把消息告知位于甲船的南偏西30 ,且与甲船相距7海里C处的乙船.那么乙船前往营救遇险渔船时的目标方向线(由观测点看目标的视线)的方向是北偏东多少度(精确到1 )?需航行的距离是多少海里(精确到1海里)?
测量角度问题
A
B
北
20海里
7海里
C
30
解:根据题意画出示意图,由余弦定理可得
所以
由正弦定理可得
,于是
由于
,所以
答:乙船前往营救遇险渔船航行的方向约是北偏东
,大约航行24海里
课堂小结
1、本节课通过具体实例,研究了利用正弦定理及余弦定理解决实际测量问题。
实际问题
数学模型
实际问题的解
数学模型的解
画图形
解三角形
检验(答)
2.解三角形在实际测量中的常见问题
(1)距离问题
(2)高度问题
(3)角度问题
常用测量术语
1、仰角、俯角:
在测量时,视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角。(如图)
2、方向角:
指北或指南方向线与目标方向线所成的小于90°的水平角,如图
3、方位角:
从正北方向顺时针转到目标方向的夹角。
6.4.3 余弦定理、正弦定理应用举例
温故知新
正弦定理:
余弦定理:
探究新知
在我国古代就有嫦娥奔月的神话故事,我们仰望星空,明月高悬,不禁会问,遥不可及的月亮离地球究竟有多远呢?
早在1671年,两个法国天文学家就测出了地球与月球之间的距离大约为385400km。他们是怎样测出两者之间距离的呢?
下面让我们一起探讨解决不可到达的距离的测量问题。
问题引入
A
C
B
51o
55m
75o
设A、B两点在河的两岸(B点不可到达),怎样测量两点之间的距离?
常用测量工具
卷尺
经纬仪
经纬仪
测量水平角和竖直角的仪器。
例1.设A、B两点在河的两岸,要测量两点之间的距离。测量者在A所在的河岸边选定一点C,测出A、C间的距离是55m,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m)
解:由正弦定理 可知
答:A,B两点间的距离为65.7米。
51o
55m
75o
水平距离的测量——两点能相互看到,但不能到达
(1)选基点C,测量AC的长;
(2)测量角A和角C的大小;
(3)由三角形的内角和,求出角B;
基线的概念
在测量过程中,我们把根据测量的需要而确定的线段叫做基线.
基线的选取不唯一,一般来说基线越长,测量的精确度越高.
(4)由正弦定理,可求边AB的长.
设A、B两点都在河对岸(不可到达),设计一种方案测量两点之间的距离。
A
B
C
D
A
B
C
D
α
β
γ
δ
a
解:如图,测量者可以在河岸边选定两点C、D,
设∠BCA=α,∠ACD=β,∠CDB=γ,∠ADB=δ,CD=a
,应用正弦定理得
在△ABC中,由余弦定理得
(2)在△ACD中,求出角∠ADC,
由正弦定理
求出AC的长;
(3)在△BCD中,求出角∠DBC,
由正弦定理
求出BC的长;
(4)在△ABC中,由余弦定理
求得AB的长。
水平距离的测量——两点都不能到达
(1) 选基点C,D,测量基线CD的长,
测量图中所示的角;
A
B
C
D
α
β
γ
δ
a
如图,在铁路建设中,需要确定隧道两端A,B的距离,请你设计一种测量A,B距离的方案?
转化为例2的思路进行测量,从而解决问题
学以致用
(3)由余弦定理得
(1)选取基点C,测量得出AC、BC的距离为b、a;
(2)测量角C为α;
想一想
测量高度问题
例3:如图,AB是底部B不可到达的一座建筑物,A为建筑物的最高点.设计一种测量建筑物AB的方法,并求出建筑物的高度.
测量术语——仰角
在测量时,视线与水平线所成的角中,
视线在水平线上方的角叫仰角(如图)
B
E
A
G
H
D
C
测量高度问题
解:选择一条水平基线HG,使H,G,B三点在同一条直线上。
在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,
测角仪器的高是h.
例3:如图,AB是底部B不可到达的一座建筑物,A为建筑物的最高点.设计一种测量建筑物AB的方法,并求出建筑物的高度.
在三角形ACD中,根据正弦定理可得
测量垂直高度AB
1、底部可以到达的
测量出角C和BC的长度,解直角三角形即可求出AB的长。
2、底部不能到达的
找基点C、D且与B共线,测量基线CD,测量∠C和∠ADB,
C
D
A
B
注意:在实际操作时,使C,D,B三点共线不是一件容易的事情。你有什么解决方法?
例4:位于某海域A处的甲船获悉,在其正东方向相距20海里的B处有一艘渔船遇险后抛锚等待营救.甲船立即前往救援,同时把消息告知位于甲船的南偏西30 ,且与甲船相距7海里C处的乙船.那么乙船前往营救遇险渔船时的目标方向线(由观测点看目标的视线)的方向是北偏东多少度(精确到1 )?需航行的距离是多少海里(精确到1海里)?
测量角度问题
A
B
北
20海里
7海里
C
30
解:根据题意画出示意图,由余弦定理可得
所以
由正弦定理可得
,于是
由于
,所以
答:乙船前往营救遇险渔船航行的方向约是北偏东
,大约航行24海里
课堂小结
1、本节课通过具体实例,研究了利用正弦定理及余弦定理解决实际测量问题。
实际问题
数学模型
实际问题的解
数学模型的解
画图形
解三角形
检验(答)
2.解三角形在实际测量中的常见问题
(1)距离问题
(2)高度问题
(3)角度问题
常用测量术语
1、仰角、俯角:
在测量时,视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角。(如图)
2、方向角:
指北或指南方向线与目标方向线所成的小于90°的水平角,如图
3、方位角:
从正北方向顺时针转到目标方向的夹角。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
