第二十五章 图形的相似单元练习(含解析)
文档属性
| 名称 | 第二十五章 图形的相似单元练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-17 17:02:50 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第二十五章 图形的相似 单元练习 2023-2024学年 冀教版(2012)九年级数学上册(含解析)
一、单选题
1.(2022秋·辽宁丹东·九年级统考期末)如图,点是线段的黄金分割点,且,下列选项错误的是( )
A. B.
C. D.
2.(2022秋·安徽六安·九年级校考期末)如图,,两条直线与这三条平行线分别交于点A、、和、、,若,则的值为( )
A. B. C. D.
3.(2022秋·浙江舟山·九年级统考期末)如图,在△ABC中,EF//BC,EG//AB,则下列式子一定正确的是( )
A. B.
C. D.
4.(2022秋·山西临汾·九年级统考期末)如图,每个小正方形边长均为1,则图中的三角形中与相似的是( )
A. B. C. D.
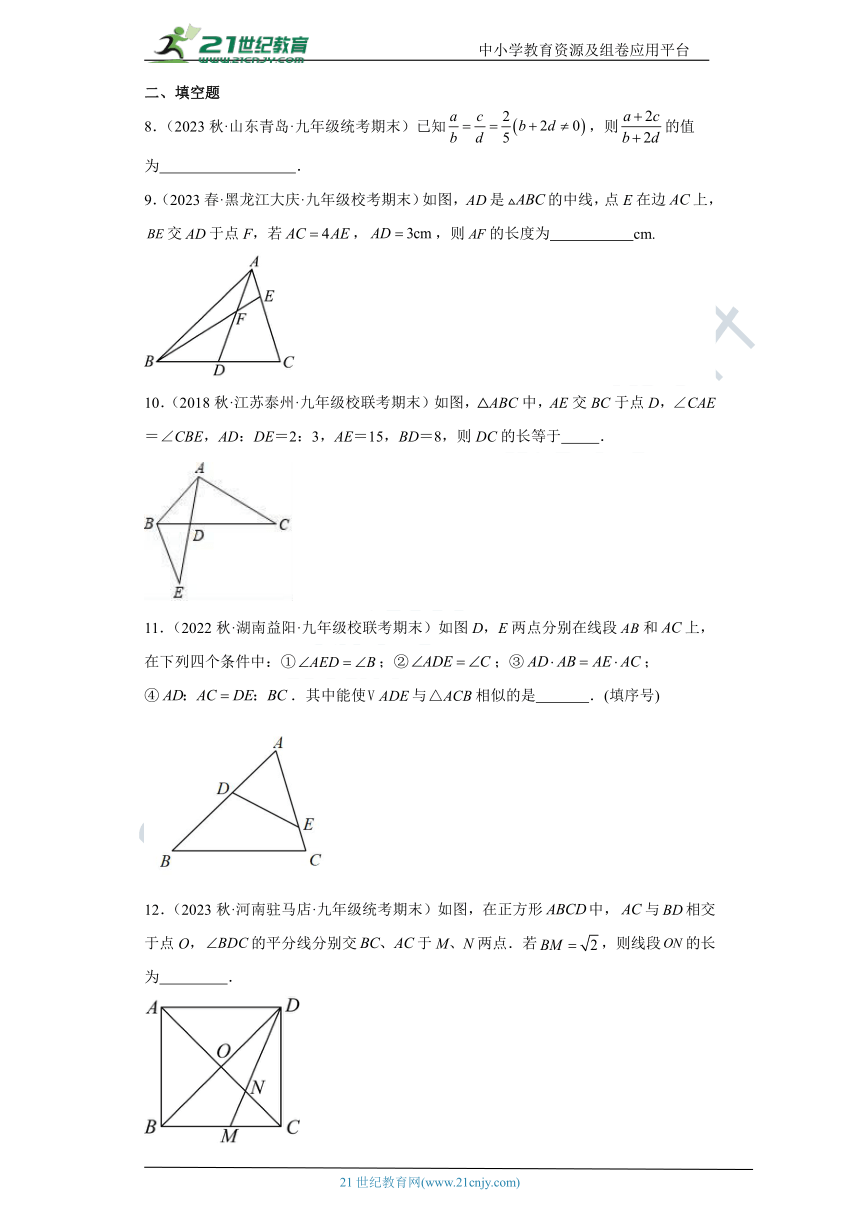
5.(2023秋·海南海口·九年级统考期末)如图,在中,是的中点,,若的面积为4,则四边形的面积为( )
A.8 B.10 C.12 D.16
6.(2023秋·江西萍乡·九年级统考期末)如图,圆桌上方的灯泡(看作一个点)发出的光线照射桌面后,在地面形成阴影,已知桌面的直径为,桌面距离地面,若灯泡距离地面,则地面上阴影部分面积为( )
A. B. C. D.
7.(2020秋·广东揭阳·九年级统考期末)如图,,,分别是,,的中点,下面的说法中:①与是位似图形;②与的相似比为;③与的周长之比为;④与的面积之比为.正确的是( )
A.①②③ B.①③④ C.①②④ D.②③④
二、填空题
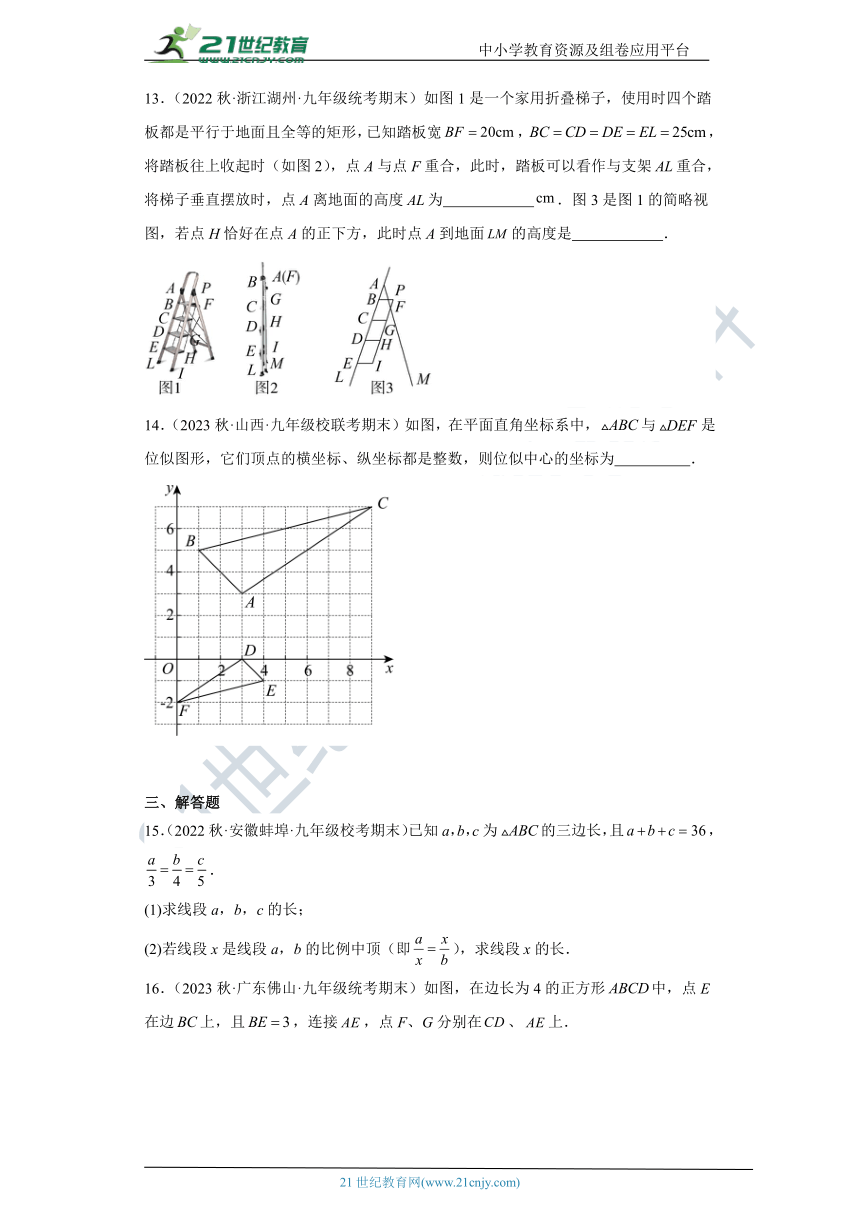
8.(2023秋·山东青岛·九年级统考期末)已知,则的值为 .
9.(2023春·黑龙江大庆·九年级校考期末)如图,是的中线,点E在边上,交于点F,若,,则的长度为 cm.
10.(2018秋·江苏泰州·九年级校联考期末)如图,△ABC中,AE交BC于点D,∠CAE=∠CBE,AD:DE=2:3,AE=15,BD=8,则DC的长等于 .
11.(2022秋·湖南益阳·九年级校联考期末)如图D,E两点分别在线段和上,在下列四个条件中:①;②;③;④.其中能使与相似的是 .(填序号)
12.(2023秋·河南驻马店·九年级统考期末)如图,在正方形中,与相交于点O,的平分线分别交于M、N两点.若,则线段的长为 .
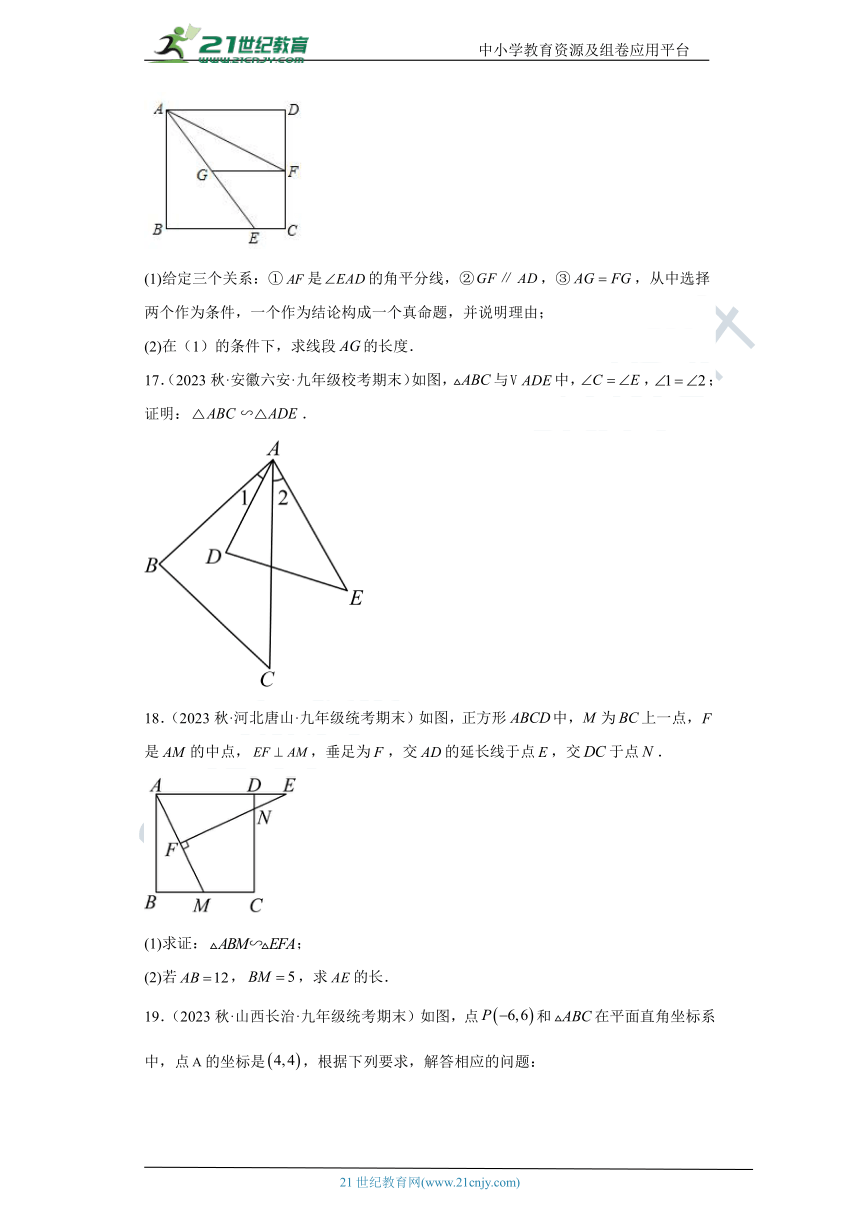
13.(2022秋·浙江湖州·九年级统考期末)如图1是一个家用折叠梯子,使用时四个踏板都是平行于地面且全等的矩形,已知踏板宽,,将踏板往上收起时(如图2),点A与点F重合,此时,踏板可以看作与支架重合,将梯子垂直摆放时,点A离地面的高度为 .图3是图1的简略视图,若点H恰好在点A的正下方,此时点A到地面的高度是 .
14.(2023秋·山西·九年级校联考期末)如图,在平面直角坐标系中,与是位似图形,它们顶点的横坐标、纵坐标都是整数,则位似中心的坐标为 .
三、解答题
15.(2022秋·安徽蚌埠·九年级校考期末)已知a,b,c为的三边长,且,.
(1)求线段a,b,c的长;
(2)若线段x是线段a,b的比例中顶(即),求线段x的长.
16.(2023秋·广东佛山·九年级统考期末)如图,在边长为4的正方形中,点E在边上,且,连接,点F、G分别在、上.
(1)给定三个关系:①是的角平分线,②,③,从中选择两个作为条件,一个作为结论构成一个真命题,并说明理由;
(2)在(1)的条件下,求线段的长度.
17.(2023秋·安徽六安·九年级校考期末)如图,与中,,;证明:.
18.(2023秋·河北唐山·九年级统考期末)如图,正方形中,为上一点,是的中点,,垂足为,交的延长线于点,交于点.
(1)求证:;
(2)若,,求的长.
19.(2023秋·山西长治·九年级统考期末)如图,点和在平面直角坐标系中,点的坐标是,根据下列要求,解答相应的问题:
(1)作关于轴对称的,直接写出点的对应点的坐标;
(2)作关于点成位似中心的位似,与的相似比为,且这两个三角形在点同侧,直接写出点的对应点的坐标.
20.(2022秋·广东梅州·九年级统考期末)北京时间年月日时分,神舟十五号载人飞船成功发射,为弘扬航天精神,某校在教学楼上悬挂了一幅励志条幅(即).小亮同学想知道条幅的长度,他的测量过程如下:如图,刚开始他站在距离教学楼的点处,在点正上方点处测得,然后向教学楼条幅方向前行到达点处,在点正上方点处测得,若,,均为,的长为.
(1)如图1,请你帮助小亮计算条幅长度
(2)若小亮从点开始以每秒的速度向点行走至(正上方点),经过多少秒后,以、、为顶点的三角形与相似.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】根据黄金分割的定义得,即可解决问题.
【详解】解:点是线段的黄金分割点,且,
,
,,
A、C、D选项不符合题意,
故选:B.
【点睛】本题考查了黄金分割,解题的关键是掌握黄金分割的定义:把一条线段分割为两部分,使较大部分与全长的比值等于较小部分与较大的比值,这个比值为,近似值为,即为黄金分割.
2.A
【分析】根据平行线分线段成比例定理得到,根据合比性质即得.
【详解】,
,
.
故选:A.
【点睛】本题主要考查了平行线分线段,解决问题的关键是熟练掌握平行线分线段成比例定理,合比性质.
3.D
【分析】根据平行线分线段成比例定理逐一判断即可.
【详解】∵EG//AB,EF//BC,
∴,
∵AC≠EC
∴不成立,
∴选项A错误;
∵EG//AB,EF//BC,
∴,,
∵AE≠EC,
∴不成立,
∴选项B错误;
∵EG//AB,EF//BC,
∴,
∵DF≠AF
∴不成立,
∴选项C错误;
∵EG//AB,EF//BC,
∴,,
∴,
∴选项D正确;
故选D.
【点睛】本题考查了平行线分线段成比例定理,熟练掌握定理,特别是比例中对应线段的属性保持一致是解题的关键.
4.B
【分析】直接利用相似三角形的判定方法结合正方形的性质分析得出答案.
【详解】解:由题意可得:,,
,,,,
,,
,
又,
.
故选:B.
【点睛】此题主要考查了相似三角形的判定,正确得出对应边的关系是解题关键.
5.C
【分析】根据相似三角形的性质得出的面积,即可求出答案.
【详解】解:∵点D是的中点,
∴
∵
∴,
∴,
∴
∴四边形的面积为,
故选:C.
【点睛】本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定.
6.D
【分析】欲求投影圆的面积,可先求出其直径,而直径可通过构造相似三角形,由相似三角形性质求出.
【详解】解:构造几何模型如图:
依题意知,,
∴,
∴,即,
∴,
∴ ,
故选:D.
【点睛】本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力.利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
7.B
【分析】根据位似图形的性质,得出①与是位似图形,进而根据位似图形一定是相似图形得出 ②与是相似图形,再根据周长比等于位似比,以及根据面积比等于相似比的平方,即可得出答案.
【详解】解:根据位似性质得出:
①与是位似图形,
②与是相似图形,且相似比是:,
③与的周长比等于相似比,即,
④根据面积比等于相似比的平方,则与的面积比为.
综上所述,正确的结论是:①③④.
故选:B.
【点睛】本题考查了位似的相关知识,位似是相似的特殊形式,位似比等于相似比,其对应的面积比等于相似比的平方.
8./
【分析】先求出,再根据比例的性质即可得.
【详解】解:,
,
,
故答案为:.
【点睛】本题考查了比例的性质,熟练掌握比例的性质是解题关键.
9.1.2
【分析】过D点作交于G点,如图,利用得到,则,所以,再利用得到,然后利用比例的性质求.
【详解】解:过D点作交于G点,如图,
∵是的中线,
∴,
∵,
∴,
∵,
∴,即,
∴,
∵,
∴,
∴,
∴.
故答案为1.2.
【点睛】本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.作为解题的关键.
10..
【分析】根据相似三角形的性质与判定即可求出答案.
【详解】解:由题意可知AD:DE=2:3,AE=15,
∴AD=6,DE=9,
∵∠CAE=∠CBE,∠BDE=∠ADE,
∴△BDE∽△ADC,
∴,
∴,
∴CD=,
故答案为.
【点睛】本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于中等题型.
11.①②③
【分析】根据相似三角形的判定定理逐个排查即可.
【详解】解:∵,
∴根据 “两个三角形的两个角分别对应相等,则三角形相似”可证,故①满足题意;
∵,
∴根据 “两个三角形的两个角分别对应相等,则三角形相似”可证,故②满足题意;
∵
∴
∴根据 “两边对应成比例且夹角相等,两个三角形相似”可证,故③满足题意;
∵,而与不一定相等,故④不满足题意,
∴综上可得:①②③符合题意.
故答案为①②③.
【点睛】本题主要考查了相似三角形的判定,灵活运用相似三角形的判定定理是解答本题的关键.
12.
【分析】过M点作,根据等腰直角三角形的性质求出长,再根据角平分线性质可得长,由此得到正方形的边长,求出和长,根据得到,得出,从而可求长.
【详解】解:过M点作,
∵四边形是正方形,是对角线,
∴,
∴,,
∴.
∵平分,
∴.
∴正方形边长,
∴正方形对角线, .
∴.
∵,
∴,
∴,
∴,
解得,.
故答案为:.
【点睛】本题主要考查了正方形的性质、勾股定理、相似三角形的判定和性质,解题的关键是逐步推导出相关线段的长度.
13. 120
【分析】由点A与点F重合能够得出的长,从而可以求出点A离地面的高度.连接并延长,交于点Q,得到直角三角形,又由使用时四个踏板都是平行于地面且全等的矩形,得到,得到,利用相似三角形的性质可以求出的长,进而利用勾股定理可以求出点A到地面的高度.
【详解】∵将踏板往上收起时(如图2),点A与点F重合,
∴.
∴,
即点A离地面的高度为120 .
如图,连接并延长,交于点Q,则.
∵使用时四个踏板都是平行于地面且全等的矩形,
∴,,
∴,
∴,
即,
解得.
在中,由勾股定理,得
,
即点A到地面的高度是.
故答案为:120,.
【点睛】本题是一道实际应用题,主要考查了相似三角形的判定与性质、等腰三角形的性质、勾股定理等知识,正确理解题意,能够将实际问题转化成数学问题是解题的关键.
14.
【分析】连接交于,根据坐标系求出点的坐标,再根据位似中心的概念解答即可.
【详解】解:连接交于,则点为位似中心,
设的解析式为:,将,,
代入可得:,解得:,
∴的解析式为:,
当时,
∴点的坐标为,
则位似中心的坐标为,
故答案为:.
【点睛】本题考查的是位似变换,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.还考查了待定系数法求一次函数解析式.
15.(1)
(2)
【分析】(1)设,则,再结合题意可列出关于k的等式,解出k的值,即可求出线段a,b,c的长;
(2)由题意可直接得出,解出x的值(舍去负值)即可.
【详解】(1)由题意可设,则,
∵,
∴,
解得:,
∴;
(2)∵,
∴,
整理,得:,
解得:(舍去负值).
【点睛】本题考查比例的性质,比例中项的概念.利用“设k法”是解题关键.
16.(1)①②为条件,③为结论,证明见解析
(2).
【分析】(1)①②为条件,③为结论,利用角平分线的定义、平行线的性质证明,再利用等边对等角即可得出结论;
(2)利用勾股定理求得,作于点H,利用角平分线的性质得到,证明和,推出,再根据平行线分线段成比例定理即可求解.
【详解】(1)解:①是的角平分线,②为条件,③为结论,
证明:∵是的角平分线,
∴,
∵,
∴,
∴,
∴;
(2)解:∵四边形是正方形,且,∴,,
∴,
作于点H,连接,
∵是的角平分线,,
∴,
又∵,
∴,
∴,
∴,
∴,
又∵,
∴,
∴,
∴,
∵,
∴,
∴.
【点睛】本题考查了正方形的性质,角平分线的性质,全等三角形的判定和性质,平行线分线段成比例定理,勾股定理等,解题的关键是灵活运用所学知识解决问题.
17.见解析
【分析】根据,得出,进而可得出结论.
【详解】证明:∵,
∴,
∴,
∵,
∴.
【点睛】本题考查相似三角形的判定,掌握相似三角形的判定定理是解题的关键.
18.(1)见解析
(2)
【分析】根据正方形的性质可得,,,得出,根据,则,即可证明;
(2)先根据勾股定理求得的长,然后根据相似三角形的性质即可求解.
【详解】(1)解:证明:∵四边形是正方形,
∴,,,
∴,
又∵,
∴,
∴,
∴;
(2)∵,,,
∴,
∵是的中点,
∴,
∵,
∴,即,
∴.
【点睛】本题考查了正方形的性质,相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.
19.(1)作图见详解,
(2)作图见详解,
【分析】(1)根据轴对称的性质作图即可,再结合网格坐标,可得出的坐标;
(2)根据与的相似比为,且这两个三角形在点同侧,连接并延长至D点,使得,连接并延长至E点,使得,连接并延长至F点,使得,依次连接D、E、F点即可得,问题随之得解.
【详解】(1)如图,
即为所求,
结合图形,点的对应点的坐标为:;
(2)如图,
即为所求,
结合图形,点的对应点的坐标.
【点睛】本题主要考查了画位似图形、轴对称图形等知识,理解位似图形的性质是解答本题的关键.
20.(1)
(2)秒或秒
【分析】(1)根据已知求出、和,再根据同位角相等求出,根据成比例线段求出长度;
(2)设经过秒后,以、、为顶点的三角形与相似,则,,利用三角形相似对应边成比例,分成和两种情况求解即可.
【详解】(1)解:由题意得:,,,
,
,
,即,
解得,
条幅的长度为;
(2)设经过秒后,以、、为顶点的三角形与相似,则,,
当时,,即,
解得,
当时,,即,
解得,
∴经过秒或秒后,以、、为顶点的三角形与相似.
【点睛】本题考查了相似三角形的应用,平行线的判定,平行线分线段成比例,熟练掌握并灵活运用这些性质是解答本题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
第二十五章 图形的相似 单元练习 2023-2024学年 冀教版(2012)九年级数学上册(含解析)
一、单选题
1.(2022秋·辽宁丹东·九年级统考期末)如图,点是线段的黄金分割点,且,下列选项错误的是( )
A. B.
C. D.
2.(2022秋·安徽六安·九年级校考期末)如图,,两条直线与这三条平行线分别交于点A、、和、、,若,则的值为( )
A. B. C. D.
3.(2022秋·浙江舟山·九年级统考期末)如图,在△ABC中,EF//BC,EG//AB,则下列式子一定正确的是( )
A. B.
C. D.
4.(2022秋·山西临汾·九年级统考期末)如图,每个小正方形边长均为1,则图中的三角形中与相似的是( )
A. B. C. D.
5.(2023秋·海南海口·九年级统考期末)如图,在中,是的中点,,若的面积为4,则四边形的面积为( )
A.8 B.10 C.12 D.16
6.(2023秋·江西萍乡·九年级统考期末)如图,圆桌上方的灯泡(看作一个点)发出的光线照射桌面后,在地面形成阴影,已知桌面的直径为,桌面距离地面,若灯泡距离地面,则地面上阴影部分面积为( )
A. B. C. D.
7.(2020秋·广东揭阳·九年级统考期末)如图,,,分别是,,的中点,下面的说法中:①与是位似图形;②与的相似比为;③与的周长之比为;④与的面积之比为.正确的是( )
A.①②③ B.①③④ C.①②④ D.②③④
二、填空题
8.(2023秋·山东青岛·九年级统考期末)已知,则的值为 .
9.(2023春·黑龙江大庆·九年级校考期末)如图,是的中线,点E在边上,交于点F,若,,则的长度为 cm.
10.(2018秋·江苏泰州·九年级校联考期末)如图,△ABC中,AE交BC于点D,∠CAE=∠CBE,AD:DE=2:3,AE=15,BD=8,则DC的长等于 .
11.(2022秋·湖南益阳·九年级校联考期末)如图D,E两点分别在线段和上,在下列四个条件中:①;②;③;④.其中能使与相似的是 .(填序号)
12.(2023秋·河南驻马店·九年级统考期末)如图,在正方形中,与相交于点O,的平分线分别交于M、N两点.若,则线段的长为 .
13.(2022秋·浙江湖州·九年级统考期末)如图1是一个家用折叠梯子,使用时四个踏板都是平行于地面且全等的矩形,已知踏板宽,,将踏板往上收起时(如图2),点A与点F重合,此时,踏板可以看作与支架重合,将梯子垂直摆放时,点A离地面的高度为 .图3是图1的简略视图,若点H恰好在点A的正下方,此时点A到地面的高度是 .
14.(2023秋·山西·九年级校联考期末)如图,在平面直角坐标系中,与是位似图形,它们顶点的横坐标、纵坐标都是整数,则位似中心的坐标为 .
三、解答题
15.(2022秋·安徽蚌埠·九年级校考期末)已知a,b,c为的三边长,且,.
(1)求线段a,b,c的长;
(2)若线段x是线段a,b的比例中顶(即),求线段x的长.
16.(2023秋·广东佛山·九年级统考期末)如图,在边长为4的正方形中,点E在边上,且,连接,点F、G分别在、上.
(1)给定三个关系:①是的角平分线,②,③,从中选择两个作为条件,一个作为结论构成一个真命题,并说明理由;
(2)在(1)的条件下,求线段的长度.
17.(2023秋·安徽六安·九年级校考期末)如图,与中,,;证明:.
18.(2023秋·河北唐山·九年级统考期末)如图,正方形中,为上一点,是的中点,,垂足为,交的延长线于点,交于点.
(1)求证:;
(2)若,,求的长.
19.(2023秋·山西长治·九年级统考期末)如图,点和在平面直角坐标系中,点的坐标是,根据下列要求,解答相应的问题:
(1)作关于轴对称的,直接写出点的对应点的坐标;
(2)作关于点成位似中心的位似,与的相似比为,且这两个三角形在点同侧,直接写出点的对应点的坐标.
20.(2022秋·广东梅州·九年级统考期末)北京时间年月日时分,神舟十五号载人飞船成功发射,为弘扬航天精神,某校在教学楼上悬挂了一幅励志条幅(即).小亮同学想知道条幅的长度,他的测量过程如下:如图,刚开始他站在距离教学楼的点处,在点正上方点处测得,然后向教学楼条幅方向前行到达点处,在点正上方点处测得,若,,均为,的长为.
(1)如图1,请你帮助小亮计算条幅长度
(2)若小亮从点开始以每秒的速度向点行走至(正上方点),经过多少秒后,以、、为顶点的三角形与相似.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】根据黄金分割的定义得,即可解决问题.
【详解】解:点是线段的黄金分割点,且,
,
,,
A、C、D选项不符合题意,
故选:B.
【点睛】本题考查了黄金分割,解题的关键是掌握黄金分割的定义:把一条线段分割为两部分,使较大部分与全长的比值等于较小部分与较大的比值,这个比值为,近似值为,即为黄金分割.
2.A
【分析】根据平行线分线段成比例定理得到,根据合比性质即得.
【详解】,
,
.
故选:A.
【点睛】本题主要考查了平行线分线段,解决问题的关键是熟练掌握平行线分线段成比例定理,合比性质.
3.D
【分析】根据平行线分线段成比例定理逐一判断即可.
【详解】∵EG//AB,EF//BC,
∴,
∵AC≠EC
∴不成立,
∴选项A错误;
∵EG//AB,EF//BC,
∴,,
∵AE≠EC,
∴不成立,
∴选项B错误;
∵EG//AB,EF//BC,
∴,
∵DF≠AF
∴不成立,
∴选项C错误;
∵EG//AB,EF//BC,
∴,,
∴,
∴选项D正确;
故选D.
【点睛】本题考查了平行线分线段成比例定理,熟练掌握定理,特别是比例中对应线段的属性保持一致是解题的关键.
4.B
【分析】直接利用相似三角形的判定方法结合正方形的性质分析得出答案.
【详解】解:由题意可得:,,
,,,,
,,
,
又,
.
故选:B.
【点睛】此题主要考查了相似三角形的判定,正确得出对应边的关系是解题关键.
5.C
【分析】根据相似三角形的性质得出的面积,即可求出答案.
【详解】解:∵点D是的中点,
∴
∵
∴,
∴,
∴
∴四边形的面积为,
故选:C.
【点睛】本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定.
6.D
【分析】欲求投影圆的面积,可先求出其直径,而直径可通过构造相似三角形,由相似三角形性质求出.
【详解】解:构造几何模型如图:
依题意知,,
∴,
∴,即,
∴,
∴ ,
故选:D.
【点睛】本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力.利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
7.B
【分析】根据位似图形的性质,得出①与是位似图形,进而根据位似图形一定是相似图形得出 ②与是相似图形,再根据周长比等于位似比,以及根据面积比等于相似比的平方,即可得出答案.
【详解】解:根据位似性质得出:
①与是位似图形,
②与是相似图形,且相似比是:,
③与的周长比等于相似比,即,
④根据面积比等于相似比的平方,则与的面积比为.
综上所述,正确的结论是:①③④.
故选:B.
【点睛】本题考查了位似的相关知识,位似是相似的特殊形式,位似比等于相似比,其对应的面积比等于相似比的平方.
8./
【分析】先求出,再根据比例的性质即可得.
【详解】解:,
,
,
故答案为:.
【点睛】本题考查了比例的性质,熟练掌握比例的性质是解题关键.
9.1.2
【分析】过D点作交于G点,如图,利用得到,则,所以,再利用得到,然后利用比例的性质求.
【详解】解:过D点作交于G点,如图,
∵是的中线,
∴,
∵,
∴,
∵,
∴,即,
∴,
∵,
∴,
∴,
∴.
故答案为1.2.
【点睛】本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.作为解题的关键.
10..
【分析】根据相似三角形的性质与判定即可求出答案.
【详解】解:由题意可知AD:DE=2:3,AE=15,
∴AD=6,DE=9,
∵∠CAE=∠CBE,∠BDE=∠ADE,
∴△BDE∽△ADC,
∴,
∴,
∴CD=,
故答案为.
【点睛】本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于中等题型.
11.①②③
【分析】根据相似三角形的判定定理逐个排查即可.
【详解】解:∵,
∴根据 “两个三角形的两个角分别对应相等,则三角形相似”可证,故①满足题意;
∵,
∴根据 “两个三角形的两个角分别对应相等,则三角形相似”可证,故②满足题意;
∵
∴
∴根据 “两边对应成比例且夹角相等,两个三角形相似”可证,故③满足题意;
∵,而与不一定相等,故④不满足题意,
∴综上可得:①②③符合题意.
故答案为①②③.
【点睛】本题主要考查了相似三角形的判定,灵活运用相似三角形的判定定理是解答本题的关键.
12.
【分析】过M点作,根据等腰直角三角形的性质求出长,再根据角平分线性质可得长,由此得到正方形的边长,求出和长,根据得到,得出,从而可求长.
【详解】解:过M点作,
∵四边形是正方形,是对角线,
∴,
∴,,
∴.
∵平分,
∴.
∴正方形边长,
∴正方形对角线, .
∴.
∵,
∴,
∴,
∴,
解得,.
故答案为:.
【点睛】本题主要考查了正方形的性质、勾股定理、相似三角形的判定和性质,解题的关键是逐步推导出相关线段的长度.
13. 120
【分析】由点A与点F重合能够得出的长,从而可以求出点A离地面的高度.连接并延长,交于点Q,得到直角三角形,又由使用时四个踏板都是平行于地面且全等的矩形,得到,得到,利用相似三角形的性质可以求出的长,进而利用勾股定理可以求出点A到地面的高度.
【详解】∵将踏板往上收起时(如图2),点A与点F重合,
∴.
∴,
即点A离地面的高度为120 .
如图,连接并延长,交于点Q,则.
∵使用时四个踏板都是平行于地面且全等的矩形,
∴,,
∴,
∴,
即,
解得.
在中,由勾股定理,得
,
即点A到地面的高度是.
故答案为:120,.
【点睛】本题是一道实际应用题,主要考查了相似三角形的判定与性质、等腰三角形的性质、勾股定理等知识,正确理解题意,能够将实际问题转化成数学问题是解题的关键.
14.
【分析】连接交于,根据坐标系求出点的坐标,再根据位似中心的概念解答即可.
【详解】解:连接交于,则点为位似中心,
设的解析式为:,将,,
代入可得:,解得:,
∴的解析式为:,
当时,
∴点的坐标为,
则位似中心的坐标为,
故答案为:.
【点睛】本题考查的是位似变换,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.还考查了待定系数法求一次函数解析式.
15.(1)
(2)
【分析】(1)设,则,再结合题意可列出关于k的等式,解出k的值,即可求出线段a,b,c的长;
(2)由题意可直接得出,解出x的值(舍去负值)即可.
【详解】(1)由题意可设,则,
∵,
∴,
解得:,
∴;
(2)∵,
∴,
整理,得:,
解得:(舍去负值).
【点睛】本题考查比例的性质,比例中项的概念.利用“设k法”是解题关键.
16.(1)①②为条件,③为结论,证明见解析
(2).
【分析】(1)①②为条件,③为结论,利用角平分线的定义、平行线的性质证明,再利用等边对等角即可得出结论;
(2)利用勾股定理求得,作于点H,利用角平分线的性质得到,证明和,推出,再根据平行线分线段成比例定理即可求解.
【详解】(1)解:①是的角平分线,②为条件,③为结论,
证明:∵是的角平分线,
∴,
∵,
∴,
∴,
∴;
(2)解:∵四边形是正方形,且,∴,,
∴,
作于点H,连接,
∵是的角平分线,,
∴,
又∵,
∴,
∴,
∴,
∴,
又∵,
∴,
∴,
∴,
∵,
∴,
∴.
【点睛】本题考查了正方形的性质,角平分线的性质,全等三角形的判定和性质,平行线分线段成比例定理,勾股定理等,解题的关键是灵活运用所学知识解决问题.
17.见解析
【分析】根据,得出,进而可得出结论.
【详解】证明:∵,
∴,
∴,
∵,
∴.
【点睛】本题考查相似三角形的判定,掌握相似三角形的判定定理是解题的关键.
18.(1)见解析
(2)
【分析】根据正方形的性质可得,,,得出,根据,则,即可证明;
(2)先根据勾股定理求得的长,然后根据相似三角形的性质即可求解.
【详解】(1)解:证明:∵四边形是正方形,
∴,,,
∴,
又∵,
∴,
∴,
∴;
(2)∵,,,
∴,
∵是的中点,
∴,
∵,
∴,即,
∴.
【点睛】本题考查了正方形的性质,相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.
19.(1)作图见详解,
(2)作图见详解,
【分析】(1)根据轴对称的性质作图即可,再结合网格坐标,可得出的坐标;
(2)根据与的相似比为,且这两个三角形在点同侧,连接并延长至D点,使得,连接并延长至E点,使得,连接并延长至F点,使得,依次连接D、E、F点即可得,问题随之得解.
【详解】(1)如图,
即为所求,
结合图形,点的对应点的坐标为:;
(2)如图,
即为所求,
结合图形,点的对应点的坐标.
【点睛】本题主要考查了画位似图形、轴对称图形等知识,理解位似图形的性质是解答本题的关键.
20.(1)
(2)秒或秒
【分析】(1)根据已知求出、和,再根据同位角相等求出,根据成比例线段求出长度;
(2)设经过秒后,以、、为顶点的三角形与相似,则,,利用三角形相似对应边成比例,分成和两种情况求解即可.
【详解】(1)解:由题意得:,,,
,
,
,即,
解得,
条幅的长度为;
(2)设经过秒后,以、、为顶点的三角形与相似,则,,
当时,,即,
解得,
当时,,即,
解得,
∴经过秒或秒后,以、、为顶点的三角形与相似.
【点睛】本题考查了相似三角形的应用,平行线的判定,平行线分线段成比例,熟练掌握并灵活运用这些性质是解答本题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
