11.1 与三角形相关的线段 同步练习 人教版数学八年级上册(含答案)
文档属性
| 名称 | 11.1 与三角形相关的线段 同步练习 人教版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 163.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 17:47:21 | ||
图片预览



文档简介
11.1 与三角形相关的线段 同步练习
一、单选题
1.如图,的顶点A,B,C在边长为1的正方形网格的格点上,则边上的高为( )
A. B. C. D.
2.下列每组数据分别是三根木棒的长度,能用它们摆成三角形的是( )
A.,, B.,,
C.,, D.,,
3.三边都不相等的三角形有两边长分别为3和5,第三长是奇数,则其周长为( )
A.15 B.13 C.11 D.15或13或11
4.如图,在△ABC中,AB=AC=5,BC=3,BD为中线,则△ABD与△BCD的周长之差为( )
A.1 B.2 C.3 D.4
5.已知三角形的两边长分别是3cm和7cm,则下列长度的线段中能作为第三边的是( )
A.3cm B.4cm C.7cm D.10cm
6.在下列长度的木棒中,能与4cm、9cm长的两根木棒钉成一个三角形的是( )
A. B. C. D.
7.已知三角形的两边长分别为2cm和3cm,则第三边长可能是( )
A.6cm B.5cm C.3cm D.1cm
8.以下列各组线段为边,能组成三角形的是( )
A. B.
C. D.
二、填空题
9.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0).现将线段AB向上平移2个单位,再向右平移1个单位,得到线段AB的对应线段CD,连接AC,BD.
(1)点D的坐标为 ;
(2)在y轴上存在一点P,连接PA,PB,且S△PAB=2,求出满足条件的所有点P的坐标 .
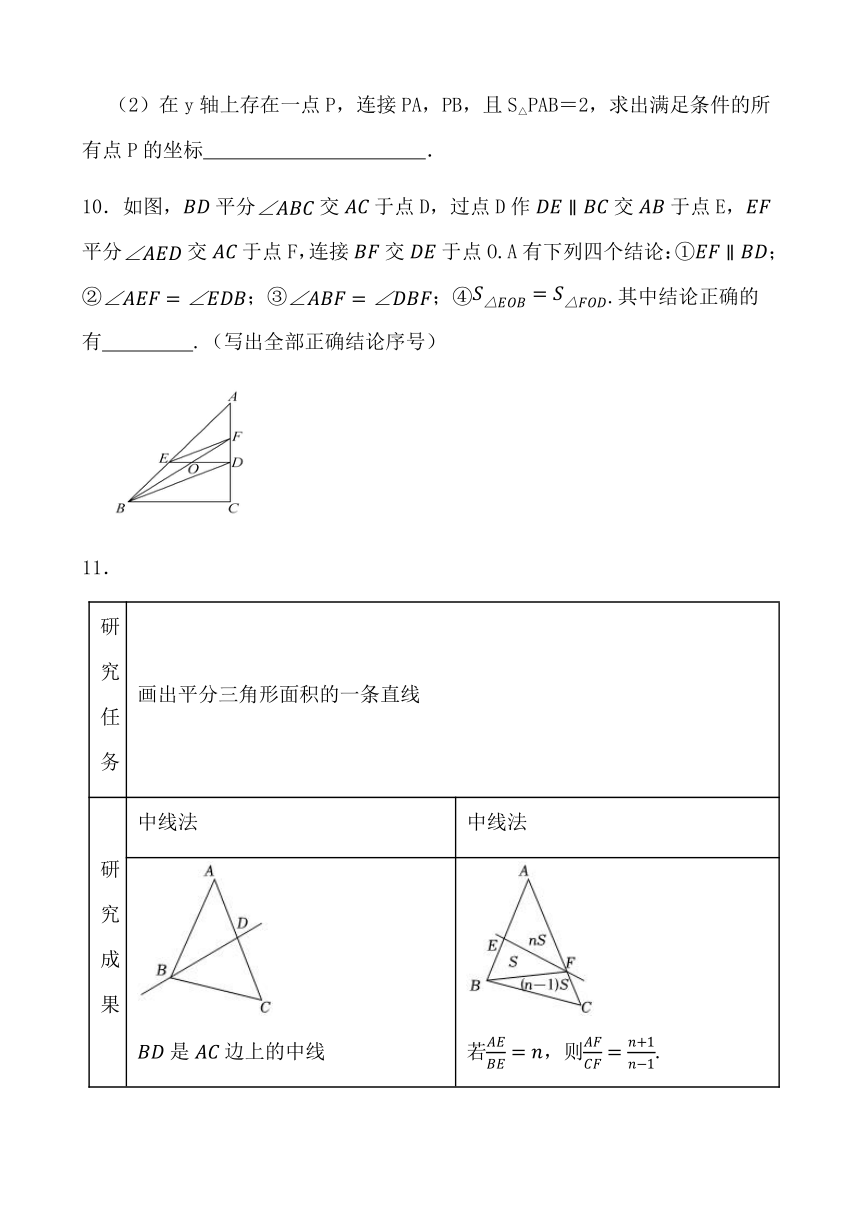
10.如图,平分交于点D,过点D作交于点E,平分交于点F,连接交于点O.A有下列四个结论:①;②;③;④.其中结论正确的有 .(写出全部正确结论序号)
11.
研究任务 画出平分三角形面积的一条直线
研究成果 中线法 中线法
是边上的中线 若,则.
成果应用 如图,在中,是边上的中线,直线平分的面积,交于点已知,的面积为,则 ,四边形的面积为 .
12.如图,A、B、C分别是线段、、的中点,若的面积是1,那么的面积为 .
13.如图,已知在 中,D,E分别为边 , 的中点,且 ,则 等于 .
三、解答题
14.三角形ABC在直角坐标系中,且A(0,4),B(-2,0),C(3,-5),将三角形ABC向下平移2个单位,再向左平移4个单位得到三角形A1B1C1,求三角形A1B1C1的面积。
15.如图,在中,、分别是上的高和中线,,,求的长.
16.如图所示,在△ABC中,AC=5,BC=6,BC边上高AD=4,若点P在边AC上(不含端点)移动,求BP最短时的值.
17.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠EAD的度数.
18.如图,在△ABC中,AD⊥BE,∠DAC=10°,AE是∠BAC的外角∠MAC的平分线,BF平分∠ABC交AE于点F,求∠AFB的度数.
参考答案:
1.B
2.B
3.A
4.B
5.C
6.D
7.C
8.B
9.(1)(4,2)
(2)0,1)或(0,-1)
10.①②④
11.3;
12.7
13.40
14.解:由平移定义可知,平移前后图形形状大小不变,故;
∴=5×9-×3×9-×2×4-×5×5=15.
15.解:∵是边上的中线,
∴是的中点,
∴,
∵,
∴,
∴=.
16.解:根据垂线段最短可知,当BP⊥AC时,BP最短.
∵S△ABCBC×ADAC×BP,
∴6×4=5BP,∴PB,
即BP最短时的值为.
17.解:∵∠BAC=60°,∠C=50°
∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°-90°-∠C=40°,
∵AE是角平分线,
∴∠EAC=30°
∴∠EAD=∠DAC-∠EAC=40°-30°=10°
18.解:∵AD⊥BE,
∴∠ADC=90°,
∵∠DAC=10°,
∴∠ACB=90°﹣∠DAC=90°﹣10°=80°,
∵AE是∠MAC的平分线,BF平分∠ABC,
∴,
又∵∠MAE=∠ABF+∠AFB,∠MAC=∠ABC+∠ACB,
∴∠AFB=∠MAE﹣∠ABF=.
一、单选题
1.如图,的顶点A,B,C在边长为1的正方形网格的格点上,则边上的高为( )
A. B. C. D.
2.下列每组数据分别是三根木棒的长度,能用它们摆成三角形的是( )
A.,, B.,,
C.,, D.,,
3.三边都不相等的三角形有两边长分别为3和5,第三长是奇数,则其周长为( )
A.15 B.13 C.11 D.15或13或11
4.如图,在△ABC中,AB=AC=5,BC=3,BD为中线,则△ABD与△BCD的周长之差为( )
A.1 B.2 C.3 D.4
5.已知三角形的两边长分别是3cm和7cm,则下列长度的线段中能作为第三边的是( )
A.3cm B.4cm C.7cm D.10cm
6.在下列长度的木棒中,能与4cm、9cm长的两根木棒钉成一个三角形的是( )
A. B. C. D.
7.已知三角形的两边长分别为2cm和3cm,则第三边长可能是( )
A.6cm B.5cm C.3cm D.1cm
8.以下列各组线段为边,能组成三角形的是( )
A. B.
C. D.
二、填空题
9.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0).现将线段AB向上平移2个单位,再向右平移1个单位,得到线段AB的对应线段CD,连接AC,BD.
(1)点D的坐标为 ;
(2)在y轴上存在一点P,连接PA,PB,且S△PAB=2,求出满足条件的所有点P的坐标 .
10.如图,平分交于点D,过点D作交于点E,平分交于点F,连接交于点O.A有下列四个结论:①;②;③;④.其中结论正确的有 .(写出全部正确结论序号)
11.
研究任务 画出平分三角形面积的一条直线
研究成果 中线法 中线法
是边上的中线 若,则.
成果应用 如图,在中,是边上的中线,直线平分的面积,交于点已知,的面积为,则 ,四边形的面积为 .
12.如图,A、B、C分别是线段、、的中点,若的面积是1,那么的面积为 .
13.如图,已知在 中,D,E分别为边 , 的中点,且 ,则 等于 .
三、解答题
14.三角形ABC在直角坐标系中,且A(0,4),B(-2,0),C(3,-5),将三角形ABC向下平移2个单位,再向左平移4个单位得到三角形A1B1C1,求三角形A1B1C1的面积。
15.如图,在中,、分别是上的高和中线,,,求的长.
16.如图所示,在△ABC中,AC=5,BC=6,BC边上高AD=4,若点P在边AC上(不含端点)移动,求BP最短时的值.
17.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠EAD的度数.
18.如图,在△ABC中,AD⊥BE,∠DAC=10°,AE是∠BAC的外角∠MAC的平分线,BF平分∠ABC交AE于点F,求∠AFB的度数.
参考答案:
1.B
2.B
3.A
4.B
5.C
6.D
7.C
8.B
9.(1)(4,2)
(2)0,1)或(0,-1)
10.①②④
11.3;
12.7
13.40
14.解:由平移定义可知,平移前后图形形状大小不变,故;
∴=5×9-×3×9-×2×4-×5×5=15.
15.解:∵是边上的中线,
∴是的中点,
∴,
∵,
∴,
∴=.
16.解:根据垂线段最短可知,当BP⊥AC时,BP最短.
∵S△ABCBC×ADAC×BP,
∴6×4=5BP,∴PB,
即BP最短时的值为.
17.解:∵∠BAC=60°,∠C=50°
∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°-90°-∠C=40°,
∵AE是角平分线,
∴∠EAC=30°
∴∠EAD=∠DAC-∠EAC=40°-30°=10°
18.解:∵AD⊥BE,
∴∠ADC=90°,
∵∠DAC=10°,
∴∠ACB=90°﹣∠DAC=90°﹣10°=80°,
∵AE是∠MAC的平分线,BF平分∠ABC,
∴,
又∵∠MAE=∠ABF+∠AFB,∠MAC=∠ABC+∠ACB,
∴∠AFB=∠MAE﹣∠ABF=.
