12.1 全等三角形 同步练习 人教版数学八年级上册(含答案)
文档属性
| 名称 | 12.1 全等三角形 同步练习 人教版数学八年级上册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 143.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 17:50:28 | ||
图片预览



文档简介
12.1 全等三角形 同步练习 2022-2023学年八年级上册人教版数学
一、单选题
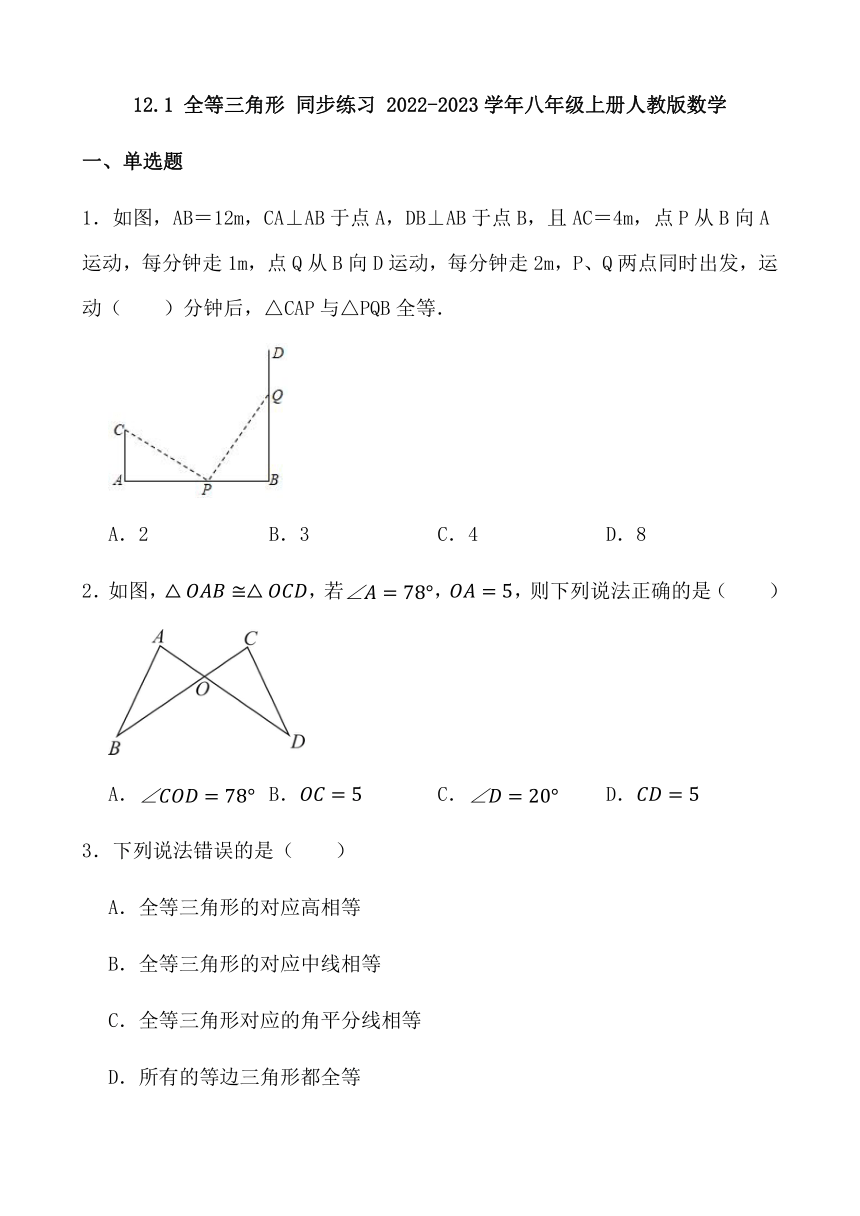
1.如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从B向A运动,每分钟走1m,点Q从B向D运动,每分钟走2m,P、Q两点同时出发,运动( )分钟后,△CAP与△PQB全等.
A.2 B.3 C.4 D.8
2.如图,,若,,则下列说法正确的是( )
A. B. C. D.
3.下列说法错误的是( )
A.全等三角形的对应高相等
B.全等三角形的对应中线相等
C.全等三角形对应的角平分线相等
D.所有的等边三角形都全等
4.下列命题中:①形状相同的两个三角形是全等形;②在两个三角形中,相等的角是对应角,相等的边是对应边;③全等三角形的对应边相等;④全等三角形对应边上的高相等.其中真命题有( )个.
A. B. C. D.
5.下列命题:①三角形的一条中线把这个三角形的面积平分;②三角形的角平分线,中线,高线都在三角形的内部;③全等三角形面积相等,面积相等的三角形也全等;④三角形具有稳定性.其中真命题的个数是( )
A.1 B.2 C.3 D.4
6.下列说法正确的是( )
A.两个面积相等的图形一定是全等图形
B.两个全等图形形状一定相同
C.两个周长相等的图形一定是全等图形
D.两个正三角形一定是全等图形
7.如图,点A,B,C,D在同一条直线上,且,,,若,则的度数为( )
A. B. C. D.
8.如图,在 中,D,E分别是边 , 上的点,若 ,则 的度数为( )
A. B. C. D.
二、填空题
9.如图,已知△ABD≌△ACE,且∠1=45°,∠ADB=95°,则 ∠AEC= ,∠C= .
10.如图,Rt△AOB≌Rt△CDA,且点A、B的坐标分别为(﹣1,0),b(0,2),则点D的坐标是 .
11.如图,在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为 .
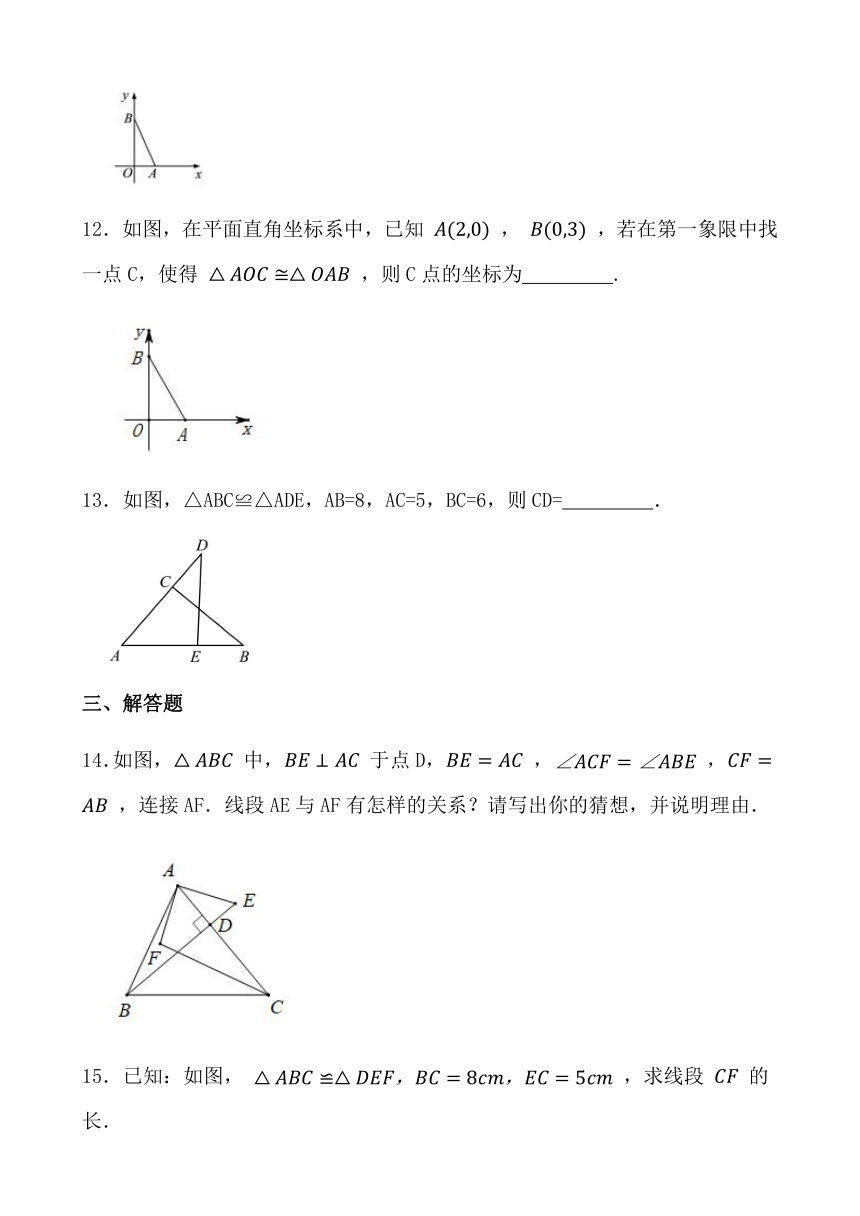
12.如图,在平面直角坐标系中,已知 , ,若在第一象限中找一点C,使得 ,则C点的坐标为 .
13.如图,△ABC≌△ADE,AB=8,AC=5,BC=6,则CD= .
三、解答题
14.如图, 中, 于点D, , , ,连接AF.线段AE与AF有怎样的关系?请写出你的猜想,并说明理由.
15.已知:如图, ,求线段 的长.
16.如图,,点E在线段上,点F在延长线上,,求证:.
17.如图,线段,于点A,,射线于点B,点P从点B向点A运动,每秒走1m,点Q从点B向点D运动,每秒走3m.若点P,Q同时从点B出发,当出发t秒后,在线段MA上有一点C,使以点C,A,P为顶点的三角形与全等,求t的值.
18.如图,△ABE≌△DCE,点A,C,B在一条直线上,∠AED和∠BEC相等吗?为什么?
参考答案:
1.C
2.B
3.D
4.B
5.B
6.B
7.B
8.D
9.95°;50°
10.(﹣3,0)
11.(2,4)或(-2,0)或(-2,4)
12.(2,3)
13.3
14.解: ,
理由如下:
∵ , ,
∴ ≌
∴ ,
∵ 于D,
∴ ,
∴ ,
∴ ,即 ,
∴ .
15.解:∵ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ .
16.证明: ,
,
17.解:当△APC≌△BQP时,AP=BQ,即20-t=3t,
解得:t=5;
当△APC≌△BPQ时,AP=BP=AB=10m,
此时所用时间为10秒,AC=BQ=10m,不合题意,舍去;
综上,出发5秒后,在线段MA上有一点C,使以点C,A,P为顶点的三角形与△PBQ全等.
18.解:相等;
理由:
∵△ABE≌△DCE,
∴∠AEB=∠DEC,
∴∠DEC-∠AEC=∠AEB-∠AEC,
即:∠AED=∠BEC.
一、单选题
1.如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从B向A运动,每分钟走1m,点Q从B向D运动,每分钟走2m,P、Q两点同时出发,运动( )分钟后,△CAP与△PQB全等.
A.2 B.3 C.4 D.8
2.如图,,若,,则下列说法正确的是( )
A. B. C. D.
3.下列说法错误的是( )
A.全等三角形的对应高相等
B.全等三角形的对应中线相等
C.全等三角形对应的角平分线相等
D.所有的等边三角形都全等
4.下列命题中:①形状相同的两个三角形是全等形;②在两个三角形中,相等的角是对应角,相等的边是对应边;③全等三角形的对应边相等;④全等三角形对应边上的高相等.其中真命题有( )个.
A. B. C. D.
5.下列命题:①三角形的一条中线把这个三角形的面积平分;②三角形的角平分线,中线,高线都在三角形的内部;③全等三角形面积相等,面积相等的三角形也全等;④三角形具有稳定性.其中真命题的个数是( )
A.1 B.2 C.3 D.4
6.下列说法正确的是( )
A.两个面积相等的图形一定是全等图形
B.两个全等图形形状一定相同
C.两个周长相等的图形一定是全等图形
D.两个正三角形一定是全等图形
7.如图,点A,B,C,D在同一条直线上,且,,,若,则的度数为( )
A. B. C. D.
8.如图,在 中,D,E分别是边 , 上的点,若 ,则 的度数为( )
A. B. C. D.
二、填空题
9.如图,已知△ABD≌△ACE,且∠1=45°,∠ADB=95°,则 ∠AEC= ,∠C= .
10.如图,Rt△AOB≌Rt△CDA,且点A、B的坐标分别为(﹣1,0),b(0,2),则点D的坐标是 .
11.如图,在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为 .
12.如图,在平面直角坐标系中,已知 , ,若在第一象限中找一点C,使得 ,则C点的坐标为 .
13.如图,△ABC≌△ADE,AB=8,AC=5,BC=6,则CD= .
三、解答题
14.如图, 中, 于点D, , , ,连接AF.线段AE与AF有怎样的关系?请写出你的猜想,并说明理由.
15.已知:如图, ,求线段 的长.
16.如图,,点E在线段上,点F在延长线上,,求证:.
17.如图,线段,于点A,,射线于点B,点P从点B向点A运动,每秒走1m,点Q从点B向点D运动,每秒走3m.若点P,Q同时从点B出发,当出发t秒后,在线段MA上有一点C,使以点C,A,P为顶点的三角形与全等,求t的值.
18.如图,△ABE≌△DCE,点A,C,B在一条直线上,∠AED和∠BEC相等吗?为什么?
参考答案:
1.C
2.B
3.D
4.B
5.B
6.B
7.B
8.D
9.95°;50°
10.(﹣3,0)
11.(2,4)或(-2,0)或(-2,4)
12.(2,3)
13.3
14.解: ,
理由如下:
∵ , ,
∴ ≌
∴ ,
∵ 于D,
∴ ,
∴ ,
∴ ,即 ,
∴ .
15.解:∵ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ .
16.证明: ,
,
17.解:当△APC≌△BQP时,AP=BQ,即20-t=3t,
解得:t=5;
当△APC≌△BPQ时,AP=BP=AB=10m,
此时所用时间为10秒,AC=BQ=10m,不合题意,舍去;
综上,出发5秒后,在线段MA上有一点C,使以点C,A,P为顶点的三角形与△PBQ全等.
18.解:相等;
理由:
∵△ABE≌△DCE,
∴∠AEB=∠DEC,
∴∠DEC-∠AEC=∠AEB-∠AEC,
即:∠AED=∠BEC.
