2022-2023学年人教版数学八年级上册 12.2 三角形全等的判定 同步练习 (含答案)
文档属性
| 名称 | 2022-2023学年人教版数学八年级上册 12.2 三角形全等的判定 同步练习 (含答案) | 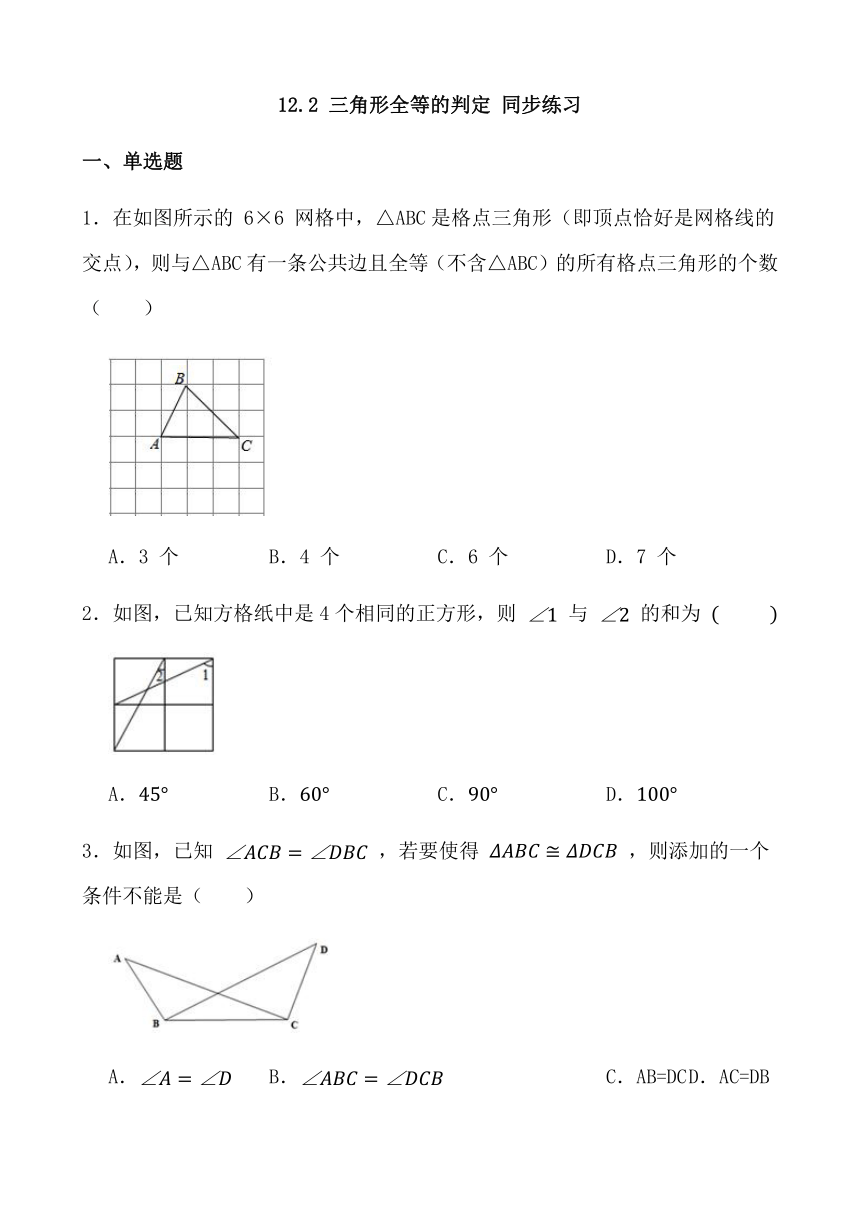 | |
| 格式 | docx | ||
| 文件大小 | 187.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 20:00:30 | ||
图片预览




文档简介
12.2 三角形全等的判定 同步练习
一、单选题
1.在如图所示的 6×6 网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且全等(不含△ABC)的所有格点三角形的个数( )
A.3 个 B.4 个 C.6 个 D.7 个
2.如图,已知方格纸中是4个相同的正方形,则 与 的和为
A. B. C. D.
3.如图,已知 ,若要使得 ,则添加的一个条件不能是( )
A. B. C.AB=DC D.AC=DB
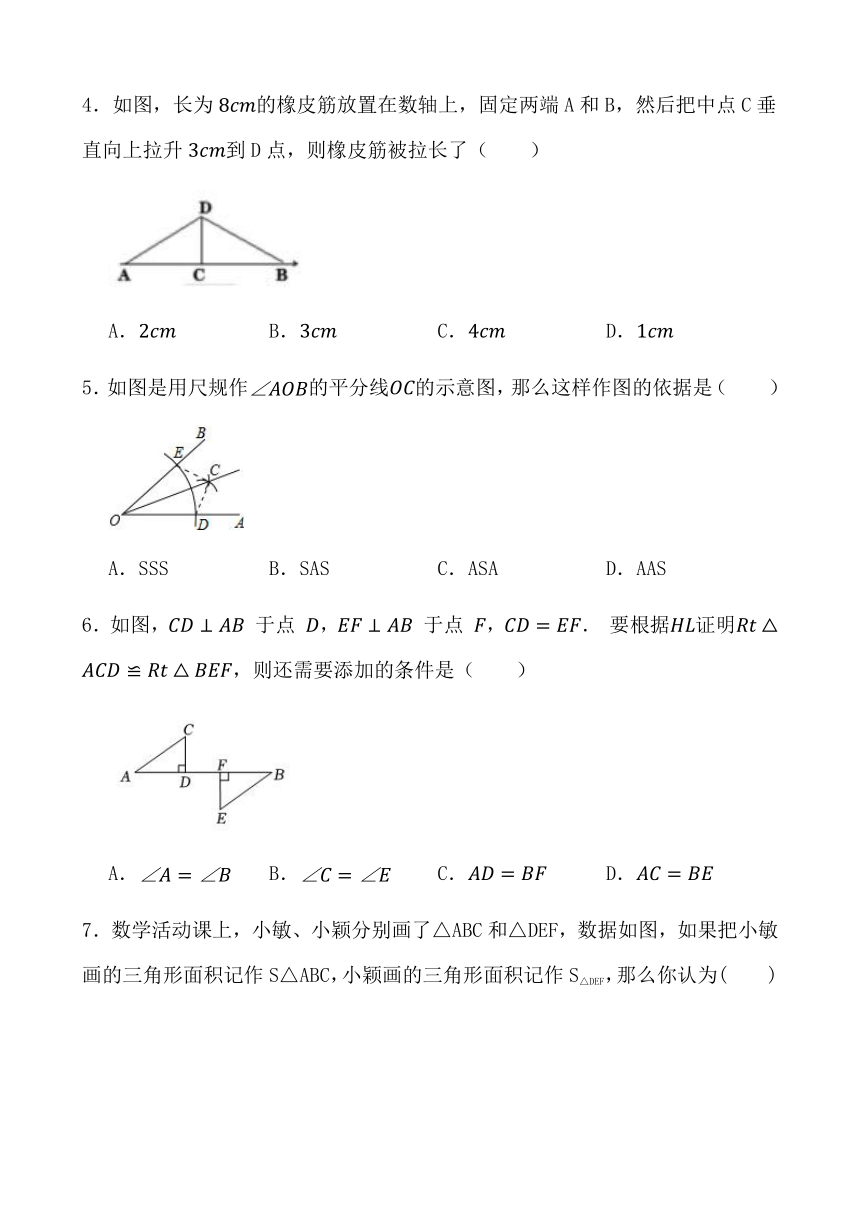
4.如图,长为的橡皮筋放置在数轴上,固定两端A和B,然后把中点C垂直向上拉升到D点,则橡皮筋被拉长了( )
A. B. C. D.
5.如图是用尺规作的平分线的示意图,那么这样作图的依据是( )
A.SSS B.SAS C.ASA D.AAS
6.如图, 于点 , 于点 ,. 要根据证明,则还需要添加的条件是( )
A. B. C. D.
7.数学活动课上,小敏、小颖分别画了△ABC和△DEF,数据如图,如果把小敏画的三角形面积记作S△ABC,小颖画的三角形面积记作S△DEF,那么你认为( )
A.S△ABC >S△DEF B.S△ABCC.S△ABC =S△DEF D.不能确定
8.如图,在△DEC和△BFA中,点A,E,F,C在同一直线上,已知AB∥CD,且AB=CD,若利用“ASA”证明△DEC≌△BFA,则需添加的条件是( )
A.EC=FA B.∠A=∠C C.∠D=∠B D.BF=DE
二、填空题
9.在Rt△ABC中,∠C=90°,AC=15cm,BC=8cm,AX⊥AC于A,P、Q两点分别在边AC和射线AX上移动.当PQ=AB,AP= 时,△ABC和△APQ全等.
10.如图,中,,,是的中点,的取值范围为 .
11.如图,在中,,,平分,于E,若,则为 .
12.在与中,,那么 .
13.如图,是等腰三角形,点,分别在腰,上,且,,连接,交于点.则:
(1)图中有 对全等三角形;
(2)若点恰好为的中点,且的面积为2,则四边形的面积为 .
三、解答题
14.已知:如图,点在同一条直线上,.求证:.
15.如图,AB=CD, BF⊥AC, DE⊥AC, AE=CF.求证:BD平分EF.
16.如图,点D为锐角∠ABC的平分线上一点,点M在边BA上,点N在边BC上,∠BMD+∠BND=180°.试说明:DM=DN.
17.如图,点 在一条直线上, ,求证: .
18.如图,求证:.
参考答案:
1.D
2.C
3.C
4.A
5.A
6.D
7.C
8.C
9.8cm或15cm
10.
11.4
12.
13.(1)3
(2)6
14.证明:∵,
∴,即,
在与中,
,
∴,
∴.
15.证明:∵AE=CF,∴AE+EF=CF+EF,即AF=CE,
在Rt△ABF和Rt△CDE中,
AB=CD
AF=CE
∴Rt△ABF≌Rt△CDE(HL),
∴DE=BF,
在△DEO和△BFO中,
∠EOD=∠FOB
∠DEO=∠BFO=90°
DE=BF
∴△DEO≌△BFO(AAS),
∴EO=FO,
∴BD平分EF.
16.解:过点D作DE⊥AB于点E,DF⊥BC于点F.
∴∠DEB=∠DFB=90°.
又∵BD平分∠ABC,
∴DE=DF.
∵∠BMD+∠DME=180°,∠BMD+∠BND=180°,
∴∠DME=∠BND.
在△EMD和△FND中,
,
∴△EMD≌△FND(AAS).
∴DM=DN.
17.证明:
∴ 即
在△ABE和△DCF中 ∴△ABE≌△DCF.
∴
18.解: ,
,
即 .
在 和 中,
,
≌ ,
.
一、单选题
1.在如图所示的 6×6 网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且全等(不含△ABC)的所有格点三角形的个数( )
A.3 个 B.4 个 C.6 个 D.7 个
2.如图,已知方格纸中是4个相同的正方形,则 与 的和为
A. B. C. D.
3.如图,已知 ,若要使得 ,则添加的一个条件不能是( )
A. B. C.AB=DC D.AC=DB
4.如图,长为的橡皮筋放置在数轴上,固定两端A和B,然后把中点C垂直向上拉升到D点,则橡皮筋被拉长了( )
A. B. C. D.
5.如图是用尺规作的平分线的示意图,那么这样作图的依据是( )
A.SSS B.SAS C.ASA D.AAS
6.如图, 于点 , 于点 ,. 要根据证明,则还需要添加的条件是( )
A. B. C. D.
7.数学活动课上,小敏、小颖分别画了△ABC和△DEF,数据如图,如果把小敏画的三角形面积记作S△ABC,小颖画的三角形面积记作S△DEF,那么你认为( )
A.S△ABC >S△DEF B.S△ABC
8.如图,在△DEC和△BFA中,点A,E,F,C在同一直线上,已知AB∥CD,且AB=CD,若利用“ASA”证明△DEC≌△BFA,则需添加的条件是( )
A.EC=FA B.∠A=∠C C.∠D=∠B D.BF=DE
二、填空题
9.在Rt△ABC中,∠C=90°,AC=15cm,BC=8cm,AX⊥AC于A,P、Q两点分别在边AC和射线AX上移动.当PQ=AB,AP= 时,△ABC和△APQ全等.
10.如图,中,,,是的中点,的取值范围为 .
11.如图,在中,,,平分,于E,若,则为 .
12.在与中,,那么 .
13.如图,是等腰三角形,点,分别在腰,上,且,,连接,交于点.则:
(1)图中有 对全等三角形;
(2)若点恰好为的中点,且的面积为2,则四边形的面积为 .
三、解答题
14.已知:如图,点在同一条直线上,.求证:.
15.如图,AB=CD, BF⊥AC, DE⊥AC, AE=CF.求证:BD平分EF.
16.如图,点D为锐角∠ABC的平分线上一点,点M在边BA上,点N在边BC上,∠BMD+∠BND=180°.试说明:DM=DN.
17.如图,点 在一条直线上, ,求证: .
18.如图,求证:.
参考答案:
1.D
2.C
3.C
4.A
5.A
6.D
7.C
8.C
9.8cm或15cm
10.
11.4
12.
13.(1)3
(2)6
14.证明:∵,
∴,即,
在与中,
,
∴,
∴.
15.证明:∵AE=CF,∴AE+EF=CF+EF,即AF=CE,
在Rt△ABF和Rt△CDE中,
AB=CD
AF=CE
∴Rt△ABF≌Rt△CDE(HL),
∴DE=BF,
在△DEO和△BFO中,
∠EOD=∠FOB
∠DEO=∠BFO=90°
DE=BF
∴△DEO≌△BFO(AAS),
∴EO=FO,
∴BD平分EF.
16.解:过点D作DE⊥AB于点E,DF⊥BC于点F.
∴∠DEB=∠DFB=90°.
又∵BD平分∠ABC,
∴DE=DF.
∵∠BMD+∠DME=180°,∠BMD+∠BND=180°,
∴∠DME=∠BND.
在△EMD和△FND中,
,
∴△EMD≌△FND(AAS).
∴DM=DN.
17.证明:
∴ 即
在△ABE和△DCF中 ∴△ABE≌△DCF.
∴
18.解: ,
,
即 .
在 和 中,
,
≌ ,
.
