2022-2023学年人教版数学八年级上册 12.3 角的平分线的性质 同步练习 (含答案)
文档属性
| 名称 | 2022-2023学年人教版数学八年级上册 12.3 角的平分线的性质 同步练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 181.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 00:00:00 | ||
图片预览


文档简介
12.3 角的平分线的性质 同步练习
一、单选题
1.如图, 平分 交 于点D, 于点E, 于点F.若 , , ,则 的长是( )
A.8 B.7 C.6 D.5
2.如图,点P是∠AOC的角平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最小值为( )
A.2 B.3 C.4 D.5
3.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于D.若BC=32,且CD∶BD=7∶9,则点D到边AB的距离为( )
A.7 B.9 C.14 D.18
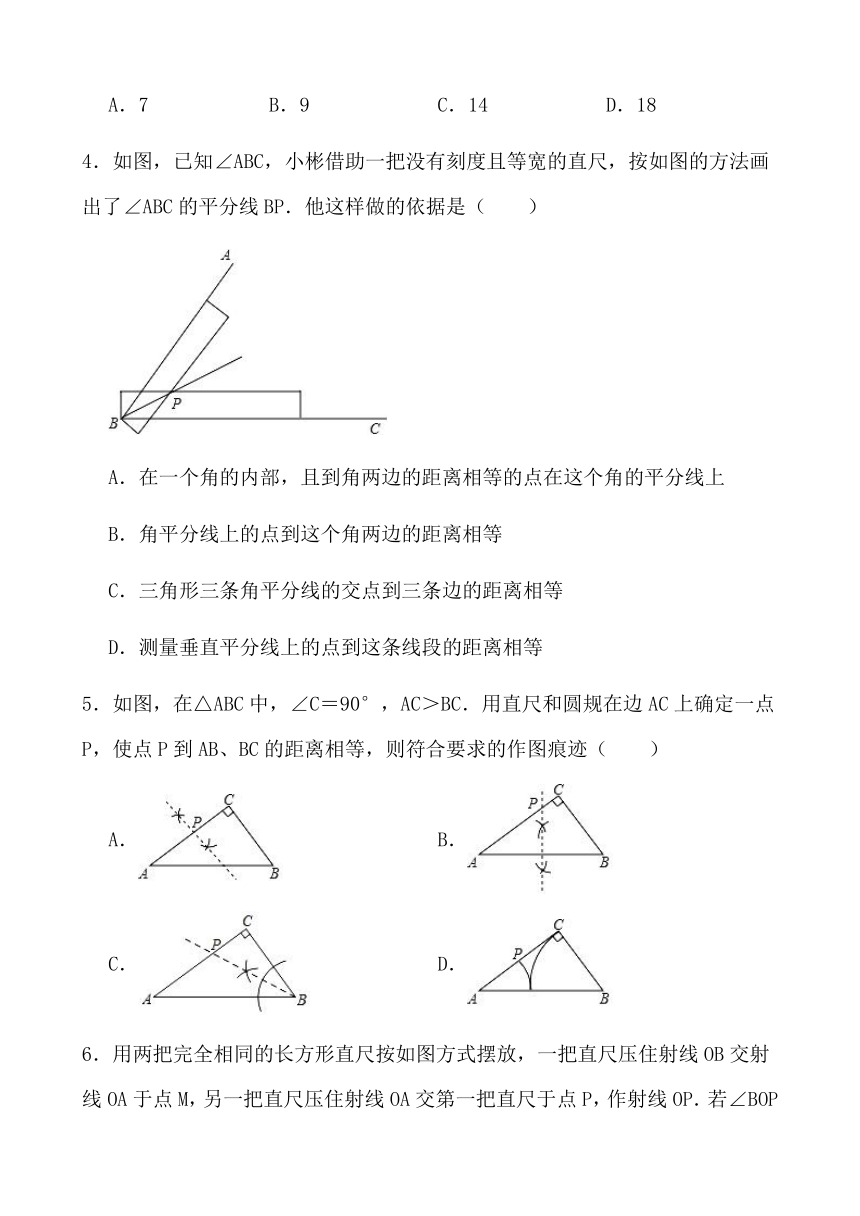
4.如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是( )
A.在一个角的内部,且到角两边的距离相等的点在这个角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.测量垂直平分线上的点到这条线段的距离相等
5.如图,在△ABC中,∠C=90°,AC>BC.用直尺和圆规在边AC上确定一点P,使点P到AB、BC的距离相等,则符合要求的作图痕迹( )
A. B.
C. D.
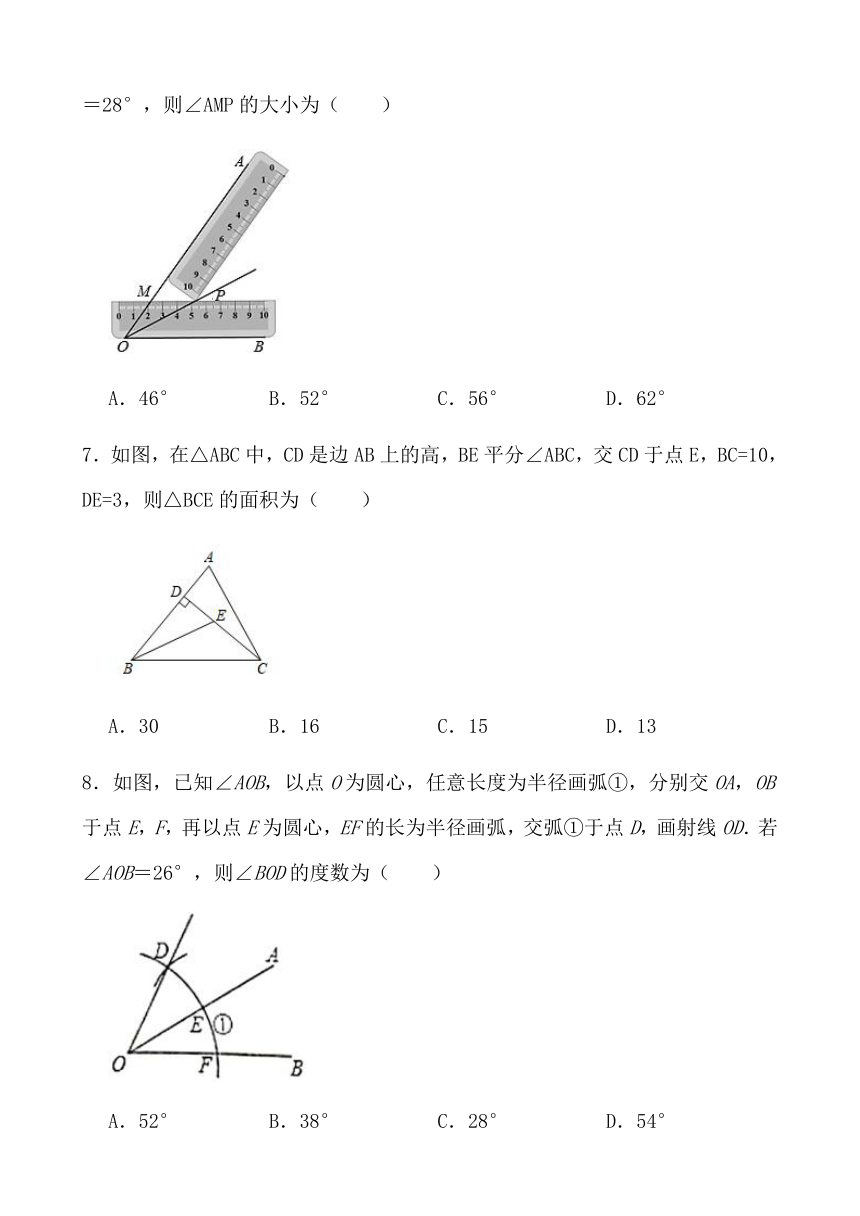
6.用两把完全相同的长方形直尺按如图方式摆放,一把直尺压住射线OB交射线OA于点M,另一把直尺压住射线OA交第一把直尺于点P,作射线OP.若∠BOP=28°,则∠AMP的大小为( )
A.46° B.52° C.56° D.62°
7.如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=10,DE=3,则△BCE的面积为( )
A.30 B.16 C.15 D.13
8.如图,已知∠AOB,以点O为圆心,任意长度为半径画弧①,分别交OA,OB于点E,F,再以点E为圆心,EF的长为半径画弧,交弧①于点D,画射线OD.若∠AOB=26°,则∠BOD的度数为( )
A.52° B.38° C.28° D.54°
二、填空题
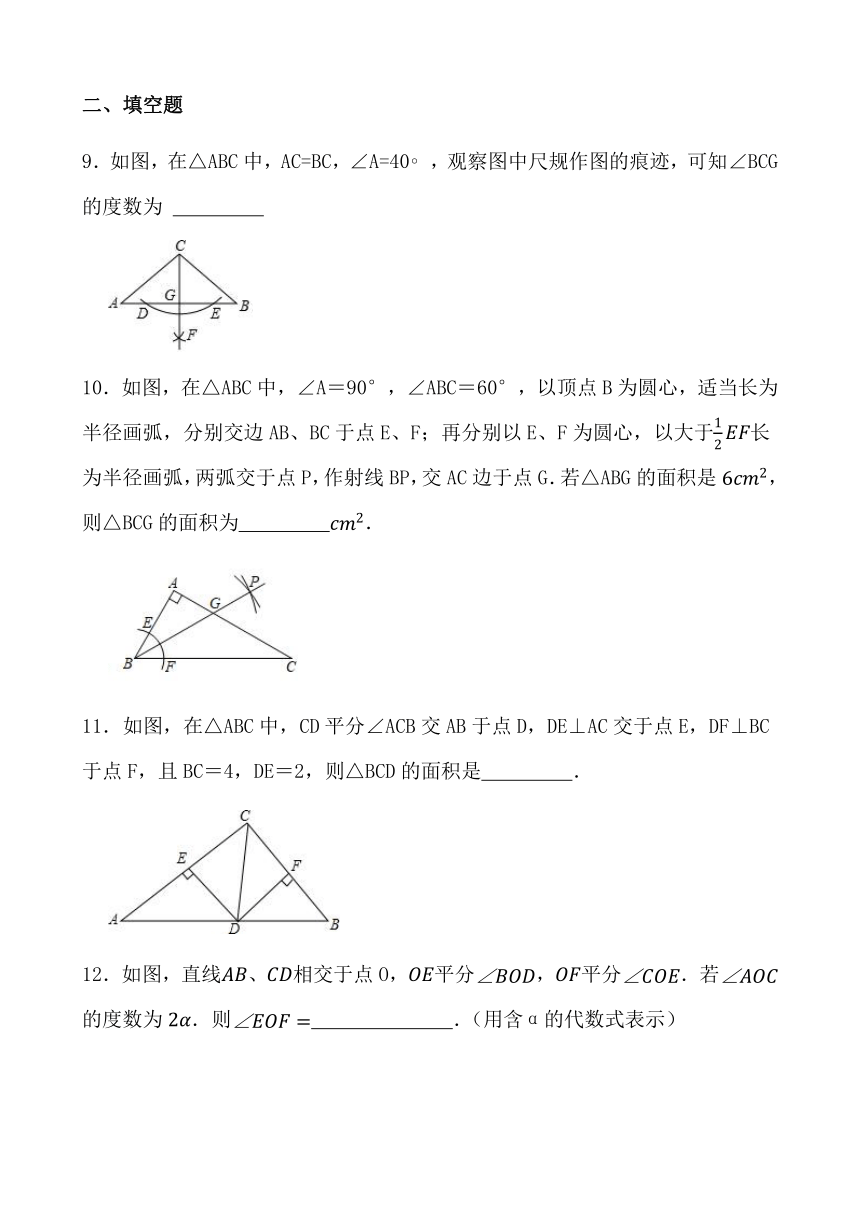
9.如图,在△ABC中,AC=BC,∠A=40 ,观察图中尺规作图的痕迹,可知∠BCG的度数为
10.如图,在△ABC中,∠A=90°,∠ABC=60°,以顶点B为圆心,适当长为半径画弧,分别交边AB、BC于点E、F;再分别以E、F为圆心,以大于长为半径画弧,两弧交于点P,作射线BP,交AC边于点G.若△ABG的面积是,则△BCG的面积为 .
11.如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是 .
12.如图,直线、相交于点O,平分,平分.若的度数为.则 .(用含α的代数式表示)
13.如图,在中,,分别是和的角平分线,过点作于点已知,的周长为,则的面积为 .
三、解答题
14.如图所示,已知BD为∠ABC的平分线,AB=BC,PM⊥AD于点M,PN⊥CD于点N.
求证:
15.如图,在△ABC中,CD平分∠ACB,AE⊥CD,垂足为F,交BC于点E,若∠BAE=33°,∠B=37°,求∠EAC的度数.
16.如图,直线AE、CE分别被直线EF、AC所截,已知∠1=∠2,AB平分∠EAC,
CD平分∠ACG,将下列证明AB//CD的过程及理由填写完整.
证明:因为∠1=∠2,
所以 // ( ),
所以∠EAC=∠ACG( ),
因为AB平分∠EAC,CD平分∠ACG,
所以 = , = ,
所以 = ,
所以AB//CD( ).
17.如图,中,,为斜边边上的高,的角平分线分别交、于点E、F.过F作于G,试确定线段和的关系,并说明理由.
18.如图,在 中, 点 在 上,过点 作 于点 点 是 边上一点,连接 .若 ,求证: 平分 .
参考答案:
1.D
2.B
3.C
4.A
5.C
6.C
7.C
8.A
9.50°
10.12
11.4
12.
13.
14.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∴BD平分∠ADC,
∵PM⊥AD,PN⊥CD,
∴PM=PN.
15.解:∵AE⊥CD交CD于点F,
∴∠AFC=∠EFC=90°,
∵CD平分∠ACB,
∴∠ACF=∠ECF,
∵∠AFC+∠CAF+∠ACF=180°,∠EFC+∠CEA+∠ECF=180°,
∴∠CAF=∠CEA,
∵∠CEA=∠B+∠BAE,∠B=37°,∠BAE=33°,
∴∠EAC=∠CEA=70°,
∴∠EAC的度数为70°.
16.解:AE;FG;同位角相等,两直线平行;两直线平行,内错角相等;∠3;∠4;∠3;∠4;内错角相等,两直线平行
17.解:,,理由如下:
∵平分,,,
∴,,
∴在和中,,,
∴≌(HL),
∴,
∵,
∴,
∴,
∴,
又∵,
∴.
又∵,
∴,
∴.
又∵,
∴,
即,.
18.证明:由题意可得,在 和 中,
,
平分 .
一、单选题
1.如图, 平分 交 于点D, 于点E, 于点F.若 , , ,则 的长是( )
A.8 B.7 C.6 D.5
2.如图,点P是∠AOC的角平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最小值为( )
A.2 B.3 C.4 D.5
3.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于D.若BC=32,且CD∶BD=7∶9,则点D到边AB的距离为( )
A.7 B.9 C.14 D.18
4.如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是( )
A.在一个角的内部,且到角两边的距离相等的点在这个角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.测量垂直平分线上的点到这条线段的距离相等
5.如图,在△ABC中,∠C=90°,AC>BC.用直尺和圆规在边AC上确定一点P,使点P到AB、BC的距离相等,则符合要求的作图痕迹( )
A. B.
C. D.
6.用两把完全相同的长方形直尺按如图方式摆放,一把直尺压住射线OB交射线OA于点M,另一把直尺压住射线OA交第一把直尺于点P,作射线OP.若∠BOP=28°,则∠AMP的大小为( )
A.46° B.52° C.56° D.62°
7.如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=10,DE=3,则△BCE的面积为( )
A.30 B.16 C.15 D.13
8.如图,已知∠AOB,以点O为圆心,任意长度为半径画弧①,分别交OA,OB于点E,F,再以点E为圆心,EF的长为半径画弧,交弧①于点D,画射线OD.若∠AOB=26°,则∠BOD的度数为( )
A.52° B.38° C.28° D.54°
二、填空题
9.如图,在△ABC中,AC=BC,∠A=40 ,观察图中尺规作图的痕迹,可知∠BCG的度数为
10.如图,在△ABC中,∠A=90°,∠ABC=60°,以顶点B为圆心,适当长为半径画弧,分别交边AB、BC于点E、F;再分别以E、F为圆心,以大于长为半径画弧,两弧交于点P,作射线BP,交AC边于点G.若△ABG的面积是,则△BCG的面积为 .
11.如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是 .
12.如图,直线、相交于点O,平分,平分.若的度数为.则 .(用含α的代数式表示)
13.如图,在中,,分别是和的角平分线,过点作于点已知,的周长为,则的面积为 .
三、解答题
14.如图所示,已知BD为∠ABC的平分线,AB=BC,PM⊥AD于点M,PN⊥CD于点N.
求证:
15.如图,在△ABC中,CD平分∠ACB,AE⊥CD,垂足为F,交BC于点E,若∠BAE=33°,∠B=37°,求∠EAC的度数.
16.如图,直线AE、CE分别被直线EF、AC所截,已知∠1=∠2,AB平分∠EAC,
CD平分∠ACG,将下列证明AB//CD的过程及理由填写完整.
证明:因为∠1=∠2,
所以 // ( ),
所以∠EAC=∠ACG( ),
因为AB平分∠EAC,CD平分∠ACG,
所以 = , = ,
所以 = ,
所以AB//CD( ).
17.如图,中,,为斜边边上的高,的角平分线分别交、于点E、F.过F作于G,试确定线段和的关系,并说明理由.
18.如图,在 中, 点 在 上,过点 作 于点 点 是 边上一点,连接 .若 ,求证: 平分 .
参考答案:
1.D
2.B
3.C
4.A
5.C
6.C
7.C
8.A
9.50°
10.12
11.4
12.
13.
14.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∴BD平分∠ADC,
∵PM⊥AD,PN⊥CD,
∴PM=PN.
15.解:∵AE⊥CD交CD于点F,
∴∠AFC=∠EFC=90°,
∵CD平分∠ACB,
∴∠ACF=∠ECF,
∵∠AFC+∠CAF+∠ACF=180°,∠EFC+∠CEA+∠ECF=180°,
∴∠CAF=∠CEA,
∵∠CEA=∠B+∠BAE,∠B=37°,∠BAE=33°,
∴∠EAC=∠CEA=70°,
∴∠EAC的度数为70°.
16.解:AE;FG;同位角相等,两直线平行;两直线平行,内错角相等;∠3;∠4;∠3;∠4;内错角相等,两直线平行
17.解:,,理由如下:
∵平分,,,
∴,,
∴在和中,,,
∴≌(HL),
∴,
∵,
∴,
∴,
∴,
又∵,
∴.
又∵,
∴,
∴.
又∵,
∴,
即,.
18.证明:由题意可得,在 和 中,
,
平分 .
