2023-2024学年人教版九年级数学上册 24.4 扇形与圆锥专项练习 学案 (无答案)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册 24.4 扇形与圆锥专项练习 学案 (无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 175.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 20:32:21 | ||
图片预览

文档简介
扇形与圆锥专项练习
弧长与扇形面积
⊙O的半径为R,弧长为l,圆心角为n°,扇形的面积为S扇,则有如下公式:
(1) 弧长公式: 。
(2)扇形的面积公式: 。
圆柱和圆锥
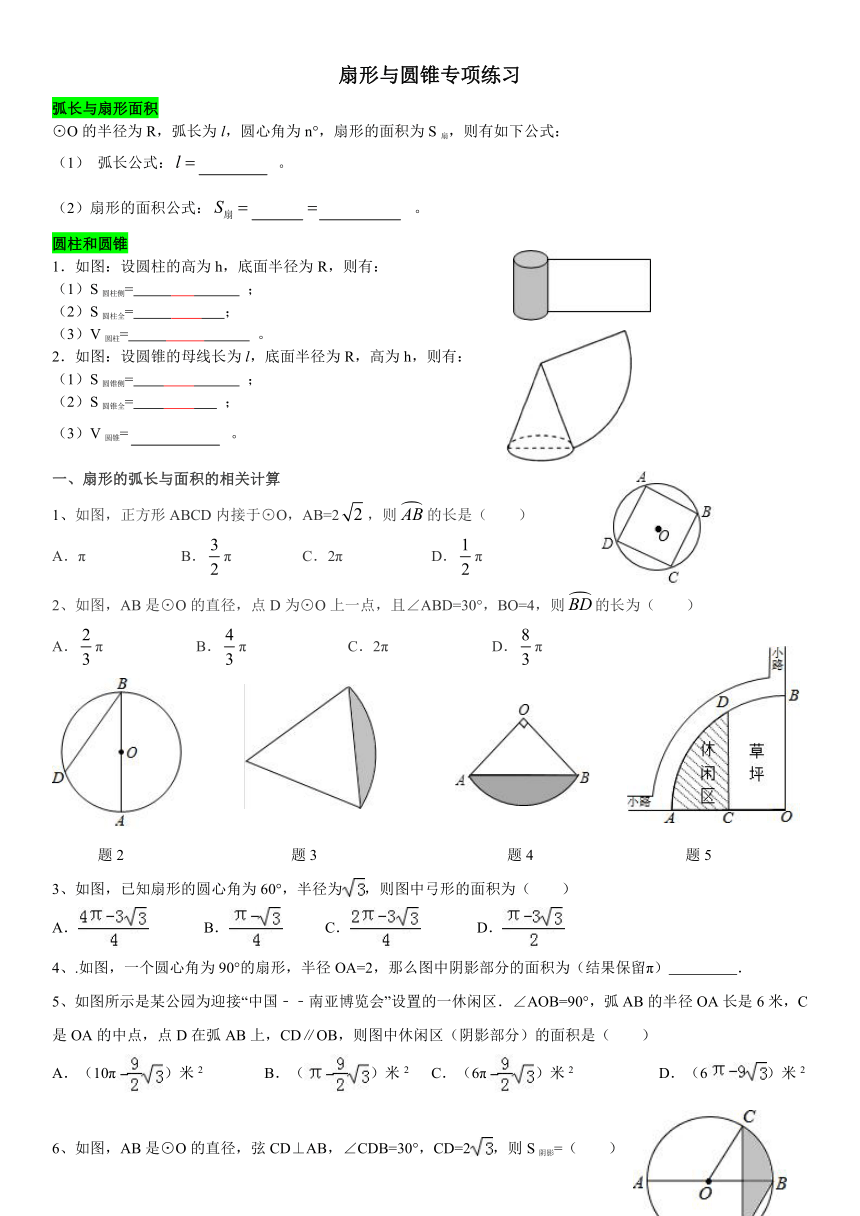
1.如图:设圆柱的高为h,底面半径为R,则有:
(1)S圆柱侧= ;
(2)S圆柱全= ;
(3)V圆柱= 。
2.如图:设圆锥的母线长为l,底面半径为R,高为h,则有:
(1)S圆锥侧= ;
(2)S圆锥全= ;
(3)V圆锥= 。
一、扇形的弧长与面积的相关计算
1、如图,正方形ABCD内接于⊙O,AB=2,则的长是( )
A.π B.π C.2π D.π
2、如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则的长为( )
A.π B.π C.2π D.π
题2 题3 题4 题5
3、如图,已知扇形的圆心角为60°,半径为,则图中弓形的面积为( )
A. B. C. D.
4、.如图,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为(结果保留π) .
5、如图所示是某公园为迎接“中国﹣﹣南亚博览会”设置的一休闲区.∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
A.(10π)米2 B.()米2 C.(6π)米2 D.(6)米2
6、如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则S阴影=( )
A.π B.2π C. D.π
题7 题8 题9 题10
7、.如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( )
A. B. C. D.
8、如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕A逆时针方向旋转40°得到△ADE,点B经过的路径为弧BD,是图中阴影部分的面积为( )
A.π-6 B.π C.π-3 D.+π
9、如图,半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )
A.(﹣1)cm2 B.(+1)cm2 C.1cm2 D.cm2
10.如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
A.18+36π B.24+18π C.18+18π D.12+18π
1.一个圆锥的母线长是9,底面圆的半径是6,则这个圆锥的侧面积是( )
A.81π B.27π C.54π D.18π
2.用一圆心角为120°,半径为6cm的扇形做成一个圆锥的侧面,这个圆锥的底面的半径是( )
A.1cm B.2cm C.3cm D.4cm
3.在学校组织的实践活动中,小新同学用纸板制作了一个圆锥模型,它的底面半径为1,高为2,则这个圆锥的侧面积是( )
A.4π B.3π C.2π D.2π
4.用如图所示的扇形纸片制作一个圆锥的侧面,要求圆锥的高是4cm,
底面周长是6πcm,则扇形的半径为( )
A.3cm B.5cm C.6cm D.8cm
5. 如图,蒙古包可近似地看作由圆锥和圆柱组成,若用毛毡搭建一个底面圆面积为25πm2,圆柱高为3m,圆锥高为2m的蒙古包,则需要毛毡的面积是( )
A.(30+5)π m2 B.40π m2 C.(30+5)π m2 D.55π m2
6.如图,在一张正方形纸片上剪下一个半径为r的圆形和一个半径为R的扇形,使之恰好围成图中所示的圆锥,则R与r之间的关系是 .
如图,圆锥的表面展开图由一扇形和一个圆组成,已知圆的面积为100π,扇形的圆心角为120°,这个扇形的面积为 .
如图,用一个半径为20cm,面积为150πcm2的扇形铁皮,制作一个无底的圆锥(不计接头损耗),则圆锥的底面半径r为 cm.
9.一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图扇形的圆心角是 .
10.如图,从直径为4cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是 cm.
弧长与扇形面积
⊙O的半径为R,弧长为l,圆心角为n°,扇形的面积为S扇,则有如下公式:
(1) 弧长公式: 。
(2)扇形的面积公式: 。
圆柱和圆锥
1.如图:设圆柱的高为h,底面半径为R,则有:
(1)S圆柱侧= ;
(2)S圆柱全= ;
(3)V圆柱= 。
2.如图:设圆锥的母线长为l,底面半径为R,高为h,则有:
(1)S圆锥侧= ;
(2)S圆锥全= ;
(3)V圆锥= 。
一、扇形的弧长与面积的相关计算
1、如图,正方形ABCD内接于⊙O,AB=2,则的长是( )
A.π B.π C.2π D.π
2、如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则的长为( )
A.π B.π C.2π D.π
题2 题3 题4 题5
3、如图,已知扇形的圆心角为60°,半径为,则图中弓形的面积为( )
A. B. C. D.
4、.如图,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为(结果保留π) .
5、如图所示是某公园为迎接“中国﹣﹣南亚博览会”设置的一休闲区.∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
A.(10π)米2 B.()米2 C.(6π)米2 D.(6)米2
6、如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则S阴影=( )
A.π B.2π C. D.π
题7 题8 题9 题10
7、.如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( )
A. B. C. D.
8、如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕A逆时针方向旋转40°得到△ADE,点B经过的路径为弧BD,是图中阴影部分的面积为( )
A.π-6 B.π C.π-3 D.+π
9、如图,半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )
A.(﹣1)cm2 B.(+1)cm2 C.1cm2 D.cm2
10.如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
A.18+36π B.24+18π C.18+18π D.12+18π
1.一个圆锥的母线长是9,底面圆的半径是6,则这个圆锥的侧面积是( )
A.81π B.27π C.54π D.18π
2.用一圆心角为120°,半径为6cm的扇形做成一个圆锥的侧面,这个圆锥的底面的半径是( )
A.1cm B.2cm C.3cm D.4cm
3.在学校组织的实践活动中,小新同学用纸板制作了一个圆锥模型,它的底面半径为1,高为2,则这个圆锥的侧面积是( )
A.4π B.3π C.2π D.2π
4.用如图所示的扇形纸片制作一个圆锥的侧面,要求圆锥的高是4cm,
底面周长是6πcm,则扇形的半径为( )
A.3cm B.5cm C.6cm D.8cm
5. 如图,蒙古包可近似地看作由圆锥和圆柱组成,若用毛毡搭建一个底面圆面积为25πm2,圆柱高为3m,圆锥高为2m的蒙古包,则需要毛毡的面积是( )
A.(30+5)π m2 B.40π m2 C.(30+5)π m2 D.55π m2
6.如图,在一张正方形纸片上剪下一个半径为r的圆形和一个半径为R的扇形,使之恰好围成图中所示的圆锥,则R与r之间的关系是 .
如图,圆锥的表面展开图由一扇形和一个圆组成,已知圆的面积为100π,扇形的圆心角为120°,这个扇形的面积为 .
如图,用一个半径为20cm,面积为150πcm2的扇形铁皮,制作一个无底的圆锥(不计接头损耗),则圆锥的底面半径r为 cm.
9.一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图扇形的圆心角是 .
10.如图,从直径为4cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是 cm.
同课章节目录
