2023-2024学年人教版九年级数学上册 第二十四章 圆测试题(含答案)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册 第二十四章 圆测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 204.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 21:01:42 | ||
图片预览


文档简介
第二十四章 圆测试题
一、选择题(每小题3分,共30分)
1.下列命题中正确的有( )
①弦是圆上任意两点之间的部分;②半径是弦;③直径是最长的弦;④弧是半圆,半圆是弧.
A.1个 B.2个 C.3个 D.4个
2.如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B,C点,则BC=( )
A.6 B.6 C.3 D.3
(
第
2
题图
) (
第
3
题图
) (
第
4
题图
) (
第
5
题图
)
3.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不一定成立的是( )
A.CM=DM B.= C.∠ACD=∠ADC D.OM=MB
4.如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为( )
A.60° B.70° C.80° D.90°
5.如图,一把直尺,60°的直角三角板和光盘如图摆放,A为60°角与直尺交点,AB=3,则光盘的直径是( )
A.3 B.3 C.6 D.6
(
A
B
P
O
C
)
(
第
10
题图
) (
第
9
题图
) (
第
8
题图
) (
第
6
题图
)
(
第
7
题图
)
6.已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC等于
A.10° B.20° C.30° D.40°
7.如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC等于( )
A.100° B.112.5° C.120° D.135°
8.)如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A. B.2 C.2 D.8
9.如图,⊙O是正五边形ABCDE的外接圆,点P是上的一点,则∠CPD的度数是( )
A.30° B.36° C.45° D.72°
10.如图,△ABC内接于⊙O,AB是⊙O的直径,AB=10,AC=BC,点E,F分别是边AC,BC的中点,点P是线段EF上的一个动点,连接AP,OP,则△AOP的周长的最小值为( )
A.5+10 B.5+5 C.10 D.15
二、填空题(每小题3分,共18分)
11.如图,点A、B、C、D在⊙O上,OB⊥AC,若∠BOC=56°,则∠ADB= 度.
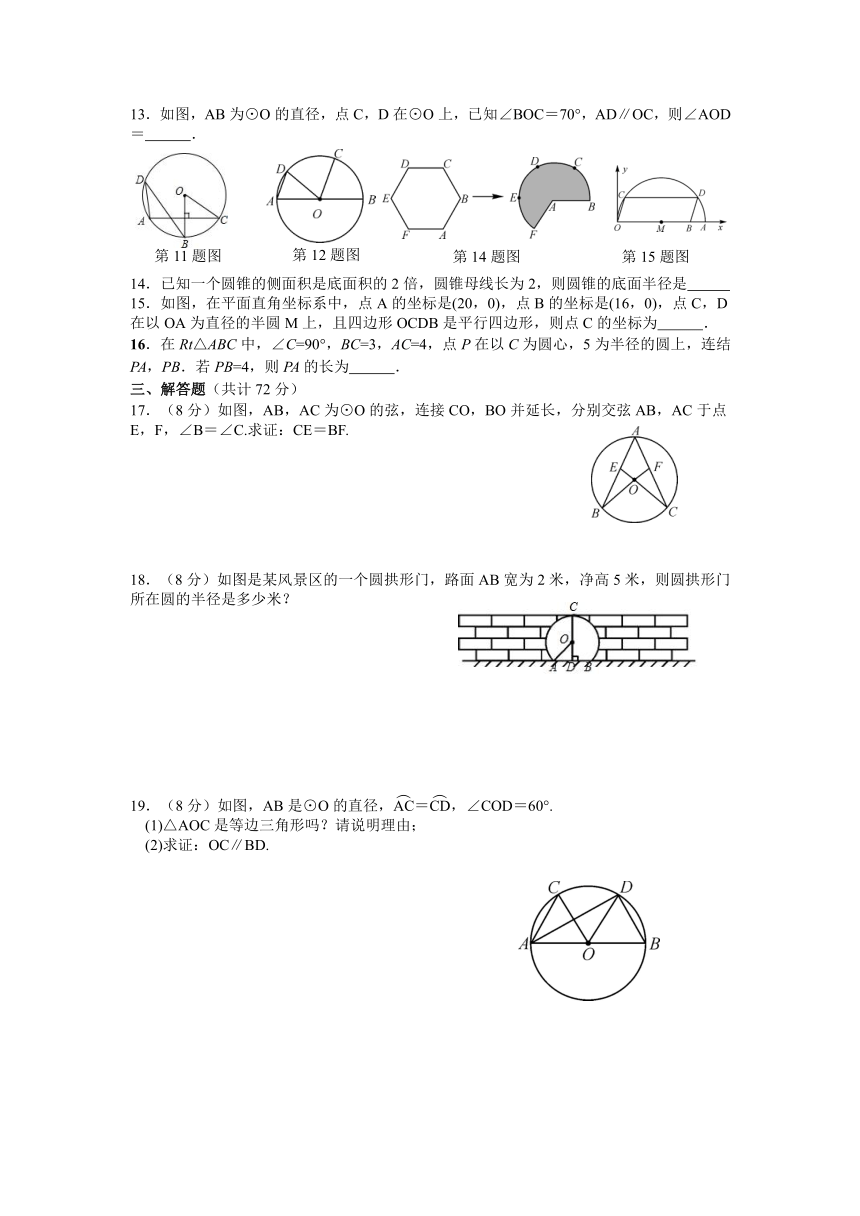
12.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形AFB(阴影部分)的面积为 .
13.如图,AB为⊙O的直径,点C,D在⊙O上,已知∠BOC=70°,AD∥OC,则∠AOD= .
(
第
15
题图
) (
第
14
题图
) (
第
12
题图
) (
第
11
题图
)
14.已知一个圆锥的侧面积是底面积的2倍,圆锥母线长为2,则圆锥的底面半径是
15.如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为 .
16.在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以C为圆心,5为半径的圆上,连结PA,PB.若PB=4,则PA的长为 .
三、解答题(共计72分)
17.(8分)如图,AB,AC为⊙O的弦,连接CO,BO并延长,分别交弦AB,AC于点E,F,∠B=∠C.求证:CE=BF.
18.(8分)如图是某风景区的一个圆拱形门,路面AB宽为2米,净高5米,则圆拱形门所在圆的半径是多少米?
19.(8分)如图,AB是⊙O的直径,=,∠COD=60°.
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC∥BD.
20.(8分))如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.
(1)求BC的长;
(2)求BD的长.
21.(8分)如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=,求⊙O的直径.
\
22.(10分)如图,⊙O为△ABC的外接圆,BC为直径,AD平分∠BAC交⊙O于点D,点M为△ABC的内心.
(1)求证:BC=DM;
(2)若DM=5,AB=8,求OM的长.
(
A
B
C
D
E
F
O
)23.(10分)如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF切⊙O于点E,交AD于点F,连接BE.
(1)求△CDF的面积;
(2)求线段BE的长.
24.(12分)如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.
第二十四章 圆参考答案
一、选择题
1.A 2.A 3.D 4.D 5.D 6.B 7.B 8.C 9.B 10.B
二、填空题
11.28 12.18 13.40
14.1 15(2,6) 16.3或
三、解答题:
17.证明:∵OB,OC是⊙O的半径,
∴OB=OC.
又∵∠B=∠C,∠BOE=∠COF,
∴△EOB≌△FOC(ASA).
∴OE=OF.
∴OE+OC=OF+OB,即CE=BF.
18.解:连接OA.
∵CD⊥AB,且CD过圆心O,
∴AD=AB=1米,∠CDA=90°.
设⊙O的半径为R,则
OA=OC=R,OD=5-R.
在Rt△OAD中,由勾股定理,得
OA2=OD2+AD2,即
R2=(5-R)2+12,解得R=2.6.
故圆拱形门所在圆的半径为2.6米.
19.解:(1)△AOC是等边三角形.
理由:∵=,
∴∠AOC=∠COD=60°.
又∵OA=OC,
∴△AOC是等边三角形.
(2)证明:∵∠AOC=∠COD=60°,
∴∠BOD=180°-(∠AOC+∠COD)=60°.
∵OD=OB,∴△ODB为等边三角形.
∴∠ODB=60°.
∴∠ODB=∠COD=60°.
∴OC∥BD.
20.解:(1)∵AB为⊙O的直径,
∴∠ACB=∠ADB=90°.
∴在Rt△ABC中,
BC===5.
(2)∵CD平分∠ACB,
∴∠ACD=∠BCD=45°.
∴∠BAD=∠ABD=45°.
∴AD=BD.
设BD=AD=x,在Rt△ABD中,由勾股定理,得AD2+BD2=AB2.
∴x2+x2=102.解得x=5.
∴BD=5.
21.解:(1)证明:连接OA,
∵∠B=60°,
∴∠AOC=2∠B=120°.
又∵OA=OC,
∴∠OAC=∠OCA=30°.
又∵AP=AC,∴∠P=∠ACP=30°.
∴∠OAP=∠AOC-∠P=90°.
∴OA⊥PA.
又∵OA为⊙O的半径,
∴PA是⊙O的切线.
(2)在Rt△OAP中,∵∠P=30°,
∴PO=2OA=OD+PD.
又∵OA=OD,∴PD=OA.
∵PD=,∴2OA=2PD=2.
∴⊙O的直径为2.
22.解:(1)证明:连接MC,DB,DC.
∵点M为△ABC的内心,
∴MC平分∠ACB.
∴∠ACM=∠BCM.
∵BC为直径,
∴∠BAC=90°.
∵AD平分∠BAC,
∴∠BAD=∠CAD=∠BAC=45°.
∴∠DBC=∠BCD=45°.
∴△BDC为等腰直角三角形.
∴BC=DC.
又∵∠DMC=∠MAC+∠ACM=45°+∠ACM,
而∠DCM=∠BCD+∠BCM,
∴∠DMC=∠DCM.
∴DC=DM.
∴BC=DM.
(2)作MF⊥BC于点F,ME⊥AC于点E,MH⊥AB于点H,连接OM.
∵DM=5,
∴BC=DM=10.
而AB=8,
∴AC==6.
设△ABC的内切圆半径为r,
∵点M为△ABC的内心,
∴MH=ME=MF=r.
∴四边形AHME为正方形.
∴AH=AE=r,则CE=CF=6-r,BH=BF=8-r.
而BF+FC=BC,
∴8-r+6-r=10,∴r=2.
∴MF=2,CF=6-2=4,
∵OC=5,
∴OF=5-4=1.
在Rt△OMF中,OM==.
23.(1)依题意可知:DA,CB,CF为⊙O的切线,∴AF=EF,CE=CB.设AF=x,则在Rt△FDC中,,∴.
∴S△FDC=.
(2)连接OC交BE于点G,连接OE.
∵CE,CB是⊙O的切线,∴CE=CB.
又∵OE=OB,∴CO垂直平分BE.
在Rt△OBC中,.
∵S△BOC=,∴BG=,
∴BE=2BG=.
24.(1)PN与⊙O相切.
证明:连接ON,则∠ONA=∠OAN,
∵PM=PN,∴∠PNM=∠PMN.
∵∠AMO=∠PMN,∴∠PNM=∠AMO.
∴∠PNO=∠PNM+∠ONA=∠AMO+∠ONA=90°.
即PN与⊙O相切.
(2)成立.
证明:连接ON,
则∠ONA=∠OAN,
∵PM=PN,∴∠PNM=∠PMN.
在Rt△AOM中,
∴∠OMA+∠OAM=90°,
∴∠PNM+∠ONA=90°.
∴∠PNO=180°﹣90°=90°.
即PN与⊙O相切.
(3)解:连接ON,由(2)可知∠ONP=90°.
∵∠AMO=15°,PM=PN,∴∠PNM=15°,∠OPN=30°,
∵∠PON=60°,∠AON=30°.
作NE⊥OD,垂足为点E,
则在△OEN中可求得:NE=.
S阴影=S△AOC+S扇形AON﹣S△CON=OC OA+CO NE
=×1×1+π﹣×1×
=π﹣.
一、选择题(每小题3分,共30分)
1.下列命题中正确的有( )
①弦是圆上任意两点之间的部分;②半径是弦;③直径是最长的弦;④弧是半圆,半圆是弧.
A.1个 B.2个 C.3个 D.4个
2.如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B,C点,则BC=( )
A.6 B.6 C.3 D.3
(
第
2
题图
) (
第
3
题图
) (
第
4
题图
) (
第
5
题图
)
3.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不一定成立的是( )
A.CM=DM B.= C.∠ACD=∠ADC D.OM=MB
4.如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为( )
A.60° B.70° C.80° D.90°
5.如图,一把直尺,60°的直角三角板和光盘如图摆放,A为60°角与直尺交点,AB=3,则光盘的直径是( )
A.3 B.3 C.6 D.6
(
A
B
P
O
C
)
(
第
10
题图
) (
第
9
题图
) (
第
8
题图
) (
第
6
题图
)
(
第
7
题图
)
6.已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC等于
A.10° B.20° C.30° D.40°
7.如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC等于( )
A.100° B.112.5° C.120° D.135°
8.)如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A. B.2 C.2 D.8
9.如图,⊙O是正五边形ABCDE的外接圆,点P是上的一点,则∠CPD的度数是( )
A.30° B.36° C.45° D.72°
10.如图,△ABC内接于⊙O,AB是⊙O的直径,AB=10,AC=BC,点E,F分别是边AC,BC的中点,点P是线段EF上的一个动点,连接AP,OP,则△AOP的周长的最小值为( )
A.5+10 B.5+5 C.10 D.15
二、填空题(每小题3分,共18分)
11.如图,点A、B、C、D在⊙O上,OB⊥AC,若∠BOC=56°,则∠ADB= 度.
12.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形AFB(阴影部分)的面积为 .
13.如图,AB为⊙O的直径,点C,D在⊙O上,已知∠BOC=70°,AD∥OC,则∠AOD= .
(
第
15
题图
) (
第
14
题图
) (
第
12
题图
) (
第
11
题图
)
14.已知一个圆锥的侧面积是底面积的2倍,圆锥母线长为2,则圆锥的底面半径是
15.如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为 .
16.在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以C为圆心,5为半径的圆上,连结PA,PB.若PB=4,则PA的长为 .
三、解答题(共计72分)
17.(8分)如图,AB,AC为⊙O的弦,连接CO,BO并延长,分别交弦AB,AC于点E,F,∠B=∠C.求证:CE=BF.
18.(8分)如图是某风景区的一个圆拱形门,路面AB宽为2米,净高5米,则圆拱形门所在圆的半径是多少米?
19.(8分)如图,AB是⊙O的直径,=,∠COD=60°.
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC∥BD.
20.(8分))如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.
(1)求BC的长;
(2)求BD的长.
21.(8分)如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=,求⊙O的直径.
\
22.(10分)如图,⊙O为△ABC的外接圆,BC为直径,AD平分∠BAC交⊙O于点D,点M为△ABC的内心.
(1)求证:BC=DM;
(2)若DM=5,AB=8,求OM的长.
(
A
B
C
D
E
F
O
)23.(10分)如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF切⊙O于点E,交AD于点F,连接BE.
(1)求△CDF的面积;
(2)求线段BE的长.
24.(12分)如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.
第二十四章 圆参考答案
一、选择题
1.A 2.A 3.D 4.D 5.D 6.B 7.B 8.C 9.B 10.B
二、填空题
11.28 12.18 13.40
14.1 15(2,6) 16.3或
三、解答题:
17.证明:∵OB,OC是⊙O的半径,
∴OB=OC.
又∵∠B=∠C,∠BOE=∠COF,
∴△EOB≌△FOC(ASA).
∴OE=OF.
∴OE+OC=OF+OB,即CE=BF.
18.解:连接OA.
∵CD⊥AB,且CD过圆心O,
∴AD=AB=1米,∠CDA=90°.
设⊙O的半径为R,则
OA=OC=R,OD=5-R.
在Rt△OAD中,由勾股定理,得
OA2=OD2+AD2,即
R2=(5-R)2+12,解得R=2.6.
故圆拱形门所在圆的半径为2.6米.
19.解:(1)△AOC是等边三角形.
理由:∵=,
∴∠AOC=∠COD=60°.
又∵OA=OC,
∴△AOC是等边三角形.
(2)证明:∵∠AOC=∠COD=60°,
∴∠BOD=180°-(∠AOC+∠COD)=60°.
∵OD=OB,∴△ODB为等边三角形.
∴∠ODB=60°.
∴∠ODB=∠COD=60°.
∴OC∥BD.
20.解:(1)∵AB为⊙O的直径,
∴∠ACB=∠ADB=90°.
∴在Rt△ABC中,
BC===5.
(2)∵CD平分∠ACB,
∴∠ACD=∠BCD=45°.
∴∠BAD=∠ABD=45°.
∴AD=BD.
设BD=AD=x,在Rt△ABD中,由勾股定理,得AD2+BD2=AB2.
∴x2+x2=102.解得x=5.
∴BD=5.
21.解:(1)证明:连接OA,
∵∠B=60°,
∴∠AOC=2∠B=120°.
又∵OA=OC,
∴∠OAC=∠OCA=30°.
又∵AP=AC,∴∠P=∠ACP=30°.
∴∠OAP=∠AOC-∠P=90°.
∴OA⊥PA.
又∵OA为⊙O的半径,
∴PA是⊙O的切线.
(2)在Rt△OAP中,∵∠P=30°,
∴PO=2OA=OD+PD.
又∵OA=OD,∴PD=OA.
∵PD=,∴2OA=2PD=2.
∴⊙O的直径为2.
22.解:(1)证明:连接MC,DB,DC.
∵点M为△ABC的内心,
∴MC平分∠ACB.
∴∠ACM=∠BCM.
∵BC为直径,
∴∠BAC=90°.
∵AD平分∠BAC,
∴∠BAD=∠CAD=∠BAC=45°.
∴∠DBC=∠BCD=45°.
∴△BDC为等腰直角三角形.
∴BC=DC.
又∵∠DMC=∠MAC+∠ACM=45°+∠ACM,
而∠DCM=∠BCD+∠BCM,
∴∠DMC=∠DCM.
∴DC=DM.
∴BC=DM.
(2)作MF⊥BC于点F,ME⊥AC于点E,MH⊥AB于点H,连接OM.
∵DM=5,
∴BC=DM=10.
而AB=8,
∴AC==6.
设△ABC的内切圆半径为r,
∵点M为△ABC的内心,
∴MH=ME=MF=r.
∴四边形AHME为正方形.
∴AH=AE=r,则CE=CF=6-r,BH=BF=8-r.
而BF+FC=BC,
∴8-r+6-r=10,∴r=2.
∴MF=2,CF=6-2=4,
∵OC=5,
∴OF=5-4=1.
在Rt△OMF中,OM==.
23.(1)依题意可知:DA,CB,CF为⊙O的切线,∴AF=EF,CE=CB.设AF=x,则在Rt△FDC中,,∴.
∴S△FDC=.
(2)连接OC交BE于点G,连接OE.
∵CE,CB是⊙O的切线,∴CE=CB.
又∵OE=OB,∴CO垂直平分BE.
在Rt△OBC中,.
∵S△BOC=,∴BG=,
∴BE=2BG=.
24.(1)PN与⊙O相切.
证明:连接ON,则∠ONA=∠OAN,
∵PM=PN,∴∠PNM=∠PMN.
∵∠AMO=∠PMN,∴∠PNM=∠AMO.
∴∠PNO=∠PNM+∠ONA=∠AMO+∠ONA=90°.
即PN与⊙O相切.
(2)成立.
证明:连接ON,
则∠ONA=∠OAN,
∵PM=PN,∴∠PNM=∠PMN.
在Rt△AOM中,
∴∠OMA+∠OAM=90°,
∴∠PNM+∠ONA=90°.
∴∠PNO=180°﹣90°=90°.
即PN与⊙O相切.
(3)解:连接ON,由(2)可知∠ONP=90°.
∵∠AMO=15°,PM=PN,∴∠PNM=15°,∠OPN=30°,
∵∠PON=60°,∠AON=30°.
作NE⊥OD,垂足为点E,
则在△OEN中可求得:NE=.
S阴影=S△AOC+S扇形AON﹣S△CON=OC OA+CO NE
=×1×1+π﹣×1×
=π﹣.
同课章节目录
