安徽省蚌埠市固镇县2022-2023学年下学期七年级期末数学试卷(含解析)
文档属性
| 名称 | 安徽省蚌埠市固镇县2022-2023学年下学期七年级期末数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 59.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 00:00:00 | ||
图片预览



文档简介
2022-2023学年安徽省蚌埠市固镇县七年级(下)期末数学试卷
一、选择题(30分)
1. 在实数、、、、、……和3之间的2逐次加1个中,无理数的个数为( )
A. 2个 B. 3个 C. 4个 D. 5个
2. 如图,在数轴上表示实数的点可能是( )
A. P B. Q C. R D. S
3. 若是关于x的完全平方式,则m的值为( )
A. 7或 B. C. 7 D. 5或1
4. 下列运算正确的是( )
A. B. C. D.
5. 绿色植物靠吸收光量子来进行光合作用,已知每个光量子的波长约为688纳米,1纳米米,则每个光量子的波长可用科学记数法表示为米.( )
A. B. C. D.
6. 下列分式中,是最简分式的是( )
A. B. C. D.
7. 如图所示,共有3个方格块,现在要把上面的方格块与下面的两个方格块合成一个长方形的整体,则应将上面的方格块( )
A. 向右平移1格,向下3格
B. 向右平移1格,向下4格
C. 向右平移2格,向下3格
D. 向右平移2格,向下4格
8. 下列各式的因式分解正确的是( )
A. B.
C. D.
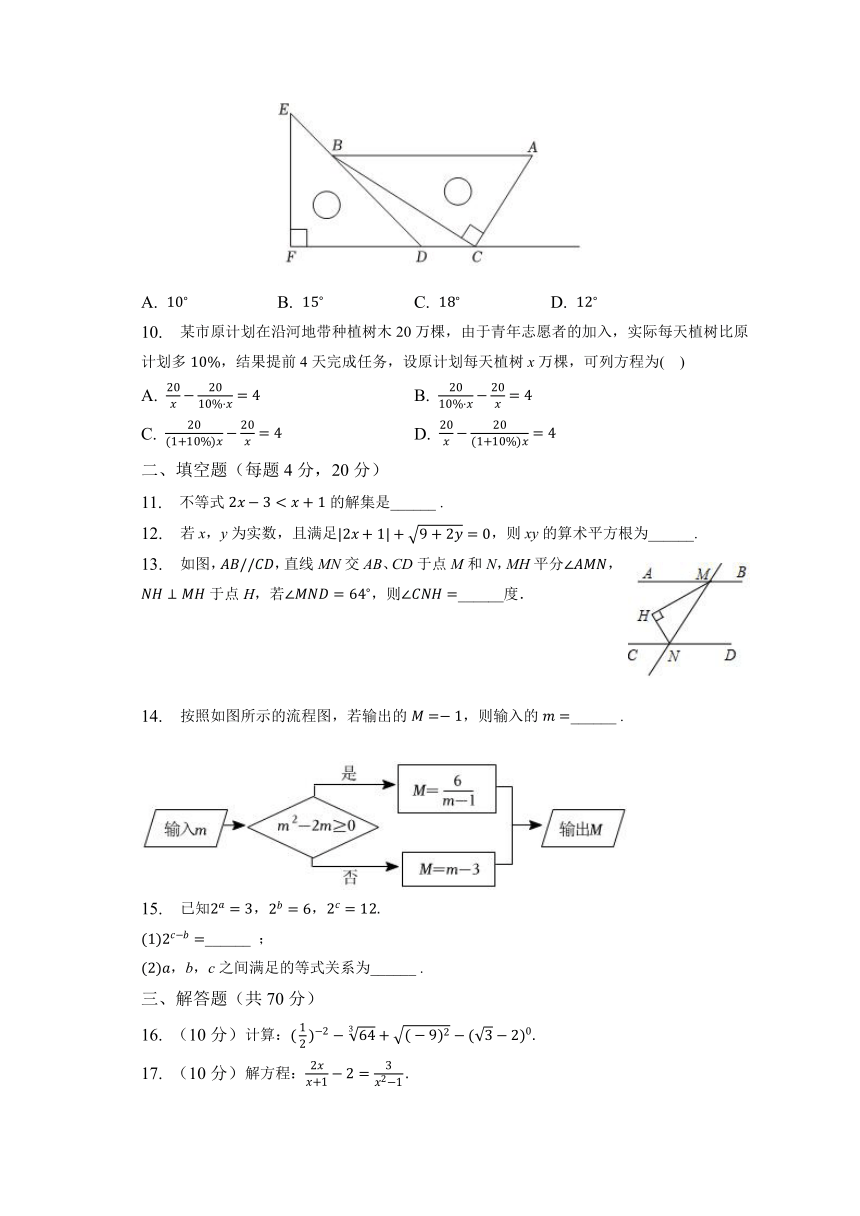
9. 一副直角三角板如图放置,点C在FD的延长线上,,,,,则的大小为( )
A. B. C. D.
10. 某市原计划在沿河地带种植树木20万棵,由于青年志愿者的加入,实际每天植树比原计划多,结果提前4天完成任务,设原计划每天植树x万棵,可列方程为( )
A. B.
C. D.
二、填空题(每题4分,20分)
11. 不等式的解集是______ .
12. 若x,y为实数,且满足,则xy的算术平方根为______.
13. 如图,,直线MN交AB、CD于点M和N,MH平分,于点H,若,则______度.
14. 按照如图所示的流程图,若输出的,则输入的______ .
15. 已知,,
______ ;
,b,c之间满足的等式关系为______ .
三、解答题(共70分)
16. (10分)计算:
17. (10分)解方程:
18. (12分)如图,已知,
请判断与是否相等,并说明理由;
若AC平分,于点E,,求的度数.
19. (12分)已知A,B为多项式,且,
若A与B的乘积中不含项和项,求m,n的值;
在数轴上,将表示数m的点记为M,表示数n的点记为在的条件下,数轴上的点P满足P到点M的距离是P到点N距离的2倍,求点P表示的数.
20. (12分)为了深入贯彻习总书记关于“双减”工作的重要指示,增强学生的体质,济南市某中学决定购买一些篮球和足球来促进学生的体育锻炼,已知每个篮球的售价比每个足球的售价单价多20元,并且花费6000元购买篮球的数量是花费3200元购买足球数量的倍.
求篮球和足球的单价分别是多少元?
根据学校的实际需求,需要一次性购买篮球和足球共200个,并且要求购买篮球和足球的总费用不超过9600元,那么学校最少购入多少个足球?
21.(14分)[阅读理解]
若x满足,求的值.
解:设,,
则,,
所以
[迁移运用]
请仿照上面的方法求解下面问题:
若x满足,求的值;
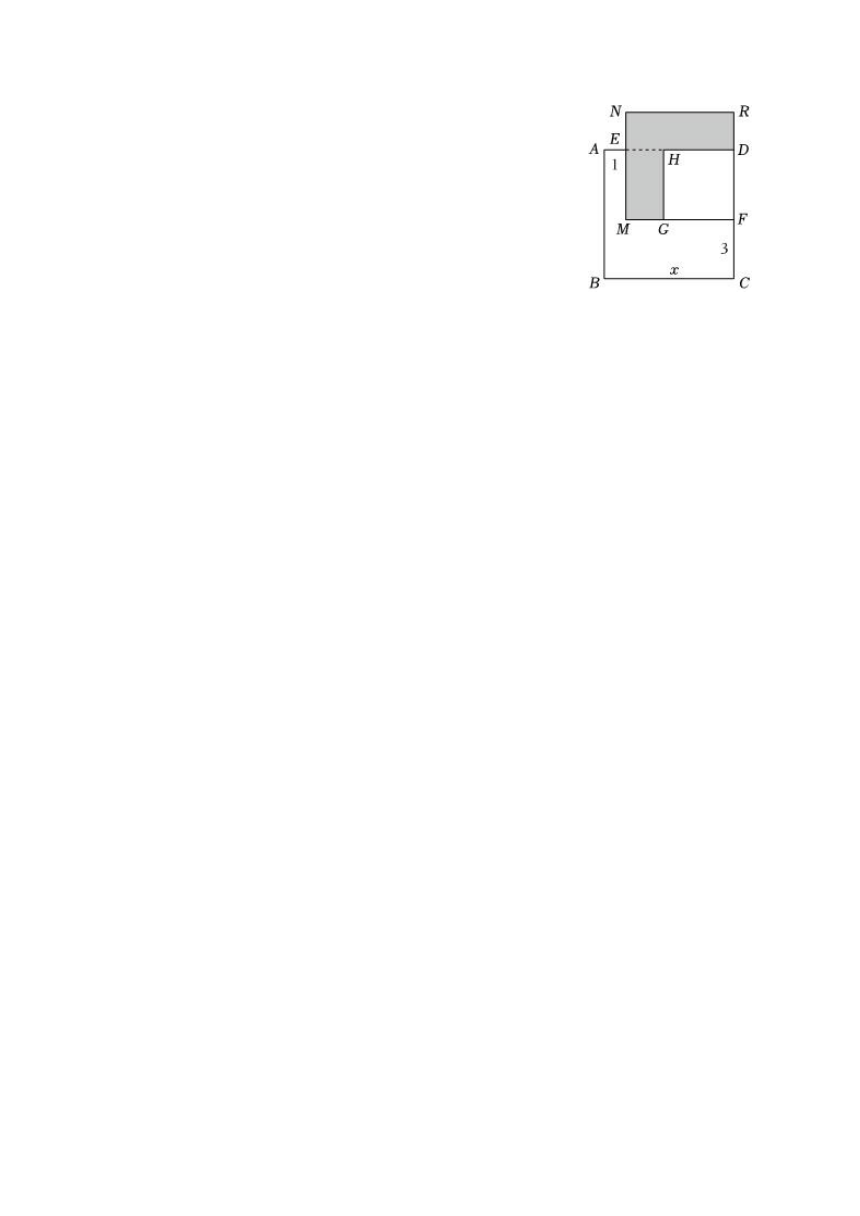
如图,已知正方形ABCD的边长为x,E,F分别是AD,DC上的点,且,,长方形EMFD的面积是48,分别以MF,DF为边作正方形MFRN和正方形GFDH,求阴影部分的面积.
答案和解析
1.【答案】C
【解析】解:,,,……和3之间的2逐次加1个是无理数,
有4个,
故选:
逐个数进行判断得出答案.
本题考查无理数的意义,掌握无限不循环的小数是无理数是正确判断的前提.
2.【答案】B
【解析】
【分析】
本题考查了实数与数轴,无理数的大小,确定出的范围是解题的关键.先判断出的范围,然后根据数轴判断即可.
【解答】
解:,
,
,
在数轴上表示实数的点可能是
故选:
3.【答案】A
【解析】
【分析】
此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.
利用完全平方公式的结构特征判断即可确定出m的值.
【解答】
解:是关于x的完全平方式,
,即,
解得或
故选:
4.【答案】D
【解析】
【分析】
本题主要考查幂的乘方、合并同类项、同底数幂的乘法及分式的乘方的运算.分别根据幂的乘方、合并同类项法则、同底数幂的乘法及分式的乘方逐一计算即可判断.
【解答】
解:A、,此选项错误;
B、,此选项错误;
C、,此选项错误;
D、,此选项正确.
故选
5.【答案】B
【解析】解:纳米米,
纳米米
故选:
绝对值小于1的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为,其中,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
6.【答案】C
【解析】解:A、该分式的分子和分母中含有公因数2,不是最简分式,故本选项不符合题意;
B、该分式的分子和分母中含有公因式a,不是最简分式,故本选项不符合题意;
C、该分式的分子和分母除1外没有其它的公因式,是最简分式,故本选项符合题意;
D、该分式的分子和分母中含有公因式,不是最简分式,故本选项不符合题意;
故选:
根据最简分式的定义分式的分子和分母除1以外没有其它的公因式,叫最简分式逐个判断即可.
本题考查了最简分式的定义,能熟记最简分式的定义是解此题的关键.
7.【答案】D
【解析】解:上面的图案的最右边需向右平移2格才能与下面图案的最右边在一条直线上,最下边需向下平移4格才能与下面图案的最下面重合,
故选:
找到两个图案的最右边移动到一条直线,最下边移动到一条直线上的距离即可.
此题考查的是平移的性质,解决本题的关键是得到两个图案重合需移动的左右距离和上下距离.
8.【答案】D
【解析】解:,因此选项A不符合题意;
B.,因此选项B不符合题意;
C.,因此选项C不符合题意;
D.,因此选项D符合题意;
故选:
根据提公因式法、完全平方公式、平方差公式以及十字相乘法将各个选项中的多项式进行因式分解即可.
本题考查提公因式法、公式法分解因式,掌握提公因式法、十字相乘法以及完全平方公式、平方差公式是正确解答的前提.
9.【答案】B
【解析】解:,
,
,,
,
,,
,
故选:
根据平行线的性质可知,再利用直角三角形的性质可知、即可解答.
本题考查了平行线的性质,直角三角形的性质,角的和差关系,掌握直角三角形的性质是解题的关键.
10.【答案】D
【解析】解:设原计划每天植树x万棵,则实际每天植树万棵,
根据题意得:
故选:
根据“提前4天完成任务”即可列出方程.
本题考查由实际问题抽象出分式方程,解题的关键是利用题目中的等量关系,本题属于基础题型.
11.【答案】
【解析】解:,
,
,
故答案为:
按照解一元一次不等式的步骤,进行计算即可解答.
本题考查了解一元一次不等式,熟练掌握解一元一次不等式的步骤是解题的关键.
12.【答案】
【解析】
【分析】
本题考查了偶次方和绝对值的非负性,算术平方根的应用,关键是求出x、y的值.
根据偶次方和绝对值的非负性得出方程,求出方程的解,再代入求出算术平方根即可.
【解答】
解:,
,,
,,
,
故答案为
13.【答案】58
【解析】
【分析】
本题考查的是平行线的性质以及垂线的定义,用到的知识点为:两直线平行,内错角相等.
依据平行线的性质,即可得到,再根据MH平分,,即可得出,进而得到
【解答】
解:,
,
平分,
,
又,
,
,
故答案为:
14.【答案】或2
【解析】解:当时,
,解得,
经检验,是原方程的解,并且满足;
当时,
,解得,满足
故答案为:或
根据题目中的程序,利用分类讨论的方法可以分别求得m的值,从而可以解答本题.
本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.
15.【答案】
【解析】解:当,,时,
,
故答案为:2;
,
,
,
,
,
故答案为:
利用同底数幂的除法的法则进行运算即可;
结合所给的条件进行整理即可求解.
本题主要考查幂的乘方,同底数幂的除法,解答的关键是对相应的运算法则的掌握.
16.【答案】解:原式
【解析】利用负整数指数幂,立方根的定义,算术平方根的定义,零指数幂进行计算即可.
本题考查实数的运算,熟练掌握相关运算法则是解题的关键.
17.【答案】解:,
,
解得:,
检验:当时,,
是原方程的根.
【解析】按照解分式方程的步骤,进行计算即可解答.
本题考查了解分式方程,一定要注意解分式方程必须检验,
18.【答案】解:,
理由如下:
因为,
所以,
又因为,
所以,
所以,
所以;
因为AC平分,
所以,,
由知,
所以,
所以,
因为,
所以,
因为,,
所以,
所以,
所以
【解析】由已知可证得,根据平行线的判定得到,根据平行线的性质即可得到;
根据角平分线的定义得到,即,由平行线的性质可求得,再由平行线的判定和性质定理求出,继而求出
本题考查了平行线的性质,角平分线的定义,根据平行线的性质和角平分线的定义求出是解题的关键.
19.【答案】解:
依题意,,,
解得,
设点P表示的数为a,由题意得:,
①若,解得;
②若,解得
所以,点P表示的数为12或
【解析】将展开合并后,根据不含项和项,则对应的系数为0,解出即可;
根据绝对值的几何意义列出代数式,分情况去绝对值求出点P表示的数即可.
本题考查了多项式乘多项式以及绝对值的几何意义,数轴上表示数a的点到原点的距离即
20.【答案】解:设每个足球的售价为x元,则每个篮球的售价为元,
由题意得:,
解得:,
经检验,是所列方程的解且符合题意,
,
答:每个足球的售价为40元,每个篮球的售价为60元;
设购入m个足球,则购入个篮球,
由题意得:,
解得:,
答:学校最少购入120个足球.
【解析】设每个足球的售价为x元,则每个篮球的售价为元.由题意:花费6000元购买篮球的数量是花费3200元购买足球数量的倍.列出分式方程,解方程即可;
设购入m个足球,则购入个篮球.由题意:购买篮球和足球的总费用不超过9600元,列出一元一次不等式,解不等式即可.
本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:找准等量关系,正确列出分式方程;根据各数量之间的关系,正确列出一元一次不等式.
21.【答案】解:设,,
,
,
,
,
,
的值为11;
正方形ABCD的边长为x,,,
,,
长方形EMFD的面积是48,
,
设,,
,,
,
或舍去,
阴影部分的面积=正方形MFRN的面积-正方形GFDH的面积,
阴影部分的面积是
【解析】利用例题的解题思路进行计算,即可解答;
根据已知易得,,从而可得,然后设,,则,,从而利用完全平方公式可得,进而可得,最后根据阴影部分的面积=正方形MFRN的面积-正方形GFDH的面积,再利用平方差公式进行计算,即可解答.
本题考查了整式的混合运算-化简求值,完全平方公式的几何背景,平方差公式,理解例题的解题思路是解题的关键.
一、选择题(30分)
1. 在实数、、、、、……和3之间的2逐次加1个中,无理数的个数为( )
A. 2个 B. 3个 C. 4个 D. 5个
2. 如图,在数轴上表示实数的点可能是( )
A. P B. Q C. R D. S
3. 若是关于x的完全平方式,则m的值为( )
A. 7或 B. C. 7 D. 5或1
4. 下列运算正确的是( )
A. B. C. D.
5. 绿色植物靠吸收光量子来进行光合作用,已知每个光量子的波长约为688纳米,1纳米米,则每个光量子的波长可用科学记数法表示为米.( )
A. B. C. D.
6. 下列分式中,是最简分式的是( )
A. B. C. D.
7. 如图所示,共有3个方格块,现在要把上面的方格块与下面的两个方格块合成一个长方形的整体,则应将上面的方格块( )
A. 向右平移1格,向下3格
B. 向右平移1格,向下4格
C. 向右平移2格,向下3格
D. 向右平移2格,向下4格
8. 下列各式的因式分解正确的是( )
A. B.
C. D.
9. 一副直角三角板如图放置,点C在FD的延长线上,,,,,则的大小为( )
A. B. C. D.
10. 某市原计划在沿河地带种植树木20万棵,由于青年志愿者的加入,实际每天植树比原计划多,结果提前4天完成任务,设原计划每天植树x万棵,可列方程为( )
A. B.
C. D.
二、填空题(每题4分,20分)
11. 不等式的解集是______ .
12. 若x,y为实数,且满足,则xy的算术平方根为______.
13. 如图,,直线MN交AB、CD于点M和N,MH平分,于点H,若,则______度.
14. 按照如图所示的流程图,若输出的,则输入的______ .
15. 已知,,
______ ;
,b,c之间满足的等式关系为______ .
三、解答题(共70分)
16. (10分)计算:
17. (10分)解方程:
18. (12分)如图,已知,
请判断与是否相等,并说明理由;
若AC平分,于点E,,求的度数.
19. (12分)已知A,B为多项式,且,
若A与B的乘积中不含项和项,求m,n的值;
在数轴上,将表示数m的点记为M,表示数n的点记为在的条件下,数轴上的点P满足P到点M的距离是P到点N距离的2倍,求点P表示的数.
20. (12分)为了深入贯彻习总书记关于“双减”工作的重要指示,增强学生的体质,济南市某中学决定购买一些篮球和足球来促进学生的体育锻炼,已知每个篮球的售价比每个足球的售价单价多20元,并且花费6000元购买篮球的数量是花费3200元购买足球数量的倍.
求篮球和足球的单价分别是多少元?
根据学校的实际需求,需要一次性购买篮球和足球共200个,并且要求购买篮球和足球的总费用不超过9600元,那么学校最少购入多少个足球?
21.(14分)[阅读理解]
若x满足,求的值.
解:设,,
则,,
所以
[迁移运用]
请仿照上面的方法求解下面问题:
若x满足,求的值;
如图,已知正方形ABCD的边长为x,E,F分别是AD,DC上的点,且,,长方形EMFD的面积是48,分别以MF,DF为边作正方形MFRN和正方形GFDH,求阴影部分的面积.
答案和解析
1.【答案】C
【解析】解:,,,……和3之间的2逐次加1个是无理数,
有4个,
故选:
逐个数进行判断得出答案.
本题考查无理数的意义,掌握无限不循环的小数是无理数是正确判断的前提.
2.【答案】B
【解析】
【分析】
本题考查了实数与数轴,无理数的大小,确定出的范围是解题的关键.先判断出的范围,然后根据数轴判断即可.
【解答】
解:,
,
,
在数轴上表示实数的点可能是
故选:
3.【答案】A
【解析】
【分析】
此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.
利用完全平方公式的结构特征判断即可确定出m的值.
【解答】
解:是关于x的完全平方式,
,即,
解得或
故选:
4.【答案】D
【解析】
【分析】
本题主要考查幂的乘方、合并同类项、同底数幂的乘法及分式的乘方的运算.分别根据幂的乘方、合并同类项法则、同底数幂的乘法及分式的乘方逐一计算即可判断.
【解答】
解:A、,此选项错误;
B、,此选项错误;
C、,此选项错误;
D、,此选项正确.
故选
5.【答案】B
【解析】解:纳米米,
纳米米
故选:
绝对值小于1的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为,其中,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
6.【答案】C
【解析】解:A、该分式的分子和分母中含有公因数2,不是最简分式,故本选项不符合题意;
B、该分式的分子和分母中含有公因式a,不是最简分式,故本选项不符合题意;
C、该分式的分子和分母除1外没有其它的公因式,是最简分式,故本选项符合题意;
D、该分式的分子和分母中含有公因式,不是最简分式,故本选项不符合题意;
故选:
根据最简分式的定义分式的分子和分母除1以外没有其它的公因式,叫最简分式逐个判断即可.
本题考查了最简分式的定义,能熟记最简分式的定义是解此题的关键.
7.【答案】D
【解析】解:上面的图案的最右边需向右平移2格才能与下面图案的最右边在一条直线上,最下边需向下平移4格才能与下面图案的最下面重合,
故选:
找到两个图案的最右边移动到一条直线,最下边移动到一条直线上的距离即可.
此题考查的是平移的性质,解决本题的关键是得到两个图案重合需移动的左右距离和上下距离.
8.【答案】D
【解析】解:,因此选项A不符合题意;
B.,因此选项B不符合题意;
C.,因此选项C不符合题意;
D.,因此选项D符合题意;
故选:
根据提公因式法、完全平方公式、平方差公式以及十字相乘法将各个选项中的多项式进行因式分解即可.
本题考查提公因式法、公式法分解因式,掌握提公因式法、十字相乘法以及完全平方公式、平方差公式是正确解答的前提.
9.【答案】B
【解析】解:,
,
,,
,
,,
,
故选:
根据平行线的性质可知,再利用直角三角形的性质可知、即可解答.
本题考查了平行线的性质,直角三角形的性质,角的和差关系,掌握直角三角形的性质是解题的关键.
10.【答案】D
【解析】解:设原计划每天植树x万棵,则实际每天植树万棵,
根据题意得:
故选:
根据“提前4天完成任务”即可列出方程.
本题考查由实际问题抽象出分式方程,解题的关键是利用题目中的等量关系,本题属于基础题型.
11.【答案】
【解析】解:,
,
,
故答案为:
按照解一元一次不等式的步骤,进行计算即可解答.
本题考查了解一元一次不等式,熟练掌握解一元一次不等式的步骤是解题的关键.
12.【答案】
【解析】
【分析】
本题考查了偶次方和绝对值的非负性,算术平方根的应用,关键是求出x、y的值.
根据偶次方和绝对值的非负性得出方程,求出方程的解,再代入求出算术平方根即可.
【解答】
解:,
,,
,,
,
故答案为
13.【答案】58
【解析】
【分析】
本题考查的是平行线的性质以及垂线的定义,用到的知识点为:两直线平行,内错角相等.
依据平行线的性质,即可得到,再根据MH平分,,即可得出,进而得到
【解答】
解:,
,
平分,
,
又,
,
,
故答案为:
14.【答案】或2
【解析】解:当时,
,解得,
经检验,是原方程的解,并且满足;
当时,
,解得,满足
故答案为:或
根据题目中的程序,利用分类讨论的方法可以分别求得m的值,从而可以解答本题.
本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.
15.【答案】
【解析】解:当,,时,
,
故答案为:2;
,
,
,
,
,
故答案为:
利用同底数幂的除法的法则进行运算即可;
结合所给的条件进行整理即可求解.
本题主要考查幂的乘方,同底数幂的除法,解答的关键是对相应的运算法则的掌握.
16.【答案】解:原式
【解析】利用负整数指数幂,立方根的定义,算术平方根的定义,零指数幂进行计算即可.
本题考查实数的运算,熟练掌握相关运算法则是解题的关键.
17.【答案】解:,
,
解得:,
检验:当时,,
是原方程的根.
【解析】按照解分式方程的步骤,进行计算即可解答.
本题考查了解分式方程,一定要注意解分式方程必须检验,
18.【答案】解:,
理由如下:
因为,
所以,
又因为,
所以,
所以,
所以;
因为AC平分,
所以,,
由知,
所以,
所以,
因为,
所以,
因为,,
所以,
所以,
所以
【解析】由已知可证得,根据平行线的判定得到,根据平行线的性质即可得到;
根据角平分线的定义得到,即,由平行线的性质可求得,再由平行线的判定和性质定理求出,继而求出
本题考查了平行线的性质,角平分线的定义,根据平行线的性质和角平分线的定义求出是解题的关键.
19.【答案】解:
依题意,,,
解得,
设点P表示的数为a,由题意得:,
①若,解得;
②若,解得
所以,点P表示的数为12或
【解析】将展开合并后,根据不含项和项,则对应的系数为0,解出即可;
根据绝对值的几何意义列出代数式,分情况去绝对值求出点P表示的数即可.
本题考查了多项式乘多项式以及绝对值的几何意义,数轴上表示数a的点到原点的距离即
20.【答案】解:设每个足球的售价为x元,则每个篮球的售价为元,
由题意得:,
解得:,
经检验,是所列方程的解且符合题意,
,
答:每个足球的售价为40元,每个篮球的售价为60元;
设购入m个足球,则购入个篮球,
由题意得:,
解得:,
答:学校最少购入120个足球.
【解析】设每个足球的售价为x元,则每个篮球的售价为元.由题意:花费6000元购买篮球的数量是花费3200元购买足球数量的倍.列出分式方程,解方程即可;
设购入m个足球,则购入个篮球.由题意:购买篮球和足球的总费用不超过9600元,列出一元一次不等式,解不等式即可.
本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:找准等量关系,正确列出分式方程;根据各数量之间的关系,正确列出一元一次不等式.
21.【答案】解:设,,
,
,
,
,
,
的值为11;
正方形ABCD的边长为x,,,
,,
长方形EMFD的面积是48,
,
设,,
,,
,
或舍去,
阴影部分的面积=正方形MFRN的面积-正方形GFDH的面积,
阴影部分的面积是
【解析】利用例题的解题思路进行计算,即可解答;
根据已知易得,,从而可得,然后设,,则,,从而利用完全平方公式可得,进而可得,最后根据阴影部分的面积=正方形MFRN的面积-正方形GFDH的面积,再利用平方差公式进行计算,即可解答.
本题考查了整式的混合运算-化简求值,完全平方公式的几何背景,平方差公式,理解例题的解题思路是解题的关键.
同课章节目录
