2023年中考数学专题:全等三角形辅助线(截长补短、倍长中线)(无答案)
文档属性
| 名称 | 2023年中考数学专题:全等三角形辅助线(截长补短、倍长中线)(无答案) | 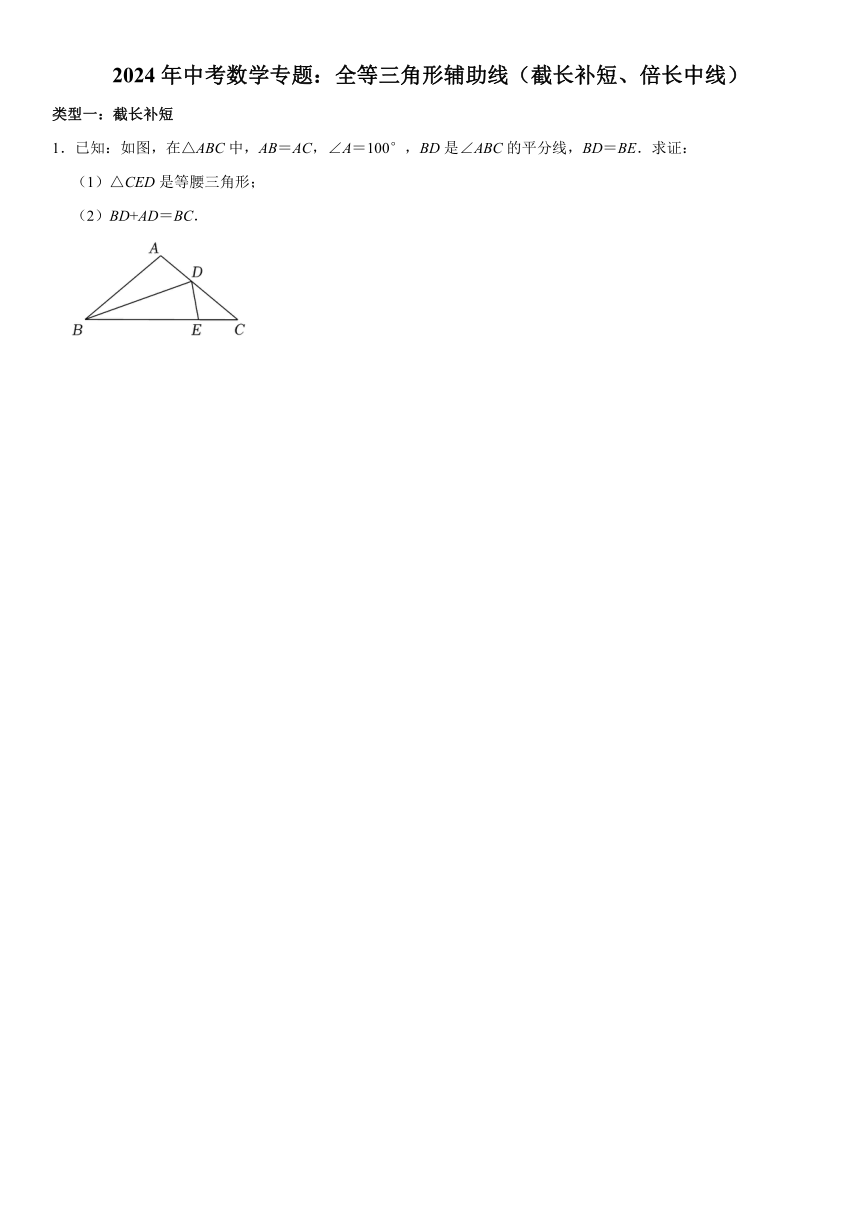 | |
| 格式 | docx | ||
| 文件大小 | 348.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 17:15:43 | ||
图片预览


文档简介
2024年中考数学专题:全等三角形辅助线(截长补短、倍长中线)
类型一:截长补短
1.已知:如图,在△ABC中,AB=AC,∠A=100°,BD是∠ABC的平分线,BD=BE.求证:
(1)△CED是等腰三角形;
(2)BD+AD=BC.
2.在Rt△ABC中,∠ABC=90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE.AC=DE,BC=BE.
(1)求证:AB=BD;
(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG.当KB平分∠AKG时,求证:AK=DG+KG.
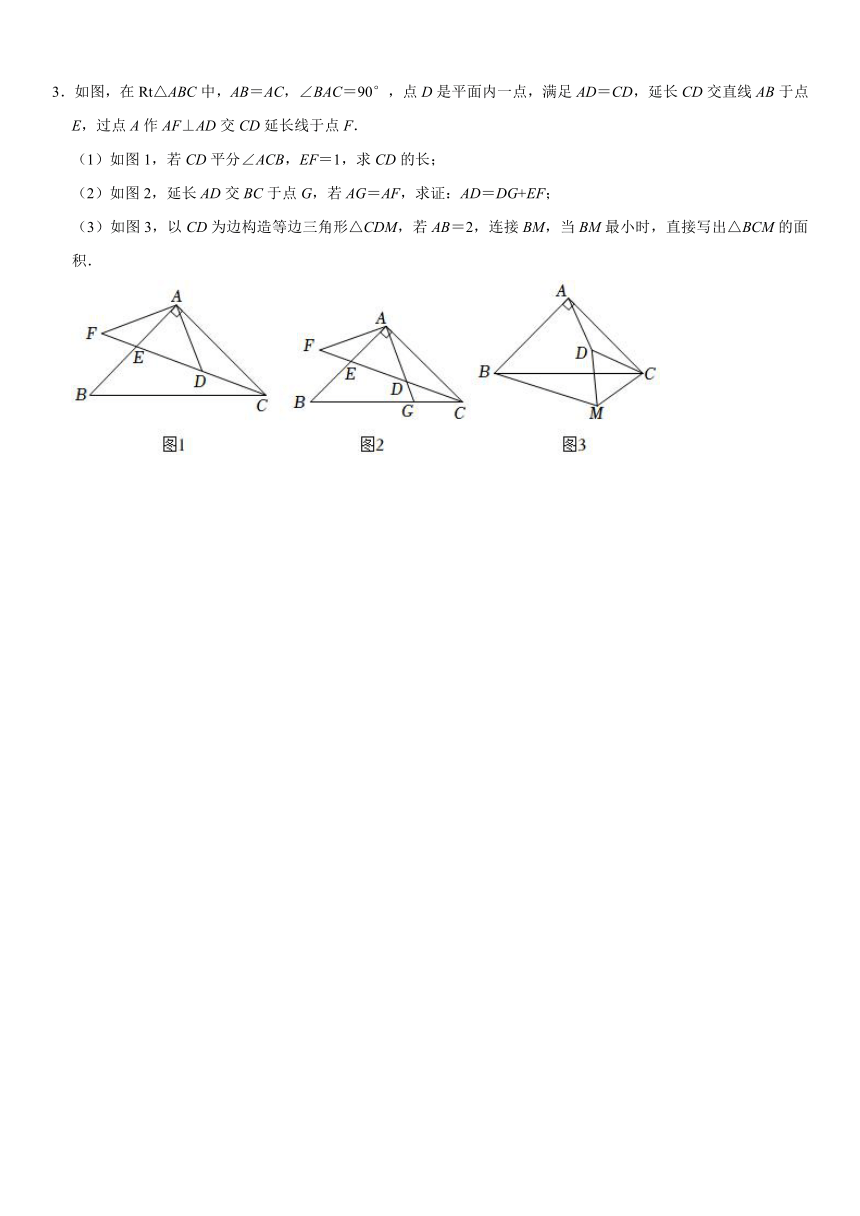
3.如图,在Rt△ABC中,AB=AC,∠BAC=90°,点D是平面内一点,满足AD=CD,延长CD交直线AB于点E,过点A作AF⊥AD交CD延长线于点F.
(1)如图1,若CD平分∠ACB,EF=1,求CD的长;
(2)如图2,延长AD交BC于点G,若AG=AF,求证:AD=DG+EF;
(3)如图3,以CD为边构造等边三角形△CDM,若AB=2,连接BM,当BM最小时,直接写出△BCM的面积.
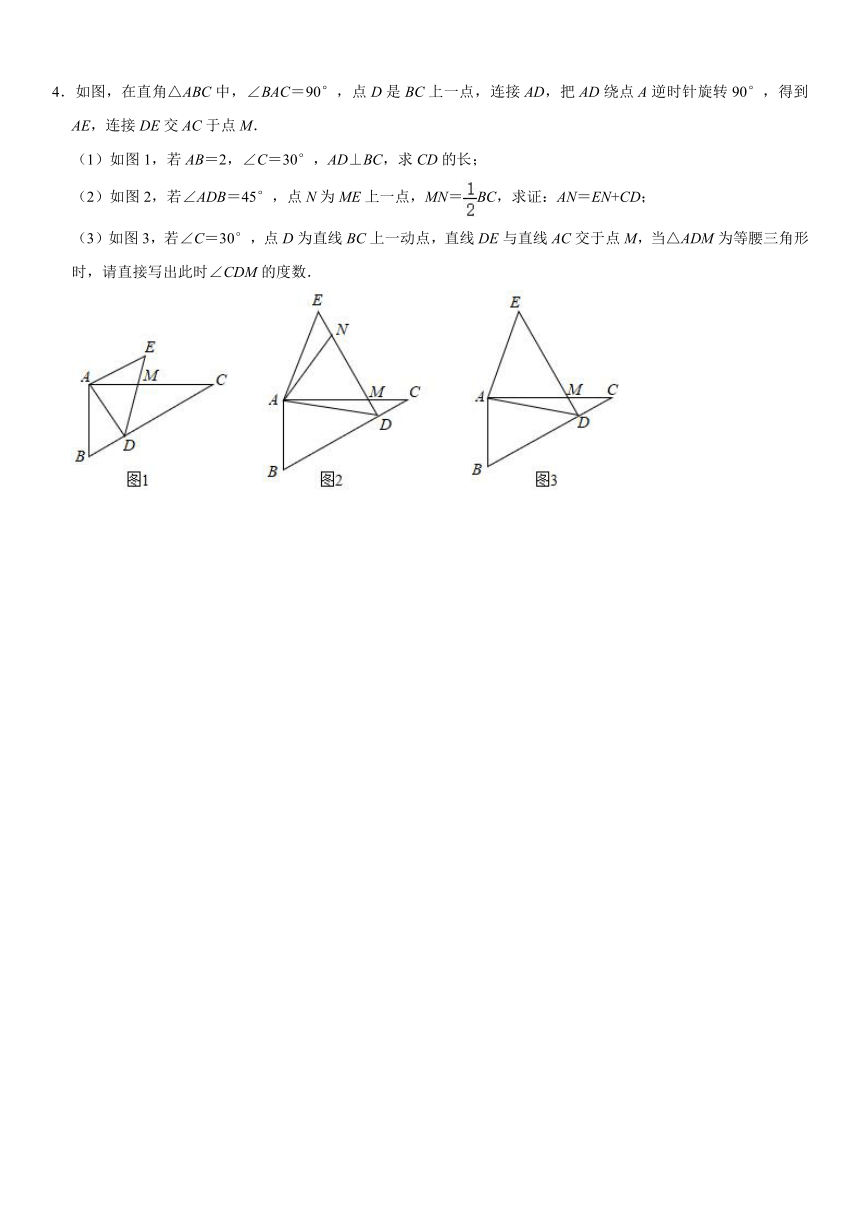
4.如图,在直角△ABC中,∠BAC=90°,点D是BC上一点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接DE交AC于点M.
(1)如图1,若AB=2,∠C=30°,AD⊥BC,求CD的长;
(2)如图2,若∠ADB=45°,点N为ME上一点,MN=BC,求证:AN=EN+CD;
(3)如图3,若∠C=30°,点D为直线BC上一动点,直线DE与直线AC交于点M,当△ADM为等腰三角形时,请直接写出此时∠CDM的度数.
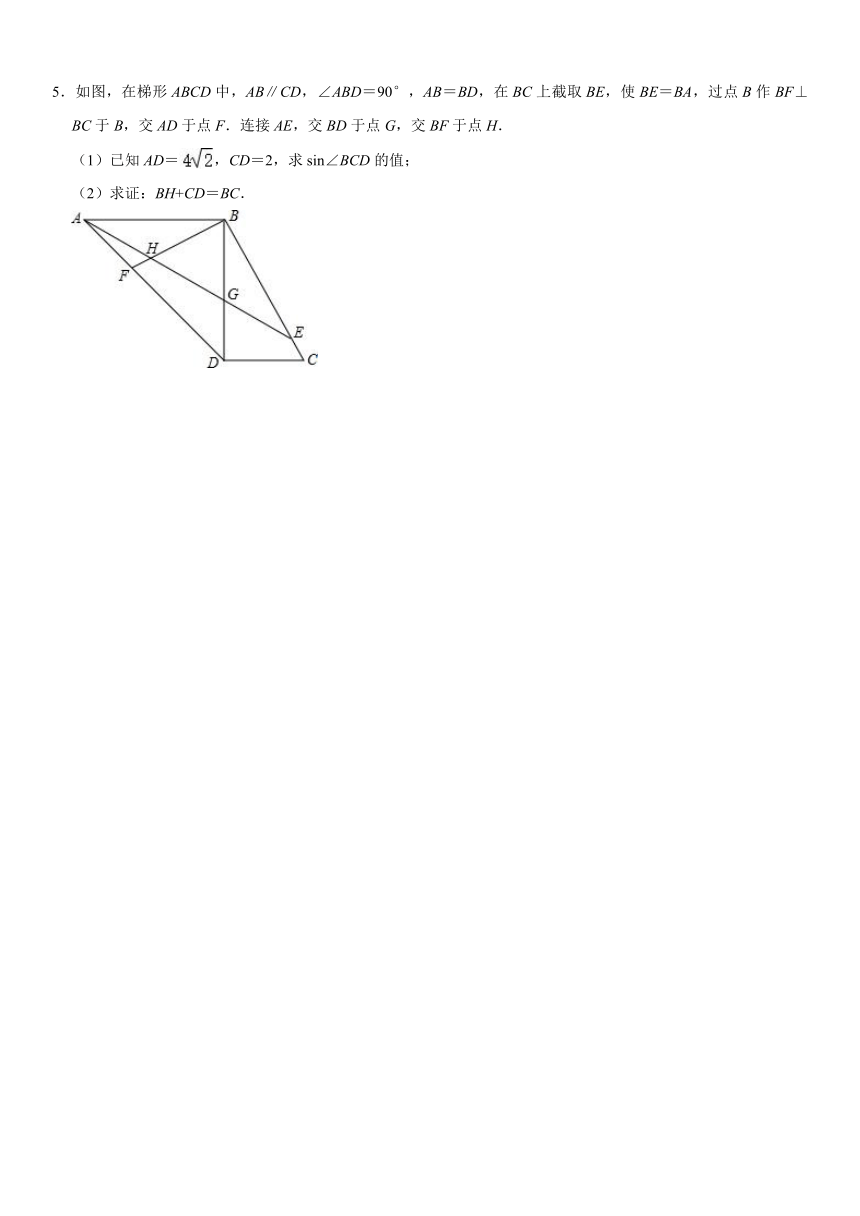
5.如图,在梯形ABCD中,AB∥CD,∠ABD=90°,AB=BD,在BC上截取BE,使BE=BA,过点B作BF⊥BC于B,交AD于点F.连接AE,交BD于点G,交BF于点H.
(1)已知AD=,CD=2,求sin∠BCD的值;
(2)求证:BH+CD=BC.
6.在Rt△ABC中,∠BCA=90°,G为AB的中点,过点G作DG⊥AB交AC于点D.
(1)如图1,连接CG,若CG=,BC=3,求DG的长;
(2)如图2,过点D作DE⊥BD,连接AE,以点E为直角顶点,AE为直角边向外作等腰直角三角形AEF,使得点F刚好落在BD的延长线上,求证:BC=DE+DF.
类型二:倍长中线
7.在等腰Rt△AOB和等腰Rt△DOC中,∠AOB=∠DOC=90°,连AD,M为AD中点,连OM.
(1)如图1,请写出OM与BC的关系,并说明理由;
(2)将图1中的△COD旋转至图2的位置,其他条件不变,(1)中结论是否成立?请说明理由.
8.已知△ABC,△DEC为等腰直角三角形,∠BAC=∠DEC=90°,CD=BC,连接AE,点M是AE的中点.
(1)如图1,若点D在BC边上,连接CM,当CM=4时,求AB的长;
(2)如图2,若点D在△ABC内部,连接BD,点N是BD中点,连接MN,NE,求证:MN=AE.
(3)如图3,若点D在AC边上,连接BD,点N是BD中点,连接MN,直接写出的值.
9.如图,已知在直角△ABC中,∠ABC=90°,E为AC边上一点,连接BE,过E作ED⊥AC,交BC边于点D.
(1)如图1,若tanC=,AE=,AB=EB=2,求S△CED;
(2)如图2,作∠ABC的角平分线交AC于点F,连接DF,若∠BDE=∠CDF,求证:AE+DE=BE;
(3)如图3,在(1)的条件下,M为AB边的中点,G为AC边上一个动点,连接MG,将△AMG沿MG翻折,得到△A'MG,连接A'D,以A'D为斜边向右作等腰直角三角A'DN,连接CN,求CN的最小值.
10.如图,在△ABC中,点D,E分别在BC,AC上,连接AD,AD=DC,点E为AC中点,连接BE交AD于点N,BN=NE.
(1)如图1,若∠ANE=90°,AE=4,求DC的长;
(2)如图2,延长BA至点M,连接ME,AN=ME,若∠ABC=45°,求证:AM+NE=AN;
(3)如图3,延长BA至点M,连接ME,ME=3,∠ADC=∠MEB=90°,点N为AB中点,连接NE,将△BNE沿NE翻折得到△B′NE,点F,G分别为NE,EB′上的动点(不与端点重合),连接AF,FG,连接MG交直线AE于点H,当AF+FG取得最小值时,直接写出的值.
11.如图,已知在直角△ABC中,∠ABC=90°,E为AC边上一点,连接BE,过E作ED⊥AC,交BC边于点D.
(1)如图1,若,求S△AED;
(2)如图2,作∠ABC的角平分线交AC于点F,连接DF,若∠BDE=∠CDF,求证:AE+DE=BE;
(3)如图3,在(1)的条件下,M为AB边的中点,G为AC边上一个动点,连接MG,将△AMG沿MG翻折,得到△A'MG,连接A'D,以A'D为斜边向右作等腰直角三角A'DN,连接CN,求CN的最小值.
12.如图,△ABC中,∠ABC=90°,AB=BC.△CDE中,∠CDE=90°,DC=DE.
(1)图1中,点D是AB上一点,AB=BC=4,BD=1,求CE的长;
(2)图2中,点D是AB上一点,点F是CE的中点,求证:;
(3)图3中,AB=BC=4,点M是BC的中点,点D是平面内一个动点,BD=1,当∠AME的度数最大时,直接写出ME的长度.
13.如图,已知在直角△ABC中,∠ABC=90°,E为AC边上一点,连接BE,过E作ED⊥AC,交BC边于点D.
(1)如图1,连接AD,若CE=2,BD=3,∠C=45°,求△ADE的面积;
(2)如图2,作∠ABC的角平分线交AC于点F,连接DF,若∠BDE=∠CDF,求证:AE+DE=BE;
(3)如图3,若∠C=30°,将△BCE沿BE折叠,得到△BEF,且BF与AC交于点G,连接AD,DF,点E在AC边上运动的过程中,当BF⊥AC时,直接写出的值.
14.如图,在△ABC中,BC>AC,点E在BC上,CE=CA,点D在AB上,连接DE,∠ACB+∠ADE=180°,作CH⊥AB,垂足为H.
(1)如图a,当∠ACB=90°时,连接CD,过点C作CF⊥CD交BA的延长线于点F,求证:FA=DE;
(2)如图b,若∠ACB=120°时,求证:DE+AD=2CH.
15.如图,在△ABC中,AB=AC,点D是BC边上一动点,连接AD.将AD绕点A逆时针旋转,得到AE,满足∠DAE=∠BAC,并连接CE.
(1)如图1,∠BAC=120°,BD=3,CD=9,求AD的长;
(2)如图2,∠BAC=120°,连接BE,F为BE中点,G为CD中点,连接FG,猜想FG和CE存在的数量关系,并证明你猜想的结论;
(3)如图3,∠BAC=135°,BC=m,连接BE,F为BE中点,连接AF,当AF取最小值时,直接用含m的式子表示△BCE的面积.
类型一:截长补短
1.已知:如图,在△ABC中,AB=AC,∠A=100°,BD是∠ABC的平分线,BD=BE.求证:
(1)△CED是等腰三角形;
(2)BD+AD=BC.
2.在Rt△ABC中,∠ABC=90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE.AC=DE,BC=BE.
(1)求证:AB=BD;
(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG.当KB平分∠AKG时,求证:AK=DG+KG.
3.如图,在Rt△ABC中,AB=AC,∠BAC=90°,点D是平面内一点,满足AD=CD,延长CD交直线AB于点E,过点A作AF⊥AD交CD延长线于点F.
(1)如图1,若CD平分∠ACB,EF=1,求CD的长;
(2)如图2,延长AD交BC于点G,若AG=AF,求证:AD=DG+EF;
(3)如图3,以CD为边构造等边三角形△CDM,若AB=2,连接BM,当BM最小时,直接写出△BCM的面积.
4.如图,在直角△ABC中,∠BAC=90°,点D是BC上一点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接DE交AC于点M.
(1)如图1,若AB=2,∠C=30°,AD⊥BC,求CD的长;
(2)如图2,若∠ADB=45°,点N为ME上一点,MN=BC,求证:AN=EN+CD;
(3)如图3,若∠C=30°,点D为直线BC上一动点,直线DE与直线AC交于点M,当△ADM为等腰三角形时,请直接写出此时∠CDM的度数.
5.如图,在梯形ABCD中,AB∥CD,∠ABD=90°,AB=BD,在BC上截取BE,使BE=BA,过点B作BF⊥BC于B,交AD于点F.连接AE,交BD于点G,交BF于点H.
(1)已知AD=,CD=2,求sin∠BCD的值;
(2)求证:BH+CD=BC.
6.在Rt△ABC中,∠BCA=90°,G为AB的中点,过点G作DG⊥AB交AC于点D.
(1)如图1,连接CG,若CG=,BC=3,求DG的长;
(2)如图2,过点D作DE⊥BD,连接AE,以点E为直角顶点,AE为直角边向外作等腰直角三角形AEF,使得点F刚好落在BD的延长线上,求证:BC=DE+DF.
类型二:倍长中线
7.在等腰Rt△AOB和等腰Rt△DOC中,∠AOB=∠DOC=90°,连AD,M为AD中点,连OM.
(1)如图1,请写出OM与BC的关系,并说明理由;
(2)将图1中的△COD旋转至图2的位置,其他条件不变,(1)中结论是否成立?请说明理由.
8.已知△ABC,△DEC为等腰直角三角形,∠BAC=∠DEC=90°,CD=BC,连接AE,点M是AE的中点.
(1)如图1,若点D在BC边上,连接CM,当CM=4时,求AB的长;
(2)如图2,若点D在△ABC内部,连接BD,点N是BD中点,连接MN,NE,求证:MN=AE.
(3)如图3,若点D在AC边上,连接BD,点N是BD中点,连接MN,直接写出的值.
9.如图,已知在直角△ABC中,∠ABC=90°,E为AC边上一点,连接BE,过E作ED⊥AC,交BC边于点D.
(1)如图1,若tanC=,AE=,AB=EB=2,求S△CED;
(2)如图2,作∠ABC的角平分线交AC于点F,连接DF,若∠BDE=∠CDF,求证:AE+DE=BE;
(3)如图3,在(1)的条件下,M为AB边的中点,G为AC边上一个动点,连接MG,将△AMG沿MG翻折,得到△A'MG,连接A'D,以A'D为斜边向右作等腰直角三角A'DN,连接CN,求CN的最小值.
10.如图,在△ABC中,点D,E分别在BC,AC上,连接AD,AD=DC,点E为AC中点,连接BE交AD于点N,BN=NE.
(1)如图1,若∠ANE=90°,AE=4,求DC的长;
(2)如图2,延长BA至点M,连接ME,AN=ME,若∠ABC=45°,求证:AM+NE=AN;
(3)如图3,延长BA至点M,连接ME,ME=3,∠ADC=∠MEB=90°,点N为AB中点,连接NE,将△BNE沿NE翻折得到△B′NE,点F,G分别为NE,EB′上的动点(不与端点重合),连接AF,FG,连接MG交直线AE于点H,当AF+FG取得最小值时,直接写出的值.
11.如图,已知在直角△ABC中,∠ABC=90°,E为AC边上一点,连接BE,过E作ED⊥AC,交BC边于点D.
(1)如图1,若,求S△AED;
(2)如图2,作∠ABC的角平分线交AC于点F,连接DF,若∠BDE=∠CDF,求证:AE+DE=BE;
(3)如图3,在(1)的条件下,M为AB边的中点,G为AC边上一个动点,连接MG,将△AMG沿MG翻折,得到△A'MG,连接A'D,以A'D为斜边向右作等腰直角三角A'DN,连接CN,求CN的最小值.
12.如图,△ABC中,∠ABC=90°,AB=BC.△CDE中,∠CDE=90°,DC=DE.
(1)图1中,点D是AB上一点,AB=BC=4,BD=1,求CE的长;
(2)图2中,点D是AB上一点,点F是CE的中点,求证:;
(3)图3中,AB=BC=4,点M是BC的中点,点D是平面内一个动点,BD=1,当∠AME的度数最大时,直接写出ME的长度.
13.如图,已知在直角△ABC中,∠ABC=90°,E为AC边上一点,连接BE,过E作ED⊥AC,交BC边于点D.
(1)如图1,连接AD,若CE=2,BD=3,∠C=45°,求△ADE的面积;
(2)如图2,作∠ABC的角平分线交AC于点F,连接DF,若∠BDE=∠CDF,求证:AE+DE=BE;
(3)如图3,若∠C=30°,将△BCE沿BE折叠,得到△BEF,且BF与AC交于点G,连接AD,DF,点E在AC边上运动的过程中,当BF⊥AC时,直接写出的值.
14.如图,在△ABC中,BC>AC,点E在BC上,CE=CA,点D在AB上,连接DE,∠ACB+∠ADE=180°,作CH⊥AB,垂足为H.
(1)如图a,当∠ACB=90°时,连接CD,过点C作CF⊥CD交BA的延长线于点F,求证:FA=DE;
(2)如图b,若∠ACB=120°时,求证:DE+AD=2CH.
15.如图,在△ABC中,AB=AC,点D是BC边上一动点,连接AD.将AD绕点A逆时针旋转,得到AE,满足∠DAE=∠BAC,并连接CE.
(1)如图1,∠BAC=120°,BD=3,CD=9,求AD的长;
(2)如图2,∠BAC=120°,连接BE,F为BE中点,G为CD中点,连接FG,猜想FG和CE存在的数量关系,并证明你猜想的结论;
(3)如图3,∠BAC=135°,BC=m,连接BE,F为BE中点,连接AF,当AF取最小值时,直接用含m的式子表示△BCE的面积.
同课章节目录
