山西省浑源中学2022-2023学年高二下学期期末考试数学试卷(含解析)
文档属性
| 名称 | 山西省浑源中学2022-2023学年高二下学期期末考试数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 742.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-17 20:48:16 | ||
图片预览




文档简介
山西省浑源中学2022-2023学年高二下学期期末考试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、已知集合,,则( )
A. B. C. D.
2、设函数,则“”是“在上单调递增”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3、已知,若关于x的方程有3个不同实根,则实数a取值范围为( )
A. B. C. D.
4、已知平面向量,满足,则在上的投影向量为( )
A. B. C. D.
5、在中,点O满足,过点O的直线分别交射线AB,AC于点M,N,且,,则的最小值为( )
A. B. C.3 D.4
6、三面角是立体几何的重要概念之一.三面角是指由有公共端点P且不共面的三条射线PA,PB,PC以及相邻两射线之间的平面部分所组成的空间图形.三面角余弦定理告诉我们,若,,,平面APC与平面BPC所成夹角为,则.现已知三棱锥,,,,,,则当三棱锥的体积最大时,它的外接球的表面积为( )
A. B. C. D.
7、已知函数在处取得极大值10,则的值为( )
A. B.或2 C.2 D.
8、设F为双曲线(,)的右焦点,O为坐标原点,以OF为直径的圆与圆交于P,Q两点.若,则C的离心率为( )
A. B. C.2 D.
9、若函数的最小值是-1,则实数m的取值范围是( )
A. B. C. D.
10、已知椭圆的左右焦点分别为,,点M是椭圆C上任意一点,且的取值范围为,当点M不在x轴上时,设的内切圆半径为m,外接圆半径为n,则mn的最大值为( )
A.1 B. C. D.
11、设随机变量,若,则( )
A. B. C. D.
12、三位同学获得本年度数学竞赛前三名,老师告知他们如下信息:
①甲是第三名;
②乙不是第一名;
③丙不是第三名,并告知他们以上3条信息有且只有1条是正确信息,则该三位同学的数学竞赛成绩从高到低的排序为( )
A.甲,乙,丙 B.丙,乙,甲 C.乙,丙,甲 D.乙,甲,丙
二、填空题
13、已知具有相关关系的两个变量x,y的一组观测数据如下表所示,若据此利用最小二乘估计得到回归方程,则_______.
x 3 4 5 6
y 2.5 m 4 4.5
14、有穷等差数列的各项均为正数,若,则的最小值是_________.
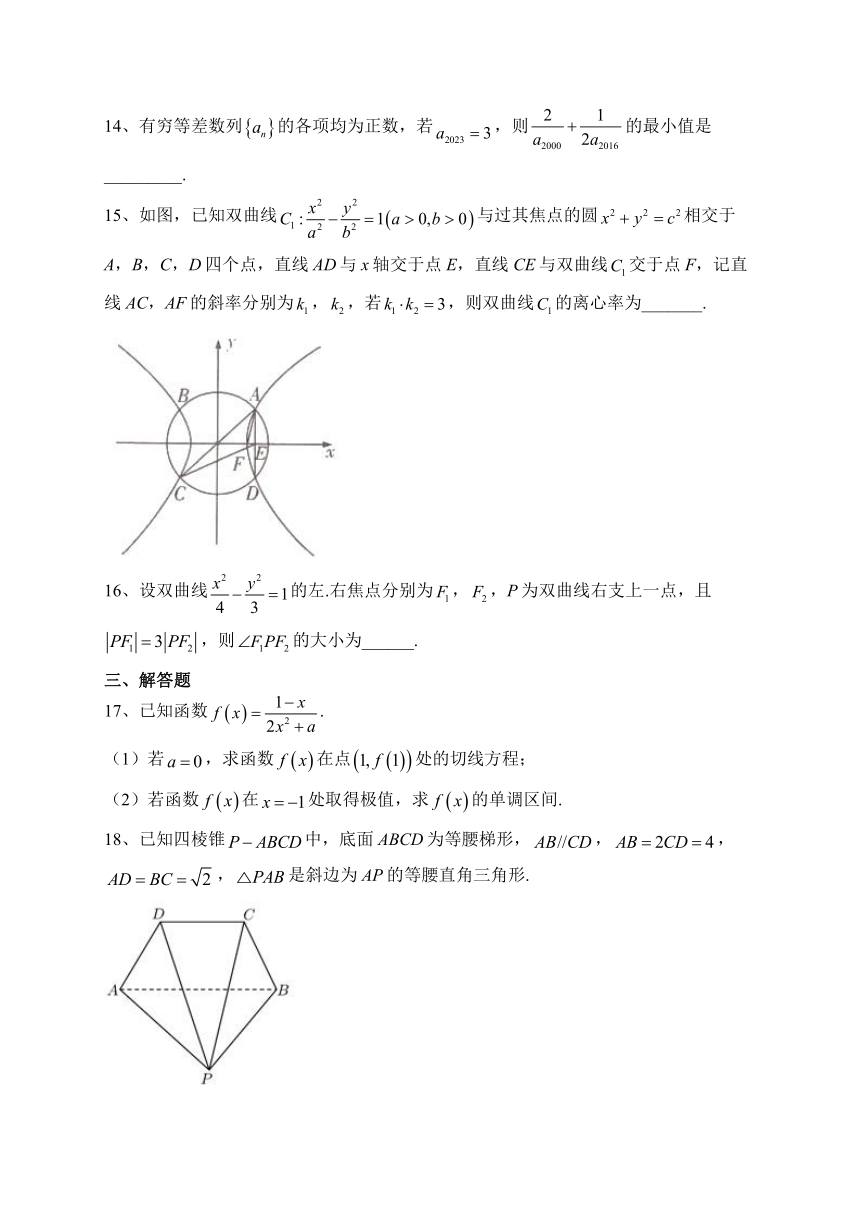
15、如图,已知双曲线与过其焦点的圆相交于A,B,C,D四个点,直线AD与x轴交于点E,直线CE与双曲线交于点F,记直线AC,AF的斜率分别为,,若,则双曲线的离心率为_______.
16、设双曲线的左.右焦点分别为,,P为双曲线右支上一点,且,则的大小为______.
三、解答题
17、已知函数.
(1)若,求函数在点处的切线方程;
(2)若函数在处取得极值,求的单调区间.
18、已知四棱锥中,底面ABCD为等腰梯形,,,,是斜边为AP的等腰直角三角形.
(1)若时,求证:平面平面ABCD;
(2)若时,求直线PD与平面ABCD所成的角的正弦值.
19、在数列中,,.
(1)证明是等比数列;
(2)若,求数列的前n项和.
20、根据交管部门有关规定,驾驶电动自行车必须佩戴头盔,保护自身安全,某市去年上半年对此不断进行安全教育.下表是该市某主干路口去年连续5个月监控设备抓拍到的电动自行车驾驶员不戴头盔的统计数据:
月份x 1 2 3 4 5
不戴头盔人数y 120 100 90 75 65
(1)请利用所给数据求不戴头盔人数y与月份x之间的回归直线方程;
(2)交管部门统计连续5年来通过该路口的电动车出事故的100人,分析不戴头盔行为与事故是否伤亡的关系得到下表,从表中数据能否有95%的把握认为不戴头盔行为与事故伤亡有关?
不戴头盔 戴头盔
伤亡 15 10
不伤亡 25 50
参考数据和公式:,,
0.10 0.05 0.01 0.005
k 2.706 3.841 6.635 7.879
21、某公司组织本单位员工参加抽奖得消费优惠券活动,抽奖规则是:每人从装有质地均匀.大小相同的4个黄球.4个红球的箱子中一次性地随机摸出3个球,若恰有1个红球可获得50元优惠券,恰有2个红球可获得100元优惠券,3个都是红球可获得200元优惠券,其他情况无优惠券.小王参加了公司的抽奖活动.
(1)求小王恰好摸出1个黄球的概率;
(2)设小王获得的优惠券金额为X,求X的分布列与期望.
22、已知
(1)若,求的极值;
(2)若,,,且,其中,,求证:.
参考答案
1、答案:C
解析:因为集合 ,所以. 故选: C.
2、答案:A
解析:因为 在上单调递 增,
所以由复合函数的单调性可知,,所以“”是“”的充分不必要条件.
故选:A.
3、答案:D
解析:
4、答案:A
解析:由 知:
, 可得,
所以 在上的投影向量为.
故选: A.
5、答案:A
解析:
6、答案:B
解析:由题知, ,,,
平面APC与平面BPC所成夹角为,
作,平面APC,则,
由题意得 ,
,,
,
,
所以
要使三棱锥 的体积最大,则最大,
在中,由余弦定理得,
整理得,,,
即,
当且仅当,时,等号成立,
则,,
因为$
解得,
所以,
,
即,,
所以补全三棱锥成棱柱,如下图,
则四边形BCPD是菱形,
点O为其外接球的球心,即AD中点,
所以,
所以外接球半径为3,
即三棱锥外接球的表面积为.
故选:B.
7、答案:A
解析:
8、答案:A
解析:设双曲线C的焦距为, 则 则线段OF的中点为,
.
则以OF为直径的圆的圆心为,半径为,
所以以OF为直径的圆的方程为
即,
联立,消去二次项得
直线PQ的方程为,
圆圆心为O,半径为a,
因为O到直线PQ的距离,
所以
所以,
所以,
所以,
所以,
则,
所以双曲线的离心率为.
故选:A.
9、答案:A
解析:当 时,,
,
,,单调递减,
,,单调递
增,,
因为 的最小值为-1 ,所以当
时,,
当时,.
①若,在上单调递减, ,
,得;
②若,在上单调递减,在上单调递增,,舍去.
综上,实数m的取值范围是.
故选: B.
10、答案:B
解析:
11、答案:D
解析:因为,,所以,
即, 解得,即, 所以,
故选D.
12、答案:A
解析:若①正确,②③不正确,即甲是第三名,乙是第一名,丙是第三名,则甲丙都是第三名,矛盾;若②
正确①③不正确,即甲不是第三名,乙不是第一名,丙是第三名,则甲是第一名,乙是第二名,丙是第三名;
若③正确,①②不正确,即甲不是第三名,乙是第一名,丙不是第三名,此时没有人是第三名,不符合题意
综上,甲是第一名,乙是第二名,丙是第三名.故选A.
13、答案:3
解析:,所以样本中心点为:.
因为回归方程, 样本中心点在回归方程上,
所以,解得:.
故答案为:3.
14、答案:
解析:由,且,
则
,当且仅当,时等号成立且满足题 设.
故答案为:
15、答案:
解析:
16、答案:
解析:因为双曲线 ,则,,
所以,
因为P为双曲线右支上一点,所以,
又,
所以,
又 ,
由余弦定理,
即,
解得,
又,
所以.
故答案为:
17、答案:(1)
(2)的单调递增区间为,,的单调递减区间为
解析:(1)因为所以.
所以,所以,
又,
所以曲线在点处的切线方程为:
(2)由函数在处取得极值可知:
,即,解得:
此时,,,
当时,,
当时,,
所以符合题意.
综上,的单调递增区间为,,的单调递减区间为.
18、答案:(1)见解析
(2)
解析:(1)因,,,则有,即有,
又,且,AB,平面ABCD,
于是得平面ABCD,而平面PBC,
所以平面平面ABCD.
(2)在平面ABCD内,过B作直线垂直于AB,交直线CD于E,有,,
如图,
则为二面角的平面角,平面EBC,,于是得,
中,,则,在中,,,,
由余弦定理得,则有,
显然平面平面EBP,在平面EBP内过B作,则平面ABP,
以B为原点,分别以射线BA,BP,Bz为x,y,z轴非负半轴建立空间直角坐标系,
则,,,,,,,
设平面ABCD的法向量,则,
令,得
而,设PD与平面ABCD所成的角为,
所以PD与平面ABCD所成的角的正弦值为.
19、答案:(1)证明见解析
(2)答案见解析
解析:(1)由已知可得,
∴.
所以是以2为首项,2为公比的等比数列.
(2)由(1)可得,因此,,
.
20、答案:(1)
(2)答案见解析
解析:(1)由题意知,
,,
,
所以,回归直线方程为
(2)
故有的把握认为不戴头盔行为与事故伤亡有关.
21、答案:(1)
(2)分布列见解析,
解析:(1)记事件A:小王恰好摸出1个黄球,则
(2)由题意,得X的可能取值为0,50,100,200,
,,,
所以X的分布列为
X 0 50 100 200
P
所以.
22、答案:(1)当时,取得极大值,极大值为;无极小值
(2)证明见解析
解析:(1)由题:,,
令,解得,列表如图:
x 3
0
单调递增 单调递减
故当时,取得极大值,
极大值为;无极小值.
(2)若,则,结论成立;
若,,令,得,当时,,
故在单调递增.
要证,只需证,又,,且在单调递增,故只需证明,又因为,
故只需证明,
由,
故只需证明:
令,只需证,
,在单调递增,.证毕.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、已知集合,,则( )
A. B. C. D.
2、设函数,则“”是“在上单调递增”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3、已知,若关于x的方程有3个不同实根,则实数a取值范围为( )
A. B. C. D.
4、已知平面向量,满足,则在上的投影向量为( )
A. B. C. D.
5、在中,点O满足,过点O的直线分别交射线AB,AC于点M,N,且,,则的最小值为( )
A. B. C.3 D.4
6、三面角是立体几何的重要概念之一.三面角是指由有公共端点P且不共面的三条射线PA,PB,PC以及相邻两射线之间的平面部分所组成的空间图形.三面角余弦定理告诉我们,若,,,平面APC与平面BPC所成夹角为,则.现已知三棱锥,,,,,,则当三棱锥的体积最大时,它的外接球的表面积为( )
A. B. C. D.
7、已知函数在处取得极大值10,则的值为( )
A. B.或2 C.2 D.
8、设F为双曲线(,)的右焦点,O为坐标原点,以OF为直径的圆与圆交于P,Q两点.若,则C的离心率为( )
A. B. C.2 D.
9、若函数的最小值是-1,则实数m的取值范围是( )
A. B. C. D.
10、已知椭圆的左右焦点分别为,,点M是椭圆C上任意一点,且的取值范围为,当点M不在x轴上时,设的内切圆半径为m,外接圆半径为n,则mn的最大值为( )
A.1 B. C. D.
11、设随机变量,若,则( )
A. B. C. D.
12、三位同学获得本年度数学竞赛前三名,老师告知他们如下信息:
①甲是第三名;
②乙不是第一名;
③丙不是第三名,并告知他们以上3条信息有且只有1条是正确信息,则该三位同学的数学竞赛成绩从高到低的排序为( )
A.甲,乙,丙 B.丙,乙,甲 C.乙,丙,甲 D.乙,甲,丙
二、填空题
13、已知具有相关关系的两个变量x,y的一组观测数据如下表所示,若据此利用最小二乘估计得到回归方程,则_______.
x 3 4 5 6
y 2.5 m 4 4.5
14、有穷等差数列的各项均为正数,若,则的最小值是_________.
15、如图,已知双曲线与过其焦点的圆相交于A,B,C,D四个点,直线AD与x轴交于点E,直线CE与双曲线交于点F,记直线AC,AF的斜率分别为,,若,则双曲线的离心率为_______.
16、设双曲线的左.右焦点分别为,,P为双曲线右支上一点,且,则的大小为______.
三、解答题
17、已知函数.
(1)若,求函数在点处的切线方程;
(2)若函数在处取得极值,求的单调区间.
18、已知四棱锥中,底面ABCD为等腰梯形,,,,是斜边为AP的等腰直角三角形.
(1)若时,求证:平面平面ABCD;
(2)若时,求直线PD与平面ABCD所成的角的正弦值.
19、在数列中,,.
(1)证明是等比数列;
(2)若,求数列的前n项和.
20、根据交管部门有关规定,驾驶电动自行车必须佩戴头盔,保护自身安全,某市去年上半年对此不断进行安全教育.下表是该市某主干路口去年连续5个月监控设备抓拍到的电动自行车驾驶员不戴头盔的统计数据:
月份x 1 2 3 4 5
不戴头盔人数y 120 100 90 75 65
(1)请利用所给数据求不戴头盔人数y与月份x之间的回归直线方程;
(2)交管部门统计连续5年来通过该路口的电动车出事故的100人,分析不戴头盔行为与事故是否伤亡的关系得到下表,从表中数据能否有95%的把握认为不戴头盔行为与事故伤亡有关?
不戴头盔 戴头盔
伤亡 15 10
不伤亡 25 50
参考数据和公式:,,
0.10 0.05 0.01 0.005
k 2.706 3.841 6.635 7.879
21、某公司组织本单位员工参加抽奖得消费优惠券活动,抽奖规则是:每人从装有质地均匀.大小相同的4个黄球.4个红球的箱子中一次性地随机摸出3个球,若恰有1个红球可获得50元优惠券,恰有2个红球可获得100元优惠券,3个都是红球可获得200元优惠券,其他情况无优惠券.小王参加了公司的抽奖活动.
(1)求小王恰好摸出1个黄球的概率;
(2)设小王获得的优惠券金额为X,求X的分布列与期望.
22、已知
(1)若,求的极值;
(2)若,,,且,其中,,求证:.
参考答案
1、答案:C
解析:因为集合 ,所以. 故选: C.
2、答案:A
解析:因为 在上单调递 增,
所以由复合函数的单调性可知,,所以“”是“”的充分不必要条件.
故选:A.
3、答案:D
解析:
4、答案:A
解析:由 知:
, 可得,
所以 在上的投影向量为.
故选: A.
5、答案:A
解析:
6、答案:B
解析:由题知, ,,,
平面APC与平面BPC所成夹角为,
作,平面APC,则,
由题意得 ,
,,
,
,
所以
要使三棱锥 的体积最大,则最大,
在中,由余弦定理得,
整理得,,,
即,
当且仅当,时,等号成立,
则,,
因为$
解得,
所以,
,
即,,
所以补全三棱锥成棱柱,如下图,
则四边形BCPD是菱形,
点O为其外接球的球心,即AD中点,
所以,
所以外接球半径为3,
即三棱锥外接球的表面积为.
故选:B.
7、答案:A
解析:
8、答案:A
解析:设双曲线C的焦距为, 则 则线段OF的中点为,
.
则以OF为直径的圆的圆心为,半径为,
所以以OF为直径的圆的方程为
即,
联立,消去二次项得
直线PQ的方程为,
圆圆心为O,半径为a,
因为O到直线PQ的距离,
所以
所以,
所以,
所以,
所以,
则,
所以双曲线的离心率为.
故选:A.
9、答案:A
解析:当 时,,
,
,,单调递减,
,,单调递
增,,
因为 的最小值为-1 ,所以当
时,,
当时,.
①若,在上单调递减, ,
,得;
②若,在上单调递减,在上单调递增,,舍去.
综上,实数m的取值范围是.
故选: B.
10、答案:B
解析:
11、答案:D
解析:因为,,所以,
即, 解得,即, 所以,
故选D.
12、答案:A
解析:若①正确,②③不正确,即甲是第三名,乙是第一名,丙是第三名,则甲丙都是第三名,矛盾;若②
正确①③不正确,即甲不是第三名,乙不是第一名,丙是第三名,则甲是第一名,乙是第二名,丙是第三名;
若③正确,①②不正确,即甲不是第三名,乙是第一名,丙不是第三名,此时没有人是第三名,不符合题意
综上,甲是第一名,乙是第二名,丙是第三名.故选A.
13、答案:3
解析:,所以样本中心点为:.
因为回归方程, 样本中心点在回归方程上,
所以,解得:.
故答案为:3.
14、答案:
解析:由,且,
则
,当且仅当,时等号成立且满足题 设.
故答案为:
15、答案:
解析:
16、答案:
解析:因为双曲线 ,则,,
所以,
因为P为双曲线右支上一点,所以,
又,
所以,
又 ,
由余弦定理,
即,
解得,
又,
所以.
故答案为:
17、答案:(1)
(2)的单调递增区间为,,的单调递减区间为
解析:(1)因为所以.
所以,所以,
又,
所以曲线在点处的切线方程为:
(2)由函数在处取得极值可知:
,即,解得:
此时,,,
当时,,
当时,,
所以符合题意.
综上,的单调递增区间为,,的单调递减区间为.
18、答案:(1)见解析
(2)
解析:(1)因,,,则有,即有,
又,且,AB,平面ABCD,
于是得平面ABCD,而平面PBC,
所以平面平面ABCD.
(2)在平面ABCD内,过B作直线垂直于AB,交直线CD于E,有,,
如图,
则为二面角的平面角,平面EBC,,于是得,
中,,则,在中,,,,
由余弦定理得,则有,
显然平面平面EBP,在平面EBP内过B作,则平面ABP,
以B为原点,分别以射线BA,BP,Bz为x,y,z轴非负半轴建立空间直角坐标系,
则,,,,,,,
设平面ABCD的法向量,则,
令,得
而,设PD与平面ABCD所成的角为,
所以PD与平面ABCD所成的角的正弦值为.
19、答案:(1)证明见解析
(2)答案见解析
解析:(1)由已知可得,
∴.
所以是以2为首项,2为公比的等比数列.
(2)由(1)可得,因此,,
.
20、答案:(1)
(2)答案见解析
解析:(1)由题意知,
,,
,
所以,回归直线方程为
(2)
故有的把握认为不戴头盔行为与事故伤亡有关.
21、答案:(1)
(2)分布列见解析,
解析:(1)记事件A:小王恰好摸出1个黄球,则
(2)由题意,得X的可能取值为0,50,100,200,
,,,
所以X的分布列为
X 0 50 100 200
P
所以.
22、答案:(1)当时,取得极大值,极大值为;无极小值
(2)证明见解析
解析:(1)由题:,,
令,解得,列表如图:
x 3
0
单调递增 单调递减
故当时,取得极大值,
极大值为;无极小值.
(2)若,则,结论成立;
若,,令,得,当时,,
故在单调递增.
要证,只需证,又,,且在单调递增,故只需证明,又因为,
故只需证明,
由,
故只需证明:
令,只需证,
,在单调递增,.证毕.
同课章节目录
