2.1整式(第1课时) 课件(24张PPT)
文档属性
| 名称 | 2.1整式(第1课时) 课件(24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 09:13:57 | ||
图片预览








文档简介
(共24张PPT)
第2.1 整式
(第1课时)
人教版数学七年级上册
1.理解字母表示数的意义,经历探索规律的过程,并用代数式表示数量关系和运算规律,学会用字母表示公式和法则.
2.理解单项式的有关概念. 3.通过单项式概念形成过程的教学,培养学生分析归纳问题的能力.
学习目标
青藏铁路西线上,在格尔木到拉萨之间有一段很长的冻土地段. 列车在冻土地段、非冻土地段的行驶速度分别是100千米/时和120千米/时,请根据这些数据回答:
(1)列车在冻土地段行驶时,2小时能行驶多少千米?3小时呢?t小时呢?
情境引入
我们来看本章引言中的问题(1).
列车在冻土地段的行驶速度是100千米/时,根据:路程=速度×时间
列车2h行驶的路程是:100×2=200(km)
列车3h行驶的路程是:100×3=300(km)
列车th行驶的路程是:100×t=100t(km) ①
那么th行驶的路程呢?
通常将乘号写作“·”或省略不屑.例如,100×t可以写成100·t或100t.
互动新授
例1 (1)苹果原价是每千克a元,按8折优惠出售,用式子表示现价;
(2)某产品前年的产量是n件,去年的产量是前年产量的m倍,用式子表示去年的产量;
(3)一个长方体包装盒的长和宽都是a cm,高是h cm,用式子表示它的体积;
(4)用式子表示数n的相反数.
解:(1)现价是每千克0.8p元;
(2)去年的产量是mn件;
(3)由长方体的体积=长×宽×高,得这个长方体包装盒的体积是a a h cm3,即a2h cm3;
(4)数n的相反数是-n.
典例精析
例2 (1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
顺水速度=静水速度+水流速度
逆水速度=静水速度-水流速度
解:船在这条河中顺水行驶的速度是(v+2.5)km/h,
提示:带单位时,适当加括号
分析:
典例精析
例2 (2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,用式子表示买3个篮球、5个排球、2个足球共需要的钱数;
分析:总钱数= 3个篮球的钱数+5个排球的钱数+ 2个足球的钱数.总价=单价×数量
解:买3个篮球、5个排球、2个足球共需要(3x+5y+2z) 元.
典例精析
例2 (3)如下图(图中长度单位:cm),用式子表示三角尺的面积;
分析:三角尺的面积=三角形的面积-圆的面积
三角形的面积= 底×高
圆的面积=
解:三角尺的面积是
典例精析
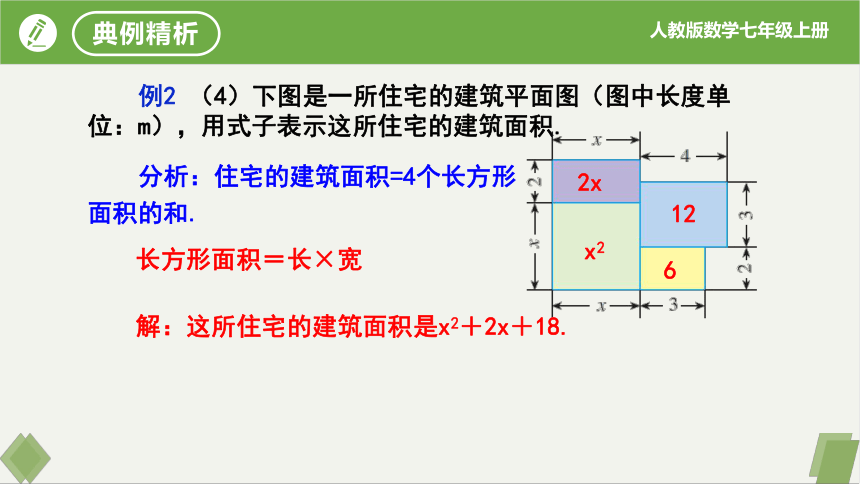
例2 (4)下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
分析:住宅的建筑面积=4个长方形面积的和.
长方形面积=长×宽
解:这所住宅的建筑面积是x2+2x+18.
2x
x2
12
6
典例精析
观察式子100t,0.8p,mn,a2h,-n,都有哪些特点?
100t
0.8p
a2h
mn
-n
数
字母
相乘
相乘
数
字母
相乘
字母
字母
你发现这些式子有什么共同特点?
这些式子都是数或字母的积,像这样的式子叫做单项式.单独的一个数或一个字母也是单项式.
互动新授
单项式中的数字因数叫做这个单项式的系数.
例如,单项式100t,a2h,-n的系数分别是100,1,-1.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
例如,在单项式100t中字母t的指数是1,100t的次数是1.
那么单项式a2h的次数是多少呢?
字母a与h的指数的和是3,a2h的次数是3.
互动新授
例3 用单项式填空,并指出它们的系数和次数:
(1) 每包书有12册,n包书有______册;
(2) 底边长为acm,高为hcm的三角形的面积是_____ cm2;
(3) 棱长为acm的正方体的体积是____cm3 ;
12n
a3
解:(1)系数是12,次数是1.
(2)系数是 ,次数是2.
(3)系数是1,次数是3.
典例精析
例3 用单项式填空,并指出它们的系数和次数:
(4)一台电视机原价 b 元,现按原价的9折出售,这台电视机现在的售价是_____元;
(5)一个长方形的长是0.9 m,宽是b m ,这个长方形的面积是_____m2.
0.9b
解:(4)系数是0.9,次数是1.
0.9b
(5)系数是0.9,次数是1.
典例精析
小试牛刀
1.在括号里填上适当的式子.
(1)小明的体重38千克,小红比小明重a千克,小红的体重是( )千克.
(2)乐乐有20元钱,买文具用去了a元,还剩下( )元.
(3)每千克苹果y元,买3千克苹果需要( )元.
(4)把x个玩具分给b个小朋友,每个小朋友分得玩具( )个.
(5)地球的直径是m万千米,太阳的直径是地球直径的109倍,太阳的直径是( )万千米.
38+a
20-a
3y
109m
2.用代数式填空
⑵我国去年一户农民平均收入为n万元,今年比去年增长了30﹪,今年收入为______ 万元.
⑴长方形的面积为S,宽为a,则其长为_____.
⑶一圆形花坛半径为r,则其面积为______ .
⑷规定向东为正方向,小明向东走了b米,花花向西走的路程是小明的2y倍,则花花走了______米.
⑸体重由m千克减了4千克之后是_______千克.
1.3n
-2by
(m-4)
小试牛刀
1.下面各题的判断是否正确。
①-2xy2的系数是2; ( )
②m4y3与-x3没有系数 ; ( )
③-ab2c3的次数是0+2+3; ( )
④-a5的系数是-1; ( )
⑤ πr2h的系数是 。 ( )
⑥-2nx2y2的系数是-2n,次数为4. ( )
×
×
×
×
√
×
课堂检测
课堂检测
②③⑥
四次
四次
六次
3ab3
-3
-2
6
课堂检测
拓展训练
D
拓展训练
2.已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2﹣3ab的值.
解:因为x2y|a|+(b+2)是关于x,y的五次单项式,
所以b+2=0,2+|a|=5
所以a=±3,b=-2
则当a=﹣3,b=﹣2时,a2﹣3ab=9﹣18=﹣9;
当a=3,b=﹣2时,a2﹣3ab=9+18=27.
这些式子都是数或字母的积,像这样的式子叫做单项式.单独的一个数或一个字母也是单项式.
单项式:
单项式中的数字因数叫做这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
系数:
单项式的次数:
课堂小结
课后作业
B
A
3.电影院里座位的总排数是m,若第一排的座位数是a,并且后一排总比前一排的座位数多1个,则电影院里第m排有多少个座位?
解:因为共有m排座位,且后一排总比前一排的座位数多1个
所以第一排有a个座位,
第二排有(a+1)个座位,
第三排有(a+2)个座位,…
第m排有(a+m-1)个座位.
课后作业
谢谢聆听
第2.1 整式
(第1课时)
人教版数学七年级上册
1.理解字母表示数的意义,经历探索规律的过程,并用代数式表示数量关系和运算规律,学会用字母表示公式和法则.
2.理解单项式的有关概念. 3.通过单项式概念形成过程的教学,培养学生分析归纳问题的能力.
学习目标
青藏铁路西线上,在格尔木到拉萨之间有一段很长的冻土地段. 列车在冻土地段、非冻土地段的行驶速度分别是100千米/时和120千米/时,请根据这些数据回答:
(1)列车在冻土地段行驶时,2小时能行驶多少千米?3小时呢?t小时呢?
情境引入
我们来看本章引言中的问题(1).
列车在冻土地段的行驶速度是100千米/时,根据:路程=速度×时间
列车2h行驶的路程是:100×2=200(km)
列车3h行驶的路程是:100×3=300(km)
列车th行驶的路程是:100×t=100t(km) ①
那么th行驶的路程呢?
通常将乘号写作“·”或省略不屑.例如,100×t可以写成100·t或100t.
互动新授
例1 (1)苹果原价是每千克a元,按8折优惠出售,用式子表示现价;
(2)某产品前年的产量是n件,去年的产量是前年产量的m倍,用式子表示去年的产量;
(3)一个长方体包装盒的长和宽都是a cm,高是h cm,用式子表示它的体积;
(4)用式子表示数n的相反数.
解:(1)现价是每千克0.8p元;
(2)去年的产量是mn件;
(3)由长方体的体积=长×宽×高,得这个长方体包装盒的体积是a a h cm3,即a2h cm3;
(4)数n的相反数是-n.
典例精析
例2 (1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
顺水速度=静水速度+水流速度
逆水速度=静水速度-水流速度
解:船在这条河中顺水行驶的速度是(v+2.5)km/h,
提示:带单位时,适当加括号
分析:
典例精析
例2 (2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,用式子表示买3个篮球、5个排球、2个足球共需要的钱数;
分析:总钱数= 3个篮球的钱数+5个排球的钱数+ 2个足球的钱数.总价=单价×数量
解:买3个篮球、5个排球、2个足球共需要(3x+5y+2z) 元.
典例精析
例2 (3)如下图(图中长度单位:cm),用式子表示三角尺的面积;
分析:三角尺的面积=三角形的面积-圆的面积
三角形的面积= 底×高
圆的面积=
解:三角尺的面积是
典例精析
例2 (4)下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
分析:住宅的建筑面积=4个长方形面积的和.
长方形面积=长×宽
解:这所住宅的建筑面积是x2+2x+18.
2x
x2
12
6
典例精析
观察式子100t,0.8p,mn,a2h,-n,都有哪些特点?
100t
0.8p
a2h
mn
-n
数
字母
相乘
相乘
数
字母
相乘
字母
字母
你发现这些式子有什么共同特点?
这些式子都是数或字母的积,像这样的式子叫做单项式.单独的一个数或一个字母也是单项式.
互动新授
单项式中的数字因数叫做这个单项式的系数.
例如,单项式100t,a2h,-n的系数分别是100,1,-1.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
例如,在单项式100t中字母t的指数是1,100t的次数是1.
那么单项式a2h的次数是多少呢?
字母a与h的指数的和是3,a2h的次数是3.
互动新授
例3 用单项式填空,并指出它们的系数和次数:
(1) 每包书有12册,n包书有______册;
(2) 底边长为acm,高为hcm的三角形的面积是_____ cm2;
(3) 棱长为acm的正方体的体积是____cm3 ;
12n
a3
解:(1)系数是12,次数是1.
(2)系数是 ,次数是2.
(3)系数是1,次数是3.
典例精析
例3 用单项式填空,并指出它们的系数和次数:
(4)一台电视机原价 b 元,现按原价的9折出售,这台电视机现在的售价是_____元;
(5)一个长方形的长是0.9 m,宽是b m ,这个长方形的面积是_____m2.
0.9b
解:(4)系数是0.9,次数是1.
0.9b
(5)系数是0.9,次数是1.
典例精析
小试牛刀
1.在括号里填上适当的式子.
(1)小明的体重38千克,小红比小明重a千克,小红的体重是( )千克.
(2)乐乐有20元钱,买文具用去了a元,还剩下( )元.
(3)每千克苹果y元,买3千克苹果需要( )元.
(4)把x个玩具分给b个小朋友,每个小朋友分得玩具( )个.
(5)地球的直径是m万千米,太阳的直径是地球直径的109倍,太阳的直径是( )万千米.
38+a
20-a
3y
109m
2.用代数式填空
⑵我国去年一户农民平均收入为n万元,今年比去年增长了30﹪,今年收入为______ 万元.
⑴长方形的面积为S,宽为a,则其长为_____.
⑶一圆形花坛半径为r,则其面积为______ .
⑷规定向东为正方向,小明向东走了b米,花花向西走的路程是小明的2y倍,则花花走了______米.
⑸体重由m千克减了4千克之后是_______千克.
1.3n
-2by
(m-4)
小试牛刀
1.下面各题的判断是否正确。
①-2xy2的系数是2; ( )
②m4y3与-x3没有系数 ; ( )
③-ab2c3的次数是0+2+3; ( )
④-a5的系数是-1; ( )
⑤ πr2h的系数是 。 ( )
⑥-2nx2y2的系数是-2n,次数为4. ( )
×
×
×
×
√
×
课堂检测
课堂检测
②③⑥
四次
四次
六次
3ab3
-3
-2
6
课堂检测
拓展训练
D
拓展训练
2.已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2﹣3ab的值.
解:因为x2y|a|+(b+2)是关于x,y的五次单项式,
所以b+2=0,2+|a|=5
所以a=±3,b=-2
则当a=﹣3,b=﹣2时,a2﹣3ab=9﹣18=﹣9;
当a=3,b=﹣2时,a2﹣3ab=9+18=27.
这些式子都是数或字母的积,像这样的式子叫做单项式.单独的一个数或一个字母也是单项式.
单项式:
单项式中的数字因数叫做这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
系数:
单项式的次数:
课堂小结
课后作业
B
A
3.电影院里座位的总排数是m,若第一排的座位数是a,并且后一排总比前一排的座位数多1个,则电影院里第m排有多少个座位?
解:因为共有m排座位,且后一排总比前一排的座位数多1个
所以第一排有a个座位,
第二排有(a+1)个座位,
第三排有(a+2)个座位,…
第m排有(a+m-1)个座位.
课后作业
谢谢聆听
