2.5等腰三角形的轴对称性(第1课时) 课件(38张PPT)
文档属性
| 名称 | 2.5等腰三角形的轴对称性(第1课时) 课件(38张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 08:54:23 | ||
图片预览


文档简介
(共38张PPT)
第2章 · 轴对称图形
2.5 等腰三角形的轴对称性
第1课时 等腰三角形及其性质
学习目标
1. 探索并证明等腰三角形的性质定理;
2.能用等腰三角形性质定理进行计算或说理;
3. 会利用基本作图作三角形:已知底边及底边上的高作等腰三角形.
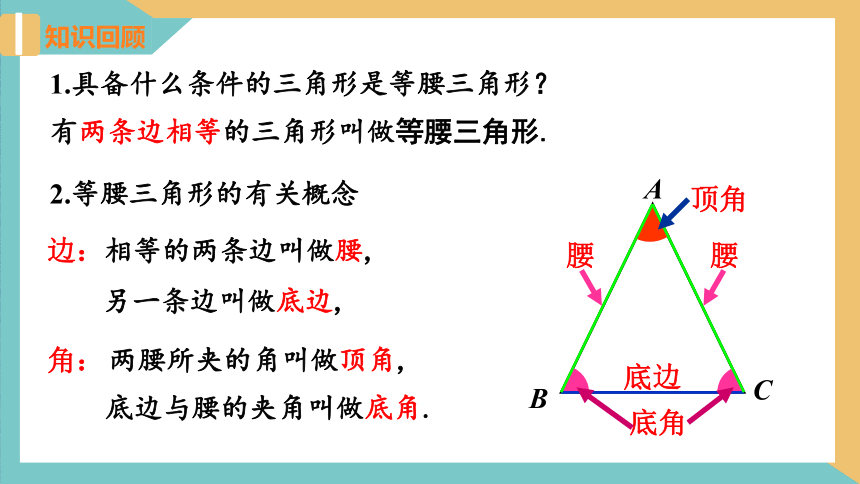
知识回顾
有两条边相等的三角形叫做等腰三角形.
1.具备什么条件的三角形是等腰三角形?
2.等腰三角形的有关概念
A
B
C
相等的两条边叫做腰,
另一条边叫做底边,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
边:
角:
探索与思考
问题1 等腰三角形是轴对称图形吗?如果是,它的对称轴是什么?
活动一 探究等腰三角形的轴对称性
分组讨论,交流结果.
A
B
C
B
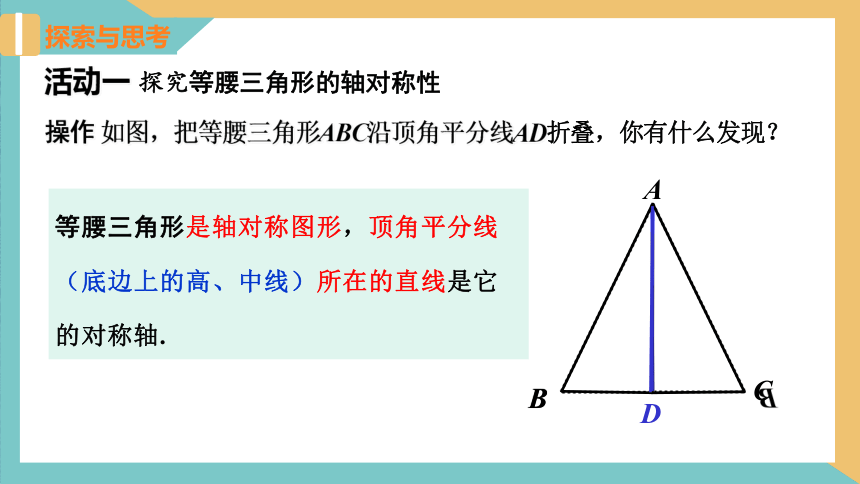
探索与思考
操作 如图,把等腰三角形ABC沿顶角平分线AD折叠,你有什么发现?
活动一 探究等腰三角形的轴对称性
A
C
D
等腰三角形是轴对称图形,顶角平分线(底边上的高、中线)所在的直线是它的对称轴.
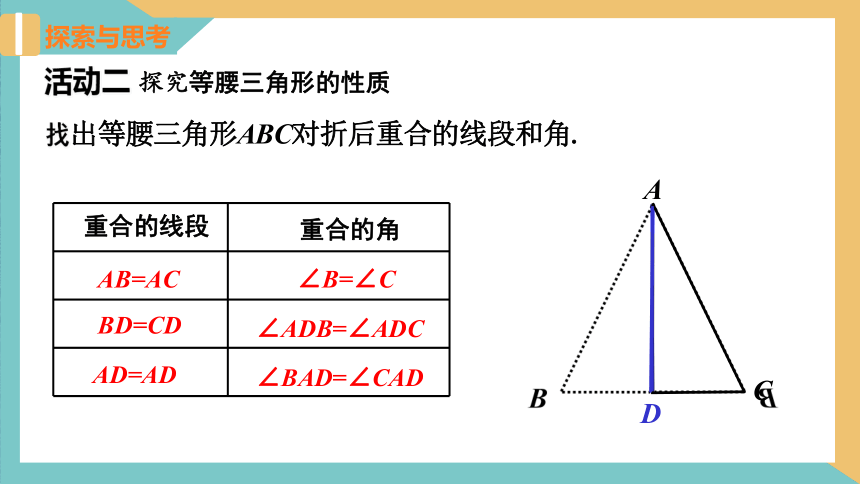
探索与思考
A
C
D
找出等腰三角形ABC对折后重合的线段和角.
活动二 探究等腰三角形的性质
探索与思考
A
C
D
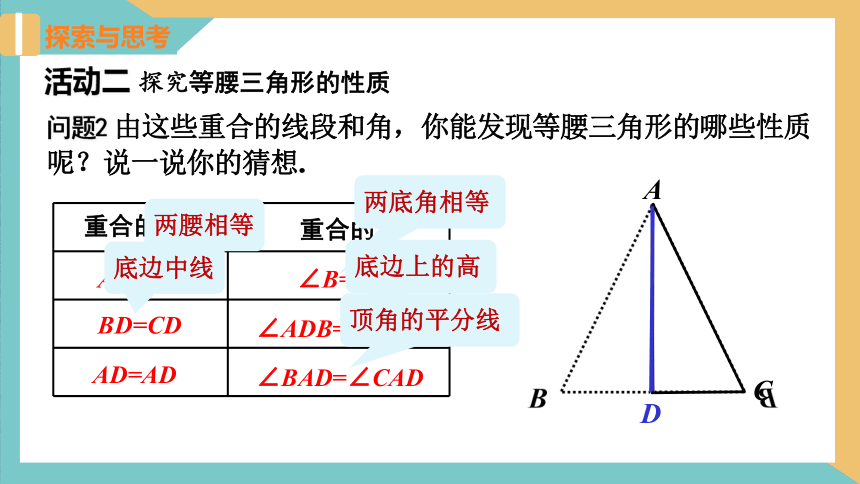
活动二 探究等腰三角形的性质
问题2 由这些重合的线段和角,你能发现等腰三角形的哪些性质呢?说一说你的猜想.
两腰相等
两底角相等
底边中线
底边上的高
顶角的平分线
探索与思考
A
C
D
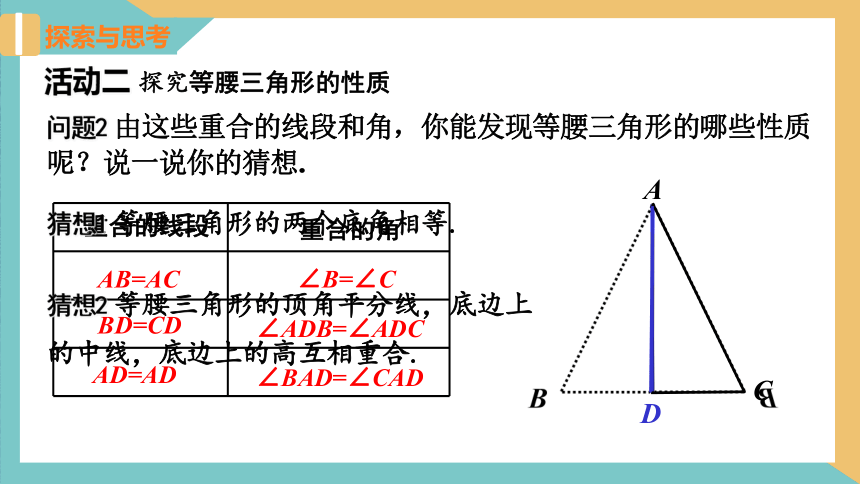
问题2 由这些重合的线段和角,你能发现等腰三角形的哪些性质呢?说一说你的猜想.
活动二 探究等腰三角形的性质
猜想1 等腰三角形的两个底角相等.
猜想2 等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.
探索与思考
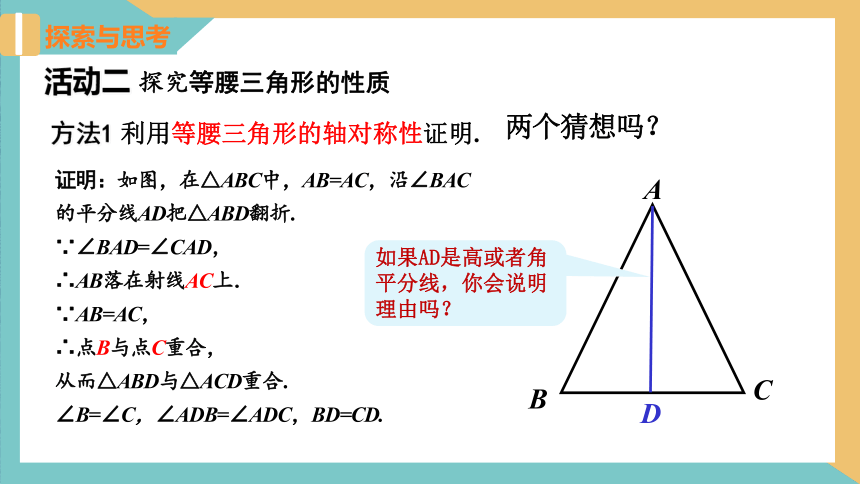
问题3 你能用我们学过的知识来证明这两个猜想吗?
活动二 探究等腰三角形的性质
方法1 利用等腰三角形的轴对称性证明.
证明:如图,在△ABC中,AB=AC,沿∠BAC的平分线AD把△ABD翻折.
∵∠BAD=∠CAD,
∴AB落在射线AC上.
∵AB=AC,
∴点B与点C重合,
从而△ABD与△ACD重合.
∠B=∠C,∠ADB=∠ADC,BD=CD.
A
B
C
D
如果AD是高或者角平分线,你会说明理由吗?
探索与思考
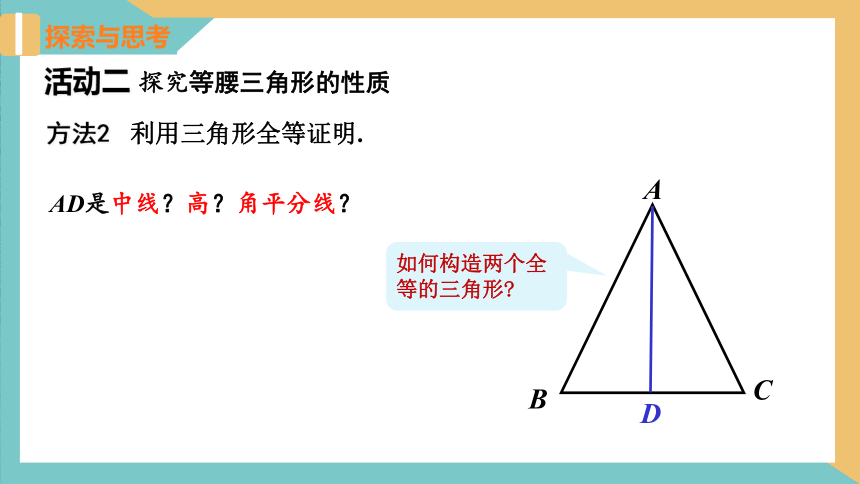
活动二 探究等腰三角形的性质
方法2 利用三角形全等证明.
A
B
C
如何构造两个全等的三角形
D
探索与思考
活动二 探究等腰三角形的性质
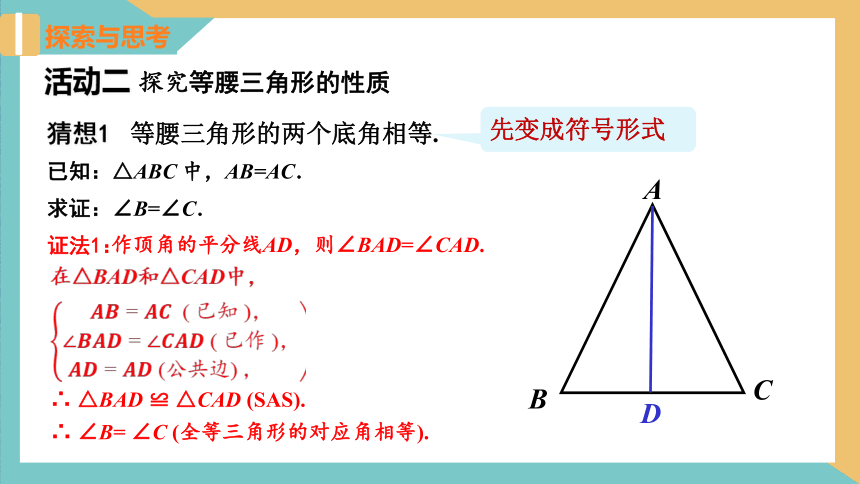
猜想1 等腰三角形的两个底角相等.
A
B
C
D
先变成符号形式
证法1:
作顶角的平分线AD,则∠BAD=∠CAD.
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等).
探索与思考
活动二 探究等腰三角形的性质
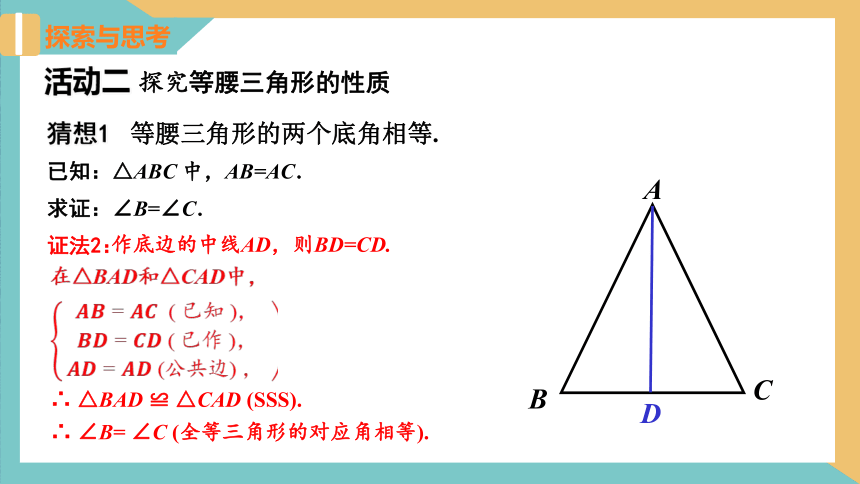
猜想1 等腰三角形的两个底角相等.
A
B
C
D
证法2:
作底边的中线AD,则BD=CD.
∴ △BAD ≌ △CAD (SSS).
∴ ∠B= ∠C (全等三角形的对应角相等).
探索与思考
活动二 探究等腰三角形的性质
猜想1 等腰三角形的两个底角相等.
A
B
C
D
证法3:
作底边的高线AD,则∠ADB=∠ADC=90°
在Rt△BAD和Rt△CAD中,
∴ Rt△BAD ≌ Rt△CAD (HL).
∴ ∠B= ∠C (全等三角形的对应角相等).
新知归纳
等腰三角形的性质定理1:
在△ABC中,
∵AC = AB (已知),
∴∠B =∠C ( 等边对等角).
符号语言:
注意:
在同一个三角形中,等边对等角.
等腰三角形的两个底角相等.
A
B
C
(简称“等边对等角”)
猜想2 等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.
探索与思考
活动二 探究等腰三角形的性质
证明:∵△BAD≌ △CAD,
∴BD=CD,∠ADB=∠ADC,∠BAD=∠CAD.
又∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC= 90° ,
即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线 .
A
B
C
D
等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合.
新知归纳
等腰三角形的性质定理2:
A
B
C
(简称“三线合一”)
D
1
2
∵AB=AC, ∠1=∠2 (已知),
∴BD=CD,AD⊥BC (等腰三角形三线合一).
∵AB=AC, BD=CD (已知),
∴∠1=∠2,AD⊥BC (等腰三角形三线合一).
∵AB=AC, AD⊥BC (已知),
∴BD=CD,∠1=∠2 (等腰三角形三线合一).
如图,在△ABC中,
A
B
C
探索与思考
问题4 作出等腰三角形腰上的中线、角平分线、高,它们重合吗?
活动二 探究等腰三角形的性质
D
F
E
新知巩固
1.判断下列语句是否正确.
(1)等腰三角形的角平分线、中线和高互相重合.( )
(2)等腰三角形一角的平分线,一边上的中线,一边上的高
都是它的对称轴 ( )
(3)等腰三角形的两角相等.( )
(4)等腰三角形的顶角平分线一定垂直底边.( )
×
×
×
√
2. 在△ABC中,AB=AC,点D在BC上.
如果∠BAD=∠CAD,那么 AD⊥BC ,BD=CD;
如果BD=CD,那么∠______=∠_______, _______⊥______;
如果AD⊥BC,那么_________________,_________.
新知巩固
BAD
CAD
AD
BC
A
B
C
D
∠BAD=∠CAD
BD=CD
新知巩固
3. 如图,在△ABC中,AB=AC,
(1)如果∠B=70°,那么∠C=____,∠A=____.
A
B
C
D
70°
40°
(2)如果∠A=70°,那么∠B=____,∠C= ___.
(3)如果有一个角等于120°,
那么∠A= ____ ,∠B=___ ,∠C =___ .
(4)如果有一个角等于50°,那么另两个角等于多少度?
55°
55°
120°
30°
30°
解:若∠A=50°,则∠B=∠C=65°;
若∠B=∠C=50°,则∠A=80°.
已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.
探索与思考
1.作线段BC=a.
2.作线段BC的垂直平分线MN,MN交BC于点D.
3.在MN上截取线段DA,使AD=h.
4.连接AB、AC.
△ABC就是所求作的等腰三角形.
活动三 用直尺和圆规作等腰三角形
操作 用直尺和圆规作等腰三角形ABC,使底边BC=a,高AD=h.
a
h
a
M
N
●
A
B
●
●
C
h
●
D
作法:
新知归纳
文字语言 图形语言 符号语言
等边对等角
底边上的高、中线及顶角平分线重合
A
B
C
A
B
C
D
在△ABC中,
∵AC = AB (已知),
∴∠B =∠C ( 等边对等角).
在△ABC中,AB=AC.
(1)∵∠BAD=∠CAD,∴BD=CD,AD⊥BC;
(2)∵AD⊥BC,∴BD=CD,∠BAD=∠CAD;
(3)∵BD=CD,∴∠BAD=∠CAD,AD⊥BC.
例题讲解
例1 已知:如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
求证: ∠ADB=∠BAC.
A
B
C
D
要证∠ADB=∠BAC
只要找与∠1相等且与∠C也相等的角.
由于∠BAC=∠1+∠2,
∠ADB=∠C+∠2.
只要证∠1=∠C
1
2
?
?
例题讲解
例1 已知:如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
求证: ∠ADB=∠BAC.
A
B
C
D
1
2
?
?
证明:∵AB=AC,AD=BD,
∴∠B=∠C,∠B=∠1(等边对等角)
∴∠C=∠1.
∵∠ADB是△ADC的外角,
∴∠ADB=∠C+∠2.
∴∠ADB=∠1+∠2=∠BAC.
例题讲解
例2 已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF.
D
A
B
C
F
E
要证DE=DF
已知AB=AC
已知DE⊥AB, DF⊥AC
D是BC的中点
只要证∠B=∠C
只要证△DBE≌△DCF
方法一:
例题讲解
例2 已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF.
D
A
B
C
F
E
证明:
∵AB=AC,
∴ ∠B= ∠C (等边对等角).
∵D是BC的中点,
∴ DB=DC .
∵DE⊥AB,DF⊥AC,
∴ ∠DEB=∠DFC=90°.
∴ △DBE ≌ △DCF(AAS).
∴ DE=DF .
例题讲解
例2 已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF.
D
A
B
C
F
E
要证DE=DF
已知AB=AC,D是BC的中点
已知DE⊥AB, DF⊥AC
只要证AD平分∠BAC
方法二:连接AD.
例题讲解
例2 已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF .
D
A
B
C
F
E
证明:∵ AB=AC,D是BC的中点,
∴ AD平分∠BAC(三线合一).
∵ DE⊥AB,DF⊥AC,
∴ DE=DF.
新知巩固
1. 如图,在△ABC中,点D在BC上,AD=BD,AB=AC=CD.
找出图中相等的角并说明理由.
解:∠BAD=∠B=∠C;∠BAC=∠ADB;∠ADC=∠DAC.
∵AD=BD,
∴∠BAD=∠B.
∵AB=AC,
∴∠C=∠B.
∴∠BAD=∠B=∠C
A
B
C
D
∵DC=AC,
∴∠DAC=∠ADC.
∵∠ADB=∠C+∠DAC,
∠BAC=∠BAD+∠DAC,
∴∠ADB=∠BAC.
新知巩固
2.如图的房屋人字梁架中,AB=AC ,BD=DC, ∠BAC=110°,
(1) 求∠B、∠C、∠1、∠2的度数;
(2) 求证:AD⊥BC .
(2) 证明:∵AB=AC,BD=DC(已知)
∴ AD⊥BC(三线合一)
1
2
课堂小结
等腰三角形的性质
等边对等角
三线合一
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.
常用辅助线:作顶角平分线、底边上的高、底边上的中线是常见的辅助线
当堂检测
2.如图,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是 ( )
A. ∠B=∠C B. AD⊥BC
C. AD平分∠BAC D. AB=2BD
A
B
C
D
D
1.等腰三角形的对称轴是 ( )
A.底边上的中线 B.顶角的平分线
C.底边上的高 D.底边的垂直平分线
D
当堂检测
A
B
C
D
E
F
当堂检测
4.(1)等腰三角形一个底角为75°,它的另外两个角为____ ________;
(2)等腰三角形一个角为36°,它的另外两个角为____________________;
(3)等腰三角形一个角为120°,它的另外两个角为_ ___ _______ __.
75°, 30°
72°,72°或36°,108°
30°,30°
5. 在△ABC中, AB=AC,AB的垂直平分线与AC所在的直线相交得的锐角为50°,则底角的大小为___________.
70°或20°
A
B
C
A
B
C
注意:当题目未给定三角形的形状时,一般需分锐角三角形和钝角三角形两种情况进行讨论.
当堂检测
6.如图,AOB是一钢架,且∠AOB=10°,为使钢架更加坚固,需在其内部添一些钢管EF、FM、MH……,添加的 钢管长度都与OE相等,添加这样的钢管4根时,则∠AHB 的度数为__________.
E
O
F
H
M
B
A
10°
50°
当堂检测
7.如图,在△ABC中,点D在BC上,AD=BD,AB=AC=CD.
求∠BAC的度数.
解:设∠B=x°.
∵AD=BD,
∴∠BAD=∠B=x°.
∴∠ADC=∠BAD+∠B=(2x)°.
∵DC=AC,
∴∠DAC=∠ADC=(2x)°.
∵AB=AC,
∴∠C=∠B=x°.
∵∠C+∠DAC+∠ADC=180°,
∴x+2x+2x=180.
∴x=36,即∠B=36°.
∴∠BAC=180°-36°-36°=108°
A
B
C
D
当堂检测
8. 已知点D、E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
A
C
B
E
D
图①
G
(1)证明:如图①,过A作AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE.
当堂检测
8. 已知点D、E在△ABC的边BC上,AB=AC.
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
A
F
C
B
E
D
图②
(2)证明:∵F为DE的中点,
∴DF=EF.
∵BD=CE,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,
∴AF⊥BC.
第2章 · 轴对称图形
2.5 等腰三角形的轴对称性
第1课时 等腰三角形及其性质
学习目标
1. 探索并证明等腰三角形的性质定理;
2.能用等腰三角形性质定理进行计算或说理;
3. 会利用基本作图作三角形:已知底边及底边上的高作等腰三角形.
知识回顾
有两条边相等的三角形叫做等腰三角形.
1.具备什么条件的三角形是等腰三角形?
2.等腰三角形的有关概念
A
B
C
相等的两条边叫做腰,
另一条边叫做底边,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
边:
角:
探索与思考
问题1 等腰三角形是轴对称图形吗?如果是,它的对称轴是什么?
活动一 探究等腰三角形的轴对称性
分组讨论,交流结果.
A
B
C
B
探索与思考
操作 如图,把等腰三角形ABC沿顶角平分线AD折叠,你有什么发现?
活动一 探究等腰三角形的轴对称性
A
C
D
等腰三角形是轴对称图形,顶角平分线(底边上的高、中线)所在的直线是它的对称轴.
探索与思考
A
C
D
找出等腰三角形ABC对折后重合的线段和角.
活动二 探究等腰三角形的性质
探索与思考
A
C
D
活动二 探究等腰三角形的性质
问题2 由这些重合的线段和角,你能发现等腰三角形的哪些性质呢?说一说你的猜想.
两腰相等
两底角相等
底边中线
底边上的高
顶角的平分线
探索与思考
A
C
D
问题2 由这些重合的线段和角,你能发现等腰三角形的哪些性质呢?说一说你的猜想.
活动二 探究等腰三角形的性质
猜想1 等腰三角形的两个底角相等.
猜想2 等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.
探索与思考
问题3 你能用我们学过的知识来证明这两个猜想吗?
活动二 探究等腰三角形的性质
方法1 利用等腰三角形的轴对称性证明.
证明:如图,在△ABC中,AB=AC,沿∠BAC的平分线AD把△ABD翻折.
∵∠BAD=∠CAD,
∴AB落在射线AC上.
∵AB=AC,
∴点B与点C重合,
从而△ABD与△ACD重合.
∠B=∠C,∠ADB=∠ADC,BD=CD.
A
B
C
D
如果AD是高或者角平分线,你会说明理由吗?
探索与思考
活动二 探究等腰三角形的性质
方法2 利用三角形全等证明.
A
B
C
如何构造两个全等的三角形
D
探索与思考
活动二 探究等腰三角形的性质
猜想1 等腰三角形的两个底角相等.
A
B
C
D
先变成符号形式
证法1:
作顶角的平分线AD,则∠BAD=∠CAD.
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等).
探索与思考
活动二 探究等腰三角形的性质
猜想1 等腰三角形的两个底角相等.
A
B
C
D
证法2:
作底边的中线AD,则BD=CD.
∴ △BAD ≌ △CAD (SSS).
∴ ∠B= ∠C (全等三角形的对应角相等).
探索与思考
活动二 探究等腰三角形的性质
猜想1 等腰三角形的两个底角相等.
A
B
C
D
证法3:
作底边的高线AD,则∠ADB=∠ADC=90°
在Rt△BAD和Rt△CAD中,
∴ Rt△BAD ≌ Rt△CAD (HL).
∴ ∠B= ∠C (全等三角形的对应角相等).
新知归纳
等腰三角形的性质定理1:
在△ABC中,
∵AC = AB (已知),
∴∠B =∠C ( 等边对等角).
符号语言:
注意:
在同一个三角形中,等边对等角.
等腰三角形的两个底角相等.
A
B
C
(简称“等边对等角”)
猜想2 等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.
探索与思考
活动二 探究等腰三角形的性质
证明:∵△BAD≌ △CAD,
∴BD=CD,∠ADB=∠ADC,∠BAD=∠CAD.
又∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC= 90° ,
即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线 .
A
B
C
D
等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合.
新知归纳
等腰三角形的性质定理2:
A
B
C
(简称“三线合一”)
D
1
2
∵AB=AC, ∠1=∠2 (已知),
∴BD=CD,AD⊥BC (等腰三角形三线合一).
∵AB=AC, BD=CD (已知),
∴∠1=∠2,AD⊥BC (等腰三角形三线合一).
∵AB=AC, AD⊥BC (已知),
∴BD=CD,∠1=∠2 (等腰三角形三线合一).
如图,在△ABC中,
A
B
C
探索与思考
问题4 作出等腰三角形腰上的中线、角平分线、高,它们重合吗?
活动二 探究等腰三角形的性质
D
F
E
新知巩固
1.判断下列语句是否正确.
(1)等腰三角形的角平分线、中线和高互相重合.( )
(2)等腰三角形一角的平分线,一边上的中线,一边上的高
都是它的对称轴 ( )
(3)等腰三角形的两角相等.( )
(4)等腰三角形的顶角平分线一定垂直底边.( )
×
×
×
√
2. 在△ABC中,AB=AC,点D在BC上.
如果∠BAD=∠CAD,那么 AD⊥BC ,BD=CD;
如果BD=CD,那么∠______=∠_______, _______⊥______;
如果AD⊥BC,那么_________________,_________.
新知巩固
BAD
CAD
AD
BC
A
B
C
D
∠BAD=∠CAD
BD=CD
新知巩固
3. 如图,在△ABC中,AB=AC,
(1)如果∠B=70°,那么∠C=____,∠A=____.
A
B
C
D
70°
40°
(2)如果∠A=70°,那么∠B=____,∠C= ___.
(3)如果有一个角等于120°,
那么∠A= ____ ,∠B=___ ,∠C =___ .
(4)如果有一个角等于50°,那么另两个角等于多少度?
55°
55°
120°
30°
30°
解:若∠A=50°,则∠B=∠C=65°;
若∠B=∠C=50°,则∠A=80°.
已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.
探索与思考
1.作线段BC=a.
2.作线段BC的垂直平分线MN,MN交BC于点D.
3.在MN上截取线段DA,使AD=h.
4.连接AB、AC.
△ABC就是所求作的等腰三角形.
活动三 用直尺和圆规作等腰三角形
操作 用直尺和圆规作等腰三角形ABC,使底边BC=a,高AD=h.
a
h
a
M
N
●
A
B
●
●
C
h
●
D
作法:
新知归纳
文字语言 图形语言 符号语言
等边对等角
底边上的高、中线及顶角平分线重合
A
B
C
A
B
C
D
在△ABC中,
∵AC = AB (已知),
∴∠B =∠C ( 等边对等角).
在△ABC中,AB=AC.
(1)∵∠BAD=∠CAD,∴BD=CD,AD⊥BC;
(2)∵AD⊥BC,∴BD=CD,∠BAD=∠CAD;
(3)∵BD=CD,∴∠BAD=∠CAD,AD⊥BC.
例题讲解
例1 已知:如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
求证: ∠ADB=∠BAC.
A
B
C
D
要证∠ADB=∠BAC
只要找与∠1相等且与∠C也相等的角.
由于∠BAC=∠1+∠2,
∠ADB=∠C+∠2.
只要证∠1=∠C
1
2
?
?
例题讲解
例1 已知:如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
求证: ∠ADB=∠BAC.
A
B
C
D
1
2
?
?
证明:∵AB=AC,AD=BD,
∴∠B=∠C,∠B=∠1(等边对等角)
∴∠C=∠1.
∵∠ADB是△ADC的外角,
∴∠ADB=∠C+∠2.
∴∠ADB=∠1+∠2=∠BAC.
例题讲解
例2 已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF.
D
A
B
C
F
E
要证DE=DF
已知AB=AC
已知DE⊥AB, DF⊥AC
D是BC的中点
只要证∠B=∠C
只要证△DBE≌△DCF
方法一:
例题讲解
例2 已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF.
D
A
B
C
F
E
证明:
∵AB=AC,
∴ ∠B= ∠C (等边对等角).
∵D是BC的中点,
∴ DB=DC .
∵DE⊥AB,DF⊥AC,
∴ ∠DEB=∠DFC=90°.
∴ △DBE ≌ △DCF(AAS).
∴ DE=DF .
例题讲解
例2 已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF.
D
A
B
C
F
E
要证DE=DF
已知AB=AC,D是BC的中点
已知DE⊥AB, DF⊥AC
只要证AD平分∠BAC
方法二:连接AD.
例题讲解
例2 已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF .
D
A
B
C
F
E
证明:∵ AB=AC,D是BC的中点,
∴ AD平分∠BAC(三线合一).
∵ DE⊥AB,DF⊥AC,
∴ DE=DF.
新知巩固
1. 如图,在△ABC中,点D在BC上,AD=BD,AB=AC=CD.
找出图中相等的角并说明理由.
解:∠BAD=∠B=∠C;∠BAC=∠ADB;∠ADC=∠DAC.
∵AD=BD,
∴∠BAD=∠B.
∵AB=AC,
∴∠C=∠B.
∴∠BAD=∠B=∠C
A
B
C
D
∵DC=AC,
∴∠DAC=∠ADC.
∵∠ADB=∠C+∠DAC,
∠BAC=∠BAD+∠DAC,
∴∠ADB=∠BAC.
新知巩固
2.如图的房屋人字梁架中,AB=AC ,BD=DC, ∠BAC=110°,
(1) 求∠B、∠C、∠1、∠2的度数;
(2) 求证:AD⊥BC .
(2) 证明:∵AB=AC,BD=DC(已知)
∴ AD⊥BC(三线合一)
1
2
课堂小结
等腰三角形的性质
等边对等角
三线合一
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.
常用辅助线:作顶角平分线、底边上的高、底边上的中线是常见的辅助线
当堂检测
2.如图,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是 ( )
A. ∠B=∠C B. AD⊥BC
C. AD平分∠BAC D. AB=2BD
A
B
C
D
D
1.等腰三角形的对称轴是 ( )
A.底边上的中线 B.顶角的平分线
C.底边上的高 D.底边的垂直平分线
D
当堂检测
A
B
C
D
E
F
当堂检测
4.(1)等腰三角形一个底角为75°,它的另外两个角为____ ________;
(2)等腰三角形一个角为36°,它的另外两个角为____________________;
(3)等腰三角形一个角为120°,它的另外两个角为_ ___ _______ __.
75°, 30°
72°,72°或36°,108°
30°,30°
5. 在△ABC中, AB=AC,AB的垂直平分线与AC所在的直线相交得的锐角为50°,则底角的大小为___________.
70°或20°
A
B
C
A
B
C
注意:当题目未给定三角形的形状时,一般需分锐角三角形和钝角三角形两种情况进行讨论.
当堂检测
6.如图,AOB是一钢架,且∠AOB=10°,为使钢架更加坚固,需在其内部添一些钢管EF、FM、MH……,添加的 钢管长度都与OE相等,添加这样的钢管4根时,则∠AHB 的度数为__________.
E
O
F
H
M
B
A
10°
50°
当堂检测
7.如图,在△ABC中,点D在BC上,AD=BD,AB=AC=CD.
求∠BAC的度数.
解:设∠B=x°.
∵AD=BD,
∴∠BAD=∠B=x°.
∴∠ADC=∠BAD+∠B=(2x)°.
∵DC=AC,
∴∠DAC=∠ADC=(2x)°.
∵AB=AC,
∴∠C=∠B=x°.
∵∠C+∠DAC+∠ADC=180°,
∴x+2x+2x=180.
∴x=36,即∠B=36°.
∴∠BAC=180°-36°-36°=108°
A
B
C
D
当堂检测
8. 已知点D、E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
A
C
B
E
D
图①
G
(1)证明:如图①,过A作AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE.
当堂检测
8. 已知点D、E在△ABC的边BC上,AB=AC.
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
A
F
C
B
E
D
图②
(2)证明:∵F为DE的中点,
∴DF=EF.
∵BD=CE,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,
∴AF⊥BC.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
