23.3 课题学习 图案设计 课件(21张PPT)
文档属性
| 名称 | 23.3 课题学习 图案设计 课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 09:01:41 | ||
图片预览







文档简介
(共21张PPT)
1 学会利用旋转、轴对称或平移进行简单的图案设计.
2 了解和欣赏平移、旋转在现实生活中的应用.
3 灵活运用平移与旋转组合的方式进行一些图案设计.
复习巩固
探究新知
新知讲解
典例分析
针对训练
归纳小结
探究新知
新知讲解
典例分析
针对训练
布置作业
【提问1】简述平移、轴对称、旋转的概念?
在平面内,将一个图形沿某个方向移动一定的距离。
两个图形如果沿着某条直线对折,直线两旁的部分能够互相重合,则这两个图形关于这条直线轴对称。
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
平移的概念:
轴对称概念:
旋转的概念:
【提问2】平移、轴对称变换、旋转有什么共同特征?
平移、轴对称和旋转都不改变图形的形状、大小,只改变图形的位置,它们都是全等变换.
[问题1]生活中有很多由几何图形组成的优美图案,你知道它们是怎样形成的吗?
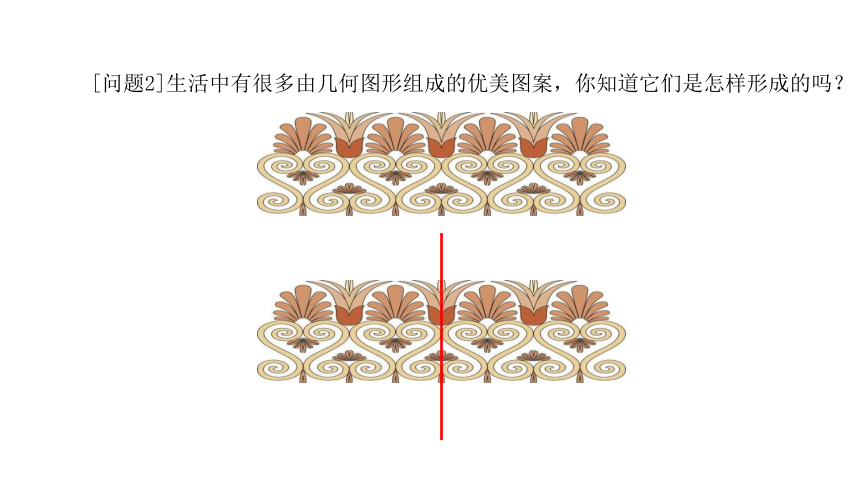
[问题2]生活中有很多由几何图形组成的优美图案,你知道它们是怎样形成的吗?
[问题3]观察下面的图案,分析它是将哪种基本图形经过哪些变换得到的?
基本图案
图案形成过程图案
[问题4]观察下面的图案,分析它是将哪种基本图形经过哪些变换得到的?
将 经过旋转、轴对称和平移得到的.
[问题5]简述分析图案形成过程的方法?
1)找出组成原图案最基本的图形;
2)说明将该基本图形运用平移、旋转、轴对称中的哪些图形变换,通过怎样的变换方式得到原图案.
解:1)是由基本图形 旋转十次后得到的;
2)是由基本图形 平移两次后得到的;
3)是由基本图形 旋转五次后得到的;
4)是由基本图形 旋转五次后得到的.
(答案不唯一)
例1 分析下列图案的形成过程.
1.下面四个图案中,不能由基本图案旋转得到的是( )
【详解】A、可由一个基本“花瓣”绕其中心经过7次旋转,每次旋转45°得到;
B、可由一个基本“菱形”绕其中心经过5次旋转,每次旋转60°得到;
C、可由一个基本”直角三角形”绕其中心绕其中心经过5次旋转,每次旋转60°得到;
D、不能由基本图案旋转得到.
故选D.
仔细观察图案的情况,分析构成的基本图形,再分析图形变换的过程和方式:是通过平移、轴对称、旋转中的一种变换还是其中的几种变换的组合.另外要注意图形形成方式不是唯一的,基本图形也不唯一,在分析时,要全面思考,认真分析.
【小组讨论】请以给定的图形○○△△=(两个圆,两个三角形,两条平行线)为构件,尽可能多地构思有意义的一些图形,并写上一两句贴切,诙谐的解说词.如下图就是符合要求的图形,你能构思其它图形吗 比一比,看谁想得多,看谁想得妙!(图形不限定大小,线段不限定长短,每小组至少给出5个答案,比一比哪个小组画的最漂亮)
鱼翔浅底
小猪小猪胖乎乎
示例
[问题]简述设计图案的方法?
图案的设计通常是利用基本图形通过轴对称、平移、旋转这三种基本形式变换来进行的,三种基本变换都有一个共同特征,那就是变换前后图形的形状、大小不发生变化,只有位置发生了变化,它们都属于全等变换。利用平移,旋转,轴对称中的一种或几种组合,就能把一个简单的图形设计成一个美丽的图案。
例2 填空
1.图案 可以通过将字母________经过______变换得到.
2.图案 可以通过将________经过______变换得到.
3.图案 可以看做将汉字________经过________变换得到.
4.图案 可以视为利用图形的______设计而成的,也可以视为利用图形的______设计而成的.
旋转
正方形
平移
弓
轴对称
S
旋转
轴对称
1. 某公司为节约开支,购买了同种质量、两种不同颜色的残缺地板砖,准备用来装饰地面。现已经把它们加工成如图1(a)所示的等腰直角三角形,李兵同学设计出图1中(b)(c)(d)(e)四种图案.
1)请问你喜欢其中的哪个图案,并简述该图案的形成过程;
2)请你利用平移、旋转或轴对称等变换,再设计一幅与上述不同的图案.
2 如图,有一个4×4的正方形网格,网格中每个小正方形的边长为1.请你以左上角的三角形为基本图形,通过平移、轴对称或旋转,在网格中设计一个图案,使其既是轴对称图形,又是以点O为对称中心的中心对称图形.所作图案用阴影标识,且图案的面积为4(即阴影部分面积为4).
O
3 某单位搞绿化,要在一块圆形空地上种植四种颜色的花,为了便于管理和美观,相同颜色的花集中种植,且每种颜色的花所占的面积相同,现征集设计方案,你能帮忙设计吗?
答案不唯一
4 如图,下列4×4网格图是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(2)在下图中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
1 学会利用旋转、轴对称或平移进行简单的图案设计.
2 了解和欣赏平移、旋转在现实生活中的应用.
3 灵活运用平移与旋转组合的方式进行一些图案设计.
复习巩固
探究新知
新知讲解
典例分析
针对训练
归纳小结
探究新知
新知讲解
典例分析
针对训练
布置作业
【提问1】简述平移、轴对称、旋转的概念?
在平面内,将一个图形沿某个方向移动一定的距离。
两个图形如果沿着某条直线对折,直线两旁的部分能够互相重合,则这两个图形关于这条直线轴对称。
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
平移的概念:
轴对称概念:
旋转的概念:
【提问2】平移、轴对称变换、旋转有什么共同特征?
平移、轴对称和旋转都不改变图形的形状、大小,只改变图形的位置,它们都是全等变换.
[问题1]生活中有很多由几何图形组成的优美图案,你知道它们是怎样形成的吗?
[问题2]生活中有很多由几何图形组成的优美图案,你知道它们是怎样形成的吗?
[问题3]观察下面的图案,分析它是将哪种基本图形经过哪些变换得到的?
基本图案
图案形成过程图案
[问题4]观察下面的图案,分析它是将哪种基本图形经过哪些变换得到的?
将 经过旋转、轴对称和平移得到的.
[问题5]简述分析图案形成过程的方法?
1)找出组成原图案最基本的图形;
2)说明将该基本图形运用平移、旋转、轴对称中的哪些图形变换,通过怎样的变换方式得到原图案.
解:1)是由基本图形 旋转十次后得到的;
2)是由基本图形 平移两次后得到的;
3)是由基本图形 旋转五次后得到的;
4)是由基本图形 旋转五次后得到的.
(答案不唯一)
例1 分析下列图案的形成过程.
1.下面四个图案中,不能由基本图案旋转得到的是( )
【详解】A、可由一个基本“花瓣”绕其中心经过7次旋转,每次旋转45°得到;
B、可由一个基本“菱形”绕其中心经过5次旋转,每次旋转60°得到;
C、可由一个基本”直角三角形”绕其中心绕其中心经过5次旋转,每次旋转60°得到;
D、不能由基本图案旋转得到.
故选D.
仔细观察图案的情况,分析构成的基本图形,再分析图形变换的过程和方式:是通过平移、轴对称、旋转中的一种变换还是其中的几种变换的组合.另外要注意图形形成方式不是唯一的,基本图形也不唯一,在分析时,要全面思考,认真分析.
【小组讨论】请以给定的图形○○△△=(两个圆,两个三角形,两条平行线)为构件,尽可能多地构思有意义的一些图形,并写上一两句贴切,诙谐的解说词.如下图就是符合要求的图形,你能构思其它图形吗 比一比,看谁想得多,看谁想得妙!(图形不限定大小,线段不限定长短,每小组至少给出5个答案,比一比哪个小组画的最漂亮)
鱼翔浅底
小猪小猪胖乎乎
示例
[问题]简述设计图案的方法?
图案的设计通常是利用基本图形通过轴对称、平移、旋转这三种基本形式变换来进行的,三种基本变换都有一个共同特征,那就是变换前后图形的形状、大小不发生变化,只有位置发生了变化,它们都属于全等变换。利用平移,旋转,轴对称中的一种或几种组合,就能把一个简单的图形设计成一个美丽的图案。
例2 填空
1.图案 可以通过将字母________经过______变换得到.
2.图案 可以通过将________经过______变换得到.
3.图案 可以看做将汉字________经过________变换得到.
4.图案 可以视为利用图形的______设计而成的,也可以视为利用图形的______设计而成的.
旋转
正方形
平移
弓
轴对称
S
旋转
轴对称
1. 某公司为节约开支,购买了同种质量、两种不同颜色的残缺地板砖,准备用来装饰地面。现已经把它们加工成如图1(a)所示的等腰直角三角形,李兵同学设计出图1中(b)(c)(d)(e)四种图案.
1)请问你喜欢其中的哪个图案,并简述该图案的形成过程;
2)请你利用平移、旋转或轴对称等变换,再设计一幅与上述不同的图案.
2 如图,有一个4×4的正方形网格,网格中每个小正方形的边长为1.请你以左上角的三角形为基本图形,通过平移、轴对称或旋转,在网格中设计一个图案,使其既是轴对称图形,又是以点O为对称中心的中心对称图形.所作图案用阴影标识,且图案的面积为4(即阴影部分面积为4).
O
3 某单位搞绿化,要在一块圆形空地上种植四种颜色的花,为了便于管理和美观,相同颜色的花集中种植,且每种颜色的花所占的面积相同,现征集设计方案,你能帮忙设计吗?
答案不唯一
4 如图,下列4×4网格图是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(2)在下图中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
同课章节目录
