第二十三章 旋转 单元复习课件(41张PPT)
文档属性
| 名称 | 第二十三章 旋转 单元复习课件(41张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 09:32:52 | ||
图片预览










文档简介
(共41张PPT)
学习目标
1 了解图形的旋转的有关概念并理解它的基本性质;
2 了解中心对称和中心对称图形的概念并理解它的基本性质;
3 掌握关于原点对称的两点的关系并应用。
本章重点内容:
1 理解并掌握图形旋转和中心对称基本性质。
2 两个点关于原点对称时,它们坐标之间的关系。
本章难点内容:
1 图形旋转的基本性质的归纳与运用。
2 中心对称的基本性质的归纳与运用。
让学生经历观察、操作等过程,了解图形旋转的概念,探索图形旋转基本性质,进一步发展空间观察,培养运动几何的观点,增强审美意识。让学生通过独立思考,自主探究和合作交流进一步体会旋转的数学内涵,享受学习乐趣,学生运用所学知识进行图案设计活动,激发学习热情。
基础巩固(旋转)
在平面内,将一个平面图形绕着平面内一个定点沿某一方向转动一个角度,就叫做图形的旋转.这个定点叫做旋转中心.转动的角叫做旋转角.
O
[提问]如果图形上的点P经过旋转变为点P′,那么点P和P′叫做这个旋转的________.
旋转中心是_________,旋转角度是_________.
旋转方向__________.
点O
120°
P′
对应点
120°
P
顺时针
基础巩固(旋转的性质)
1.对应点到旋转中心的距离相等.
2.对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等.
基础巩固(旋转作图的一般步骤)
1)找出图形的关键点;
2)确定旋转中心,旋转方向和旋转角;
3)将关键点与旋转中心连接起来,然后按旋转方向分别将它们旋转一个角,得到关键点的对应点;
4)按照原图形的顺序连接这些对应点,所得到的图形就是旋转后的图形.
基础巩固(中心对称)
把一个图形绕某一个点旋转180 ,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称.
1)这个点叫做对称中心.
2)这两个图形中的对应点叫做关于中心的对称点.
A
B
O
C
D
[提问]
1)你能指出图中的对称点吗?
2)点C、点A、点O的位置关系怎样
3)线段AO、OC的大小关系呢
点A与点C、点B与点D
在一条直线上
相等
基础巩固(中心对称的性质)
1)中心对称的两个图形,对称点所连线段经过对称中心,而且被对称中心所平分.
2)中心对称的两个图形是全等形.
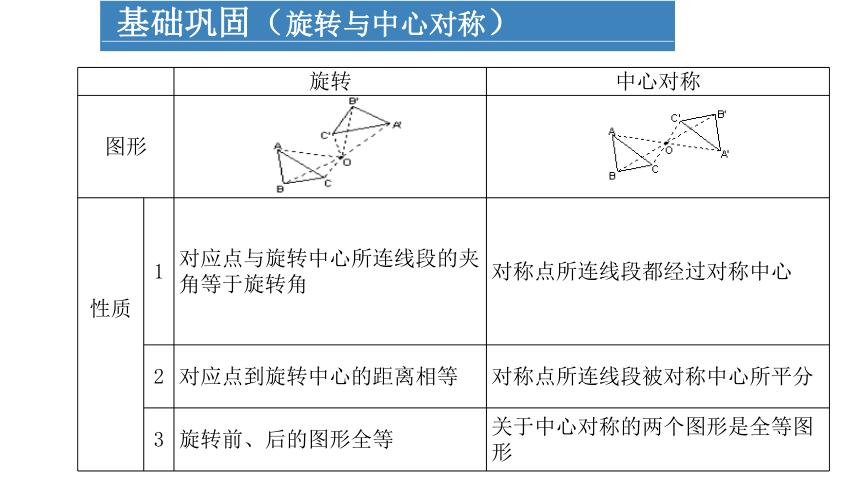
基础巩固(旋转与中心对称)
旋转 中心对称
图形
性质
1 对应点与旋转中心所连线段的夹角等于旋转角 对称点所连线段都经过对称中心
2 对应点到旋转中心的距离相等 对称点所连线段被对称中心所平分
3 旋转前、后的图形全等 关于中心对称的两个图形是全等图形
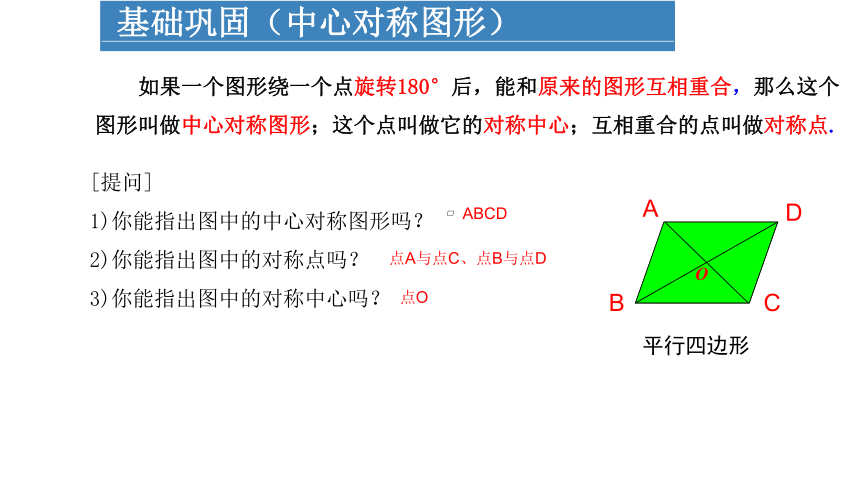
基础巩固(中心对称图形)
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
平行四边形
O
A
B
C
D
[提问]
1)你能指出图中的中心对称图形吗?
2)你能指出图中的对称点吗?
3)你能指出图中的对称中心吗?
ABCD
点O
点A与点C、点B与点D
基础巩固(中心对称与中心对称图形的区别与联系)
名称 中心对称 中心对称图形
定义 把一个图形绕着某一个点旋转180 ,如果他能够与另一个图形重合,那么就说这两个图形关于这点对称或中心对称 如果一个图形绕着一个点旋转180 后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形
性质 ①两个图形可完全重合;
②对应点连线都经过对称中心,并且被对称中心平分 ①是一个特殊的图形
②对应点连线都经过对称中心,并且被对称中心平分
区别 ①两个图形的关系
②对称点在两个图形上 ①具有某种性质的一个图形
②对称点在一个图形上
联系 若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,
若把中心对称的两个图形看作一个整体,则成为中心对称图形。
基础巩固(关于原点对称的点的坐标的关系)
两个点关于原点对称时,它们的坐标符号相反,
P(x,y)
P′ (–x,–y)
关于原点O的对称点
P(x,y)
P′ (x,–y)
关于x轴的对称点
P(x,y)
P′ (–x,y)
关于y轴的对称点
横、纵坐标都互为相反数
纵坐标相同,横坐标互为相反数
横坐标相同,纵坐标互为相反数
基础巩固(平移、轴对称、旋转的区别与联系)
平移 轴对称 旋转
相同点 都是全等变换,即变换前后的图形全等.
不同点
定义 把一个图形沿某一方向移动一定距离的图形变换 把一个图形沿着某一条直线折叠的图形变换 把一个图形绕着某一定点转动一个角度的图形变换
图形
要素 平移方向平移距离 对称轴 旋转中心、旋转方向、旋转角度
性质 连接各组对应点的线段平行(或共线)且相等. 任意一对对应点所连线段被对称轴垂直平分. 对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角.即对应点与旋转中心连线所成的角彼此相等.
旋转是九年级第三章所学内容,它是一种全等变形,其主要考点有中心对称图形,旋转作图等。判断中心对称图形是一个高频考点。在考试中可以把试卷倒过来看,如果正看与倒看图形是一模一样,就可以确定是中心对称图形。旋转需要掌握的第二个考点就是旋转的坐标变化,在解决相关问题时,一定要先弄清楚图形的性质,再弄清楚旋转中心、旋转方向和旋转角度。第三个考点为旋转性质与几何证明,旋转是全等变形,利用全等三角形的性质可以把具有数量关系,但是位置上比较零散的线段集中到一起,方便解决问题。
题型一(生活中的旋转现象)
1 下列运动属于旋转的是( )
A.足球在草地上滚动 B.火箭升空的运动
C.汽车在急刹车时向前滑行 D.钟表的钟摆动的过程
2 下列现象中属于旋转的有( )个
①地下水位逐年下降 ②传送带的移动 ③方向盘的转动
④水龙头开关的转动 ⑤钟摆的运动 ⑥荡秋千运动
A.5 B.4 C.3 D.2
题型二(利用旋转的性质求解)
1. 如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
A.90° B.75° C.60° D.45°
2. 如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°﹣α B.α C.180°﹣α D.2α
【解析】
由题意可得,∠CBD=α,∠ACB=∠EDB,
∵∠EDB+∠ADB=180°,
∴∠ADB+∠ACB=180°,
∵∠ADB+∠DBC+∠BCA+∠CAD=360°,∠CBD=α,
∴∠CAD=180° α,故选C.
题型二(利用旋转的性质求解)
题型三(理解中心对称)
1.下面说法正确的是( )
A.全等的两个图形成中心对称
B.能够完全重合的两个图形成中心对称
C.旋转后能重合的两个图形成中心对称
D.旋转180°后能重合的两个图形成中心对称
2.若两个图形成中心对称,则下列说法:①对应点的连线必经过对称中心;②这两个图形的形状和大小完全相同;③这两个图形的对应线段一定相等;④将一个图形绕对称中心旋转180°后必与另一个图形重合.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
题型四(利用中心对称的性质求解)
题型五(判断对称中心)
1 如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心.
题型五(判断对称中心)
轴对称图形 中心对称图形
图形 对称轴条数 图形 对称中心
线段 2条 中点
角 1条
等腰三角形 1条
等边三角形 3条
平行四边形 对角线交点
矩形 2条 对角线交点
菱形 2条 对角线交点
正方形 4条 对角线交点
圆 无数条 圆心
2.指出下面常见几何图形的对称轴条数和对称中心.
×
×
×
×
题型六(判断中心对称图形)
1 判断下列图形是否为中心对称图形.若是画√,不是画×
×
√
×
×
×
√
√
√
√
√
×
√
题型六(判定中心对称图形)
4.在 ①平行四边形、 ②正方形、 ③等边三角形、 ④等腰梯形、 ⑤菱形、 ⑥圆、⑦正八边形这些图形中,既是轴对称图形又是中心对称图形的是_____________(填序号)
5.下列四张扑克牌图案,属于中心对称图形的是( )
②⑤⑥⑦
B
题型七(关于原点对称的点的坐标的关系)
【详解】解:∵点A(a,2018)与点A′( 2019,b)是关于原点O的对称点,
∴a=2019,b= 2018,∴a+b=1,故选A.
题型七(关于原点对称的点的坐标的关系)
题型七(关于原点对称的点的坐标的关系)
【解答】根据题意,得(x2+2x)+(x+2)=0,y=-3.
∴x1=-1,x2=-2.
∵点P在第二象限,
∴x2+2x<0.∴x=-1.
∴x+2y=-7.
题型七(关于原点对称的点的坐标的关系)
7 直角坐标系中,点A(﹣3,4)与点B(3,﹣4)关于( )
A.x轴轴对称 B.y轴轴对称 C.原点中心对称 D.以上都不对
8 已知点P(2+m,n-3)与点Q(m,1+n)关于原点对称,则m-n的值是( )
A.1 B.-1 C.2 D.-2
题型八(图案设计)
题型八(图案设计)
3 如图,有一个4×4的正方形网格,网格中每个小正方形的边长为1.请你以左上角的三角形为基本图形,通过平移、轴对称或旋转,在网格中设计一个图案,使其既是轴对称图形,又是以点O为对称中心的中心对称图形.所作图案用阴影标识,且图案的面积为4(即阴影部分面积为4).
O
题型八(图案设计)
4 如图,下列4×4网格图是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(2)在下图中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
旋转是初中几何的一个重难点,而且旋转常作为中考命题者重点考虑的命题方向。由旋转产生的图形与关系非常多,且灵活多变,可以考查的知识点非常多,例如考查三角形全等与相似、四边形、圆,勾股定理等,更能考查学生综合能力,常以压轴题的形式出现。
2022年中考真题
1.(2022·上海·统考中考真题)有一个正n边形旋转90°后与自身重合,则n为( )
A.6 B.9 C.12 D.15
2022年中考真题
2023年中考真题
3.(2023·江西·统考中考真题)下列图形中,是中心对称图形的是( )
4.(2023·四川宜宾·统考中考真题)下列图案中,既是轴对称图形,又是中心对称图形的是( )
B
D
2022年中考真题
2022年中考真题
2023年中考真题
1
2022年中考真题
9.(2022益阳市中考)如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,以下结论:①BC=B′C′,②AC∥C′B′,③C′B′⊥BB′,④∠ABB′=∠ACC′,正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
【详解】解:①∵△ABC绕A点逆时针旋转50°得到△AB′C′,∴BC=B′C′.故①正确;
②∵△ABC绕A点逆时针旋转50°,∴∠BAB′=50°.
∵∠CAB=20°,∴∠B′AC=∠BAB′﹣∠CAB=30°.
∵∠AB′C′=∠ABC=30°,∴∠AB′C′=∠B′AC.∴AC∥C′B′.故②正确;
③在△BAB′中,AB=AB′,∠BAB′=50°,∴∠AB′B=∠ABB′=(180°﹣50°)/2=65°.∴∠BB′C′=∠AB′B+∠AB′C′=65°+30°=95°.∴CB′与BB′不垂直.故③不正确;
④在△ACC′中,AC=AC′,∠CAC′=50°,∴∠ACC′=(180°﹣50°)/2=65°.
∴∠ABB′=∠ACC′.故④正确.∴①②④这三个结论正确.故选:B.
2022年中考真题
2023年中考真题
学习目标
1 了解图形的旋转的有关概念并理解它的基本性质;
2 了解中心对称和中心对称图形的概念并理解它的基本性质;
3 掌握关于原点对称的两点的关系并应用。
本章重点内容:
1 理解并掌握图形旋转和中心对称基本性质。
2 两个点关于原点对称时,它们坐标之间的关系。
本章难点内容:
1 图形旋转的基本性质的归纳与运用。
2 中心对称的基本性质的归纳与运用。
让学生经历观察、操作等过程,了解图形旋转的概念,探索图形旋转基本性质,进一步发展空间观察,培养运动几何的观点,增强审美意识。让学生通过独立思考,自主探究和合作交流进一步体会旋转的数学内涵,享受学习乐趣,学生运用所学知识进行图案设计活动,激发学习热情。
基础巩固(旋转)
在平面内,将一个平面图形绕着平面内一个定点沿某一方向转动一个角度,就叫做图形的旋转.这个定点叫做旋转中心.转动的角叫做旋转角.
O
[提问]如果图形上的点P经过旋转变为点P′,那么点P和P′叫做这个旋转的________.
旋转中心是_________,旋转角度是_________.
旋转方向__________.
点O
120°
P′
对应点
120°
P
顺时针
基础巩固(旋转的性质)
1.对应点到旋转中心的距离相等.
2.对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等.
基础巩固(旋转作图的一般步骤)
1)找出图形的关键点;
2)确定旋转中心,旋转方向和旋转角;
3)将关键点与旋转中心连接起来,然后按旋转方向分别将它们旋转一个角,得到关键点的对应点;
4)按照原图形的顺序连接这些对应点,所得到的图形就是旋转后的图形.
基础巩固(中心对称)
把一个图形绕某一个点旋转180 ,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称.
1)这个点叫做对称中心.
2)这两个图形中的对应点叫做关于中心的对称点.
A
B
O
C
D
[提问]
1)你能指出图中的对称点吗?
2)点C、点A、点O的位置关系怎样
3)线段AO、OC的大小关系呢
点A与点C、点B与点D
在一条直线上
相等
基础巩固(中心对称的性质)
1)中心对称的两个图形,对称点所连线段经过对称中心,而且被对称中心所平分.
2)中心对称的两个图形是全等形.
基础巩固(旋转与中心对称)
旋转 中心对称
图形
性质
1 对应点与旋转中心所连线段的夹角等于旋转角 对称点所连线段都经过对称中心
2 对应点到旋转中心的距离相等 对称点所连线段被对称中心所平分
3 旋转前、后的图形全等 关于中心对称的两个图形是全等图形
基础巩固(中心对称图形)
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
平行四边形
O
A
B
C
D
[提问]
1)你能指出图中的中心对称图形吗?
2)你能指出图中的对称点吗?
3)你能指出图中的对称中心吗?
ABCD
点O
点A与点C、点B与点D
基础巩固(中心对称与中心对称图形的区别与联系)
名称 中心对称 中心对称图形
定义 把一个图形绕着某一个点旋转180 ,如果他能够与另一个图形重合,那么就说这两个图形关于这点对称或中心对称 如果一个图形绕着一个点旋转180 后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形
性质 ①两个图形可完全重合;
②对应点连线都经过对称中心,并且被对称中心平分 ①是一个特殊的图形
②对应点连线都经过对称中心,并且被对称中心平分
区别 ①两个图形的关系
②对称点在两个图形上 ①具有某种性质的一个图形
②对称点在一个图形上
联系 若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,
若把中心对称的两个图形看作一个整体,则成为中心对称图形。
基础巩固(关于原点对称的点的坐标的关系)
两个点关于原点对称时,它们的坐标符号相反,
P(x,y)
P′ (–x,–y)
关于原点O的对称点
P(x,y)
P′ (x,–y)
关于x轴的对称点
P(x,y)
P′ (–x,y)
关于y轴的对称点
横、纵坐标都互为相反数
纵坐标相同,横坐标互为相反数
横坐标相同,纵坐标互为相反数
基础巩固(平移、轴对称、旋转的区别与联系)
平移 轴对称 旋转
相同点 都是全等变换,即变换前后的图形全等.
不同点
定义 把一个图形沿某一方向移动一定距离的图形变换 把一个图形沿着某一条直线折叠的图形变换 把一个图形绕着某一定点转动一个角度的图形变换
图形
要素 平移方向平移距离 对称轴 旋转中心、旋转方向、旋转角度
性质 连接各组对应点的线段平行(或共线)且相等. 任意一对对应点所连线段被对称轴垂直平分. 对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角.即对应点与旋转中心连线所成的角彼此相等.
旋转是九年级第三章所学内容,它是一种全等变形,其主要考点有中心对称图形,旋转作图等。判断中心对称图形是一个高频考点。在考试中可以把试卷倒过来看,如果正看与倒看图形是一模一样,就可以确定是中心对称图形。旋转需要掌握的第二个考点就是旋转的坐标变化,在解决相关问题时,一定要先弄清楚图形的性质,再弄清楚旋转中心、旋转方向和旋转角度。第三个考点为旋转性质与几何证明,旋转是全等变形,利用全等三角形的性质可以把具有数量关系,但是位置上比较零散的线段集中到一起,方便解决问题。
题型一(生活中的旋转现象)
1 下列运动属于旋转的是( )
A.足球在草地上滚动 B.火箭升空的运动
C.汽车在急刹车时向前滑行 D.钟表的钟摆动的过程
2 下列现象中属于旋转的有( )个
①地下水位逐年下降 ②传送带的移动 ③方向盘的转动
④水龙头开关的转动 ⑤钟摆的运动 ⑥荡秋千运动
A.5 B.4 C.3 D.2
题型二(利用旋转的性质求解)
1. 如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
A.90° B.75° C.60° D.45°
2. 如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°﹣α B.α C.180°﹣α D.2α
【解析】
由题意可得,∠CBD=α,∠ACB=∠EDB,
∵∠EDB+∠ADB=180°,
∴∠ADB+∠ACB=180°,
∵∠ADB+∠DBC+∠BCA+∠CAD=360°,∠CBD=α,
∴∠CAD=180° α,故选C.
题型二(利用旋转的性质求解)
题型三(理解中心对称)
1.下面说法正确的是( )
A.全等的两个图形成中心对称
B.能够完全重合的两个图形成中心对称
C.旋转后能重合的两个图形成中心对称
D.旋转180°后能重合的两个图形成中心对称
2.若两个图形成中心对称,则下列说法:①对应点的连线必经过对称中心;②这两个图形的形状和大小完全相同;③这两个图形的对应线段一定相等;④将一个图形绕对称中心旋转180°后必与另一个图形重合.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
题型四(利用中心对称的性质求解)
题型五(判断对称中心)
1 如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心.
题型五(判断对称中心)
轴对称图形 中心对称图形
图形 对称轴条数 图形 对称中心
线段 2条 中点
角 1条
等腰三角形 1条
等边三角形 3条
平行四边形 对角线交点
矩形 2条 对角线交点
菱形 2条 对角线交点
正方形 4条 对角线交点
圆 无数条 圆心
2.指出下面常见几何图形的对称轴条数和对称中心.
×
×
×
×
题型六(判断中心对称图形)
1 判断下列图形是否为中心对称图形.若是画√,不是画×
×
√
×
×
×
√
√
√
√
√
×
√
题型六(判定中心对称图形)
4.在 ①平行四边形、 ②正方形、 ③等边三角形、 ④等腰梯形、 ⑤菱形、 ⑥圆、⑦正八边形这些图形中,既是轴对称图形又是中心对称图形的是_____________(填序号)
5.下列四张扑克牌图案,属于中心对称图形的是( )
②⑤⑥⑦
B
题型七(关于原点对称的点的坐标的关系)
【详解】解:∵点A(a,2018)与点A′( 2019,b)是关于原点O的对称点,
∴a=2019,b= 2018,∴a+b=1,故选A.
题型七(关于原点对称的点的坐标的关系)
题型七(关于原点对称的点的坐标的关系)
【解答】根据题意,得(x2+2x)+(x+2)=0,y=-3.
∴x1=-1,x2=-2.
∵点P在第二象限,
∴x2+2x<0.∴x=-1.
∴x+2y=-7.
题型七(关于原点对称的点的坐标的关系)
7 直角坐标系中,点A(﹣3,4)与点B(3,﹣4)关于( )
A.x轴轴对称 B.y轴轴对称 C.原点中心对称 D.以上都不对
8 已知点P(2+m,n-3)与点Q(m,1+n)关于原点对称,则m-n的值是( )
A.1 B.-1 C.2 D.-2
题型八(图案设计)
题型八(图案设计)
3 如图,有一个4×4的正方形网格,网格中每个小正方形的边长为1.请你以左上角的三角形为基本图形,通过平移、轴对称或旋转,在网格中设计一个图案,使其既是轴对称图形,又是以点O为对称中心的中心对称图形.所作图案用阴影标识,且图案的面积为4(即阴影部分面积为4).
O
题型八(图案设计)
4 如图,下列4×4网格图是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(2)在下图中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
旋转是初中几何的一个重难点,而且旋转常作为中考命题者重点考虑的命题方向。由旋转产生的图形与关系非常多,且灵活多变,可以考查的知识点非常多,例如考查三角形全等与相似、四边形、圆,勾股定理等,更能考查学生综合能力,常以压轴题的形式出现。
2022年中考真题
1.(2022·上海·统考中考真题)有一个正n边形旋转90°后与自身重合,则n为( )
A.6 B.9 C.12 D.15
2022年中考真题
2023年中考真题
3.(2023·江西·统考中考真题)下列图形中,是中心对称图形的是( )
4.(2023·四川宜宾·统考中考真题)下列图案中,既是轴对称图形,又是中心对称图形的是( )
B
D
2022年中考真题
2022年中考真题
2023年中考真题
1
2022年中考真题
9.(2022益阳市中考)如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,以下结论:①BC=B′C′,②AC∥C′B′,③C′B′⊥BB′,④∠ABB′=∠ACC′,正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
【详解】解:①∵△ABC绕A点逆时针旋转50°得到△AB′C′,∴BC=B′C′.故①正确;
②∵△ABC绕A点逆时针旋转50°,∴∠BAB′=50°.
∵∠CAB=20°,∴∠B′AC=∠BAB′﹣∠CAB=30°.
∵∠AB′C′=∠ABC=30°,∴∠AB′C′=∠B′AC.∴AC∥C′B′.故②正确;
③在△BAB′中,AB=AB′,∠BAB′=50°,∴∠AB′B=∠ABB′=(180°﹣50°)/2=65°.∴∠BB′C′=∠AB′B+∠AB′C′=65°+30°=95°.∴CB′与BB′不垂直.故③不正确;
④在△ACC′中,AC=AC′,∠CAC′=50°,∴∠ACC′=(180°﹣50°)/2=65°.
∴∠ABB′=∠ACC′.故④正确.∴①②④这三个结论正确.故选:B.
2022年中考真题
2023年中考真题
同课章节目录
