第1章反比例函数 同步练习题 湘教版九年级数学上册(含解析)
文档属性
| 名称 | 第1章反比例函数 同步练习题 湘教版九年级数学上册(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 211.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-19 14:15:35 | ||
图片预览

文档简介
2023-2024学年湘教版九年级数学上册《第1章反比例函数》同步练习题(附答案)
一.选择题
1.正比例函数y=2x和反比例函数的一个交点为(1,2),则另一个交点为( )
A.(﹣1,﹣2) B.(﹣2,﹣1) C.(1,2) D.(2,1)
2.如图,直线y=mx与双曲线y=交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=2,则k的值是( )
A.2 B.m﹣2 C.m D.4
3.函数y=xk﹣1是反比例函数,则k=( )
A.0 B.1 C.2 D.3
4.反比例函数y=﹣与一次函数y=x﹣2在同一坐标系中的大致图象可能是( )
A. B.
C. D.
5.已知反比例函数图象如图所示,下列说法正确的是( )
A.k>0 B.y随x的增大而减小
C.若矩形OABC面积为2,则k=2
D.若图象上两个点的坐标分别是M(﹣2,y1),N(﹣1,y2),则y1<y2
6.若点(x1,y1),(x2,y2),(x3,y3)都在反比例函数y=的图象上,且x1<x2<0<x3,则( )
A.y1>y2>y3 B.y2>y1>y3 C.y3>y1>y2 D.y1>y3>y2
7.如图,函数y1=x+1与函数y2=的图象交于M(1,m)和N(﹣2,n)两点,若y1<y2,则x的取值范围是( )
A.x<﹣2或0<x<1 B.x<﹣2或x>1
C.﹣2<x<0或0<x<1 D.﹣2<x<0或x>1
8.如图,点A、B在反比函数y=的图象上,A、B的纵坐标分别是3和6,连接OA、OB,则△OAB的面积是( )
A.9 B.8 C.7 D.6
9.如图,在平面直角坐标系中,点A在函数y=﹣的图象上,点B在函数y=的图象上,若AO=2BO,∠AOB=90°,则k的值为( )
A.0.5 B.1 C.1.5 D.2
10.如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,对角线OB、AC交于点D,点A(6,0),∠AOC=60°,反比例函数的图象经过点D,则k的值为( )
A. B. C. D.
二.填空题
11.如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .
12.如图,点A是反比例函数y=的图象上一点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=的图象于点C,则△OAC的面积为 .
13.如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为3,则这个反比例函数的解析式为 .
14.已知函数y=﹣,当自变量的取值为﹣1<x<0或x≥2,函数值y的取值 .
15.近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知250度近视眼镜镜片的焦距为0.4米,则眼镜度数y与镜片焦距x之间的函数关系式为 .
16.在“2011年北京郁金香文化节”中,北京国际鲜花港的3×106株郁金香为京城增添了亮丽的色彩.若这些郁金香平均每平方米种植的数量为n(单位:株/平方米),总种植面积为S(单位:平方米),则n与S的函数关系式为 .(不要求写出自变量S的取值范围)
三.解答题
17.如图,已知反比例函数y=的图象与一次函数y=ax+b的图象交于M(2,m)和N(﹣1,﹣4)两点.
(1)求这两个函数的解析式;
(2)求△MON的面积;
(3)请判断点P(4,1)是否在这个反比例函数的图象上,并说明理由;
(4)根据图象,若ax+b<时,直接写出x取值范围.
18.为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
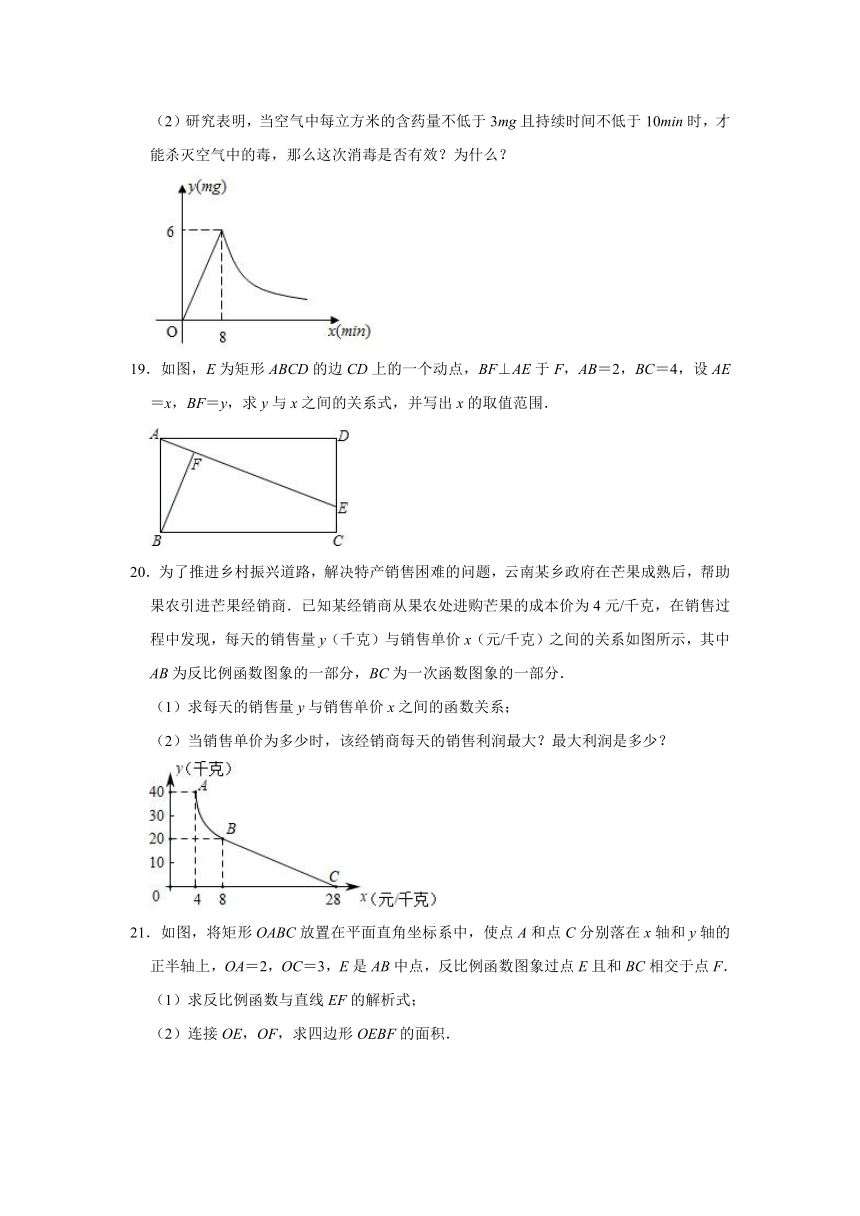
(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
19.如图,E为矩形ABCD的边CD上的一个动点,BF⊥AE于F,AB=2,BC=4,设AE=x,BF=y,求y与x之间的关系式,并写出x的取值范围.
20.为了推进乡村振兴道路,解决特产销售困难的问题,云南某乡政府在芒果成熟后,帮助果农引进芒果经销商.已知某经销商从果农处进购芒果的成本价为4元/千克,在销售过程中发现,每天的销售量y(千克)与销售单价x(元/千克)之间的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.
(1)求每天的销售量y与销售单价x之间的函数关系;
(2)当销售单价为多少时,该经销商每天的销售利润最大?最大利润是多少?
21.如图,将矩形OABC放置在平面直角坐标系中,使点A和点C分别落在x轴和y轴的正半轴上,OA=2,OC=3,E是AB中点,反比例函数图象过点E且和BC相交于点F.
(1)求反比例函数与直线EF的解析式;
(2)连接OE,OF,求四边形OEBF的面积.
22.如图,已知反比例函数y1=与一次函数y2=k2x+b的图象交于点A(1,8)、B(﹣4,m).
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)若y1<y2,求x的取值范围.
参考答案
一.选择题
1.解:∵正比例函数y=2x和反比例函数的一个交点为(1,2),
∴另一个交点与点(1,2)关于原点对称,
∴另一个交点是(﹣1,﹣2).
故选:A.
2.解:设A(x,y),
∵直线y=mx与双曲线y=交于A、B两点,
∴B(﹣x,﹣y),
∴S△BOM=|xy|,S△AOM=|xy|,
∴S△BOM=S△AOM,
∴S△ABM=S△AOM+S△BOM=2S△AOM=2,S△AOM=|k|=1,则k=±2.
又由于反比例函数位于一三象限,k>0,故k=2.
故选:A.
3.解:由题意得:k﹣1=﹣1,
解得:k=0,
故选:A.
4.解:由反比例函数y=﹣与一次函数y=x﹣2可知,反比例函数的图象在二、四象限,一次函数的图象通过一、三、四象限,
故选:C.
5.解:如图,k<0,y随x的增大而增大;
∵矩形OABC面积为2,k=﹣2,
故选:D.
6.解:∵反比例函数y=中k=5>0,
∴函数图象的两个分支分别位于一、三象限,且在每一象限内,y随x的增大而减小.
∵x1<x2<0,
∴A、B两点在第三象限,C点在第一象限,
∴y3>y1>y2.
故选:C.
7.解:由图象可知,y1<y2时的x的取值范围为x<﹣2或0<x<1,
故选:A.
8.解:∵点A、B在反比例函数y=的图象上,A、B的纵坐标分别是3和6,
∴A(4,3),B(2,6),
作AD⊥y轴于D,BE⊥y轴于E,
∴S△AOD=S△BOE=×12=6,
∵S△OAB=S△AOD+S梯形ABED﹣S△BOE=S梯形ABED,
∴S△AOB=(4+2)×(6﹣3)=9,
故选:A.
9.解:如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
∴∠ACO=∠BDO=90°,
∴∠AOC+∠OAC=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠BOD=∠OAC,
∵AO=2BO,
∴S△AOC:S△BOD=4,
∵点A在函数y=﹣的图象上,点B在函数y=的图象上,
∴S△AOC=×|﹣8|=4,S△BOD=k,
∴4=4×(k),解得k=2,
故选:D.
10.解:过C作CM⊥x轴于M,
∵点A(6,0),
∴OA=6,
∵四边形ABCO是菱形,
∴OC=OA=6,D是AC的中点,
∵∠AOC=60°,
∴OM=OC=3,CM=OC=3,
∴C(3,3),
∴D点的坐标是(,),
∵反比例函数的图像经过点D,
∴k=×=,
故选:A.
二.填空题
11.解:延长BA交y轴于E,
∵AB∥x轴,
∴AE垂直于y轴,
∵点A在双曲线上,
∴四边形AEOD的面积为1,
∵点B在双曲线y=上,且AB∥x轴,
∴四边形BEOC的面积为3,
∴矩形ABCD的面积为3﹣1=2.
故答案为:2.
12.解:∵AB⊥x轴,
∴S△AOB=×|6|=3,S△COB=×|2|=1,
∴S△AOC=S△AOB﹣S△COB=2.
故答案为:2.
13.解:过A点向x轴作垂线,如图:
根据反比例函数的几何意义可得:四边形ABCD的面积为3,即|k|=3,
又∵函数图象在二、四象限,
∴k=﹣3,即函数解析式为:y=﹣.
故答案为:y=﹣.
14.解:当x=﹣1时,y=﹣=1,
当x=2时,y=﹣,
由图象得:当﹣1<x<0时,y>1,
当x≥2时,﹣≤y<0,
故答案为:y>1或﹣≤y<0.
15.解:根据题意近视眼镜的度数y(度)与镜片焦距x(米)成反比例,设y=,
由于点(0.4,250)在此函数解析式上,
∴k=0.4×250=100,
∴y=
故答案为y=.
16.解:由题意得:郁金香的总数量为3×106株,平均每平方米种植的数量为n,总种植面积为S,
∴可得:n=.
故答案为:n=.
三.解答题
17.解:(1)∵把N(﹣1,﹣4)代入y=得:k=4,
∴反比例函数的解析式是y=,
∵M(2,m)代入反比例函数y=得:m=2,
∴N的坐标是(2,2),
把M、N的坐标代入一次函数y=ax+b得:,
解得:,
∴一次函数的解析式是y=2x﹣2;
(2)∵把y=0代入一次函数的解析式是y=2x﹣2得:0=2x﹣2,
解得x=1,
∴A(1,0),
∴△MON的面积S=SAOM+S△AON=×1×2+×1×4=3;
(3)把x=4代入y=得,y=1,
∴点P(4,1)在这个反比例函数的图象上;
(4)从图象可知:ax+b<时x的取值范围x<﹣1或0<x<2.
18.解:(1)设药物燃烧时y关于x的函数关系式为y=k1x(k1>0),
代入(8,6)得6=8k1,
∴k1=,
设药物燃烧后y关于x的函数关系式为y=(k2>0),
代入(8,6)得6=,
∴k2=48,
∴药物燃烧时y关于x的函数关系式为(0≤x≤8)药物燃烧后y关于x的函数关系式为:(x>8),
∴;
(2)有效,理由如下:
把y=3代入,得:x=4,
把y=3代入,得:x=16,
∵16﹣4=12,
∴这次消毒是有效的.
19.解:如图,连接AC.
∵BF⊥AE于F,四边形ABCD是矩形,
∴∠D=∠AFB=∠BAD=90°,AD=BC=4,
∴∠ABF+∠BAF=90°,∠BAF+∠DAE=90°,AC==2,
∴∠ABF=∠DAE,
∴cos∠ABF=,cos∠DAE=,
∴=,
y=(4≤x≤2).
20.解:(1)当4≤x≤8时,设y与x的函数关系式为y=,
∵点(4,40)在该函数图象上,
∴40=,得k=160,
∴当4≤x≤8时,y与x的函数关系式为y=,
当8<x≤28时,设y与x的函数关系式为y=ax+b,
,
解得,
即当8<x≤28时,y与x的函数关系式为y=﹣x+28,
由上可得y=;
(2)设利润为w元,
当4≤x≤8时,w=(x﹣4)y=(x﹣4) =160﹣,
∵k=﹣640,
∴y随x的增大而增大,
∴当x=8时,w取得最大值,此时w=160﹣=80,
当8<x≤28时,w=(x﹣4)y=(x﹣4)(﹣x+28)=﹣(x﹣16)2+144,
∴当x=16时,w取得最大值,此时w=144,
∵144>80,
∴当销售单价为16时,该经销商每天的销售利润最大,最大利润是144元,
答:当销售单价为16时,该经销商每天的销售利润最大,最大利润是144元.
21.解:(1)∵OA=2,OC=3,E是AB中点,
∴B(2,3),E(2,),
设反比例函数的解析式为y=,
把E(2,)代入得,
解得:k1=3,
∴反比例函数的解析式为y=,
∴点F在BC上,
∴yF=3,
把yF=3代入y=得,xF=1,
∴F(1,3),
设直线EF的解析式为y=k2x+b,
把E(2,),F(1,3)代入得,,
解得:,
∴直线EF的解析式为y=﹣x+;
(2)S四边形OEBF=S矩形OABC﹣S△OCF﹣S△OAE=2×3﹣×1×3﹣×2×=3.
22.解:(1)点A(1,8)在反比例函数y1=上,
∴k1=1×8=8.
∴.
∵点B(﹣4,m)在反比例函数y1=上,
∴﹣4m=8.
∴m=﹣2.
∴B(﹣4,﹣2).
∵点A(1,8)、B(﹣4,﹣2)在一次函数y2=k2x+b的图象上,
∴,
解得:.
∴y2=2x+6.
∴k1=8,k2=2,b=6.
(2)设直线AB与x轴交于点D,与y轴交于点C,如图,
令x=0,则y=6,
∴C(0,6).
∴OC=6.
令y=0,则2x+6=0,
解得:x=﹣3.
∴D(﹣3,0).
∴OD=3.
过点A作AE⊥y轴于点E过点B作BF⊥x轴于点F,
∵A(1,8),B(﹣4,﹣2),
∴AE=1,BF=2.
∴S△AOB=S△AOC+S△OCD+S△ODB
=×OC AE+OD OC+OD BF
=++
=3+9+3
=15;
(3)由图象可知,点A右侧的部分和点B与点C之间的部分y1<y2,
∴若y1<y2,x的取值范围为:﹣4<x<0或x>1.
一.选择题
1.正比例函数y=2x和反比例函数的一个交点为(1,2),则另一个交点为( )
A.(﹣1,﹣2) B.(﹣2,﹣1) C.(1,2) D.(2,1)
2.如图,直线y=mx与双曲线y=交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=2,则k的值是( )
A.2 B.m﹣2 C.m D.4
3.函数y=xk﹣1是反比例函数,则k=( )
A.0 B.1 C.2 D.3
4.反比例函数y=﹣与一次函数y=x﹣2在同一坐标系中的大致图象可能是( )
A. B.
C. D.
5.已知反比例函数图象如图所示,下列说法正确的是( )
A.k>0 B.y随x的增大而减小
C.若矩形OABC面积为2,则k=2
D.若图象上两个点的坐标分别是M(﹣2,y1),N(﹣1,y2),则y1<y2
6.若点(x1,y1),(x2,y2),(x3,y3)都在反比例函数y=的图象上,且x1<x2<0<x3,则( )
A.y1>y2>y3 B.y2>y1>y3 C.y3>y1>y2 D.y1>y3>y2
7.如图,函数y1=x+1与函数y2=的图象交于M(1,m)和N(﹣2,n)两点,若y1<y2,则x的取值范围是( )
A.x<﹣2或0<x<1 B.x<﹣2或x>1
C.﹣2<x<0或0<x<1 D.﹣2<x<0或x>1
8.如图,点A、B在反比函数y=的图象上,A、B的纵坐标分别是3和6,连接OA、OB,则△OAB的面积是( )
A.9 B.8 C.7 D.6
9.如图,在平面直角坐标系中,点A在函数y=﹣的图象上,点B在函数y=的图象上,若AO=2BO,∠AOB=90°,则k的值为( )
A.0.5 B.1 C.1.5 D.2
10.如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,对角线OB、AC交于点D,点A(6,0),∠AOC=60°,反比例函数的图象经过点D,则k的值为( )
A. B. C. D.
二.填空题
11.如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .
12.如图,点A是反比例函数y=的图象上一点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=的图象于点C,则△OAC的面积为 .
13.如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为3,则这个反比例函数的解析式为 .
14.已知函数y=﹣,当自变量的取值为﹣1<x<0或x≥2,函数值y的取值 .
15.近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知250度近视眼镜镜片的焦距为0.4米,则眼镜度数y与镜片焦距x之间的函数关系式为 .
16.在“2011年北京郁金香文化节”中,北京国际鲜花港的3×106株郁金香为京城增添了亮丽的色彩.若这些郁金香平均每平方米种植的数量为n(单位:株/平方米),总种植面积为S(单位:平方米),则n与S的函数关系式为 .(不要求写出自变量S的取值范围)
三.解答题
17.如图,已知反比例函数y=的图象与一次函数y=ax+b的图象交于M(2,m)和N(﹣1,﹣4)两点.
(1)求这两个函数的解析式;
(2)求△MON的面积;
(3)请判断点P(4,1)是否在这个反比例函数的图象上,并说明理由;
(4)根据图象,若ax+b<时,直接写出x取值范围.
18.为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
19.如图,E为矩形ABCD的边CD上的一个动点,BF⊥AE于F,AB=2,BC=4,设AE=x,BF=y,求y与x之间的关系式,并写出x的取值范围.
20.为了推进乡村振兴道路,解决特产销售困难的问题,云南某乡政府在芒果成熟后,帮助果农引进芒果经销商.已知某经销商从果农处进购芒果的成本价为4元/千克,在销售过程中发现,每天的销售量y(千克)与销售单价x(元/千克)之间的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.
(1)求每天的销售量y与销售单价x之间的函数关系;
(2)当销售单价为多少时,该经销商每天的销售利润最大?最大利润是多少?
21.如图,将矩形OABC放置在平面直角坐标系中,使点A和点C分别落在x轴和y轴的正半轴上,OA=2,OC=3,E是AB中点,反比例函数图象过点E且和BC相交于点F.
(1)求反比例函数与直线EF的解析式;
(2)连接OE,OF,求四边形OEBF的面积.
22.如图,已知反比例函数y1=与一次函数y2=k2x+b的图象交于点A(1,8)、B(﹣4,m).
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)若y1<y2,求x的取值范围.
参考答案
一.选择题
1.解:∵正比例函数y=2x和反比例函数的一个交点为(1,2),
∴另一个交点与点(1,2)关于原点对称,
∴另一个交点是(﹣1,﹣2).
故选:A.
2.解:设A(x,y),
∵直线y=mx与双曲线y=交于A、B两点,
∴B(﹣x,﹣y),
∴S△BOM=|xy|,S△AOM=|xy|,
∴S△BOM=S△AOM,
∴S△ABM=S△AOM+S△BOM=2S△AOM=2,S△AOM=|k|=1,则k=±2.
又由于反比例函数位于一三象限,k>0,故k=2.
故选:A.
3.解:由题意得:k﹣1=﹣1,
解得:k=0,
故选:A.
4.解:由反比例函数y=﹣与一次函数y=x﹣2可知,反比例函数的图象在二、四象限,一次函数的图象通过一、三、四象限,
故选:C.
5.解:如图,k<0,y随x的增大而增大;
∵矩形OABC面积为2,k=﹣2,
故选:D.
6.解:∵反比例函数y=中k=5>0,
∴函数图象的两个分支分别位于一、三象限,且在每一象限内,y随x的增大而减小.
∵x1<x2<0,
∴A、B两点在第三象限,C点在第一象限,
∴y3>y1>y2.
故选:C.
7.解:由图象可知,y1<y2时的x的取值范围为x<﹣2或0<x<1,
故选:A.
8.解:∵点A、B在反比例函数y=的图象上,A、B的纵坐标分别是3和6,
∴A(4,3),B(2,6),
作AD⊥y轴于D,BE⊥y轴于E,
∴S△AOD=S△BOE=×12=6,
∵S△OAB=S△AOD+S梯形ABED﹣S△BOE=S梯形ABED,
∴S△AOB=(4+2)×(6﹣3)=9,
故选:A.
9.解:如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
∴∠ACO=∠BDO=90°,
∴∠AOC+∠OAC=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠BOD=∠OAC,
∵AO=2BO,
∴S△AOC:S△BOD=4,
∵点A在函数y=﹣的图象上,点B在函数y=的图象上,
∴S△AOC=×|﹣8|=4,S△BOD=k,
∴4=4×(k),解得k=2,
故选:D.
10.解:过C作CM⊥x轴于M,
∵点A(6,0),
∴OA=6,
∵四边形ABCO是菱形,
∴OC=OA=6,D是AC的中点,
∵∠AOC=60°,
∴OM=OC=3,CM=OC=3,
∴C(3,3),
∴D点的坐标是(,),
∵反比例函数的图像经过点D,
∴k=×=,
故选:A.
二.填空题
11.解:延长BA交y轴于E,
∵AB∥x轴,
∴AE垂直于y轴,
∵点A在双曲线上,
∴四边形AEOD的面积为1,
∵点B在双曲线y=上,且AB∥x轴,
∴四边形BEOC的面积为3,
∴矩形ABCD的面积为3﹣1=2.
故答案为:2.
12.解:∵AB⊥x轴,
∴S△AOB=×|6|=3,S△COB=×|2|=1,
∴S△AOC=S△AOB﹣S△COB=2.
故答案为:2.
13.解:过A点向x轴作垂线,如图:
根据反比例函数的几何意义可得:四边形ABCD的面积为3,即|k|=3,
又∵函数图象在二、四象限,
∴k=﹣3,即函数解析式为:y=﹣.
故答案为:y=﹣.
14.解:当x=﹣1时,y=﹣=1,
当x=2时,y=﹣,
由图象得:当﹣1<x<0时,y>1,
当x≥2时,﹣≤y<0,
故答案为:y>1或﹣≤y<0.
15.解:根据题意近视眼镜的度数y(度)与镜片焦距x(米)成反比例,设y=,
由于点(0.4,250)在此函数解析式上,
∴k=0.4×250=100,
∴y=
故答案为y=.
16.解:由题意得:郁金香的总数量为3×106株,平均每平方米种植的数量为n,总种植面积为S,
∴可得:n=.
故答案为:n=.
三.解答题
17.解:(1)∵把N(﹣1,﹣4)代入y=得:k=4,
∴反比例函数的解析式是y=,
∵M(2,m)代入反比例函数y=得:m=2,
∴N的坐标是(2,2),
把M、N的坐标代入一次函数y=ax+b得:,
解得:,
∴一次函数的解析式是y=2x﹣2;
(2)∵把y=0代入一次函数的解析式是y=2x﹣2得:0=2x﹣2,
解得x=1,
∴A(1,0),
∴△MON的面积S=SAOM+S△AON=×1×2+×1×4=3;
(3)把x=4代入y=得,y=1,
∴点P(4,1)在这个反比例函数的图象上;
(4)从图象可知:ax+b<时x的取值范围x<﹣1或0<x<2.
18.解:(1)设药物燃烧时y关于x的函数关系式为y=k1x(k1>0),
代入(8,6)得6=8k1,
∴k1=,
设药物燃烧后y关于x的函数关系式为y=(k2>0),
代入(8,6)得6=,
∴k2=48,
∴药物燃烧时y关于x的函数关系式为(0≤x≤8)药物燃烧后y关于x的函数关系式为:(x>8),
∴;
(2)有效,理由如下:
把y=3代入,得:x=4,
把y=3代入,得:x=16,
∵16﹣4=12,
∴这次消毒是有效的.
19.解:如图,连接AC.
∵BF⊥AE于F,四边形ABCD是矩形,
∴∠D=∠AFB=∠BAD=90°,AD=BC=4,
∴∠ABF+∠BAF=90°,∠BAF+∠DAE=90°,AC==2,
∴∠ABF=∠DAE,
∴cos∠ABF=,cos∠DAE=,
∴=,
y=(4≤x≤2).
20.解:(1)当4≤x≤8时,设y与x的函数关系式为y=,
∵点(4,40)在该函数图象上,
∴40=,得k=160,
∴当4≤x≤8时,y与x的函数关系式为y=,
当8<x≤28时,设y与x的函数关系式为y=ax+b,
,
解得,
即当8<x≤28时,y与x的函数关系式为y=﹣x+28,
由上可得y=;
(2)设利润为w元,
当4≤x≤8时,w=(x﹣4)y=(x﹣4) =160﹣,
∵k=﹣640,
∴y随x的增大而增大,
∴当x=8时,w取得最大值,此时w=160﹣=80,
当8<x≤28时,w=(x﹣4)y=(x﹣4)(﹣x+28)=﹣(x﹣16)2+144,
∴当x=16时,w取得最大值,此时w=144,
∵144>80,
∴当销售单价为16时,该经销商每天的销售利润最大,最大利润是144元,
答:当销售单价为16时,该经销商每天的销售利润最大,最大利润是144元.
21.解:(1)∵OA=2,OC=3,E是AB中点,
∴B(2,3),E(2,),
设反比例函数的解析式为y=,
把E(2,)代入得,
解得:k1=3,
∴反比例函数的解析式为y=,
∴点F在BC上,
∴yF=3,
把yF=3代入y=得,xF=1,
∴F(1,3),
设直线EF的解析式为y=k2x+b,
把E(2,),F(1,3)代入得,,
解得:,
∴直线EF的解析式为y=﹣x+;
(2)S四边形OEBF=S矩形OABC﹣S△OCF﹣S△OAE=2×3﹣×1×3﹣×2×=3.
22.解:(1)点A(1,8)在反比例函数y1=上,
∴k1=1×8=8.
∴.
∵点B(﹣4,m)在反比例函数y1=上,
∴﹣4m=8.
∴m=﹣2.
∴B(﹣4,﹣2).
∵点A(1,8)、B(﹣4,﹣2)在一次函数y2=k2x+b的图象上,
∴,
解得:.
∴y2=2x+6.
∴k1=8,k2=2,b=6.
(2)设直线AB与x轴交于点D,与y轴交于点C,如图,
令x=0,则y=6,
∴C(0,6).
∴OC=6.
令y=0,则2x+6=0,
解得:x=﹣3.
∴D(﹣3,0).
∴OD=3.
过点A作AE⊥y轴于点E过点B作BF⊥x轴于点F,
∵A(1,8),B(﹣4,﹣2),
∴AE=1,BF=2.
∴S△AOB=S△AOC+S△OCD+S△ODB
=×OC AE+OD OC+OD BF
=++
=3+9+3
=15;
(3)由图象可知,点A右侧的部分和点B与点C之间的部分y1<y2,
∴若y1<y2,x的取值范围为:﹣4<x<0或x>1.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
