数学人教A版(2019)选择性必修第一册1.2空间向量基本定理 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.2空间向量基本定理 课件(共15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 485.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 11:43:19 | ||
图片预览






文档简介
(共15张PPT)
第一章 统计案例
1.2
空间向量的基本定理
学习目标
1.理解空间向量基本定理;
2.理解基底、基向量及向量的坐标表示、正交分解的概念;
3.会用空间向量基本定理解决立体几何的简单问题.
4.核心素养:数学建模、数学运算。
1.平面向量基本定理:
2.平面向量的正交分解及坐标表示
x
y
o
一、回顾旧知
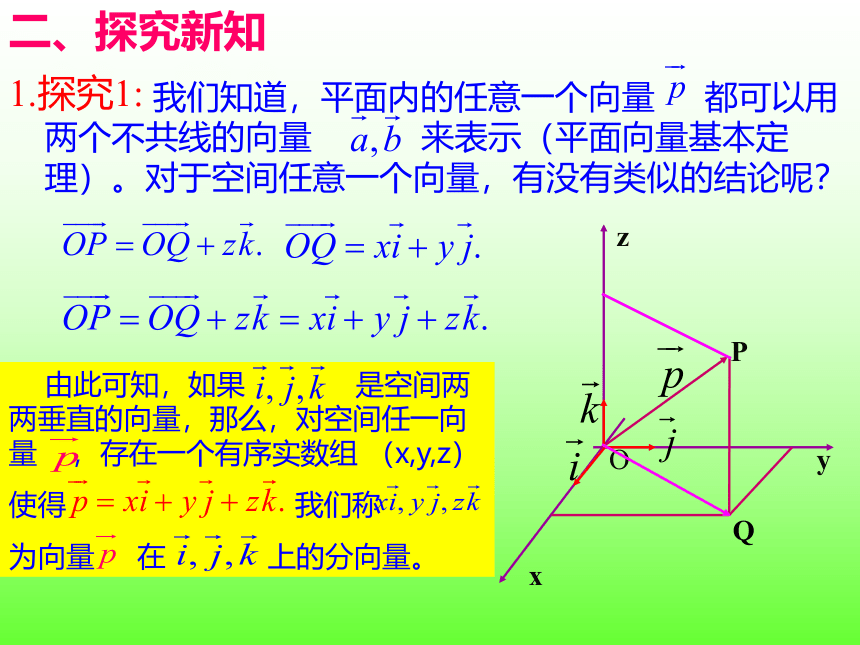
1.探究1:
我们知道,平面内的任意一个向量 都可以用两个不共线的向量 来表示(平面向量基本定理)。对于空间任意一个向量,有没有类似的结论呢?
x
y
z
O
Q
P
由此可知,如果 是空间两两垂直的向量,那么,对空间任一向量 ,存在一个有序实数组 (x,y,z)
使得 我们称
为向量 在 上的分向量。
二、探究新知
2.探究2:在空间中,如果用任意三个不共面向量
代替两两垂直的向量 , 你能得出类似的
结论吗?
任意不共面的三个向量都可做为空间的一个基底。
3.空间向量基本定理:
如果三个向量 不共面,那么对空间任一向量 ,存在一个唯一的有序实数组(x,y,z),使
都叫做基向量
(1)任意不共面的三个向量都可做为空间的一个基底。
特别提示:对于基底{a,b,c},除了应知道a,b,c不共面,
还应明确:
(2) 由于可视 为与任意一个非零向量共线,与任 意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是 。
(3)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念。
推论:设O、A、B、C是不共线的四点,则对空间任一 点P,都存在唯一的有序实数组( x,y,z),使
当且仅当 x+y+z=1 时,P、A、B、C四点共面。
1.巩固1. 已知向量 是空间的一个基底.
求证:向量 能构成空间的一个基底.
三、巩固新知
B
O
A
C
M
N
P
2.例1.
3.变式1:
O
A
B
C
M
N
B
B
O
A
C
P
N
M
Q
4.变式2:
已知平行六面体
5.变式3:
B
C
O
A1
B1
C1
O1
A
G
B
C
D
A1
B1
C1
D1
A
M
N
6.例2.
A′
B′
C′
D′
A
B
C
D
G
E
F
O
7.例3.
A′
B′
C′
D′
A
B
C
D
F
E
G
8.变式:
空间向量基本定理
都叫做基向量.
四、课堂小结
选好基底
第一章 统计案例
1.2
空间向量的基本定理
学习目标
1.理解空间向量基本定理;
2.理解基底、基向量及向量的坐标表示、正交分解的概念;
3.会用空间向量基本定理解决立体几何的简单问题.
4.核心素养:数学建模、数学运算。
1.平面向量基本定理:
2.平面向量的正交分解及坐标表示
x
y
o
一、回顾旧知
1.探究1:
我们知道,平面内的任意一个向量 都可以用两个不共线的向量 来表示(平面向量基本定理)。对于空间任意一个向量,有没有类似的结论呢?
x
y
z
O
Q
P
由此可知,如果 是空间两两垂直的向量,那么,对空间任一向量 ,存在一个有序实数组 (x,y,z)
使得 我们称
为向量 在 上的分向量。
二、探究新知
2.探究2:在空间中,如果用任意三个不共面向量
代替两两垂直的向量 , 你能得出类似的
结论吗?
任意不共面的三个向量都可做为空间的一个基底。
3.空间向量基本定理:
如果三个向量 不共面,那么对空间任一向量 ,存在一个唯一的有序实数组(x,y,z),使
都叫做基向量
(1)任意不共面的三个向量都可做为空间的一个基底。
特别提示:对于基底{a,b,c},除了应知道a,b,c不共面,
还应明确:
(2) 由于可视 为与任意一个非零向量共线,与任 意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是 。
(3)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念。
推论:设O、A、B、C是不共线的四点,则对空间任一 点P,都存在唯一的有序实数组( x,y,z),使
当且仅当 x+y+z=1 时,P、A、B、C四点共面。
1.巩固1. 已知向量 是空间的一个基底.
求证:向量 能构成空间的一个基底.
三、巩固新知
B
O
A
C
M
N
P
2.例1.
3.变式1:
O
A
B
C
M
N
B
B
O
A
C
P
N
M
Q
4.变式2:
已知平行六面体
5.变式3:
B
C
O
A1
B1
C1
O1
A
G
B
C
D
A1
B1
C1
D1
A
M
N
6.例2.
A′
B′
C′
D′
A
B
C
D
G
E
F
O
7.例3.
A′
B′
C′
D′
A
B
C
D
F
E
G
8.变式:
空间向量基本定理
都叫做基向量.
四、课堂小结
选好基底
