第22章 二次函数 单元综合水平检测试题 2023-2024学年人教版数学九年级上册(含答案)
文档属性
| 名称 | 第22章 二次函数 单元综合水平检测试题 2023-2024学年人教版数学九年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 615.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-19 15:54:21 | ||
图片预览

文档简介
2023-2024学年人教版数学九年级上册
第22章二次函数单元综合水平检测试题
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知是二次函数,则的值为( )
A. B. C. D. 或
2. 下列各式中,是的二次函数的是( )
A. B.
C. D.
3. 若函数则当函数值时,自变量的值是.( )
A. B. C. 或 D. 或
4. 已知二次函数,当时,随的增大而减小,则有( )
A. B. C. D.
5. 将抛物线向左平移个单位长度,再向下平移个单位长度,得到的抛物线的函数解析式为( )
A. B.
C. D.
6. 抛物线的顶点坐标是( )
A. B. C. D.
7. 抛物线过,,三点,则,,大小关系是( )
A. B. C. D.
8. 二次函数为常数,的部分图象如图所示,图象顶点的坐标为,与轴的一个交点在点和点之间,有下列结论:
;
;
;
;
为任意实数.
其中正确的有( )
A. 个 B. 个 C. 个 D. 个
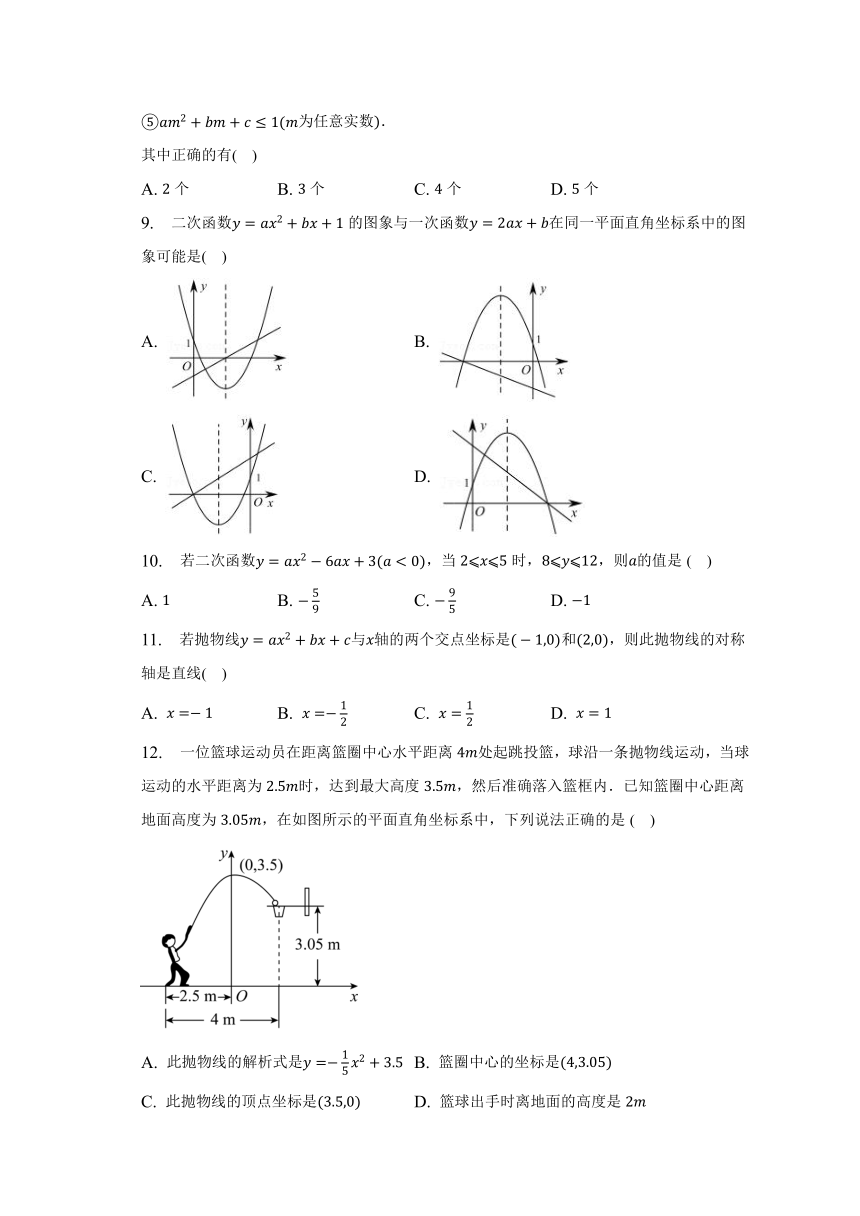
9. 二次函数的图象与一次函数在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
10. 若二次函数,当时,,则的值是( )
A. B. C. D.
11. 若抛物线与轴的两个交点坐标是和,则此抛物线的对称轴是直线( )
A. B. C. D.
12. 一位篮球运动员在距离篮圈中心水平距离处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为时,达到最大高度,然后准确落入篮框内.已知篮圈中心距离地面高度为,在如图所示的平面直角坐标系中,下列说法正确的是( )
A. 此抛物线的解析式是 B. 篮圈中心的坐标是
C. 此抛物线的顶点坐标是 D. 篮球出手时离地面的高度是
二、填空题(本大题共8小题,共24.0分)
13. 某工厂今年八月份医用防护服的产量是万件,计划九月份和十月份增加产量,如果月平均增长率为,那么十月份医用防护服的产量万件与之间的函数表达式为 .
14. 把二次函数化成形如的形式是 .
15. 将抛物线向下平移个单位长度后与轴的两个交点之间的距离为______.
16. 抛物线与轴的一个交点的坐标为,则代数式 .
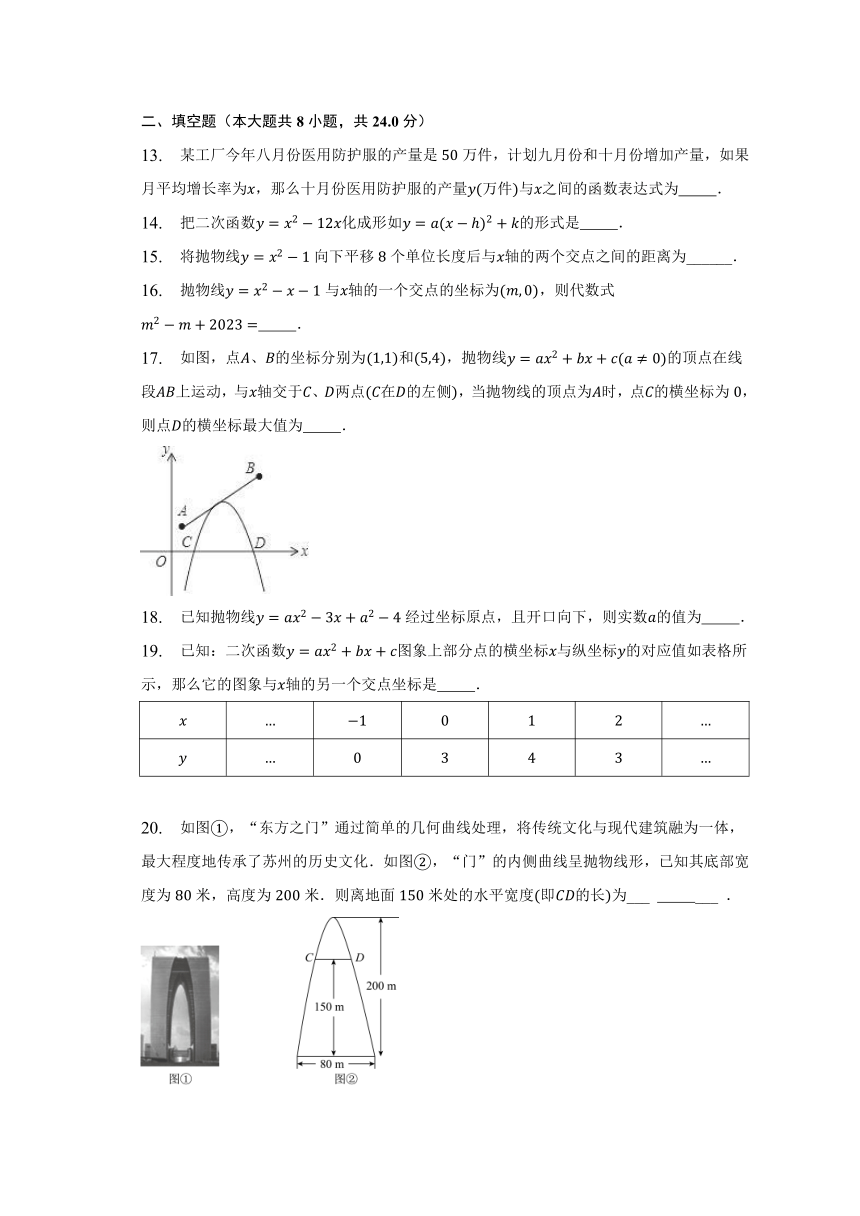
17. 如图,点、的坐标分别为和,抛物线的顶点在线段上运动,与轴交于、两点在的左侧,当抛物线的顶点为时,点的横坐标为,则点的横坐标最大值为 .
18. 已知抛物线经过坐标原点,且开口向下,则实数的值为 .
19. 已知:二次函数图象上部分点的横坐标与纵坐标的对应值如表格所示,那么它的图象与轴的另一个交点坐标是 .
20. 如图,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图,“门”的内侧曲线呈抛物线形,已知其底部宽度为米,高度为米.则离地面米处的水平宽度即的长为___ ___ .
三、解答题(本大题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤)
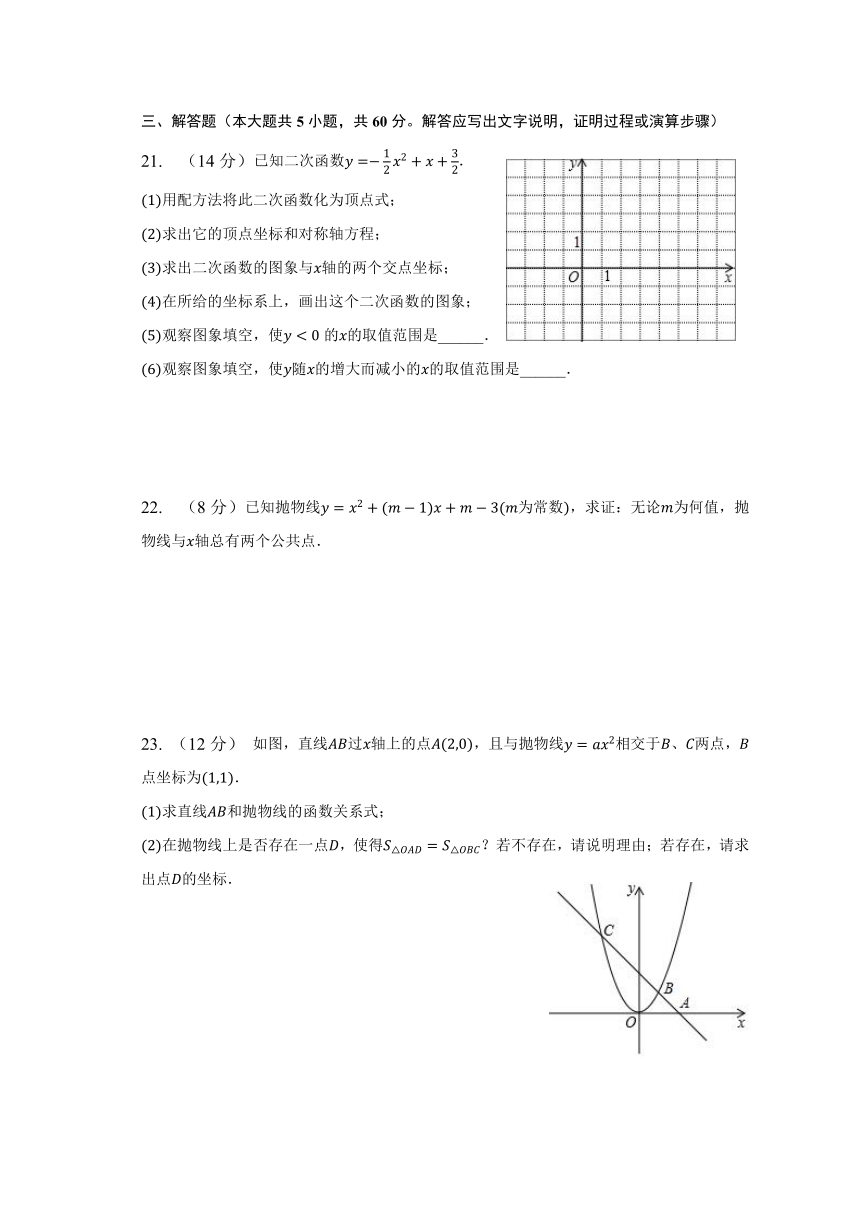
21. (14分)已知二次函数.
用配方法将此二次函数化为顶点式;
求出它的顶点坐标和对称轴方程;
求出二次函数的图象与轴的两个交点坐标;
在所给的坐标系上,画出这个二次函数的图象;
观察图象填空,使的的取值范围是______.
观察图象填空,使随的增大而减小的的取值范围是______.
22. (8分)已知抛物线为常数,求证:无论为何值,抛物线与轴总有两个公共点.
23. (12分) 如图,直线过轴上的点,且与抛物线相交于、两点,点坐标为.
求直线和抛物线的函数关系式;
在抛物线上是否存在一点,使得?若不存在,请说明理由;若存在,请求出点的坐标.
24. 本小题分
如图,抛物线与轴交于、两点,与轴交于点,点的坐标为
求的值及顶点的坐标;
点是抛物线对称轴上的一个动点,求的最小值.
本小题分
抖音直播带货的兴起,越来越多的商家都开启了抖音直播带货的模式某商家在直播间销售某种商品,每件售价为元,每周可卖件为了促销,商家决定降价销售,据市场大数据显示:销售单价每降价元,每周可多卖件,商品成本单价为元设商品销售单价为元,每周的销售量为件.
求与之间的函数关系式;
当销售单价定为多少时,每周销售该商品获利最大,最大利润是多少元?
若商家在销售该商品时每周想要获得不低于元的利润,每周至少要销售多少件?
第22章二次函数单元综合水平检测试题
参考答案
2. 3. 4. 5. 6.
7. 8. 9. 10. 11. 12.
13.
14.
15.
16.
17.
18.
19.
20. 米
21. 或
22. 证明:
,
无论为何值,抛物线与轴总有两个公共点.
23. 解:设直线关系式为,都在直线的图象上,
解得,
直线关系式为,
点在的图象上,
,其关系式为;
如图,存在点,设,
由题意得,
解得或,
,
,
,
,
解得,
点坐标为或.
24. 解:把代入得,解得,
抛物线解析式为,
,
抛物线的顶点坐标为.
抛物线的对称轴为直线,
当时,,则,
当时,,解得,,则,
连接交直线于,如图,则,
此时的值最小,
,
的最小值为.
25. 解:由题意可得,
,
即与之间的函数关系式是.
设利润为元,
由题意可得:,
当时,取得最大值,此时.
答:当销售单价定为元时,每周销售该商品获利最大,最大利润是元.
令,
则,
解得,,
,
该函数图象开口向下,对称轴为直线,
商家在销售该商品时每周想要获得不低于元的利润,每周至少要销售件.
答:商家在销售该商品时每周想要获得不低于元的利润,每周至少要销售件.
第22章二次函数单元综合水平检测试题
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知是二次函数,则的值为( )
A. B. C. D. 或
2. 下列各式中,是的二次函数的是( )
A. B.
C. D.
3. 若函数则当函数值时,自变量的值是.( )
A. B. C. 或 D. 或
4. 已知二次函数,当时,随的增大而减小,则有( )
A. B. C. D.
5. 将抛物线向左平移个单位长度,再向下平移个单位长度,得到的抛物线的函数解析式为( )
A. B.
C. D.
6. 抛物线的顶点坐标是( )
A. B. C. D.
7. 抛物线过,,三点,则,,大小关系是( )
A. B. C. D.
8. 二次函数为常数,的部分图象如图所示,图象顶点的坐标为,与轴的一个交点在点和点之间,有下列结论:
;
;
;
;
为任意实数.
其中正确的有( )
A. 个 B. 个 C. 个 D. 个
9. 二次函数的图象与一次函数在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
10. 若二次函数,当时,,则的值是( )
A. B. C. D.
11. 若抛物线与轴的两个交点坐标是和,则此抛物线的对称轴是直线( )
A. B. C. D.
12. 一位篮球运动员在距离篮圈中心水平距离处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为时,达到最大高度,然后准确落入篮框内.已知篮圈中心距离地面高度为,在如图所示的平面直角坐标系中,下列说法正确的是( )
A. 此抛物线的解析式是 B. 篮圈中心的坐标是
C. 此抛物线的顶点坐标是 D. 篮球出手时离地面的高度是
二、填空题(本大题共8小题,共24.0分)
13. 某工厂今年八月份医用防护服的产量是万件,计划九月份和十月份增加产量,如果月平均增长率为,那么十月份医用防护服的产量万件与之间的函数表达式为 .
14. 把二次函数化成形如的形式是 .
15. 将抛物线向下平移个单位长度后与轴的两个交点之间的距离为______.
16. 抛物线与轴的一个交点的坐标为,则代数式 .
17. 如图,点、的坐标分别为和,抛物线的顶点在线段上运动,与轴交于、两点在的左侧,当抛物线的顶点为时,点的横坐标为,则点的横坐标最大值为 .
18. 已知抛物线经过坐标原点,且开口向下,则实数的值为 .
19. 已知:二次函数图象上部分点的横坐标与纵坐标的对应值如表格所示,那么它的图象与轴的另一个交点坐标是 .
20. 如图,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图,“门”的内侧曲线呈抛物线形,已知其底部宽度为米,高度为米.则离地面米处的水平宽度即的长为___ ___ .
三、解答题(本大题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤)
21. (14分)已知二次函数.
用配方法将此二次函数化为顶点式;
求出它的顶点坐标和对称轴方程;
求出二次函数的图象与轴的两个交点坐标;
在所给的坐标系上,画出这个二次函数的图象;
观察图象填空,使的的取值范围是______.
观察图象填空,使随的增大而减小的的取值范围是______.
22. (8分)已知抛物线为常数,求证:无论为何值,抛物线与轴总有两个公共点.
23. (12分) 如图,直线过轴上的点,且与抛物线相交于、两点,点坐标为.
求直线和抛物线的函数关系式;
在抛物线上是否存在一点,使得?若不存在,请说明理由;若存在,请求出点的坐标.
24. 本小题分
如图,抛物线与轴交于、两点,与轴交于点,点的坐标为
求的值及顶点的坐标;
点是抛物线对称轴上的一个动点,求的最小值.
本小题分
抖音直播带货的兴起,越来越多的商家都开启了抖音直播带货的模式某商家在直播间销售某种商品,每件售价为元,每周可卖件为了促销,商家决定降价销售,据市场大数据显示:销售单价每降价元,每周可多卖件,商品成本单价为元设商品销售单价为元,每周的销售量为件.
求与之间的函数关系式;
当销售单价定为多少时,每周销售该商品获利最大,最大利润是多少元?
若商家在销售该商品时每周想要获得不低于元的利润,每周至少要销售多少件?
第22章二次函数单元综合水平检测试题
参考答案
2. 3. 4. 5. 6.
7. 8. 9. 10. 11. 12.
13.
14.
15.
16.
17.
18.
19.
20. 米
21. 或
22. 证明:
,
无论为何值,抛物线与轴总有两个公共点.
23. 解:设直线关系式为,都在直线的图象上,
解得,
直线关系式为,
点在的图象上,
,其关系式为;
如图,存在点,设,
由题意得,
解得或,
,
,
,
,
解得,
点坐标为或.
24. 解:把代入得,解得,
抛物线解析式为,
,
抛物线的顶点坐标为.
抛物线的对称轴为直线,
当时,,则,
当时,,解得,,则,
连接交直线于,如图,则,
此时的值最小,
,
的最小值为.
25. 解:由题意可得,
,
即与之间的函数关系式是.
设利润为元,
由题意可得:,
当时,取得最大值,此时.
答:当销售单价定为元时,每周销售该商品获利最大,最大利润是元.
令,
则,
解得,,
,
该函数图象开口向下,对称轴为直线,
商家在销售该商品时每周想要获得不低于元的利润,每周至少要销售件.
答:商家在销售该商品时每周想要获得不低于元的利润,每周至少要销售件.
同课章节目录
