切线的性质与判定(江苏省南通市如皋市)
文档属性
| 名称 | 切线的性质与判定(江苏省南通市如皋市) |

|
|
| 格式 | rar | ||
| 文件大小 | 141.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-12 00:00:00 | ||
图片预览

文档简介
袁桥镇中九年级数学学案 2007-09-19
24.2.2直线和圆的位置关系(1)
知识目标:1.理解直线和圆的位置关系2.掌握直线和圆的位置关系的数量关系定理
技能目标:通过直观演示,培养学生能从直观演示中归纳出几何性质的能力
情感目标:在用运动的观点揭示直线和圆的位置关系的过程中向学生渗透,世界上的
一切事物都是变化着的,并且在变化的过程中在一定的条件下是可以相互转化的.
重难点: 1. 正确理解直线和圆的位置关系,特别是直线和圆相切的关系
2. 直线和圆的位置关系与圆心到直线的距离和圆的半径大小关系的对应,
它既可做为各种位置关系的判定,又可作为性质.
教学过程:
1、 复习与提问
2、 动手探索,发现新知
1、媒体展示:太阳看成一个圆,地平线看成一条直线,
观察直线和圆的位置关系有几种,并给出相应的概念
2、类比点与圆的位置关系,给出直线与圆的位置关系的判定方法。
设d表示圆心O到直线l的距离(简称线心距),r表示⊙O的半径
则有⑴直线l和⊙O相交
⑵直线l和⊙O相切
⑶直线l和⊙O相离
3、归纳:直线与圆的位置关系判定方法:
直线和圆的位置关系 相交 相切 相离
公共点个数
圆心到直线距离 d 与半径 r 关系
公共点名称
直线名称
4、练习:P102页练习1 ,然后阅读 P102页思考
归纳切线的判定定理: 并且 的直线是圆的切线。
5、阅读课本P103页例1。
例2、如图所示,PA是的平分线,AB是⊙O的切线,切点E,
那么AC是⊙O的切线吗?为什么?
]
6、探索:圆O与直线l相切,则过点A的直径A B与切线l有
怎样的位置关系?
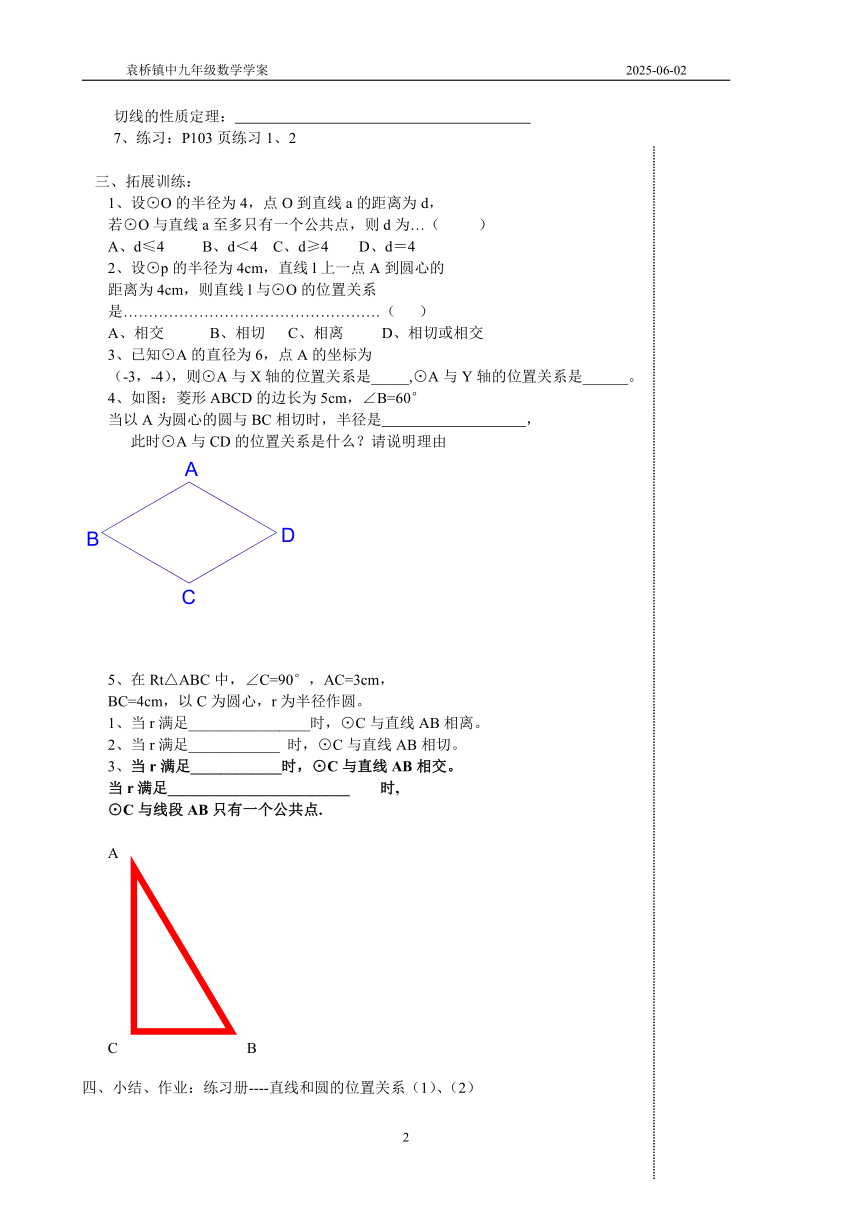
切线的性质定理:
7、练习:P103页练习1、2
3、 拓展训练:
1、设⊙O的半径为4,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d为…( )
A、d≤4 B、d<4 C、d≥4 D、d=4
2、设⊙p的半径为4cm,直线l上一点A到圆心的
距离为4cm,则直线l与⊙O的位置关系
是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交
3、已知⊙A的直径为6,点A的坐标为
(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。
4、如图:菱形ABCD的边长为5cm,∠B=60°
当以A为圆心的圆与BC相切时,半径是 ,
此时⊙A与CD的位置关系是什么?请说明理由
5、在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。
1、当r满足________________时,⊙C与直线AB相离。
2、当r满足____________ 时,⊙C与直线AB相切。
3、当r满足____________时,⊙C与直线AB相交。
当r满足________________________ 时,
⊙C与线段AB只有一个公共点.
A
C B
四、小结、作业:练习册----直线和圆的位置关系(1)、(2)
24.2.2直线和圆的位置关系(2)
知识目标:1.使学生理解切线长定义.2.使学生掌握切线长定理,并能初步运用.
技能目标:通过直观演示切线长,培养学生的语言表达能力.
通过对切线长定理的证明,培养学生对几何性质的归纳能力.
重难点:切线长定理,切线长定理的归纳与定理的应用。
教学过程:
1、 复习与提问
二、动手探索,发现新知
1、经过平面上的已知点作已知圆的切线,会有怎样的情形呢?请同学们打开
练习本画一画.
2、观察从圆外一点所引圆的切线上,有一条线段,线段的端点一边是已知点,
一边是 .(给出切线长概概念)
3、思考课本P104页的探究
4、归纳切线长定理:从圆外一点引圆的两条切线,它们的 相等,
这一点和圆心的连线平分 夹角.
5、例1、已知,如图,PA、PB是⊙O的两条切线,A、B为切点.直线 OP 交 ⊙O
于点 D、E,交 AB 于 C.
(1)写出图中所有的垂直关系;
(2)写出图中所有的全等三角形.
(3)如果 PA = 4 cm , PD = 2 cm , 求半径 OA 的长.
6、探索课本P104页的思考,阅读课本P105页例2前面的内容。
7、如图23.2.12,在△ABC中,如果有一圆与AB、AC、BC都相切,那么该圆的,
圆心到这三角形的三边的距离都相等,如何找到这个圆的圆心和半径呢?
8、概括: 与三角形各边都 的圆叫做三角形的内切圆,
三角形的内切圆的圆心叫做三角形的 ,
这个三角形叫做圆的 ,三角形的内心就是
三角形三条 的交点,它到三角形 距离相等。
问题:三角形的内切圆有几个?一个圆的外切三角形是否只有一个?
9、阅读课本P105页,例2
10、例2、已知:如图7-69,四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于
L、M、N,P.求证:AB+CD=AD+BC.
结论归纳:
学生练习:课本P106页练习
2、 拓展训练:
1、 已知:⊙O的半径为3厘米,点P和圆心O的距离为6厘米,经过
点P和⊙O的两条切线,求这两条切线的夹角为 ,切线长为 .
2、直角三角形的外接圆半径为5cm,内切圆半径为1cm,
则此三角形的周长是_______.
3、⊙O边长为2cm的正方形ABCD的内切圆,E、F切⊙O
于P点,交AB、BC于E、F,则△BEF的周长是_____.
4、已知:如图7-68,P为⊙O外一点,PA、PB为⊙O的切线,
A和B是切点,BC是直径.
求证:AC∥OP.
5、已知:三角形ABC内接于⊙O,过点A作直线EF.
(1)图甲,AB为直径,要使得EF是⊙O切线,还需添加的条件
(只需写出三种情况)①___________②_____________
③______________.
(2)图乙, AB为非直径的弦,∠CAE=∠B.求证:EF是⊙O的
切线.
四、小结、作业:练习册----直线和圆的位置关系(3)
_
P
_
O
_
C
_
B
_
A
PAGE
3
24.2.2直线和圆的位置关系(1)
知识目标:1.理解直线和圆的位置关系2.掌握直线和圆的位置关系的数量关系定理
技能目标:通过直观演示,培养学生能从直观演示中归纳出几何性质的能力
情感目标:在用运动的观点揭示直线和圆的位置关系的过程中向学生渗透,世界上的
一切事物都是变化着的,并且在变化的过程中在一定的条件下是可以相互转化的.
重难点: 1. 正确理解直线和圆的位置关系,特别是直线和圆相切的关系
2. 直线和圆的位置关系与圆心到直线的距离和圆的半径大小关系的对应,
它既可做为各种位置关系的判定,又可作为性质.
教学过程:
1、 复习与提问
2、 动手探索,发现新知
1、媒体展示:太阳看成一个圆,地平线看成一条直线,
观察直线和圆的位置关系有几种,并给出相应的概念
2、类比点与圆的位置关系,给出直线与圆的位置关系的判定方法。
设d表示圆心O到直线l的距离(简称线心距),r表示⊙O的半径
则有⑴直线l和⊙O相交
⑵直线l和⊙O相切
⑶直线l和⊙O相离
3、归纳:直线与圆的位置关系判定方法:
直线和圆的位置关系 相交 相切 相离
公共点个数
圆心到直线距离 d 与半径 r 关系
公共点名称
直线名称
4、练习:P102页练习1 ,然后阅读 P102页思考
归纳切线的判定定理: 并且 的直线是圆的切线。
5、阅读课本P103页例1。
例2、如图所示,PA是的平分线,AB是⊙O的切线,切点E,
那么AC是⊙O的切线吗?为什么?
]
6、探索:圆O与直线l相切,则过点A的直径A B与切线l有
怎样的位置关系?
切线的性质定理:
7、练习:P103页练习1、2
3、 拓展训练:
1、设⊙O的半径为4,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d为…( )
A、d≤4 B、d<4 C、d≥4 D、d=4
2、设⊙p的半径为4cm,直线l上一点A到圆心的
距离为4cm,则直线l与⊙O的位置关系
是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交
3、已知⊙A的直径为6,点A的坐标为
(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。
4、如图:菱形ABCD的边长为5cm,∠B=60°
当以A为圆心的圆与BC相切时,半径是 ,
此时⊙A与CD的位置关系是什么?请说明理由
5、在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。
1、当r满足________________时,⊙C与直线AB相离。
2、当r满足____________ 时,⊙C与直线AB相切。
3、当r满足____________时,⊙C与直线AB相交。
当r满足________________________ 时,
⊙C与线段AB只有一个公共点.
A
C B
四、小结、作业:练习册----直线和圆的位置关系(1)、(2)
24.2.2直线和圆的位置关系(2)
知识目标:1.使学生理解切线长定义.2.使学生掌握切线长定理,并能初步运用.
技能目标:通过直观演示切线长,培养学生的语言表达能力.
通过对切线长定理的证明,培养学生对几何性质的归纳能力.
重难点:切线长定理,切线长定理的归纳与定理的应用。
教学过程:
1、 复习与提问
二、动手探索,发现新知
1、经过平面上的已知点作已知圆的切线,会有怎样的情形呢?请同学们打开
练习本画一画.
2、观察从圆外一点所引圆的切线上,有一条线段,线段的端点一边是已知点,
一边是 .(给出切线长概概念)
3、思考课本P104页的探究
4、归纳切线长定理:从圆外一点引圆的两条切线,它们的 相等,
这一点和圆心的连线平分 夹角.
5、例1、已知,如图,PA、PB是⊙O的两条切线,A、B为切点.直线 OP 交 ⊙O
于点 D、E,交 AB 于 C.
(1)写出图中所有的垂直关系;
(2)写出图中所有的全等三角形.
(3)如果 PA = 4 cm , PD = 2 cm , 求半径 OA 的长.
6、探索课本P104页的思考,阅读课本P105页例2前面的内容。
7、如图23.2.12,在△ABC中,如果有一圆与AB、AC、BC都相切,那么该圆的,
圆心到这三角形的三边的距离都相等,如何找到这个圆的圆心和半径呢?
8、概括: 与三角形各边都 的圆叫做三角形的内切圆,
三角形的内切圆的圆心叫做三角形的 ,
这个三角形叫做圆的 ,三角形的内心就是
三角形三条 的交点,它到三角形 距离相等。
问题:三角形的内切圆有几个?一个圆的外切三角形是否只有一个?
9、阅读课本P105页,例2
10、例2、已知:如图7-69,四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于
L、M、N,P.求证:AB+CD=AD+BC.
结论归纳:
学生练习:课本P106页练习
2、 拓展训练:
1、 已知:⊙O的半径为3厘米,点P和圆心O的距离为6厘米,经过
点P和⊙O的两条切线,求这两条切线的夹角为 ,切线长为 .
2、直角三角形的外接圆半径为5cm,内切圆半径为1cm,
则此三角形的周长是_______.
3、⊙O边长为2cm的正方形ABCD的内切圆,E、F切⊙O
于P点,交AB、BC于E、F,则△BEF的周长是_____.
4、已知:如图7-68,P为⊙O外一点,PA、PB为⊙O的切线,
A和B是切点,BC是直径.
求证:AC∥OP.
5、已知:三角形ABC内接于⊙O,过点A作直线EF.
(1)图甲,AB为直径,要使得EF是⊙O切线,还需添加的条件
(只需写出三种情况)①___________②_____________
③______________.
(2)图乙, AB为非直径的弦,∠CAE=∠B.求证:EF是⊙O的
切线.
四、小结、作业:练习册----直线和圆的位置关系(3)
_
P
_
O
_
C
_
B
_
A
PAGE
3
同课章节目录
