19.4 线段的垂直平分线 同步练习 沪教版(上海)数学八年级第一学期(无答案)
文档属性
| 名称 | 19.4 线段的垂直平分线 同步练习 沪教版(上海)数学八年级第一学期(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 234.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-19 16:57:13 | ||
图片预览


文档简介
19.4 线段的垂直平分线
一、单选题
1.如图,点P是△ABC内的一点,若PB=PC,则( )
A.点P在∠ABC的平分线上 B.点P在∠ACB的平分线上
C.点P在边AB的垂直平分线上 D.点P在边BC的垂直平分线上
2.如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在( )的垂直平分线上;
A.AB B.AC C.BC D.不能确定
3.图中的尺规作图是作( )
A.线段的垂直平分线 B.一条线段等于已知线段
C.一个角等于已知角 D.角的平分线
4.如图,直线与交于点O,,下列结论中正确的是( )
A. B.
C.是的垂直平分线 D.点P在的垂直平分线上
5.如图,已知线段,分别以点A、B为圆心,大于的长为半径画弧,两弧交于点C和点D,作直线,在上取两点P、M,连接、、、,则下列结论一定正确的是( )
A. B. C. D.
6.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
A.20 B.22 C.14 D.16
7.到△ABC的三边距离相等的点是△ABC的( )
A.三边中线的交点 B.三条角平分线的交点 C.三边上高的交点 D.三边垂直平分线的交点
8.如图,已知,则下列说法中不一定正确的是( )
A. B. C. D.
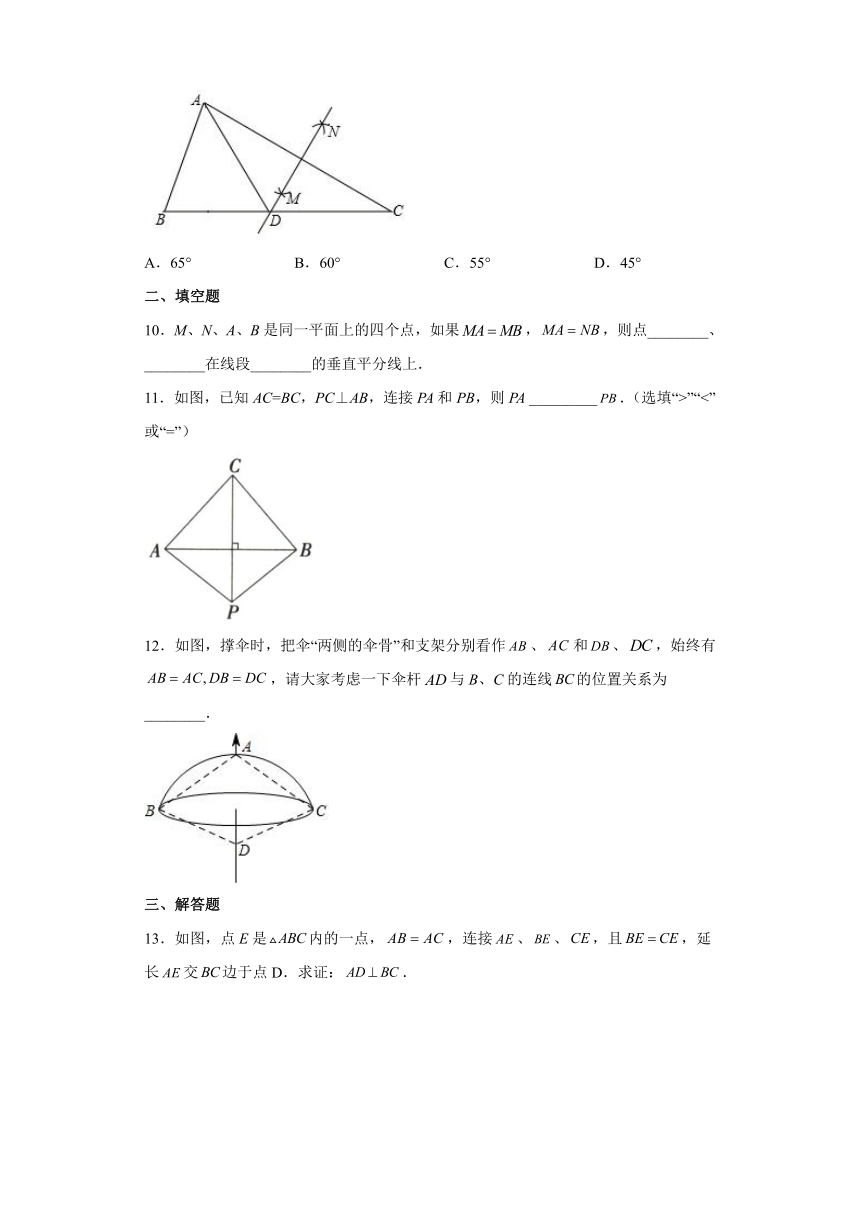
9.如图,△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N作直线MN,交BC于点D,连结AD,则∠BAD的度数为( )
A.65° B.60° C.55° D.45°
二、填空题
10.M、N、A、B是同一平面上的四个点,如果,,则点________、________在线段________的垂直平分线上.
11.如图,已知AC=BC,PC⊥AB,连接PA和PB,则PA _________.(选填“>”“<”或“=”)
12.如图,撑伞时,把伞“两侧的伞骨”和支架分别看作、和、,始终有,请大家考虑一下伞杆与B、C的连线的位置关系为________.
三、解答题
13.如图,点E是内的一点,,连接、、,且,延长交边于点D.求证:.
14.如图,在中,按以下步骤作图:①分别以点A、C为圆心,大于的长为半径画弧,两弧相交于M、N两点;②作直线交于点D,连接,若,求的度数.
15.(1)在△ABC中画出AB边的垂直平分线与BC边的垂直平分线.
(2)设所画的两条垂直平分线相交于点O,则由点O在AB的垂直平分线上,可以知道哪两条线段相等?
(3)由点O在BC的垂直平分线上,又可以得到什么结论?
(4)由(2)与(3)的结论,在线段的相等关系方面,你有什么新的发现?请先用等式表示,再用文字加以叙述.
16.尺规作图,在直线l上找一点P,使它到线段两端的距离相等,保留作图痕迹.
17.如图所示,为的角平分线,,求证:线段所在直线是线段的垂直平分线.
18.已知,如图,直线与直线相交于点,点是直线上一点.
求作:点,使直线,且点到、两点的距离相等(尺规作图,在题目的原图中完成作图)
19.已知:如图所示,在中,,点E在的垂直平分线上请问、、有何数量关系?并说明理由.
20.证明定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.已知:如图,A为线段外任意一点,且.求证:点A在的垂直平分线上.
21.如图,平面上的四边形是一只“风筝”的骨架,其中,某同学观察了这只“风筝”的骨架后,认为四边形的两条对角线,垂直,垂足为E,并且,你认为这位同学的判断正确吗?请说明理由.
22.如图,和关于直线对称,和关于直线对称.
(1)画出直线;
(2)直线与相交于点O,试探究与直线、所夹锐角的数量关系.
一、单选题
1.如图,点P是△ABC内的一点,若PB=PC,则( )
A.点P在∠ABC的平分线上 B.点P在∠ACB的平分线上
C.点P在边AB的垂直平分线上 D.点P在边BC的垂直平分线上
2.如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在( )的垂直平分线上;
A.AB B.AC C.BC D.不能确定
3.图中的尺规作图是作( )
A.线段的垂直平分线 B.一条线段等于已知线段
C.一个角等于已知角 D.角的平分线
4.如图,直线与交于点O,,下列结论中正确的是( )
A. B.
C.是的垂直平分线 D.点P在的垂直平分线上
5.如图,已知线段,分别以点A、B为圆心,大于的长为半径画弧,两弧交于点C和点D,作直线,在上取两点P、M,连接、、、,则下列结论一定正确的是( )
A. B. C. D.
6.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
A.20 B.22 C.14 D.16
7.到△ABC的三边距离相等的点是△ABC的( )
A.三边中线的交点 B.三条角平分线的交点 C.三边上高的交点 D.三边垂直平分线的交点
8.如图,已知,则下列说法中不一定正确的是( )
A. B. C. D.
9.如图,△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N作直线MN,交BC于点D,连结AD,则∠BAD的度数为( )
A.65° B.60° C.55° D.45°
二、填空题
10.M、N、A、B是同一平面上的四个点,如果,,则点________、________在线段________的垂直平分线上.
11.如图,已知AC=BC,PC⊥AB,连接PA和PB,则PA _________.(选填“>”“<”或“=”)
12.如图,撑伞时,把伞“两侧的伞骨”和支架分别看作、和、,始终有,请大家考虑一下伞杆与B、C的连线的位置关系为________.
三、解答题
13.如图,点E是内的一点,,连接、、,且,延长交边于点D.求证:.
14.如图,在中,按以下步骤作图:①分别以点A、C为圆心,大于的长为半径画弧,两弧相交于M、N两点;②作直线交于点D,连接,若,求的度数.
15.(1)在△ABC中画出AB边的垂直平分线与BC边的垂直平分线.
(2)设所画的两条垂直平分线相交于点O,则由点O在AB的垂直平分线上,可以知道哪两条线段相等?
(3)由点O在BC的垂直平分线上,又可以得到什么结论?
(4)由(2)与(3)的结论,在线段的相等关系方面,你有什么新的发现?请先用等式表示,再用文字加以叙述.
16.尺规作图,在直线l上找一点P,使它到线段两端的距离相等,保留作图痕迹.
17.如图所示,为的角平分线,,求证:线段所在直线是线段的垂直平分线.
18.已知,如图,直线与直线相交于点,点是直线上一点.
求作:点,使直线,且点到、两点的距离相等(尺规作图,在题目的原图中完成作图)
19.已知:如图所示,在中,,点E在的垂直平分线上请问、、有何数量关系?并说明理由.
20.证明定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.已知:如图,A为线段外任意一点,且.求证:点A在的垂直平分线上.
21.如图,平面上的四边形是一只“风筝”的骨架,其中,某同学观察了这只“风筝”的骨架后,认为四边形的两条对角线,垂直,垂足为E,并且,你认为这位同学的判断正确吗?请说明理由.
22.如图,和关于直线对称,和关于直线对称.
(1)画出直线;
(2)直线与相交于点O,试探究与直线、所夹锐角的数量关系.
