北师版八上数学 第一章 勾股定理 单元测试卷(含解析)
文档属性
| 名称 | 北师版八上数学 第一章 勾股定理 单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 321.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-19 18:53:59 | ||
图片预览



文档简介
北师版八上数学 第一章 勾股定理 单元测试卷
姓名:__________班级:__________考号:__________
、选择题(本大题共10小题,每小题3分,共15分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
下列由线段a、b、c组成的三角形,不是直角三角形的是( )
A. B.
C. D.
如图,已知正方形ABED与正方形BCFE,现从A,B,C,D,E,F六个点中任取三个点,使得这三个点能作为直角三角形的三个顶点,则这样的直角三角形共有( )
A.10 B.12 C.14 D.16
已知的三边长分别为5,13,12,则的面积为( )
A.30 B.60 C.78 D.不能确定
如果把直角三角形的两条直角边同时扩大到原来的2倍,那么斜边扩大到原来的( )
A. 1倍 B. 2倍 C. 3倍 D. 4倍
已知三角形的三边长为n、n+1、m(其中m2=2n+1),则此三角形( ).
A.一定是等边三角形 B.一定是等腰三角形
C.一定是直角三角形 D.形状无法确定
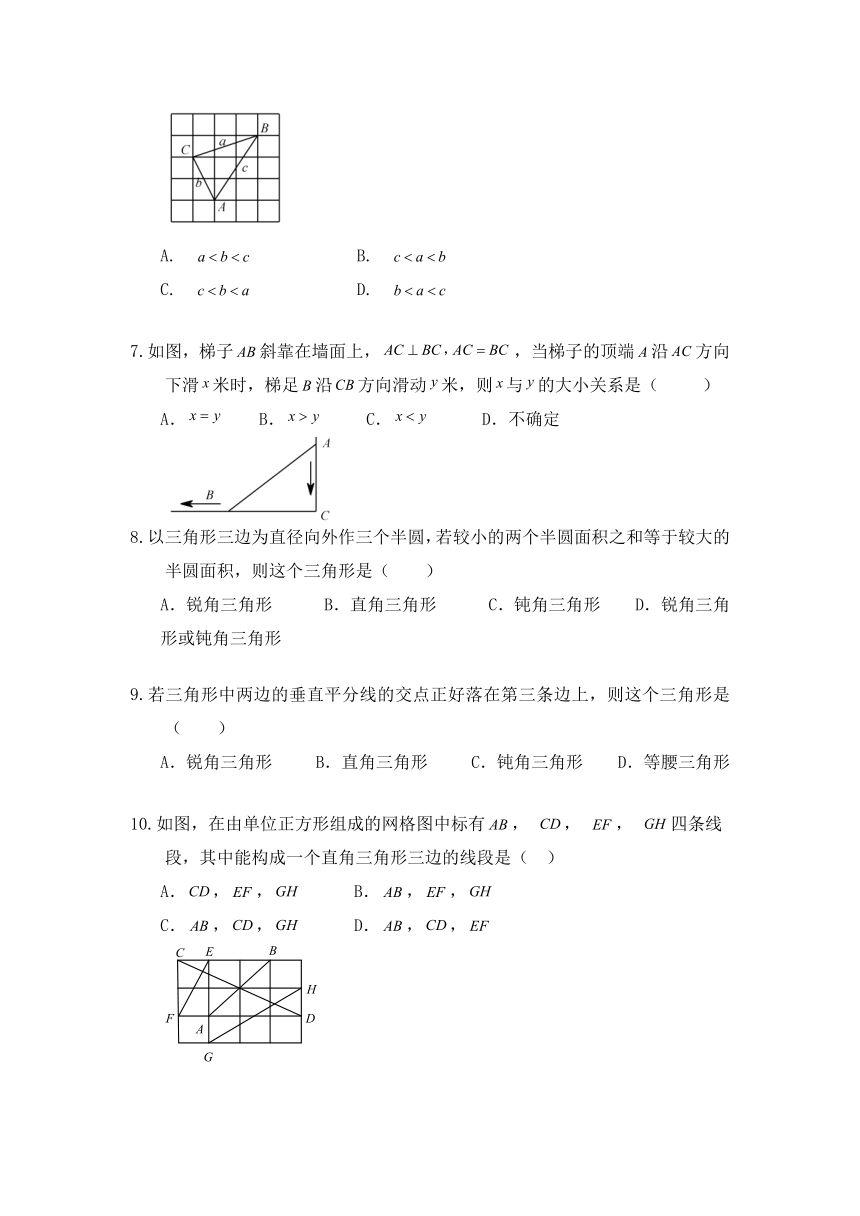
如图所示,在中,三边的大小关系是( )
A. B.
C. D.
如图,梯子斜靠在墙面上,,当梯子的顶端沿方向下滑米时,梯足沿方向滑动米,则与的大小关系是( )
A. B. C. D.不确定
以三角形三边为直径向外作三个半圆,若较小的两个半圆面积之和等于较大的半圆面积,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.锐角三角形或钝角三角形
若三角形中两边的垂直平分线的交点正好落在第三条边上,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
如图,在由单位正方形组成的网格图中标有, , , 四条线段,其中能构成一个直角三角形三边的线段是( )
A.,, B.,,
C.,, D.,,
、填空题(本大题共5小题,每小题3分,共15分)
如图,正方形网格中,每个小正方形的边长为1,则网格上的是______三角形.
ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边.
(1)若a=5,b=12,则c=______;
(2)若c=41,a=40,则b=______;
(3)若∠A=30°,a=1,则c=______,b=______;
(4)若∠A=45°,a=1,则b=______,c=______.
如图所示,在中,,且周长为36,点从点开始沿边向点以每秒1cm的速度移动;点从点沿边向点以每秒2cm的速度移动,如果同时出发,则过3秒时,的面积为 .
在RtABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,若c-a=4,b=16,则a、c分别为 .
已知的的对边分别是,且满足,则三角形的形状是 .
、解答题(本大题共7小题,共55分)
已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,
(1)如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,DEF是否仍为等腰直角三角形?证明你的结论.
如图,是垂直于地面的墙面,是一根斜靠在墙面上长为的木条,当木条端点沿墙面下滑时,沿地面向右滑行
⑴设木条的中点为,试判断木条滑行过程中,墙角处点到的距离怎样变化?说明理由
⑵木条在什么位置时,的面积最大?最大面积为多少?
如图,已知CA⊥AB,DB⊥AB,AC=BE,AE=BD.
(1)试猜想线段CE与DE的大小与位置关系,并说明你的结论;
(2)若AC=5,BD=12,求CE的长.
如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.
已知为的三边,且,试判断△ABC的形状.
阅读理解题:
(1)如图所示,在中,是边上的中线,且.求证:
(2)此题实际上是直角三角形的另一个判定定理,请你用文字语言叙述出来.
(3)直接运用这个结论解答下列题目:一个三角形一边长为2,这边上的中线长为1,另两边之和为,求这个三角形的面积.
如图,中,,,、为上的点,且,求证:.
北师版八上数学 第一章 勾股定理 单元测试卷北师版八上数学 第一章 勾股定理 单元测试卷答案解析
、选择题
1.D
2.C;可得到14个直角三角形,分别为、、
3.A;∵,∴三角形为直角三角形,
∵长为5,12的边为直角边,∴三角形的面积= 12×5×12=30.
4.B
5.C
6.D;= ,=,= . 选D.
7.B;由勾股定理得,化简得,
8.B;设最大半圆半径为c,最小半圆半径为a,第三个半圆半径为b,则三角形中最长边为2c,最短边长为2a,第三边为2b;∵较小的两个半圆面积之和等于较大的半圆面积,化简得:∴,符合勾股定理的逆定理,即三角形为直角三角形.
9.
10.B;,,,,选B.
、填空题
11.直角
12.(1)13;(2)9;(3)2,;(4)1,.
13. 18;设AB为3x,BC为4x,AC为5x,
∵周长为36,AB+BC+AC=36,∴3x+4x+5x=36得x=3∴AB=9,BC=12,AC=15
∵,∴是直角三角形
过3秒时,∴.
a=30,c=34
15.等腰直角三角形;因为,所以为等腰直角三角形
、解答题
16.(1)先连接AD,构造全等三角形:BED和AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:BED≌AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即DEF是等腰直角三角形;
(2)还是证明:BED≌AFD,主要证∠DAF=∠DBE(∠DBE=180°-45°=135°,∠DAF=90°+45°=135°),再结合两组对边对应相等,所以两个三角形全等.
17.⑴木条在滑行过程中,墙角处点到的距离保持不变,连结,因为木条在滑行过程中,始终是以为斜边的直角三角形,所以斜边上的中线
⑵设中边上的高为,则,在木条滑动的过程中,三角形的面积随的变化而变化,显然除与重合外,总有,即,当是等腰直角三角形时,与重合,取得最大值,这时三角形的面积最大,所以当木条与底面夹角为时,的面积最大,最大面积为
18.(1)易证△CAE∽△EBD,∴∠CEA+∠BED=∠CEA+∠ACE=90°,∴∠CED=90°,∴CE⊥DE
(2)由(1)可知AC=5,AE=BD=12,∴CE=13
19.EC=3cm;设EC=x,则DE=EF=8-x,AF=AD=10,BF=,CF=4.在中(8-x)2=x2+42,解得x=3
20.∵∴①
∵∴ ②
∵∴ ③
∵①+②得,①-③得
∴∴ABC是直角三角形.
21.(1)∵BD=CD,AD=BC,∴AD=BD=DC,
∴∠B=∠BAD,∠C=∠CAD,∵∠B+∠BAD+∠CAD+∠C=180°,
∴∠BAD+∠CAD=90°,即∠BAC=90°.
(2)根据题意用语言表述为:如果三角形斜边上的中线等于斜边的一半,那么这个三角形是直角 三角形.
(3)因为一个三角形一边长为2,这边上的中线长为1,所以这个三角形为直角三角形,
又∵∴,,
即,∴直角三角形的面积可得.
22.过点作线段,使,且.
在和中,
∴
∴,
在和中,
∴
∴
在中,,∴.
姓名:__________班级:__________考号:__________
、选择题(本大题共10小题,每小题3分,共15分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
下列由线段a、b、c组成的三角形,不是直角三角形的是( )
A. B.
C. D.
如图,已知正方形ABED与正方形BCFE,现从A,B,C,D,E,F六个点中任取三个点,使得这三个点能作为直角三角形的三个顶点,则这样的直角三角形共有( )
A.10 B.12 C.14 D.16
已知的三边长分别为5,13,12,则的面积为( )
A.30 B.60 C.78 D.不能确定
如果把直角三角形的两条直角边同时扩大到原来的2倍,那么斜边扩大到原来的( )
A. 1倍 B. 2倍 C. 3倍 D. 4倍
已知三角形的三边长为n、n+1、m(其中m2=2n+1),则此三角形( ).
A.一定是等边三角形 B.一定是等腰三角形
C.一定是直角三角形 D.形状无法确定
如图所示,在中,三边的大小关系是( )
A. B.
C. D.
如图,梯子斜靠在墙面上,,当梯子的顶端沿方向下滑米时,梯足沿方向滑动米,则与的大小关系是( )
A. B. C. D.不确定
以三角形三边为直径向外作三个半圆,若较小的两个半圆面积之和等于较大的半圆面积,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.锐角三角形或钝角三角形
若三角形中两边的垂直平分线的交点正好落在第三条边上,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
如图,在由单位正方形组成的网格图中标有, , , 四条线段,其中能构成一个直角三角形三边的线段是( )
A.,, B.,,
C.,, D.,,
、填空题(本大题共5小题,每小题3分,共15分)
如图,正方形网格中,每个小正方形的边长为1,则网格上的是______三角形.
ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边.
(1)若a=5,b=12,则c=______;
(2)若c=41,a=40,则b=______;
(3)若∠A=30°,a=1,则c=______,b=______;
(4)若∠A=45°,a=1,则b=______,c=______.
如图所示,在中,,且周长为36,点从点开始沿边向点以每秒1cm的速度移动;点从点沿边向点以每秒2cm的速度移动,如果同时出发,则过3秒时,的面积为 .
在RtABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,若c-a=4,b=16,则a、c分别为 .
已知的的对边分别是,且满足,则三角形的形状是 .
、解答题(本大题共7小题,共55分)
已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,
(1)如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,DEF是否仍为等腰直角三角形?证明你的结论.
如图,是垂直于地面的墙面,是一根斜靠在墙面上长为的木条,当木条端点沿墙面下滑时,沿地面向右滑行
⑴设木条的中点为,试判断木条滑行过程中,墙角处点到的距离怎样变化?说明理由
⑵木条在什么位置时,的面积最大?最大面积为多少?
如图,已知CA⊥AB,DB⊥AB,AC=BE,AE=BD.
(1)试猜想线段CE与DE的大小与位置关系,并说明你的结论;
(2)若AC=5,BD=12,求CE的长.
如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.
已知为的三边,且,试判断△ABC的形状.
阅读理解题:
(1)如图所示,在中,是边上的中线,且.求证:
(2)此题实际上是直角三角形的另一个判定定理,请你用文字语言叙述出来.
(3)直接运用这个结论解答下列题目:一个三角形一边长为2,这边上的中线长为1,另两边之和为,求这个三角形的面积.
如图,中,,,、为上的点,且,求证:.
北师版八上数学 第一章 勾股定理 单元测试卷北师版八上数学 第一章 勾股定理 单元测试卷答案解析
、选择题
1.D
2.C;可得到14个直角三角形,分别为、、
3.A;∵,∴三角形为直角三角形,
∵长为5,12的边为直角边,∴三角形的面积= 12×5×12=30.
4.B
5.C
6.D;= ,=,= . 选D.
7.B;由勾股定理得,化简得,
8.B;设最大半圆半径为c,最小半圆半径为a,第三个半圆半径为b,则三角形中最长边为2c,最短边长为2a,第三边为2b;∵较小的两个半圆面积之和等于较大的半圆面积,化简得:∴,符合勾股定理的逆定理,即三角形为直角三角形.
9.
10.B;,,,,选B.
、填空题
11.直角
12.(1)13;(2)9;(3)2,;(4)1,.
13. 18;设AB为3x,BC为4x,AC为5x,
∵周长为36,AB+BC+AC=36,∴3x+4x+5x=36得x=3∴AB=9,BC=12,AC=15
∵,∴是直角三角形
过3秒时,∴.
a=30,c=34
15.等腰直角三角形;因为,所以为等腰直角三角形
、解答题
16.(1)先连接AD,构造全等三角形:BED和AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:BED≌AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即DEF是等腰直角三角形;
(2)还是证明:BED≌AFD,主要证∠DAF=∠DBE(∠DBE=180°-45°=135°,∠DAF=90°+45°=135°),再结合两组对边对应相等,所以两个三角形全等.
17.⑴木条在滑行过程中,墙角处点到的距离保持不变,连结,因为木条在滑行过程中,始终是以为斜边的直角三角形,所以斜边上的中线
⑵设中边上的高为,则,在木条滑动的过程中,三角形的面积随的变化而变化,显然除与重合外,总有,即,当是等腰直角三角形时,与重合,取得最大值,这时三角形的面积最大,所以当木条与底面夹角为时,的面积最大,最大面积为
18.(1)易证△CAE∽△EBD,∴∠CEA+∠BED=∠CEA+∠ACE=90°,∴∠CED=90°,∴CE⊥DE
(2)由(1)可知AC=5,AE=BD=12,∴CE=13
19.EC=3cm;设EC=x,则DE=EF=8-x,AF=AD=10,BF=,CF=4.在中(8-x)2=x2+42,解得x=3
20.∵∴①
∵∴ ②
∵∴ ③
∵①+②得,①-③得
∴∴ABC是直角三角形.
21.(1)∵BD=CD,AD=BC,∴AD=BD=DC,
∴∠B=∠BAD,∠C=∠CAD,∵∠B+∠BAD+∠CAD+∠C=180°,
∴∠BAD+∠CAD=90°,即∠BAC=90°.
(2)根据题意用语言表述为:如果三角形斜边上的中线等于斜边的一半,那么这个三角形是直角 三角形.
(3)因为一个三角形一边长为2,这边上的中线长为1,所以这个三角形为直角三角形,
又∵∴,,
即,∴直角三角形的面积可得.
22.过点作线段,使,且.
在和中,
∴
∴,
在和中,
∴
∴
在中,,∴.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
