北师版八上数学 第一章 勾股定理 单元测试卷(含答案)
文档属性
| 名称 | 北师版八上数学 第一章 勾股定理 单元测试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 324.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-19 18:56:09 | ||
图片预览

文档简介
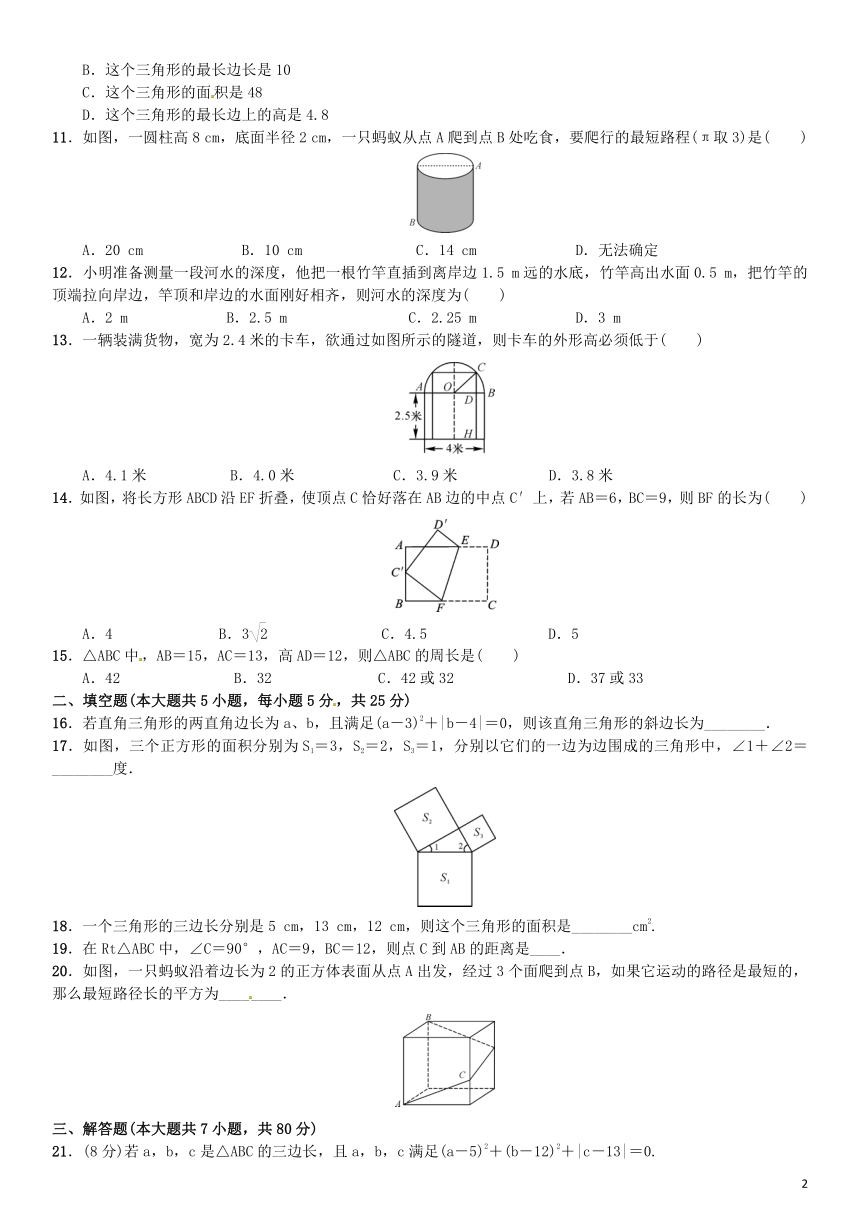
北师版八上数学 第一章 勾股定理 单元测试卷
(时间:120分钟 满分:150分)
一、选择题(本大题共15小题,每小题3分,共45分)
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
答案
1.一个直角三角形的两条直角边的长分别为6和8,则斜边长为( )
A. B. C.10 D.100
2.小明在一个长方形的水池里游泳,长方形的长、宽分别为30米、40米,小明在水池中沿直线最远可以游( )
A.30米 B.40米 C.50米 D.60米
3.下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )
A.3、4、5 B.6、8、10
C.4、6、9 D.5、12、13
4.将直角三角形的三边长同时扩大2倍,得到的三角形是( )
A.钝角三角形 B.锐角三角形
C.直角三角形 D.等腰三角形
5.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
6.在三角形ABC中,AB=8,AC=15,BC=17,则该三角形为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
7.暑假期间,小明的妈妈趁电器打价格战之机在网上购买了一台电视,小明量了电视机的屏幕后,发现屏幕长93厘米,宽52厘米,则这台电视机为______英寸(实际测量的误差可不计)( )
A.32(81厘米) B.39(99厘米)
C.42(106厘米) D.46(117厘米)
8.如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好与点C重合.若BC=5,CD=3,则BD的长为( )
A.1 B.2 C.3 D.4
9.如图,两个较大正方形的面积分别为225,289,则字母A所代表的正方形的面积为( )
A.4 B.8 C.16 D.64
10.已知a,b,c是三角形的三边长,如果满足(a-6)2++=0,那么下列说法中不正确的是( )
A.这个三角形是直角三角形
B.这个三角形的最长边长是10
C.这个三角形的面积是48
D.这个三角形的最长边上的高是4.8
11.如图,一圆柱高8 cm,底面半径2 cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( )
A.20 cm B.10 cm C.14 cm D.无法确定
12.小明准备测量一段河水的深度,他把一根竹竿直插到离岸边1.5 m远的水底,竹竿高出水面0.5 m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A.2 m B.2.5 m C.2.25 m D.3 m
13.一辆装满货物,宽为2.4米的卡车,欲通过如图所示的隧道,则卡车的外形高必须低于( )
A.4.1米 B.4.0米 C.3.9米 D.3.8米
14.如图,将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,若AB=6,BC=9,则BF的长为( )
A.4 B.3 C.4.5 D.5
15.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是( )
A.42 B.32 C.42或32 D.37或33
二、填空题(本大题共5小题,每小题5分,共25分)
16.若直角三角形的两直角边长为a、b,且满足(a-3)2+|b-4|=0,则该直角三角形的斜边长为________.
17.如图,三个正方形的面积分别为S1=3,S2=2,S3=1,分别以它们的一边为边围成的三角形中,∠1+∠2=________度.
18.一个三角形的三边长分别是5 cm,13 cm,12 cm,则这个三角形的面积是________cm2.
19.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是____.
20.如图,一只蚂蚁沿着边长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,那么最短路径长的平方为________.
三、解答题(本大题共7小题,共80分)
21.(8分)若a,b,c是△ABC的三边长,且a,b,c满足(a-5)2+(b-12)2+|c-13|=0.
(1)求a,b,c的值;
(2)△ABC是直角三角形吗?请说明理由.
22.(8分)飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4 000 米处,过了 20 秒,飞机距离这个男孩头顶5 000米,飞机每小时飞行多少千米?
23.(10分)如图,CD是AB上的高,AC=4,BC=3,BD= ,求AD2.
24.(12分)如图,有一个直角三角形纸片,两直角边AC=6 cm,BC=8 cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
25.(12分)如图,已知,在△ABC中,CD⊥AB于D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.
26.(14分)学校要征收一块土地,形状如图所示,∠B=∠D=90°,AB=20 m,BC=15 m,CD=7 m,土地价格为1 000元/m2,请你计算学校征收这块地需要多少钱?
27.(16分)如图,南北向MN为我国领海线,即MN以西为我国领海,以东为公海,上午9时50分,我国反走私艇A发现正东方有一走私艇以13海里/时的速度偷偷向我国领海开来,便立即通知正在MN线上巡逻的我国反走私艇B密切注意.反走私艇A和走私艇C的距离是13海里,A、B两艇的距离是5海里;反走私艇B测得距离C艇12海里,若走私艇C的速度不变,最早会在什么时候进入我国领海?
参考答案
1.C 2.C 3.C 4.C 5.A 6.B 7.C 8.D 9.D 10.C
11.B 12.A 13.A 14.A 15.C 16.5 17.90 18.30 19. 20.40
21.(1)由题意得a-5=0,b-12=0,c-13=0,所以a=5,b=12,c=13.(2)△ABC是直角三角形,理由:因为a2+b2=52+122=25+144=169,c2=132=169,所以a2+b2=c2.所以△ABC是直角三角形.
22.飞机每小时飞行540千米.
23.∵CD是AB上的高,∴△ADC和△BDC都是直角三角形. ∵在Rt△BDC中,BC=3,BD=, ∴CD2=BC2-BD2=32-=. ∵在Rt△ADC中,AC=4,CD2=, ∴AD2=AC2-CD2=42-=16-=.
24.设CD=x cm.在Rt△ABC中,AC=6 cm,BC=8 cm.由勾股定理得:AB2=BC2+AC2=100.所以AB=10 cm.由折叠可知:CD=DE,∠DEA=∠C=90°,AE=AC=6,所以∠BED=90°,BE=4.在Rt△BDE中,由勾股定理得:x2+42=(8-x)2,解得x=3.所以CD的长为3 cm.
25.(1)在△BCD中,因为CD⊥AB,所以BD2+CD2=BC2.所以CD2=BC2-BD2=152-92=144.所以CD=12.(2)在△ACD中,因为CD⊥AB,所以CD2+AD2=AC2.所以AD2=AC2-CD2=202-122=256.所以AD=16.所以AB=AD+BD=16+9=25.(3)因为BC2+AC2=152+202=625,AB2=252=625,所以AB2=BC2+AC2.所以△ABC是直角三角形.
26.连接AC.在△ABC中,∠B=90°,AB=20,BC=15,由勾股定理得:AC2=AB2+BC2=202+152=625.在△ADC中,∠D=90°,CD=7,由勾股定理得:AD2=AC2-CD2=625-72=576,AD=24.所以四边形的面积为:AB·BC+CD·AD=234(m2).234×1 000=234 000(元).答:学校征收这块地需要234 000元.
27.设MN与AC相交于点E,则∠BEC=90°.因为AB2+BC2=52+122=132=AC2,所以△ABC为直角三角形,且∠ABC=90°.由于MN⊥CE,所以走私艇C进入我国领海的最近的距离是CE.因为AB·BC=AC·BE=S△ABC,所以BE=.由勾股定理得CE2+BE2=BC2,解得CE=.÷13=≈0.85(h)=51(min).9时50分+51分=10时41分,即走私艇C最早会在10时41分进入我国领海.
PAGE
1
(时间:120分钟 满分:150分)
一、选择题(本大题共15小题,每小题3分,共45分)
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
答案
1.一个直角三角形的两条直角边的长分别为6和8,则斜边长为( )
A. B. C.10 D.100
2.小明在一个长方形的水池里游泳,长方形的长、宽分别为30米、40米,小明在水池中沿直线最远可以游( )
A.30米 B.40米 C.50米 D.60米
3.下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )
A.3、4、5 B.6、8、10
C.4、6、9 D.5、12、13
4.将直角三角形的三边长同时扩大2倍,得到的三角形是( )
A.钝角三角形 B.锐角三角形
C.直角三角形 D.等腰三角形
5.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
6.在三角形ABC中,AB=8,AC=15,BC=17,则该三角形为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
7.暑假期间,小明的妈妈趁电器打价格战之机在网上购买了一台电视,小明量了电视机的屏幕后,发现屏幕长93厘米,宽52厘米,则这台电视机为______英寸(实际测量的误差可不计)( )
A.32(81厘米) B.39(99厘米)
C.42(106厘米) D.46(117厘米)
8.如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好与点C重合.若BC=5,CD=3,则BD的长为( )
A.1 B.2 C.3 D.4
9.如图,两个较大正方形的面积分别为225,289,则字母A所代表的正方形的面积为( )
A.4 B.8 C.16 D.64
10.已知a,b,c是三角形的三边长,如果满足(a-6)2++=0,那么下列说法中不正确的是( )
A.这个三角形是直角三角形
B.这个三角形的最长边长是10
C.这个三角形的面积是48
D.这个三角形的最长边上的高是4.8
11.如图,一圆柱高8 cm,底面半径2 cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( )
A.20 cm B.10 cm C.14 cm D.无法确定
12.小明准备测量一段河水的深度,他把一根竹竿直插到离岸边1.5 m远的水底,竹竿高出水面0.5 m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A.2 m B.2.5 m C.2.25 m D.3 m
13.一辆装满货物,宽为2.4米的卡车,欲通过如图所示的隧道,则卡车的外形高必须低于( )
A.4.1米 B.4.0米 C.3.9米 D.3.8米
14.如图,将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,若AB=6,BC=9,则BF的长为( )
A.4 B.3 C.4.5 D.5
15.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是( )
A.42 B.32 C.42或32 D.37或33
二、填空题(本大题共5小题,每小题5分,共25分)
16.若直角三角形的两直角边长为a、b,且满足(a-3)2+|b-4|=0,则该直角三角形的斜边长为________.
17.如图,三个正方形的面积分别为S1=3,S2=2,S3=1,分别以它们的一边为边围成的三角形中,∠1+∠2=________度.
18.一个三角形的三边长分别是5 cm,13 cm,12 cm,则这个三角形的面积是________cm2.
19.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是____.
20.如图,一只蚂蚁沿着边长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,那么最短路径长的平方为________.
三、解答题(本大题共7小题,共80分)
21.(8分)若a,b,c是△ABC的三边长,且a,b,c满足(a-5)2+(b-12)2+|c-13|=0.
(1)求a,b,c的值;
(2)△ABC是直角三角形吗?请说明理由.
22.(8分)飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4 000 米处,过了 20 秒,飞机距离这个男孩头顶5 000米,飞机每小时飞行多少千米?
23.(10分)如图,CD是AB上的高,AC=4,BC=3,BD= ,求AD2.
24.(12分)如图,有一个直角三角形纸片,两直角边AC=6 cm,BC=8 cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
25.(12分)如图,已知,在△ABC中,CD⊥AB于D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.
26.(14分)学校要征收一块土地,形状如图所示,∠B=∠D=90°,AB=20 m,BC=15 m,CD=7 m,土地价格为1 000元/m2,请你计算学校征收这块地需要多少钱?
27.(16分)如图,南北向MN为我国领海线,即MN以西为我国领海,以东为公海,上午9时50分,我国反走私艇A发现正东方有一走私艇以13海里/时的速度偷偷向我国领海开来,便立即通知正在MN线上巡逻的我国反走私艇B密切注意.反走私艇A和走私艇C的距离是13海里,A、B两艇的距离是5海里;反走私艇B测得距离C艇12海里,若走私艇C的速度不变,最早会在什么时候进入我国领海?
参考答案
1.C 2.C 3.C 4.C 5.A 6.B 7.C 8.D 9.D 10.C
11.B 12.A 13.A 14.A 15.C 16.5 17.90 18.30 19. 20.40
21.(1)由题意得a-5=0,b-12=0,c-13=0,所以a=5,b=12,c=13.(2)△ABC是直角三角形,理由:因为a2+b2=52+122=25+144=169,c2=132=169,所以a2+b2=c2.所以△ABC是直角三角形.
22.飞机每小时飞行540千米.
23.∵CD是AB上的高,∴△ADC和△BDC都是直角三角形. ∵在Rt△BDC中,BC=3,BD=, ∴CD2=BC2-BD2=32-=. ∵在Rt△ADC中,AC=4,CD2=, ∴AD2=AC2-CD2=42-=16-=.
24.设CD=x cm.在Rt△ABC中,AC=6 cm,BC=8 cm.由勾股定理得:AB2=BC2+AC2=100.所以AB=10 cm.由折叠可知:CD=DE,∠DEA=∠C=90°,AE=AC=6,所以∠BED=90°,BE=4.在Rt△BDE中,由勾股定理得:x2+42=(8-x)2,解得x=3.所以CD的长为3 cm.
25.(1)在△BCD中,因为CD⊥AB,所以BD2+CD2=BC2.所以CD2=BC2-BD2=152-92=144.所以CD=12.(2)在△ACD中,因为CD⊥AB,所以CD2+AD2=AC2.所以AD2=AC2-CD2=202-122=256.所以AD=16.所以AB=AD+BD=16+9=25.(3)因为BC2+AC2=152+202=625,AB2=252=625,所以AB2=BC2+AC2.所以△ABC是直角三角形.
26.连接AC.在△ABC中,∠B=90°,AB=20,BC=15,由勾股定理得:AC2=AB2+BC2=202+152=625.在△ADC中,∠D=90°,CD=7,由勾股定理得:AD2=AC2-CD2=625-72=576,AD=24.所以四边形的面积为:AB·BC+CD·AD=234(m2).234×1 000=234 000(元).答:学校征收这块地需要234 000元.
27.设MN与AC相交于点E,则∠BEC=90°.因为AB2+BC2=52+122=132=AC2,所以△ABC为直角三角形,且∠ABC=90°.由于MN⊥CE,所以走私艇C进入我国领海的最近的距离是CE.因为AB·BC=AC·BE=S△ABC,所以BE=.由勾股定理得CE2+BE2=BC2,解得CE=.÷13=≈0.85(h)=51(min).9时50分+51分=10时41分,即走私艇C最早会在10时41分进入我国领海.
PAGE
1
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
