华师大版数学八年级下册17.3.4求一次函数的表达式 课件(共16张PPT)
文档属性
| 名称 | 华师大版数学八年级下册17.3.4求一次函数的表达式 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 195.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-19 18:58:48 | ||
图片预览





文档简介
(共16张PPT)
求一次函数的表达式
教材版本: 2013年华东师范大学出版社 学段学科: 初中数学
年级学期: 八年级 下册
问题1 前面,我们学习了一次函数及其图象和性
质,你还记得一次函数的一般解析式吗?
思考:
反过来已知一个一次函数的图象经过两个具体的点,
你能求出它的解析式吗?
两点法——两点确定一条直线
一、复习引入
问题2 你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
(k≠0)
设所求函数的表达式为_______________,
解:
y=kx+b(k≠0)
根据题意,得
10k+b=10
50k+b=18
解得,
k=0.2
b=8
∴所求函数表达式为 y= 0.2x +8(-20≤x≤100))
问题:温度计中水银(或酒精)柱的高度y(厘米)是温度x(℃)的一次函数。某种型号的实验用水银温度计能测量-20℃至100℃的温度,已知10℃时水银柱高10厘米,50℃时水银柱高18厘米。求这个函数的表达式。
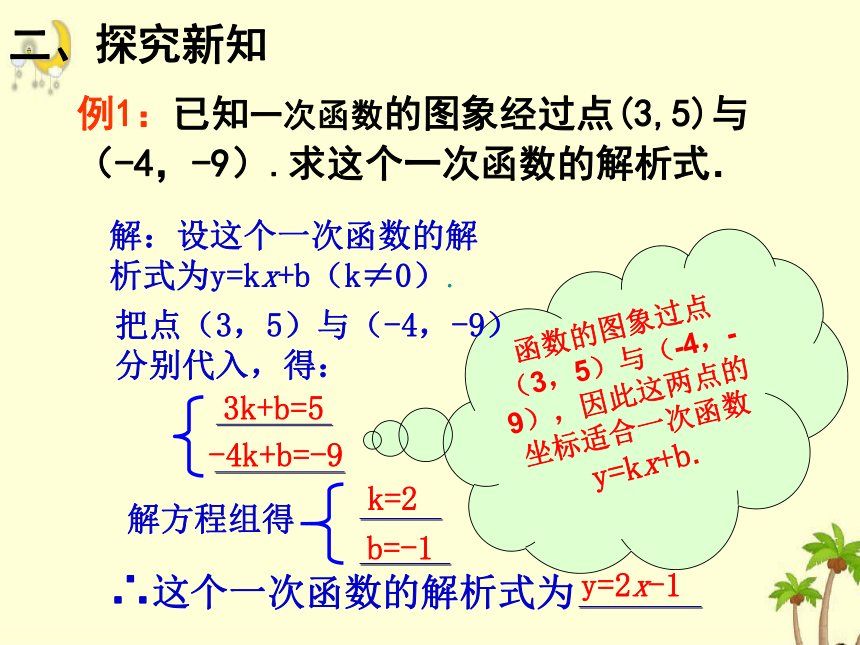
例1:已知一次函数的图象经过点(3,5)与
(-4,-9).求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b(k≠0).
3k+b=5
∴这个一次函数的解析式为
二、探究新知
函数的图象过点
(3,5)与(-4,-9),因此这两点的坐标适合一次函数y=kx+b.
解方程组得
把点(3,5)与(-4,-9)分别代入,得:
k=2
y=2x-1
b=-1
-4k+b=-9
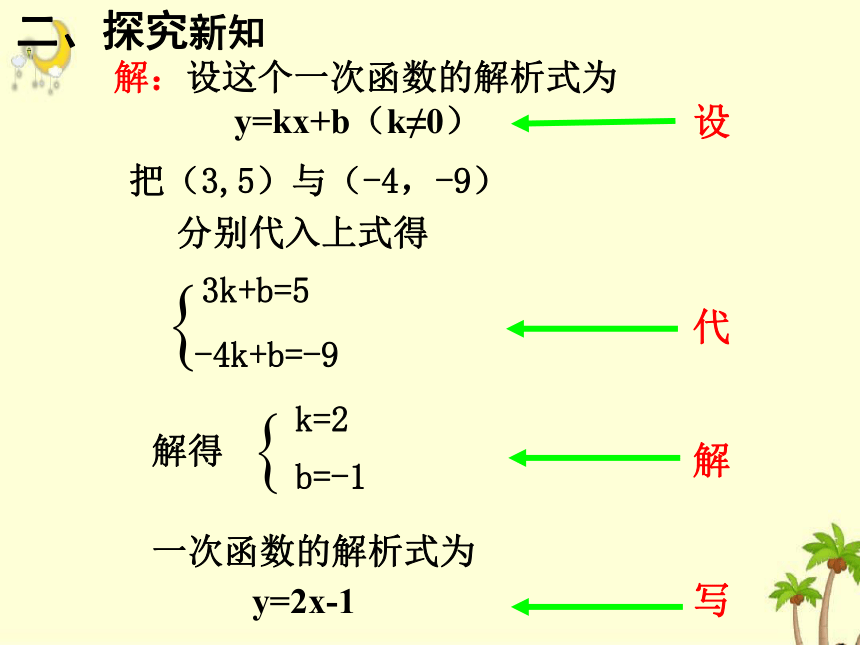
解:设这个一次函数的解析式为
y=kx+b(k≠0)
把(3,5)与(-4,-9)
3k+b=5
分别代入上式得
-4k+b=-9
解得
k=2
b=-1
一次函数的解析式为
y=2x-1
设
代
解
写
二、探究新知
思考:确定一次函数表达式的步骤是什么?
1.设:设函数式为y=kx+b(k≠0)
2.代:将点的坐标代入y=kx+b中,列出关于 k、b的方程组
3.解:解方程组,求出k、b的值
4.写:把求出的k、b值代回到表达式中,得 函数式
设,代,解,写
归纳总结:
先设待求的函数关系式(其中含有待定的系数)再根据条件列出方程或方程组,求出待定系数,从而得到所求结果的方法,叫做待定系数法.
所以 所求函数的表达式为__________.
把_______ , _______ 代入表达式得
__________
__________
设所求函数的表达式为_______________,
例2 一次函数的图象经过点(0,2)和点(4,6),求出一次函数的表达式.
解:
y=kx+b(k≠0)
(0,2)
(4,6)
0×k+b=2
4k+b=6
2
1
y =x+2
解得,
k=_____
b=_____
三、巩固练习
做一做 1. 已知一次函数y=kx+b的图象经过点
(-1,1)和点(1,-5) , 求当x=5时,函数y的值.
根据题意,得
解:
-k+b=1
k+b=-5
解得,
k=-3
b=-2
∴ 函数的解析式为 y= -3x -2
当x=5时,y=-3×5-2=-17
∴ 当x=5时,函数y的值是是-17.
2.一次函数的图象如图所示,求这个一次函数的解析式。
y
x
o
-3
2
解:设一次函数解析式为y=kx+b(k ≠ 0)
根据题意得:
-3k+b=0
k×0+b=2
解得:
k=
2
3
b=2
∴y= x+2
y
x
o
-3
2
2
3
四、整合提升
一次函数 的图像与 的图像交于点P(2,m),求k、m的值。
解:
又 点P(2,m)在直线 上
点P(2,m)在直线 上
通过本节课的学习,你有哪些收获
五、学后反思:
2.用待定系数法解题一般分为几步?
一设、二代、三解、四写
1.设一次函数的一般形式y=kx+b(k≠0)
2.将点的坐标代入y=kx+b中,列出关于 k、b的方程组
3.解这个方程组,求出k ,b
4.将已经求出的 k,b的值代入解析式
六、课堂小结
1.待定系数法:
先设待求的函数关系式(其中含有未知的系数)再根据条件列出方程或方程组,求出未知系数,从而得到所求结果的方法,叫做待定系数法.
作业
课本第52页 习题 6,8,9
谢谢
求一次函数的表达式
教材版本: 2013年华东师范大学出版社 学段学科: 初中数学
年级学期: 八年级 下册
问题1 前面,我们学习了一次函数及其图象和性
质,你还记得一次函数的一般解析式吗?
思考:
反过来已知一个一次函数的图象经过两个具体的点,
你能求出它的解析式吗?
两点法——两点确定一条直线
一、复习引入
问题2 你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
(k≠0)
设所求函数的表达式为_______________,
解:
y=kx+b(k≠0)
根据题意,得
10k+b=10
50k+b=18
解得,
k=0.2
b=8
∴所求函数表达式为 y= 0.2x +8(-20≤x≤100))
问题:温度计中水银(或酒精)柱的高度y(厘米)是温度x(℃)的一次函数。某种型号的实验用水银温度计能测量-20℃至100℃的温度,已知10℃时水银柱高10厘米,50℃时水银柱高18厘米。求这个函数的表达式。
例1:已知一次函数的图象经过点(3,5)与
(-4,-9).求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b(k≠0).
3k+b=5
∴这个一次函数的解析式为
二、探究新知
函数的图象过点
(3,5)与(-4,-9),因此这两点的坐标适合一次函数y=kx+b.
解方程组得
把点(3,5)与(-4,-9)分别代入,得:
k=2
y=2x-1
b=-1
-4k+b=-9
解:设这个一次函数的解析式为
y=kx+b(k≠0)
把(3,5)与(-4,-9)
3k+b=5
分别代入上式得
-4k+b=-9
解得
k=2
b=-1
一次函数的解析式为
y=2x-1
设
代
解
写
二、探究新知
思考:确定一次函数表达式的步骤是什么?
1.设:设函数式为y=kx+b(k≠0)
2.代:将点的坐标代入y=kx+b中,列出关于 k、b的方程组
3.解:解方程组,求出k、b的值
4.写:把求出的k、b值代回到表达式中,得 函数式
设,代,解,写
归纳总结:
先设待求的函数关系式(其中含有待定的系数)再根据条件列出方程或方程组,求出待定系数,从而得到所求结果的方法,叫做待定系数法.
所以 所求函数的表达式为__________.
把_______ , _______ 代入表达式得
__________
__________
设所求函数的表达式为_______________,
例2 一次函数的图象经过点(0,2)和点(4,6),求出一次函数的表达式.
解:
y=kx+b(k≠0)
(0,2)
(4,6)
0×k+b=2
4k+b=6
2
1
y =x+2
解得,
k=_____
b=_____
三、巩固练习
做一做 1. 已知一次函数y=kx+b的图象经过点
(-1,1)和点(1,-5) , 求当x=5时,函数y的值.
根据题意,得
解:
-k+b=1
k+b=-5
解得,
k=-3
b=-2
∴ 函数的解析式为 y= -3x -2
当x=5时,y=-3×5-2=-17
∴ 当x=5时,函数y的值是是-17.
2.一次函数的图象如图所示,求这个一次函数的解析式。
y
x
o
-3
2
解:设一次函数解析式为y=kx+b(k ≠ 0)
根据题意得:
-3k+b=0
k×0+b=2
解得:
k=
2
3
b=2
∴y= x+2
y
x
o
-3
2
2
3
四、整合提升
一次函数 的图像与 的图像交于点P(2,m),求k、m的值。
解:
又 点P(2,m)在直线 上
点P(2,m)在直线 上
通过本节课的学习,你有哪些收获
五、学后反思:
2.用待定系数法解题一般分为几步?
一设、二代、三解、四写
1.设一次函数的一般形式y=kx+b(k≠0)
2.将点的坐标代入y=kx+b中,列出关于 k、b的方程组
3.解这个方程组,求出k ,b
4.将已经求出的 k,b的值代入解析式
六、课堂小结
1.待定系数法:
先设待求的函数关系式(其中含有未知的系数)再根据条件列出方程或方程组,求出未知系数,从而得到所求结果的方法,叫做待定系数法.
作业
课本第52页 习题 6,8,9
谢谢
