2022-2023学年数学沪教版(上海)六年级第一学期 4.1 圆的周长 教案 (含答案)
文档属性
| 名称 | 2022-2023学年数学沪教版(上海)六年级第一学期 4.1 圆的周长 教案 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 81.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-19 20:20:13 | ||
图片预览


文档简介
4.1圆的周长
教学目标:
1.在“观察——猜想——实验——归纳——验证”的过程中获得圆的周长C与直径d的数量关系,形成圆的周长公式,并会用圆的周长公式进行简单问题的计算.
2.在操作实验中,感悟“化曲为直”的数学思想,发展合作、交流的意识.能从我国古代数学家的事迹中感悟民族精神的震撼.
教学重点:
掌握和灵活运用圆的周长公式进行计算.
教学难点:
理解圆周率的意义,灵活运用圆的周长公式进行计算.
课前准备:
每位学生准备一元和五角的硬币各一枚,一些圆形的物品(例如瓶盖等),一根细线和一把刻度尺,计算器.
教学过程:
教师活动
新课导入 图片欣赏 美丽的圆 大自然和生活中,形形色色的优美图案围绕着我们,人们在享受美的同时也在思考着:这些形体有什么特殊的性质?如何在数学上来研究它们呢? 思考 同时从某点出发以相同速度行驶,谁先回到起点? 圆的各部分名称 半径:圆上任意点到圆心的距离都相等,这个距离就叫做圆的半径。 直径:通过圆心且两个端点在圆上的线段叫做圆的直径。 d=2r 直径是半径的两倍 实验与探究 用什么办法“化曲为直”测量出圆的周长呢? 一、绕线法 二、滚动法 圆的周长÷直径=圆周率 (C=πd) 圆的周长÷2半径=圆周率
(C=2πr) 无特殊说明:π取3.14,将计算结果精确到0.01 谐音故事:古时候,有位教学先生,他特别喜欢喝酒。一天,他向他的弟子讲解到圆的周长的时候,突然想到了喝酒,就对自己的弟子说,你们把圆周率给背熟,会被的就上后山顶的那座亭子里找我。后来,一弟子熟背后,跑上山,竟然看到教学先生偷偷在后山顶的亭里喝酒,他突然灵感一现: “3.1415926535897932384626” 山巅一寺一壶酒(3.14159) 尔乐苦煞吾(26535) 把酒吃(897) 酒杀尔(932) 杀不死(384) 乐尔乐(626) 0.5π=1.57 π取3.14 2π=6.28 3π=9.42 4π=12.56 5π=15.7 6π=18.84 7π=21.98 8π=25.12 9π=28.26 11π=34.54
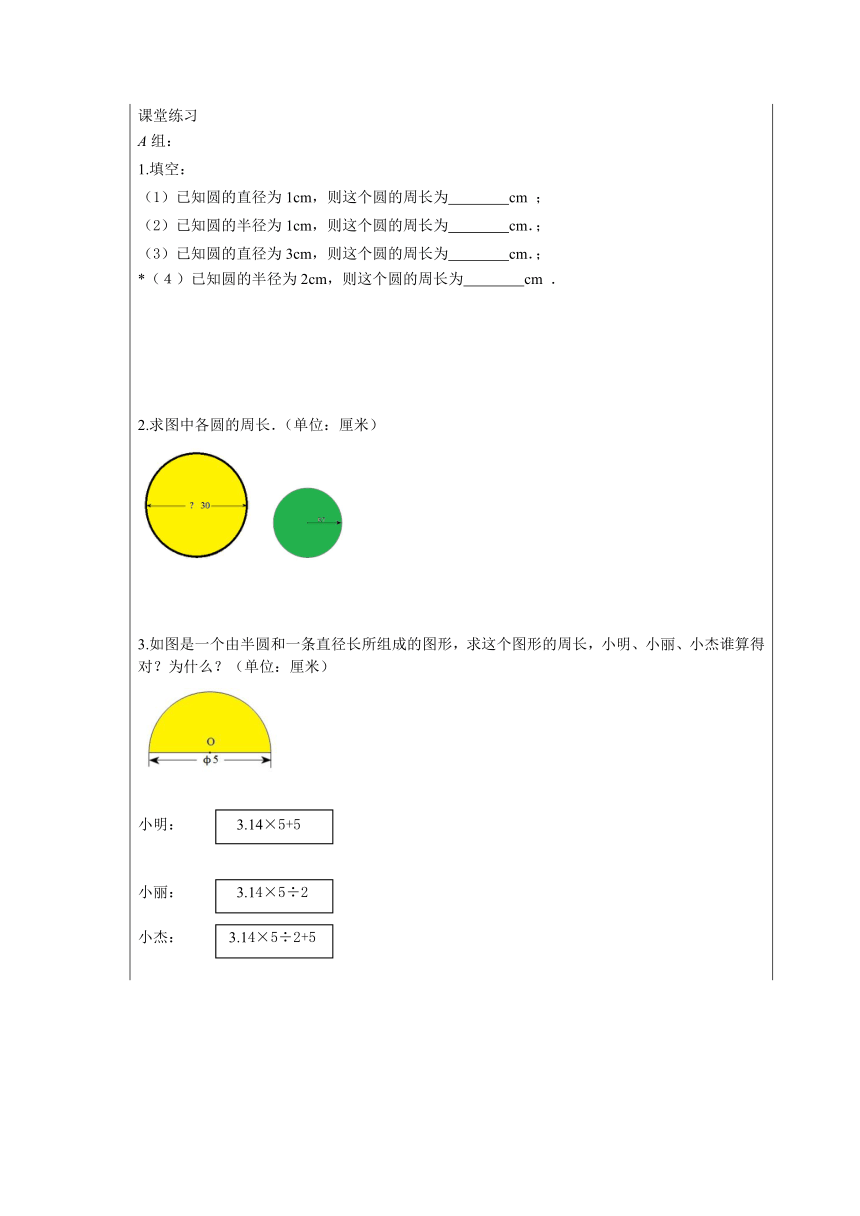
课堂练习 A组: 1.填空: (1)已知圆的直径为1cm,则这个圆的周长为 cm ; (2)已知圆的半径为1cm,则这个圆的周长为 cm.; (3)已知圆的直径为3cm,则这个圆的周长为 cm.; *(4)已知圆的半径为2cm,则这个圆的周长为 cm .
2.求图中各圆的周长.(单位:厘米)
3.如图是一个由半圆和一条直径长所组成的图形,求这个图形的周长,小明、小丽、小杰谁算得对?为什么?(单位:厘米) 小明: 3.14×5+5 小丽: 3.14×5÷2 小杰: 3.14×5÷2+5
B组: 1.判断题: (1)圆的周长是半径的2倍;( ) (2)小圆的圆周率比大圆的圆周率小;( ) *(3)=3.14 ( )
2.有一奶牛场准备用粗铁丝围成一个半径长是120米的圆形牛栏,如果用铁丝围三圈,那么,至少需要买多少米铁丝?(接头处忽略不计.) 3.如图,计算环行跑道的周长.(单位:米)
自主评价,升化新知 1.学生小结:今天有什么收获想和同学一起分享? 2.教师补充小结: (1)应根据已知条件正确选择圆的周长公式:C圆=;C圆= (2)我们通过“观察——猜想——实验——归纳——验证”的过程来探索圆的周长公式,在这过程中,我们可以初步感受到数学研究的一般过程.
课后作业:
试 题 解 答 设计意图
A组 1.小琳家的闹钟的分针长6厘米,在一小时内它的分针的针尖所经过的路程总长为多少厘米?(精确到1厘米)(练习册P49) 分析:分针长6厘米即为圆的半径,针尖经过的路程即为圆,所求总长即为圆的周长. 解:r=6, C=2r=2×3.14×6=37.68 ≈38(厘米). 答:路程总长约为38厘米. 能把生活中的实际问题转化为求圆的周长问题.
2.圆形水池的周长是78.5m,它的直径是多少?半径是多少?(精确到0.1m) 练习册P49 分析:圆形水池的周长78.5m,即是圆的周长,已知周长求直径和半径. 解:C=78.5, 由 C=d, 得 78.5=3.14d, 所以d=78.5÷3.14=25(米), r=24.8÷3.14=12.5(米). 答:它的直径约是25米,半径约是12.5米. 已知圆的周长求半径或直径,代入周长公式,利用解方程方法来解.避免公式变形,来降低难度.
B组: *1.判断题: (1) 圆周率的值是圆周长与直径的比值 ( ); (2)圆周率的值是一个无限不循环的小数 ( ); (3)圆的半径越大,圆周长越大 ( ); (4)圆的周长越大,圆周率越大 ( ); (5)圆周率的值与圆的大小无关 ( ). (1)√(由圆周率意义); (2)√(圆周率意义); (3)√(由圆周长公式知,正确); (4)×;(由圆周率意义,圆周率与圆周长的大小无关); (5)√(圆周率意义). 理解并熟练掌握圆周率的意义,以及圆周长公式,能正确应用其进行辨析正误.
2.小明在一条路上滚铁环,铁环的直径是30厘米,滚动过了47.1米,问铁环滚动了几圈?(精确到1圈)(练习册P49) 分析:铁环直径是30厘米,可求出铁环的周长,滚动了47.1米是几圈,就是求47.1米有几个铁环的周长. 解:d=30 C=d=3.14×30=942(厘米) 47.1米=4710厘米 4710÷C=4710÷94.2=50(圈) 答:铁环滚动了50圈. 圆周长公式的实际应用,把实际问题转化为圆的周长问题.
3.以一根长20cm的细钢丝为材料,制作三个同样大小的圆形钢丝环(不计接口处的损耗),结果还余下1.16厘米长的钢丝,那么,制作的圆形钢丝环的直径是多少厘米?(练习册P49) 分析:所求问题实际是三个圆的周长是(20-1.16)cm,求出一个圆的周长,再求直径. 解: C=(20-1.16)÷3 =18.84÷3=6.28(厘米), 因为C=d, 所以6.28=3.14d, d=6.28÷3.14=2(厘米). 答:制作的圆形钢丝环的直径是2厘米. 应用圆周长公式解决实际问题.
C组: *1.已知自行车轮子的直径为0.8米,每分钟能滚动25圈,要通过一座长502.4米的大桥,需要多少分钟? 分析:先求出直径为8米的轮子的周长,即滚动1圈的路程,再求出滚动25圈是多少米,即一分钟所滚动的路程,再算出502.4米是这个路程的多少倍,就是几分钟. 解:d=0.8, C=d=3.14×0.8=2.512(米), 25C=25×2.512=62.8(米), 502.4÷62.8=8(分钟). 答:需要8分钟. 将实际问题正确转化为圆周长公式加以解决.
2.如图,甲乙两只蚂蚁同时从A点 出发,甲沿着外侧的大圆爬行,乙在里面两个小圆沿“8”字型爬行,如果两只蚂蚁爬行的速度相同,问:是甲先回到A点,还是乙先回到A点?或者他们同时回到A点?为什么?练习册P50 分析:甲沿着外侧的大圆爬行,即甲爬行了大圆的圆周长;乙在里面两个小圆沿“8”字型爬行,“8”字型即为两个小圆的周长的和. 解:甲、乙两只蚂蚁同时回到A点. 理由:设中圆的半径是d,小圆的半径是d,则大圆半径是d+ d. 甲蚂蚁爬行的路程是: (d+ d)= d+ d , 乙蚂蚁爬行的路程是: d+ d . 即甲、乙两只蚂蚁所爬行的路程相等,所以同时回到A点. 本题学生可能不易理解,会认为不能同时到达,或说不清理由. 老师可加以提示,引导学生用设未知数,分别求出它们所爬行的路程,说明相等.
教学目标:
1.在“观察——猜想——实验——归纳——验证”的过程中获得圆的周长C与直径d的数量关系,形成圆的周长公式,并会用圆的周长公式进行简单问题的计算.
2.在操作实验中,感悟“化曲为直”的数学思想,发展合作、交流的意识.能从我国古代数学家的事迹中感悟民族精神的震撼.
教学重点:
掌握和灵活运用圆的周长公式进行计算.
教学难点:
理解圆周率的意义,灵活运用圆的周长公式进行计算.
课前准备:
每位学生准备一元和五角的硬币各一枚,一些圆形的物品(例如瓶盖等),一根细线和一把刻度尺,计算器.
教学过程:
教师活动
新课导入 图片欣赏 美丽的圆 大自然和生活中,形形色色的优美图案围绕着我们,人们在享受美的同时也在思考着:这些形体有什么特殊的性质?如何在数学上来研究它们呢? 思考 同时从某点出发以相同速度行驶,谁先回到起点? 圆的各部分名称 半径:圆上任意点到圆心的距离都相等,这个距离就叫做圆的半径。 直径:通过圆心且两个端点在圆上的线段叫做圆的直径。 d=2r 直径是半径的两倍 实验与探究 用什么办法“化曲为直”测量出圆的周长呢? 一、绕线法 二、滚动法 圆的周长÷直径=圆周率 (C=πd) 圆的周长÷2半径=圆周率
(C=2πr) 无特殊说明:π取3.14,将计算结果精确到0.01 谐音故事:古时候,有位教学先生,他特别喜欢喝酒。一天,他向他的弟子讲解到圆的周长的时候,突然想到了喝酒,就对自己的弟子说,你们把圆周率给背熟,会被的就上后山顶的那座亭子里找我。后来,一弟子熟背后,跑上山,竟然看到教学先生偷偷在后山顶的亭里喝酒,他突然灵感一现: “3.1415926535897932384626” 山巅一寺一壶酒(3.14159) 尔乐苦煞吾(26535) 把酒吃(897) 酒杀尔(932) 杀不死(384) 乐尔乐(626) 0.5π=1.57 π取3.14 2π=6.28 3π=9.42 4π=12.56 5π=15.7 6π=18.84 7π=21.98 8π=25.12 9π=28.26 11π=34.54
课堂练习 A组: 1.填空: (1)已知圆的直径为1cm,则这个圆的周长为 cm ; (2)已知圆的半径为1cm,则这个圆的周长为 cm.; (3)已知圆的直径为3cm,则这个圆的周长为 cm.; *(4)已知圆的半径为2cm,则这个圆的周长为 cm .
2.求图中各圆的周长.(单位:厘米)
3.如图是一个由半圆和一条直径长所组成的图形,求这个图形的周长,小明、小丽、小杰谁算得对?为什么?(单位:厘米) 小明: 3.14×5+5 小丽: 3.14×5÷2 小杰: 3.14×5÷2+5
B组: 1.判断题: (1)圆的周长是半径的2倍;( ) (2)小圆的圆周率比大圆的圆周率小;( ) *(3)=3.14 ( )
2.有一奶牛场准备用粗铁丝围成一个半径长是120米的圆形牛栏,如果用铁丝围三圈,那么,至少需要买多少米铁丝?(接头处忽略不计.) 3.如图,计算环行跑道的周长.(单位:米)
自主评价,升化新知 1.学生小结:今天有什么收获想和同学一起分享? 2.教师补充小结: (1)应根据已知条件正确选择圆的周长公式:C圆=;C圆= (2)我们通过“观察——猜想——实验——归纳——验证”的过程来探索圆的周长公式,在这过程中,我们可以初步感受到数学研究的一般过程.
课后作业:
试 题 解 答 设计意图
A组 1.小琳家的闹钟的分针长6厘米,在一小时内它的分针的针尖所经过的路程总长为多少厘米?(精确到1厘米)(练习册P49) 分析:分针长6厘米即为圆的半径,针尖经过的路程即为圆,所求总长即为圆的周长. 解:r=6, C=2r=2×3.14×6=37.68 ≈38(厘米). 答:路程总长约为38厘米. 能把生活中的实际问题转化为求圆的周长问题.
2.圆形水池的周长是78.5m,它的直径是多少?半径是多少?(精确到0.1m) 练习册P49 分析:圆形水池的周长78.5m,即是圆的周长,已知周长求直径和半径. 解:C=78.5, 由 C=d, 得 78.5=3.14d, 所以d=78.5÷3.14=25(米), r=24.8÷3.14=12.5(米). 答:它的直径约是25米,半径约是12.5米. 已知圆的周长求半径或直径,代入周长公式,利用解方程方法来解.避免公式变形,来降低难度.
B组: *1.判断题: (1) 圆周率的值是圆周长与直径的比值 ( ); (2)圆周率的值是一个无限不循环的小数 ( ); (3)圆的半径越大,圆周长越大 ( ); (4)圆的周长越大,圆周率越大 ( ); (5)圆周率的值与圆的大小无关 ( ). (1)√(由圆周率意义); (2)√(圆周率意义); (3)√(由圆周长公式知,正确); (4)×;(由圆周率意义,圆周率与圆周长的大小无关); (5)√(圆周率意义). 理解并熟练掌握圆周率的意义,以及圆周长公式,能正确应用其进行辨析正误.
2.小明在一条路上滚铁环,铁环的直径是30厘米,滚动过了47.1米,问铁环滚动了几圈?(精确到1圈)(练习册P49) 分析:铁环直径是30厘米,可求出铁环的周长,滚动了47.1米是几圈,就是求47.1米有几个铁环的周长. 解:d=30 C=d=3.14×30=942(厘米) 47.1米=4710厘米 4710÷C=4710÷94.2=50(圈) 答:铁环滚动了50圈. 圆周长公式的实际应用,把实际问题转化为圆的周长问题.
3.以一根长20cm的细钢丝为材料,制作三个同样大小的圆形钢丝环(不计接口处的损耗),结果还余下1.16厘米长的钢丝,那么,制作的圆形钢丝环的直径是多少厘米?(练习册P49) 分析:所求问题实际是三个圆的周长是(20-1.16)cm,求出一个圆的周长,再求直径. 解: C=(20-1.16)÷3 =18.84÷3=6.28(厘米), 因为C=d, 所以6.28=3.14d, d=6.28÷3.14=2(厘米). 答:制作的圆形钢丝环的直径是2厘米. 应用圆周长公式解决实际问题.
C组: *1.已知自行车轮子的直径为0.8米,每分钟能滚动25圈,要通过一座长502.4米的大桥,需要多少分钟? 分析:先求出直径为8米的轮子的周长,即滚动1圈的路程,再求出滚动25圈是多少米,即一分钟所滚动的路程,再算出502.4米是这个路程的多少倍,就是几分钟. 解:d=0.8, C=d=3.14×0.8=2.512(米), 25C=25×2.512=62.8(米), 502.4÷62.8=8(分钟). 答:需要8分钟. 将实际问题正确转化为圆周长公式加以解决.
2.如图,甲乙两只蚂蚁同时从A点 出发,甲沿着外侧的大圆爬行,乙在里面两个小圆沿“8”字型爬行,如果两只蚂蚁爬行的速度相同,问:是甲先回到A点,还是乙先回到A点?或者他们同时回到A点?为什么?练习册P50 分析:甲沿着外侧的大圆爬行,即甲爬行了大圆的圆周长;乙在里面两个小圆沿“8”字型爬行,“8”字型即为两个小圆的周长的和. 解:甲、乙两只蚂蚁同时回到A点. 理由:设中圆的半径是d,小圆的半径是d,则大圆半径是d+ d. 甲蚂蚁爬行的路程是: (d+ d)= d+ d , 乙蚂蚁爬行的路程是: d+ d . 即甲、乙两只蚂蚁所爬行的路程相等,所以同时回到A点. 本题学生可能不易理解,会认为不能同时到达,或说不清理由. 老师可加以提示,引导学生用设未知数,分别求出它们所爬行的路程,说明相等.
