2023—2024学年人教版数学八年级上册 11.1.2 三角形的高、中线与角平分线 同步精练 (无答案)
文档属性
| 名称 | 2023—2024学年人教版数学八年级上册 11.1.2 三角形的高、中线与角平分线 同步精练 (无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 248.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-19 20:46:11 | ||
图片预览

文档简介
11.1.2 三角形的高、中线与角平分线 同步精练
一、单选题
1.在中,画出边上的高,画法正确的是( )
A.B.C.D.
2.如图,,,分别是的高、角平分线、中线、则下列各式中错误的是( )
A.
B.
C.
D.
3.如图所示,在中,,以AD为高的三角形有( )个.
A.3 B.4 C.5 D.6
4.AD是的中线,已知的周长为25cm,AB比AC长6cm,则的周长为( )
A.19cm B.22cm C.25cm D.31cm
5.如图,在△ABC中,∠C=90°,D,E是AC上两点,且AE=DE,BD平分∠EBC,那么下列说法中不正确的是( )
A.BE是△ABD的中线 B.BD是△BCE的角平分线
C.∠1=∠2=∠3 D.BC是△ABE的高
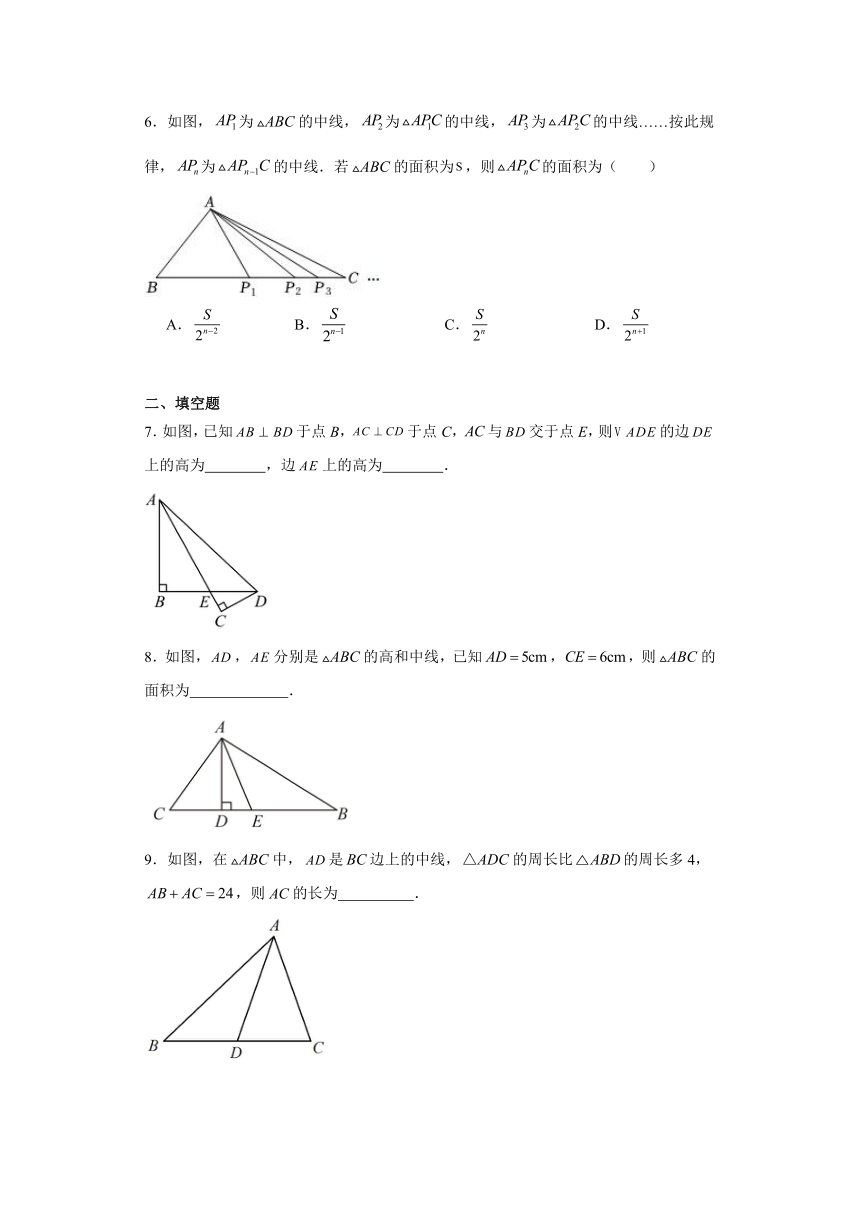
6.如图,为的中线,为的中线,为的中线……按此规律,为的中线.若的面积为,则的面积为( )
A. B. C. D.
二、填空题
7.如图,已知于点B,于点C,与交于点E,则的边上的高为 ,边上的高为 .
8.如图,,分别是的高和中线,已知,,则的面积为 .
9.如图,在中,是边上的中线,的周长比的周长多4,,则AC的长为 .
10.如图,已知中,,现将进行折叠,使顶点、均与顶点重合,则的度数为 .
11.在△ABC中,,AC上的中线BD把三角形的周长分为21和12两部分,则三角形各边长为 .
12.如图,中,,P为直线上一动点,连,则线段的最小值是 .
三、解答题
13.如图,已知,
求作:(1)边上的高;(2)边上的高.
14.如图,△ABC中,∠A=46°,CE是∠ACB的平分线,B、C、D在同一直线上,FD∥EC,∠D=42°,求证:∠B=50°.
15.如图所示,已知△ABC的周长为21 cm,AB=6 cm,BC边上中线AD=5 cm,△ABD的周长为15 cm,求AC的长.
16.如图,在中(),,边上的中线把的周长分成60和40两部分,求和的长.
17.如图,在三角形ABC中,∠C=90°,把三角形ABC沿直线DE折叠,使三角形ADE与三角形BDE重合
(1)若∠A=30°,求∠CBD的度数
(2)若三角形BCD的周长为12,AE=5,求三角形ABC的周长
18.四边形是大家最熟悉的图形之一,我们已经发现了它的许多性质.只要善于观察、乐于探索,我们还会发现更多的结论.
(1)四边形一条对角线上任意一点与另外两个顶点的连线,将四边形分成四个三角形(如图①),其中相对的两对三角形的面积之积相等.你能证明这个结论吗?试试看.
已知:在四边形ABCD中, O是对角线BD上任意一点.(如图①)求证: ;
(2)在三角形中(如图②),你能否归纳出类似的结论?若能,写出你猜想的结论,并证明:若不能,说明理由.
一、单选题
1.在中,画出边上的高,画法正确的是( )
A.B.C.D.
2.如图,,,分别是的高、角平分线、中线、则下列各式中错误的是( )
A.
B.
C.
D.
3.如图所示,在中,,以AD为高的三角形有( )个.
A.3 B.4 C.5 D.6
4.AD是的中线,已知的周长为25cm,AB比AC长6cm,则的周长为( )
A.19cm B.22cm C.25cm D.31cm
5.如图,在△ABC中,∠C=90°,D,E是AC上两点,且AE=DE,BD平分∠EBC,那么下列说法中不正确的是( )
A.BE是△ABD的中线 B.BD是△BCE的角平分线
C.∠1=∠2=∠3 D.BC是△ABE的高
6.如图,为的中线,为的中线,为的中线……按此规律,为的中线.若的面积为,则的面积为( )
A. B. C. D.
二、填空题
7.如图,已知于点B,于点C,与交于点E,则的边上的高为 ,边上的高为 .
8.如图,,分别是的高和中线,已知,,则的面积为 .
9.如图,在中,是边上的中线,的周长比的周长多4,,则AC的长为 .
10.如图,已知中,,现将进行折叠,使顶点、均与顶点重合,则的度数为 .
11.在△ABC中,,AC上的中线BD把三角形的周长分为21和12两部分,则三角形各边长为 .
12.如图,中,,P为直线上一动点,连,则线段的最小值是 .
三、解答题
13.如图,已知,
求作:(1)边上的高;(2)边上的高.
14.如图,△ABC中,∠A=46°,CE是∠ACB的平分线,B、C、D在同一直线上,FD∥EC,∠D=42°,求证:∠B=50°.
15.如图所示,已知△ABC的周长为21 cm,AB=6 cm,BC边上中线AD=5 cm,△ABD的周长为15 cm,求AC的长.
16.如图,在中(),,边上的中线把的周长分成60和40两部分,求和的长.
17.如图,在三角形ABC中,∠C=90°,把三角形ABC沿直线DE折叠,使三角形ADE与三角形BDE重合
(1)若∠A=30°,求∠CBD的度数
(2)若三角形BCD的周长为12,AE=5,求三角形ABC的周长
18.四边形是大家最熟悉的图形之一,我们已经发现了它的许多性质.只要善于观察、乐于探索,我们还会发现更多的结论.
(1)四边形一条对角线上任意一点与另外两个顶点的连线,将四边形分成四个三角形(如图①),其中相对的两对三角形的面积之积相等.你能证明这个结论吗?试试看.
已知:在四边形ABCD中, O是对角线BD上任意一点.(如图①)求证: ;
(2)在三角形中(如图②),你能否归纳出类似的结论?若能,写出你猜想的结论,并证明:若不能,说明理由.
