北师大版九年级数学上册1.3正方形的性质与判定 同步练习题(含解析)
文档属性
| 名称 | 北师大版九年级数学上册1.3正方形的性质与判定 同步练习题(含解析) | 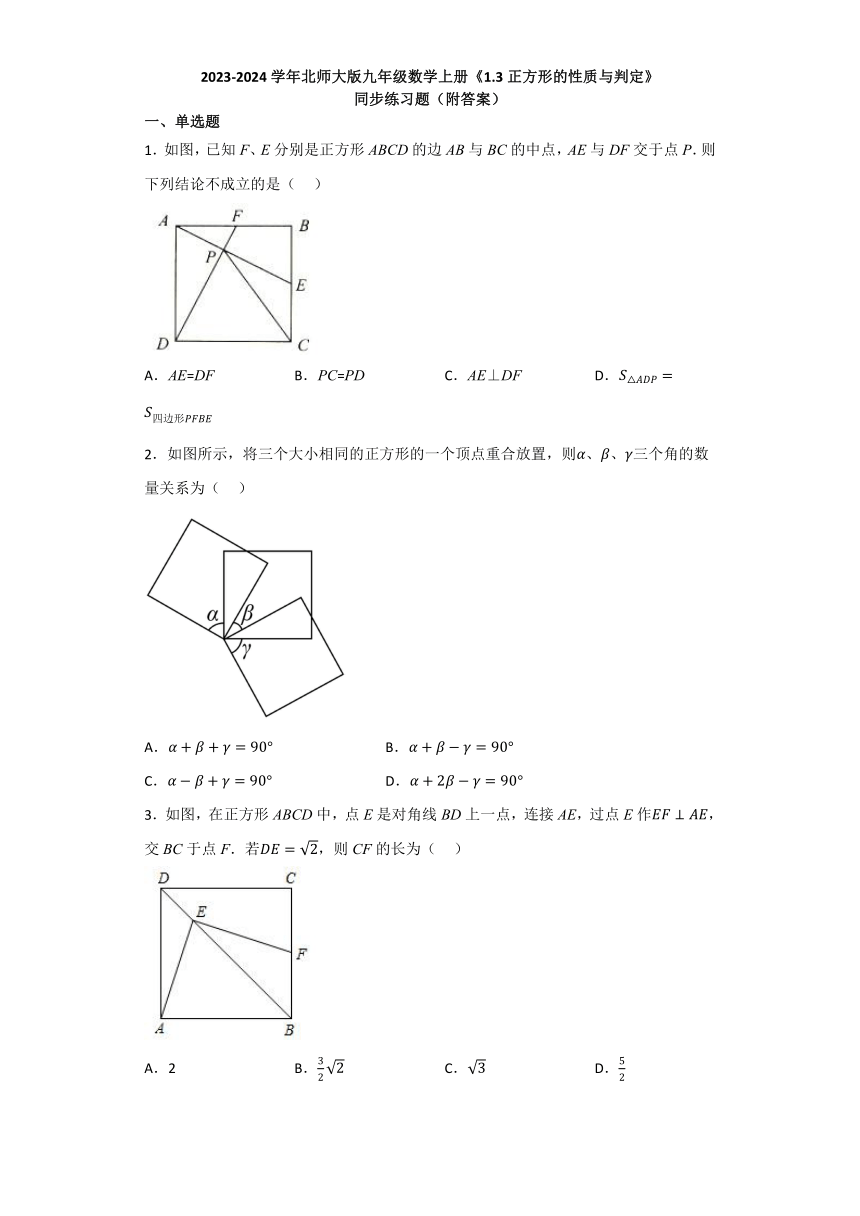 | |
| 格式 | docx | ||
| 文件大小 | 806.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 09:04:21 | ||
图片预览





文档简介
2023-2024学年北师大版九年级数学上册《1.3正方形的性质与判定》
同步练习题(附答案)
一、单选题
1.如图,已知F、E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P.则下列结论不成立的是( )
A.AE=DF B.PC=PD C.AE⊥DF D.
2.如图所示,将三个大小相同的正方形的一个顶点重合放置,则、、三个角的数量关系为( )
B.
C. D.
3.如图,在正方形ABCD中,点E是对角线BD上一点,连接AE,过点E作,交BC于点F.若,则CF的长为( )
A.2 B. C. D.
4.如图,在正方形中,,E,F分别为边的中点,连接,点G,H分别为的中点,连接,则的长为( )
A. B.1 C. D.2
5.如图,正方形ABCD和正方形CEFG中,点D在CG上,已知BC=1,CE=7,点H是AF的中点,则CH的长是( )
A.5 B.3.5 C.4 D.
6.如图,正方形ABCD的面积为12,△ABE是等边三角形且点E在正方形内,点P在对角线AC上,连结PD,PE,则PD+PE的最小值为( )
A.12 B.6 C.2 D.4
7.如图,在平面直角坐标系中,将边长为a的正方形OABC绕点O顺时针旋转后得到正方形,依此方式连续旋转2023次得到正方形,那么点的坐标是( )
A.(a,a) B. C. D.
二、填空题
8.如图,边长为4的正方形ABCD中对角线AC、BD相交于点O,OE⊥CD,则OE=___________ .
9.如图,正方形ABCD的边长为3,E在BC上,且BE=2,P在BD上,则△PEC周长的最小值为_______.
10.如图,在四边形ABCD中,AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=90°,边AD绕点A顺时针旋转角度m(0°<m<360°),得到线段AP,连接PB,PC.当△BPC是等腰三角形时,m的值为_______.
11.如图,正方形ABCD中,点E,F分别在AD,CD上.且DE=CF,AF与BE相交于点G.若AB=4,DE=1,则GF的长 ____
12.如图,正方形和正方形的边长分别是4和6,且点,,在同一直线上,是线段的中点,连接,则的长为_________.
13.如图所示,以Rt△ABC的两直角边AC,BC分别作正方形ACED和正方形BCFG,连接EF;过点C作CH⊥AB于点H并反方向延长交EF于点I,若正方形ACED和正方形BCFG面积分别为16和9,则HI长为______.
14.如图,在正方形ABCD中,F在AB上,E在BC的延长线上,AF=CE,连接DF、DE、EF,EF交对角线BD于点N,M为EF的中点,连接MC,下列结论:①△DEF为等腰直角三角形;②∠FDB=∠FEC;③直线MC是BD的垂直平分线;④若BF=2,则MC=;其中正确结论的有_______.
三、解答题
15.问题情境:四边形中,点O是对角线的中点,点E是直线上的一个动点(点E与点C、O、A都不重合)过点A,C分别作直线的垂线,垂足分别为F、G,连接.
(1)初步探究:已知四边形是正方形,且点E在线段上,求证;
(2)探究图中与的数量关系,并说明理由.
16.如图,在四边形中,且,对角线和相交于点O,且,过点B作,交于点E,连结.
(1)求证:;
(2)试探究四边形的形状,并说明理由;
(3)若,,,求四边形的面积.
17.已知正方形如图所示,连接其对角线,的平分线交于点,过点作于点,交于点,过点作,交延长线于点P.
(1)求证:;
(2)若正方形的边长为4,求的面积;
(3)求证:.
18.(1)建立模型:如图1,在正方形中,E,F分别是上的点,且,探究图中线段之间的数量关系.小王同学探究此问题的方法是将绕A点逆时针旋转使得B与D重合,连接,由此得到______,再证明______,可得出线段之间的数量关系为______.
(2)拓展延伸:如图2,在等腰直角三角形中,,点G,H在边上,且,写出图中线段之间的数量关系并证明.
19.如图,四边形是正方形,点E是平面内异于点A的任意一点,以线段为边作正方形,连接.
(1)如图1,求证:;
(2)如图2,若点E在线段上,,,求的长.
20.如图1,在正方形中,E是边上的一动点(不与B重合),,,交于点G,连接.
(1)若,E为的中点,则 ;
(2)探究线段与的数量关系,并给出证明;
(3)如图2,连接,比较和的大小关系,并说明理由.
参考答案
1.解:∵四边形是正方形,
∴,
∵F、E分别是正方形的边与的中点,
∴,
∴,
∴,选项A正确,不符合题意;
∴,
又∵,
∴,
∴,,选项C正确,不符合题意:
由得,
∴,即,选项D正确:
只有选项B无法证明其成立,
故选B.
2.解:如图:
三个大小相同的正方形,
∵,,
又∵,
∴,即,
故选:C.
3.解:如图,过点E作EH⊥BC交AD于G,
∵四边形ABCD是正方形,
∴ADBC,∠ЕВН=∠ADB=45°,
∴四边形AGHB和四边形DGHC是矩形,△DGE是等腰直角三角形,
∴AG=BH=ЕН,DG=EG=1,
∴CH = DG= 1,
∵AG⊥GH,AE⊥EF,
∴∠AGE=∠AEF=∠FHE= 90°,
∴∠GAE+∠AEG=∠FEH+∠AEG= 90°,
∴∠GAE= ∠FEH,
∴△AGE≌△EHF(AAS),
∴GE= FH= 1,
∴CF= CH + FH= 2,
故选:A.
4.解:连接AG,延长AG交CD于M,连接FM,
∵四边形ABCD是正方形,
∴AB=CD=BC=AD=4,ABCD,∠C=90°,
∴∠AEG=∠GDM,∠EAG=∠DMG,
∵G为DE的中点,
∴GE=GD,
∴△AEG≌△MDG(AAS),
∴AG=MG,AE=DM=AB=CD,
∴CM=CD=2,
∵点H为AF的中点,
∴GH=FM,
∵F为BC的中点,
∴CF=BC=2,
∴FM=,
∴GH=FM=,
故选:C.
5.解:延长AD交EF于M,连接AC、CF,
∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=7,
∴AB=BC=1,CE=EF=7,∠E=90°,
则AM=BC+CE=1+7=8,FM=EF-AB=7-1=6,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH=AF,
在Rt△AMF中,由勾股定理得:,
∴CH=5,
故选:A.
6.解:连接PB,
∵正方形ABCD的面积为12,
∴AB=2,点B、D关于对角线AC对称,
∵△ABE是等边三角形,
∴AB=BE=2,
∵点B、D关于对角线AC对称,
∴PD=PB,
∴PD+PE的最小值即为BE的长,
即PD+PE的最小值为.
故选:C.
7.解:如图,过点作轴于点D,
∵四边形OABC是正方形,且OA=a,
∴A(0,a),
,
∵将正方形OABC绕点O顺时针旋转45°后得到正方形,
∴,
∴,
∴,
∴,
∴,
∵正方形绕点O顺时针旋转后得到正方形
∴,
∴,
同理,, ,,,,
……,
由此发现正方形旋转8次为一个循环,
∵2023÷8=252…7,
∴点A2023的坐标与相同,为.
故选:D
8.解:因为四边形ABCD是正方形,
所以OD=OC=OB=OA,
因为OE⊥CD,
根据等腰三角形三线合一,得DE=EC,
所以OE是△DBC的中位线,
所以OE= ,
故答案为:2.
9.解:如图,连接,,
点关于的对称点为点,
,
根据两点之间线段最短可得就是的最小值,
正方形的边长为3,,
,
的最小值是,
则△PEC周长的最小值为:
故答案为:.
10.解:如图1,当m=30°时,
BP=BC,△BPC是等腰三角形;
如图2,当m=60°时,
PB=PC,△BPC是等腰三角形;
如图3,当m=150°时,
PB=BC,△BPC是等腰三角形;
如图4,当m=300°时,
PB=PC,△BPC是等腰三角形;
综上所述,m的值为30°或60°或150°或300°,
故答案为:30°或60°或150°或300°.
11.解:∵四边形形ABCD是正方形,
∴AB=AD=DC,∠BAD=∠D=90°,
又∵DE=CF,
∴AE=DF,
∴在△BAE和△ADF中,
,
∴△BAE≌△ADF(SAS).
∴∠ABE=∠DAF,BE=AF,
∵∠DAF+∠BAG=90°,
∴∠ABE+∠BAG=90°,
∴∠AGB=90°,
∴BE⊥AF.
∵AB=AD=4,DE=1,
∴AE=AD-DE=3,
∴在Rt△ABE中,有,
∴AF=BE=5,
∵BE⊥AF,∠BAD=90°,
∴,
∴,
∴,
故答案为:.
12.解:延长AD至H,延长FM与AH交于H点,
由题意可得ADEF,
∴,
∵是线段的中点,
∴,
∴在△AMH和△EMF中,
∴△AMH≌△EMF,
即FM=MH,AH=EF,
∴DH=AH-AD=EF-AD=2,
∵DF=CF-CD=6-4=2,
在直角△DFH中,FH为斜边,
∴FH=,
∵FM=MH,
∴FM=.
故答案为:.
13.解:∵正方形ACED和正方形BCFG面积分别为16和9,
∴,
中,,
依题意,,
∴,
∴,
∵,
∴,
又,
∴,
∴,
同理可得,
∴,
,
,
∴.
故答案为:4.9.
14.解:四边形是正方形,
,
在和中,,
,
,
,
为等腰直角三角形,结论①正确;
,
又,
,
即,结论②正确;
如图,连接,
为和斜边上的中点,
,
又,
直线是的垂直平分线,结论③正确;
如图,取的中点,连接,
,
,
直线是的垂直平分线,,
(等腰三角形的三线合一),
是等腰直角三角形,且,
,结论④正确;
综上,正确结论的有①②③④,
故答案为:①②③④.
15.(1)证明:∵四边形是正方形,
∴,
∵,
∴,
∴,
在和中,,
∴,
∴;
(2)解:,理由如下:
如图,延长交于H,
∵,
∴,
∴,
∵,
在和中,
,
∴,
∴,
在中,.
∴.
16.(1)证明:∵,
∴,
在和中,
∵,
∴;
(2)解:四边形是矩形,理由如下:
∵,
∴,
∵,
∴四边形是平行四边形,
∵,
∴四边形是矩形;
(3)解:∵且,
∴,即,
∴四边形是正方形,
∴,
设,则,
在中,由勾股定理得,即,
解得:,(舍去),
∴,
∴,
∴,
∴四边形的面积为18.
17.(1)解:证明:四边形是正方形,
,,
,
,
,
,,
,
;
(2)平分,
,
,
,
,且,
,
,
,
;
(3)在上截取,连接,
,
,
,且,
,
,
,
,
,,
,
,
,
.
18.解:(1)∵四边形是正方形,
∴,
由旋转的性质可知:,
∵,
∴,
∴,
∵,
∴三点共线,
又∵,
∴,
∴,
∵,
∴.
故答案为:;;.
(2),证明如下:
如图所示,将绕点B逆时针旋转得到.
∵,
∴,
由旋转的性质可知:,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
19.(1)证明:∵四边形和四边形都是正方形,
∴,
∴,
在△AGD和△AEB中,
,
∴,
∴;
(2)解:作于H,
∵四边形和四边形都是正方形,
∴,.
由勾股定理得,
∴,
∴,
∴.
20.(1)解:在正方形中,,
∵E为的中点,,
∴,
∴,
故答案为:
(2)解:.
在线段上截取,连接
∵
∴
∴
∵在正方形中
∴
∴
∵
∴
∴
∴
∵,,
∴
∴,
∵在中,
∴
∴;
(3)解:延长至P,使得,连接
∵在正方形中
∴,
∴
∵,,
∴
∴,
∵,
∴
∴
∴
即
∵,,
∴
∴
又∵,
∴.
同步练习题(附答案)
一、单选题
1.如图,已知F、E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P.则下列结论不成立的是( )
A.AE=DF B.PC=PD C.AE⊥DF D.
2.如图所示,将三个大小相同的正方形的一个顶点重合放置,则、、三个角的数量关系为( )
B.
C. D.
3.如图,在正方形ABCD中,点E是对角线BD上一点,连接AE,过点E作,交BC于点F.若,则CF的长为( )
A.2 B. C. D.
4.如图,在正方形中,,E,F分别为边的中点,连接,点G,H分别为的中点,连接,则的长为( )
A. B.1 C. D.2
5.如图,正方形ABCD和正方形CEFG中,点D在CG上,已知BC=1,CE=7,点H是AF的中点,则CH的长是( )
A.5 B.3.5 C.4 D.
6.如图,正方形ABCD的面积为12,△ABE是等边三角形且点E在正方形内,点P在对角线AC上,连结PD,PE,则PD+PE的最小值为( )
A.12 B.6 C.2 D.4
7.如图,在平面直角坐标系中,将边长为a的正方形OABC绕点O顺时针旋转后得到正方形,依此方式连续旋转2023次得到正方形,那么点的坐标是( )
A.(a,a) B. C. D.
二、填空题
8.如图,边长为4的正方形ABCD中对角线AC、BD相交于点O,OE⊥CD,则OE=___________ .
9.如图,正方形ABCD的边长为3,E在BC上,且BE=2,P在BD上,则△PEC周长的最小值为_______.
10.如图,在四边形ABCD中,AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=90°,边AD绕点A顺时针旋转角度m(0°<m<360°),得到线段AP,连接PB,PC.当△BPC是等腰三角形时,m的值为_______.
11.如图,正方形ABCD中,点E,F分别在AD,CD上.且DE=CF,AF与BE相交于点G.若AB=4,DE=1,则GF的长 ____
12.如图,正方形和正方形的边长分别是4和6,且点,,在同一直线上,是线段的中点,连接,则的长为_________.
13.如图所示,以Rt△ABC的两直角边AC,BC分别作正方形ACED和正方形BCFG,连接EF;过点C作CH⊥AB于点H并反方向延长交EF于点I,若正方形ACED和正方形BCFG面积分别为16和9,则HI长为______.
14.如图,在正方形ABCD中,F在AB上,E在BC的延长线上,AF=CE,连接DF、DE、EF,EF交对角线BD于点N,M为EF的中点,连接MC,下列结论:①△DEF为等腰直角三角形;②∠FDB=∠FEC;③直线MC是BD的垂直平分线;④若BF=2,则MC=;其中正确结论的有_______.
三、解答题
15.问题情境:四边形中,点O是对角线的中点,点E是直线上的一个动点(点E与点C、O、A都不重合)过点A,C分别作直线的垂线,垂足分别为F、G,连接.
(1)初步探究:已知四边形是正方形,且点E在线段上,求证;
(2)探究图中与的数量关系,并说明理由.
16.如图,在四边形中,且,对角线和相交于点O,且,过点B作,交于点E,连结.
(1)求证:;
(2)试探究四边形的形状,并说明理由;
(3)若,,,求四边形的面积.
17.已知正方形如图所示,连接其对角线,的平分线交于点,过点作于点,交于点,过点作,交延长线于点P.
(1)求证:;
(2)若正方形的边长为4,求的面积;
(3)求证:.
18.(1)建立模型:如图1,在正方形中,E,F分别是上的点,且,探究图中线段之间的数量关系.小王同学探究此问题的方法是将绕A点逆时针旋转使得B与D重合,连接,由此得到______,再证明______,可得出线段之间的数量关系为______.
(2)拓展延伸:如图2,在等腰直角三角形中,,点G,H在边上,且,写出图中线段之间的数量关系并证明.
19.如图,四边形是正方形,点E是平面内异于点A的任意一点,以线段为边作正方形,连接.
(1)如图1,求证:;
(2)如图2,若点E在线段上,,,求的长.
20.如图1,在正方形中,E是边上的一动点(不与B重合),,,交于点G,连接.
(1)若,E为的中点,则 ;
(2)探究线段与的数量关系,并给出证明;
(3)如图2,连接,比较和的大小关系,并说明理由.
参考答案
1.解:∵四边形是正方形,
∴,
∵F、E分别是正方形的边与的中点,
∴,
∴,
∴,选项A正确,不符合题意;
∴,
又∵,
∴,
∴,,选项C正确,不符合题意:
由得,
∴,即,选项D正确:
只有选项B无法证明其成立,
故选B.
2.解:如图:
三个大小相同的正方形,
∵,,
又∵,
∴,即,
故选:C.
3.解:如图,过点E作EH⊥BC交AD于G,
∵四边形ABCD是正方形,
∴ADBC,∠ЕВН=∠ADB=45°,
∴四边形AGHB和四边形DGHC是矩形,△DGE是等腰直角三角形,
∴AG=BH=ЕН,DG=EG=1,
∴CH = DG= 1,
∵AG⊥GH,AE⊥EF,
∴∠AGE=∠AEF=∠FHE= 90°,
∴∠GAE+∠AEG=∠FEH+∠AEG= 90°,
∴∠GAE= ∠FEH,
∴△AGE≌△EHF(AAS),
∴GE= FH= 1,
∴CF= CH + FH= 2,
故选:A.
4.解:连接AG,延长AG交CD于M,连接FM,
∵四边形ABCD是正方形,
∴AB=CD=BC=AD=4,ABCD,∠C=90°,
∴∠AEG=∠GDM,∠EAG=∠DMG,
∵G为DE的中点,
∴GE=GD,
∴△AEG≌△MDG(AAS),
∴AG=MG,AE=DM=AB=CD,
∴CM=CD=2,
∵点H为AF的中点,
∴GH=FM,
∵F为BC的中点,
∴CF=BC=2,
∴FM=,
∴GH=FM=,
故选:C.
5.解:延长AD交EF于M,连接AC、CF,
∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=7,
∴AB=BC=1,CE=EF=7,∠E=90°,
则AM=BC+CE=1+7=8,FM=EF-AB=7-1=6,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH=AF,
在Rt△AMF中,由勾股定理得:,
∴CH=5,
故选:A.
6.解:连接PB,
∵正方形ABCD的面积为12,
∴AB=2,点B、D关于对角线AC对称,
∵△ABE是等边三角形,
∴AB=BE=2,
∵点B、D关于对角线AC对称,
∴PD=PB,
∴PD+PE的最小值即为BE的长,
即PD+PE的最小值为.
故选:C.
7.解:如图,过点作轴于点D,
∵四边形OABC是正方形,且OA=a,
∴A(0,a),
,
∵将正方形OABC绕点O顺时针旋转45°后得到正方形,
∴,
∴,
∴,
∴,
∴,
∵正方形绕点O顺时针旋转后得到正方形
∴,
∴,
同理,, ,,,,
……,
由此发现正方形旋转8次为一个循环,
∵2023÷8=252…7,
∴点A2023的坐标与相同,为.
故选:D
8.解:因为四边形ABCD是正方形,
所以OD=OC=OB=OA,
因为OE⊥CD,
根据等腰三角形三线合一,得DE=EC,
所以OE是△DBC的中位线,
所以OE= ,
故答案为:2.
9.解:如图,连接,,
点关于的对称点为点,
,
根据两点之间线段最短可得就是的最小值,
正方形的边长为3,,
,
的最小值是,
则△PEC周长的最小值为:
故答案为:.
10.解:如图1,当m=30°时,
BP=BC,△BPC是等腰三角形;
如图2,当m=60°时,
PB=PC,△BPC是等腰三角形;
如图3,当m=150°时,
PB=BC,△BPC是等腰三角形;
如图4,当m=300°时,
PB=PC,△BPC是等腰三角形;
综上所述,m的值为30°或60°或150°或300°,
故答案为:30°或60°或150°或300°.
11.解:∵四边形形ABCD是正方形,
∴AB=AD=DC,∠BAD=∠D=90°,
又∵DE=CF,
∴AE=DF,
∴在△BAE和△ADF中,
,
∴△BAE≌△ADF(SAS).
∴∠ABE=∠DAF,BE=AF,
∵∠DAF+∠BAG=90°,
∴∠ABE+∠BAG=90°,
∴∠AGB=90°,
∴BE⊥AF.
∵AB=AD=4,DE=1,
∴AE=AD-DE=3,
∴在Rt△ABE中,有,
∴AF=BE=5,
∵BE⊥AF,∠BAD=90°,
∴,
∴,
∴,
故答案为:.
12.解:延长AD至H,延长FM与AH交于H点,
由题意可得ADEF,
∴,
∵是线段的中点,
∴,
∴在△AMH和△EMF中,
∴△AMH≌△EMF,
即FM=MH,AH=EF,
∴DH=AH-AD=EF-AD=2,
∵DF=CF-CD=6-4=2,
在直角△DFH中,FH为斜边,
∴FH=,
∵FM=MH,
∴FM=.
故答案为:.
13.解:∵正方形ACED和正方形BCFG面积分别为16和9,
∴,
中,,
依题意,,
∴,
∴,
∵,
∴,
又,
∴,
∴,
同理可得,
∴,
,
,
∴.
故答案为:4.9.
14.解:四边形是正方形,
,
在和中,,
,
,
,
为等腰直角三角形,结论①正确;
,
又,
,
即,结论②正确;
如图,连接,
为和斜边上的中点,
,
又,
直线是的垂直平分线,结论③正确;
如图,取的中点,连接,
,
,
直线是的垂直平分线,,
(等腰三角形的三线合一),
是等腰直角三角形,且,
,结论④正确;
综上,正确结论的有①②③④,
故答案为:①②③④.
15.(1)证明:∵四边形是正方形,
∴,
∵,
∴,
∴,
在和中,,
∴,
∴;
(2)解:,理由如下:
如图,延长交于H,
∵,
∴,
∴,
∵,
在和中,
,
∴,
∴,
在中,.
∴.
16.(1)证明:∵,
∴,
在和中,
∵,
∴;
(2)解:四边形是矩形,理由如下:
∵,
∴,
∵,
∴四边形是平行四边形,
∵,
∴四边形是矩形;
(3)解:∵且,
∴,即,
∴四边形是正方形,
∴,
设,则,
在中,由勾股定理得,即,
解得:,(舍去),
∴,
∴,
∴,
∴四边形的面积为18.
17.(1)解:证明:四边形是正方形,
,,
,
,
,
,,
,
;
(2)平分,
,
,
,
,且,
,
,
,
;
(3)在上截取,连接,
,
,
,且,
,
,
,
,
,,
,
,
,
.
18.解:(1)∵四边形是正方形,
∴,
由旋转的性质可知:,
∵,
∴,
∴,
∵,
∴三点共线,
又∵,
∴,
∴,
∵,
∴.
故答案为:;;.
(2),证明如下:
如图所示,将绕点B逆时针旋转得到.
∵,
∴,
由旋转的性质可知:,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
19.(1)证明:∵四边形和四边形都是正方形,
∴,
∴,
在△AGD和△AEB中,
,
∴,
∴;
(2)解:作于H,
∵四边形和四边形都是正方形,
∴,.
由勾股定理得,
∴,
∴,
∴.
20.(1)解:在正方形中,,
∵E为的中点,,
∴,
∴,
故答案为:
(2)解:.
在线段上截取,连接
∵
∴
∴
∵在正方形中
∴
∴
∵
∴
∴
∴
∵,,
∴
∴,
∵在中,
∴
∴;
(3)解:延长至P,使得,连接
∵在正方形中
∴,
∴
∵,,
∴
∴,
∵,
∴
∴
∴
即
∵,,
∴
∴
又∵,
∴.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
