沪科版八年级三角形全等的判定(SSS)
文档属性
| 名称 | 沪科版八年级三角形全等的判定(SSS) |  | |
| 格式 | zip | ||
| 文件大小 | 254.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-02 16:18:06 | ||
图片预览



文档简介
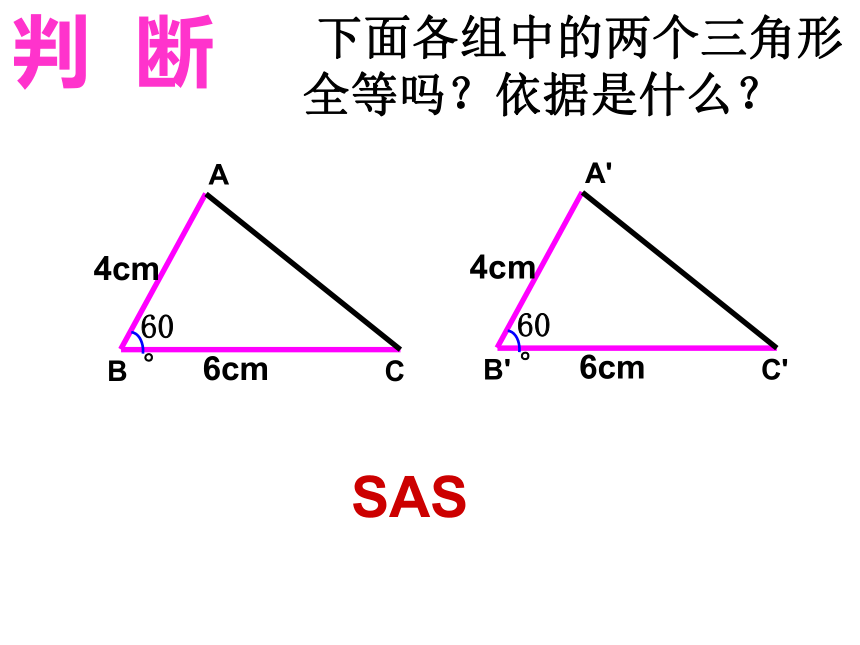
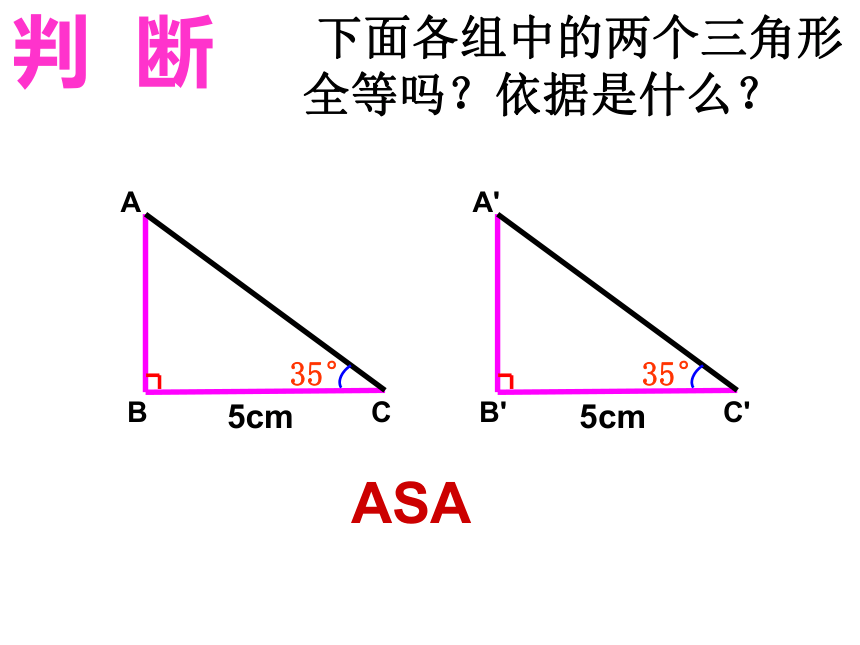
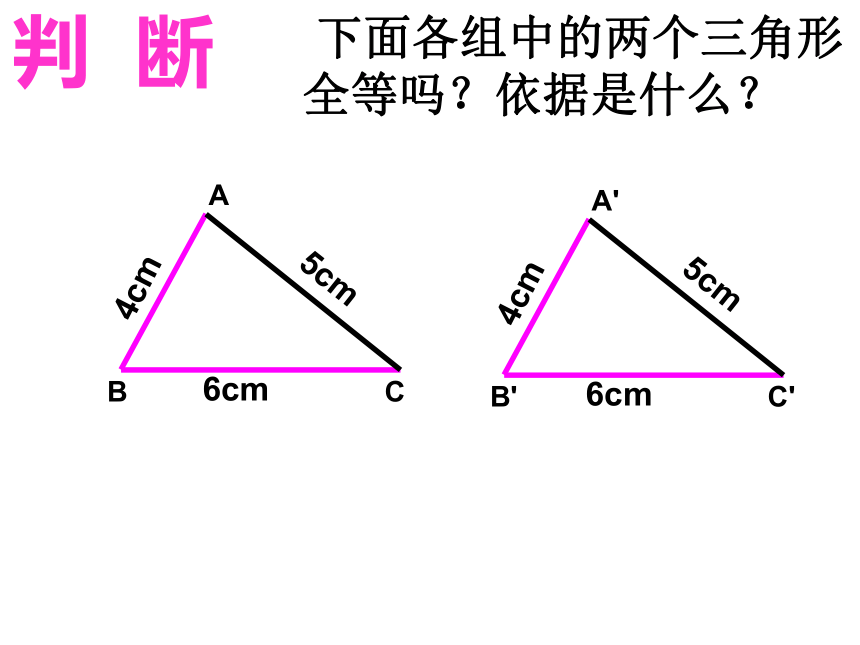
课件17张PPT。沪科版八年级(上册)14.2 全等三角形的判定(第四课时)安庆市白泽湖中学 郑玉兵判定方法1: 两边及其夹角对应相等的两个三角形全等.(边角边)(SAS)复习回顾判定方法2:两角及其夹边对应相等的两个三角形全等. (角边角)(ASA) 我们已经学习了几种三角形全等的判定方法? 下面各组中的两个三角形全等吗?依据是什么?SAS判 断 下面各组中的两个三角形全等吗?依据是什么?ASA判 断 下面各组中的两个三角形全等吗?依据是什么?判 断3.连接线段A′B,A′C′.已知:△ABC,
求做:△A′B′C′,使A′B′=AB,B′C′=BC,
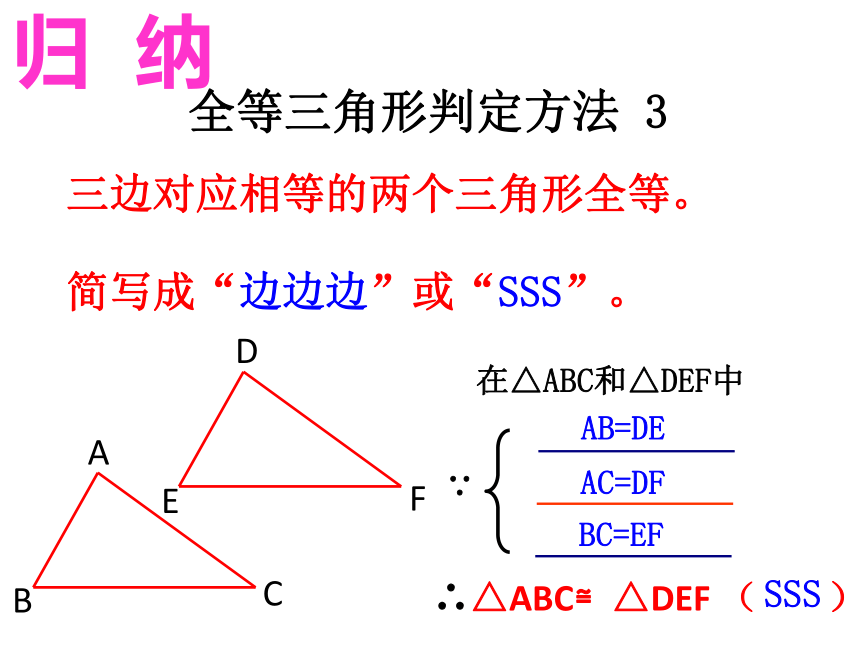
C′A′=CA.2.分别以B′、C′为圆心,线段BA、CA的长为半径画弧,两弧交于点A′;1.作线段B′C′=BC;则△A′B′C′就是所求作的三角形探究 所画的△A′B′C′与△ABC一定全等吗?归 纳全等三角形判定方法 3三边对应相等的两个三角形全等。
简写成“边边边”或“SSS”。∴△ABC≌△DEF ( )SSSAB=DEAC=DFBC=EF 三角形稳定性,在日常生活和实际生产中有着广泛的应用. 上面结论说明,只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定,这个性质叫做三角形的稳定性。已知:如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF ,BE=CF。求证:AB∥DE,AC∥DF分析:回忆我们学习过哪些证明两条直线
平行的方法. 而要证∠ B= ∠ DEF, ∠ACB= ∠ F ,可转化成证△ABC≌△DEF 转化成证∠ B= ∠ DEF,
∠ACB= ∠ F本例中,要证AB∥DE,
AC∥DF例题 ∴∠B= ∠DEF,∠ACB=∠F (全等三角形的对应角相等)∴AB∥DE,AC∥DF(同位角相等,两直线平行)证明:∵BE=CF(已知)∴BE+EC =CF+EC (等式性质)即 BC=EF例题 ∴ △ABD ≌ △ABC ( SSS) AB=DE ( )
AC=DF ( )
BC=EF ( 已证 )已知:如图,点B、E、C、F在同一条
直线上,AB=DE,AC=DF ,BE=CF。
求证:AB∥DE,AC∥DF练习课本p105 练习第1、2、3题挑战已知:如图.AB = DC , AC = DB,
求证:∠A = ∠D
本节课你有什么收获?2.掌握三角形的判定方法“SSS”;1.知道三角形三条边的长度怎样画三角形;3.了解三角形的稳定性。作业同步练习P77~78
基础练习14.2(三)第1~9题作业要认真完成哟!
求做:△A′B′C′,使A′B′=AB,B′C′=BC,
C′A′=CA.2.分别以B′、C′为圆心,线段BA、CA的长为半径画弧,两弧交于点A′;1.作线段B′C′=BC;则△A′B′C′就是所求作的三角形探究 所画的△A′B′C′与△ABC一定全等吗?归 纳全等三角形判定方法 3三边对应相等的两个三角形全等。
简写成“边边边”或“SSS”。∴△ABC≌△DEF ( )SSSAB=DEAC=DFBC=EF 三角形稳定性,在日常生活和实际生产中有着广泛的应用. 上面结论说明,只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定,这个性质叫做三角形的稳定性。已知:如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF ,BE=CF。求证:AB∥DE,AC∥DF分析:回忆我们学习过哪些证明两条直线
平行的方法. 而要证∠ B= ∠ DEF, ∠ACB= ∠ F ,可转化成证△ABC≌△DEF 转化成证∠ B= ∠ DEF,
∠ACB= ∠ F本例中,要证AB∥DE,
AC∥DF例题 ∴∠B= ∠DEF,∠ACB=∠F (全等三角形的对应角相等)∴AB∥DE,AC∥DF(同位角相等,两直线平行)证明:∵BE=CF(已知)∴BE+EC =CF+EC (等式性质)即 BC=EF例题 ∴ △ABD ≌ △ABC ( SSS) AB=DE ( )
AC=DF ( )
BC=EF ( 已证 )已知:如图,点B、E、C、F在同一条
直线上,AB=DE,AC=DF ,BE=CF。
求证:AB∥DE,AC∥DF练习课本p105 练习第1、2、3题挑战已知:如图.AB = DC , AC = DB,
求证:∠A = ∠D
本节课你有什么收获?2.掌握三角形的判定方法“SSS”;1.知道三角形三条边的长度怎样画三角形;3.了解三角形的稳定性。作业同步练习P77~78
基础练习14.2(三)第1~9题作业要认真完成哟!
