人教A版必修二8.5.1直线与直线平行 课件(共16张PPT)
文档属性
| 名称 | 人教A版必修二8.5.1直线与直线平行 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 502.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-19 06:24:42 | ||
图片预览





文档简介
(共16张PPT)
高中数学一年级
8.5 空间直线、平面的平行
在平面几何的学习中,我们研究过两条直线的位
置关系,重点研究了两条直线平行,得到了两条直线
平行的性质,以及判定两条直线平行的定理。类似地,
空间中直线、平面间的平行关系在生产和生活中有着
广泛的应用,也是我们要重点研究的内容。本节我们
研究空间中直线、平面的平行关系,重点研究这些
平行关系的判定和性质。
8.5.1 直线与直线平行
问题1.判断下列命题的真假
在同一平面内,如果两条直线没有公共点,则两直线平行。
过直线外一点有且只有一条直线和已知直线平行。
在同一平面内,如果两条直线都和第三条直线平行,则这两条直线平行。
1
(一)情境引入
在空间中是否正确?
真
真
真
观察长方体的侧棱有什么关系?图片中的直线间的位置关系是什么?观察房间,哪些直线是平行?
观
察
思
考
动手
实验
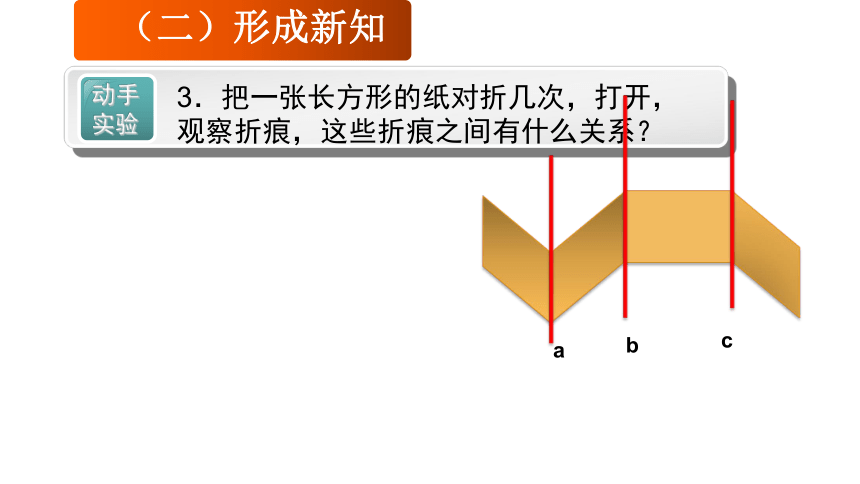
3.把一张长方形的纸对折几次,打开,观察折痕,这些折痕之间有什么关系?
(二)形成新知
a
b
c
基本事实4:平行于同一条直线的两条直线互相平行(通常称为平行线的传递性)
(二)形成新知
a b c
若a// b,b// c则a//c
基本事实4是判断证明空间中两直线平行的重要
依据。
(三)公理应用
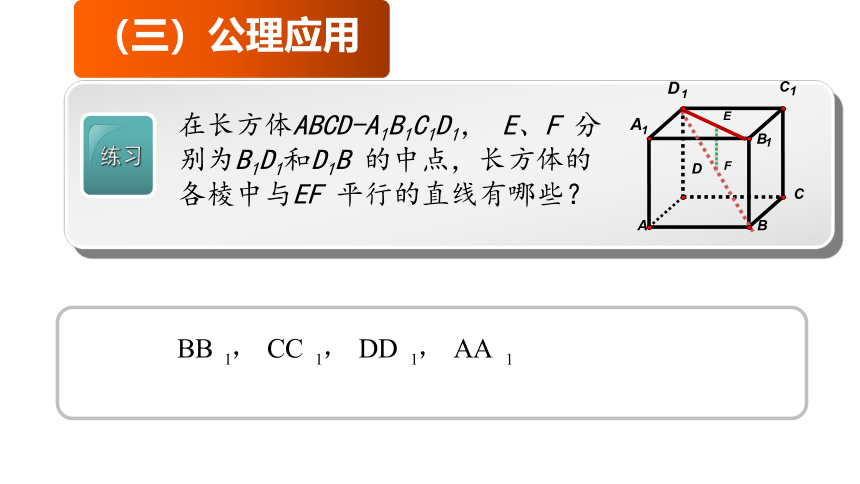
练习
在长方体ABCD-A1B1C1D1, E、F 分别为B1D1和D1B 的中点,长方体的各棱中与EF 平行的直线有哪些?
F
E
C
D
B
A
D
1
A
1
B
1
C
1
F
G
H
E
A
B
D
C
(三)公理应用
例1
在空间四边形ABCD中,E、F、G、H分别是棱AB 、BC、CD、DA的中点
求证:四边形EFGH是平行四边形。
证明:在△ABD中,因为E,H分别是AB,AD的中点,
所以EH//BD,EH= BD,
同理,FG//BD,FG= BD,
所以EH//FG,EH=FG,
所以四边形EFGH是平行四边形。
变式:例1条件不变,若对角线AC=BD,四边形EFGH什么图形?
菱形
(三)公理应用
空间中两直线平行的证明方法:
1.利用定义:证明两条直线共面且无公共点。
2.利用平面几何知识(三角形、梯形的中位线,平行四边形的性质、平行线分线段成比例定理等)证明。
3.利用基本事实4,即找到第三条直线c,使a//c,b//c,从而得到a//b。
如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等。
(三)公理应用
问题4
在平面几何中我们学过等角定理 “如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等。” 在空间中是否成立?
B
A C
B1
A1 C1
D1
E1
D
E
如何对结论进行证明
5
证明两角相等的常用方法有哪些?
(三)公理应用
如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等。
已知:∠BAC和∠B1A1C1的边AB//A1B1,AC//A1C1,且射线AB与A1B1同向,射线AC与A1C1同向
求证:∠BAC=∠B1A1C1
B1
A1 C1
D1
E1
D
E
B
A C
分析:为证明∠BAC=∠B1A1C1,我们构造两个全等三角形.
(三)公理应用
证明:对于∠BAC和∠B1A1C1在同一个平面内的情形,在初中几何中已经证明,
下面证明两个角不在同一平面内的情形。
分别在∠BAC的两边和∠B1A1C1的两边上截取线段AD=A1D和AE=A1E1.
因为AD // A1D1 所以AA1D1D 是平行四边形,
所以AA1 // DD1 同理可得AA1 // EE1
所以DD1E1E是平行四边形。所以EE1 // DD1
在△ADE和△A1D1E1中,
AD=A1D1,AE=A1E1,DE=D1E1,
于是△ADE≌△A1D1E1,
所以∠BAC=∠B1A1C1
D1
E1
D
E
B
A C
B1
A1 C1
等角定理:如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等。
(三)公理应用
思考
讨论
6.如果一个角的两边与另一个角的两边分别对应平行,那么这两个角的关系又如何呢?
结论1 若空间中两个角的两边分别对应平行,且方向都相同(或方向都相反),则这两个角相等。
结论2 若空间中两个角的两边分别对应平行,且一组对应边方向相同,另一组对应边方向相反,则这两个角互补。
(三)公理应用
定理:如果空间中两个角的两边分别对应平行,那么这两个角相等或互补。
练习:若OA//O'A',OB//O'B',且∠AOB=1300, 则∠A'O'B'=
1300
或500
反思2
提高
本节课你学习了什么?
你发现了什么?
有什么收获?
还有什么问题?
(四)归纳总结
1. 完成课本135页 练习
2. 预习8.5.2
作业
(五)布置作业
高中数学一年级
8.5 空间直线、平面的平行
在平面几何的学习中,我们研究过两条直线的位
置关系,重点研究了两条直线平行,得到了两条直线
平行的性质,以及判定两条直线平行的定理。类似地,
空间中直线、平面间的平行关系在生产和生活中有着
广泛的应用,也是我们要重点研究的内容。本节我们
研究空间中直线、平面的平行关系,重点研究这些
平行关系的判定和性质。
8.5.1 直线与直线平行
问题1.判断下列命题的真假
在同一平面内,如果两条直线没有公共点,则两直线平行。
过直线外一点有且只有一条直线和已知直线平行。
在同一平面内,如果两条直线都和第三条直线平行,则这两条直线平行。
1
(一)情境引入
在空间中是否正确?
真
真
真
观察长方体的侧棱有什么关系?图片中的直线间的位置关系是什么?观察房间,哪些直线是平行?
观
察
思
考
动手
实验
3.把一张长方形的纸对折几次,打开,观察折痕,这些折痕之间有什么关系?
(二)形成新知
a
b
c
基本事实4:平行于同一条直线的两条直线互相平行(通常称为平行线的传递性)
(二)形成新知
a b c
若a// b,b// c则a//c
基本事实4是判断证明空间中两直线平行的重要
依据。
(三)公理应用
练习
在长方体ABCD-A1B1C1D1, E、F 分别为B1D1和D1B 的中点,长方体的各棱中与EF 平行的直线有哪些?
F
E
C
D
B
A
D
1
A
1
B
1
C
1
F
G
H
E
A
B
D
C
(三)公理应用
例1
在空间四边形ABCD中,E、F、G、H分别是棱AB 、BC、CD、DA的中点
求证:四边形EFGH是平行四边形。
证明:在△ABD中,因为E,H分别是AB,AD的中点,
所以EH//BD,EH= BD,
同理,FG//BD,FG= BD,
所以EH//FG,EH=FG,
所以四边形EFGH是平行四边形。
变式:例1条件不变,若对角线AC=BD,四边形EFGH什么图形?
菱形
(三)公理应用
空间中两直线平行的证明方法:
1.利用定义:证明两条直线共面且无公共点。
2.利用平面几何知识(三角形、梯形的中位线,平行四边形的性质、平行线分线段成比例定理等)证明。
3.利用基本事实4,即找到第三条直线c,使a//c,b//c,从而得到a//b。
如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等。
(三)公理应用
问题4
在平面几何中我们学过等角定理 “如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等。” 在空间中是否成立?
B
A C
B1
A1 C1
D1
E1
D
E
如何对结论进行证明
5
证明两角相等的常用方法有哪些?
(三)公理应用
如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等。
已知:∠BAC和∠B1A1C1的边AB//A1B1,AC//A1C1,且射线AB与A1B1同向,射线AC与A1C1同向
求证:∠BAC=∠B1A1C1
B1
A1 C1
D1
E1
D
E
B
A C
分析:为证明∠BAC=∠B1A1C1,我们构造两个全等三角形.
(三)公理应用
证明:对于∠BAC和∠B1A1C1在同一个平面内的情形,在初中几何中已经证明,
下面证明两个角不在同一平面内的情形。
分别在∠BAC的两边和∠B1A1C1的两边上截取线段AD=A1D和AE=A1E1.
因为AD // A1D1 所以AA1D1D 是平行四边形,
所以AA1 // DD1 同理可得AA1 // EE1
所以DD1E1E是平行四边形。所以EE1 // DD1
在△ADE和△A1D1E1中,
AD=A1D1,AE=A1E1,DE=D1E1,
于是△ADE≌△A1D1E1,
所以∠BAC=∠B1A1C1
D1
E1
D
E
B
A C
B1
A1 C1
等角定理:如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等。
(三)公理应用
思考
讨论
6.如果一个角的两边与另一个角的两边分别对应平行,那么这两个角的关系又如何呢?
结论1 若空间中两个角的两边分别对应平行,且方向都相同(或方向都相反),则这两个角相等。
结论2 若空间中两个角的两边分别对应平行,且一组对应边方向相同,另一组对应边方向相反,则这两个角互补。
(三)公理应用
定理:如果空间中两个角的两边分别对应平行,那么这两个角相等或互补。
练习:若OA//O'A',OB//O'B',且∠AOB=1300, 则∠A'O'B'=
1300
或500
反思2
提高
本节课你学习了什么?
你发现了什么?
有什么收获?
还有什么问题?
(四)归纳总结
1. 完成课本135页 练习
2. 预习8.5.2
作业
(五)布置作业
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
