第二十二章 二次函数单元测试题(含答案)
文档属性
| 名称 | 第二十二章 二次函数单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-19 18:46:44 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十二章 二次函数单元测试 人教版数学 九年级上册
一、选择题(共8题,每题3分,满分24分)
1.如图,抛物线 与 轴只有一个公共点A(1,0),与 轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为( )
A.1 B.2 C.3 D.4
2.已知二次函数的图象(0≤x≤4)如图,关于该函数在所给自变量的取值范围内,下列说法正确的是( )
A.有最大值2,有最小值-2.5 B.有最大值2,有最小值1.5
C.有最大值1.5,有最小值-2.5 D.有最大值2,无最小值
3.已知关于x的不等式组 有解,则a的取值不可能是( )
A.0 B.1 C.2 D.-2
4.若点 在第二象限,则点 在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
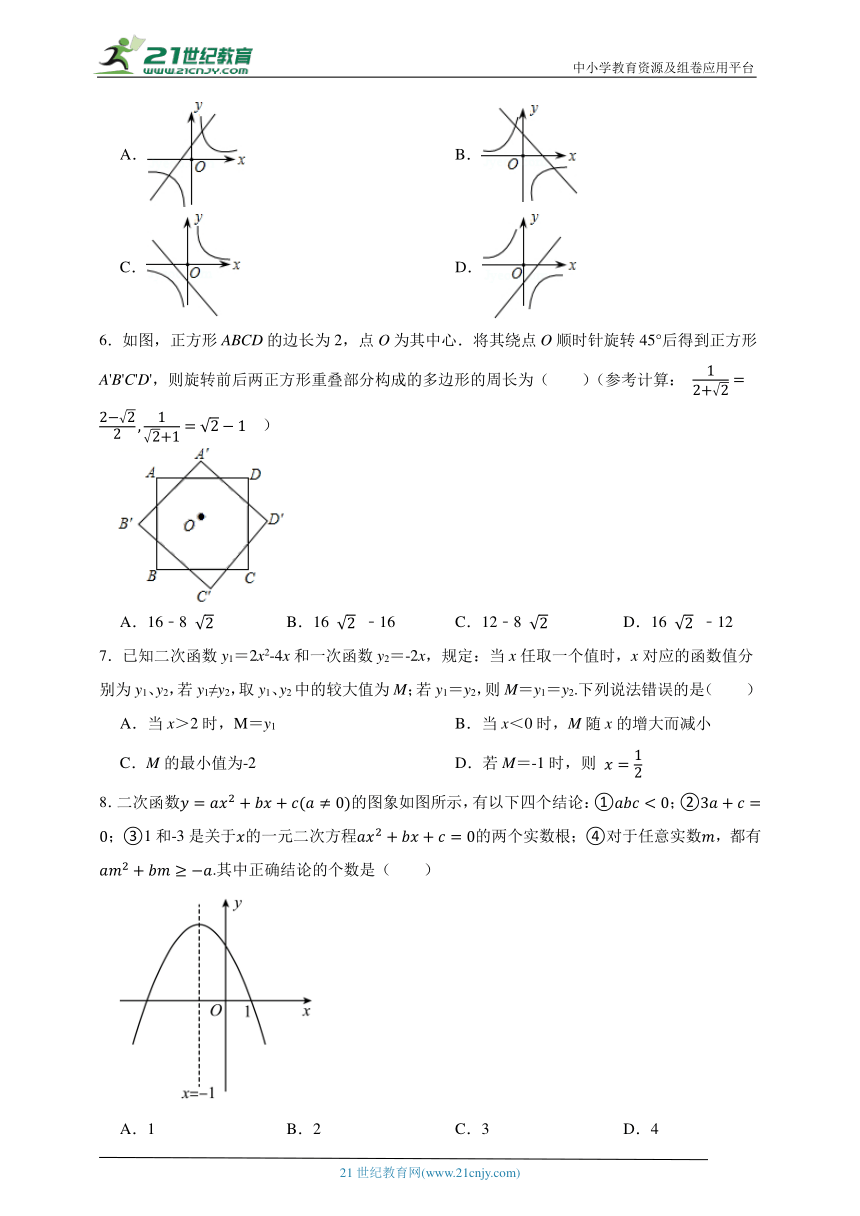
5.函数y=﹣ax+a与y= (a≠0)在同一坐标系中的图象可能是( )
A. B.
C. D.
6.如图,正方形ABCD的边长为2,点O为其中心.将其绕点O顺时针旋转45°后得到正方形A'B'C'D',则旋转前后两正方形重叠部分构成的多边形的周长为( )(参考计算: )
A.16﹣8 B.16 ﹣16 C.12﹣8 D.16 ﹣12
7.已知二次函数y1=2x2-4x和一次函数y2=-2x,规定:当x任取一个值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较大值为M;若y1=y2,则M=y1=y2.下列说法错误的是( )
A.当x>2时,M=y1 B.当x<0时,M随x的增大而减小
C.M的最小值为-2 D.若M=-1时,则
8.二次函数的图象如图所示,有以下四个结论:①;②;③1和-3是关于的一元二次方程的两个实数根;④对于任意实数,都有.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(共5题,每题3分,满分15分)
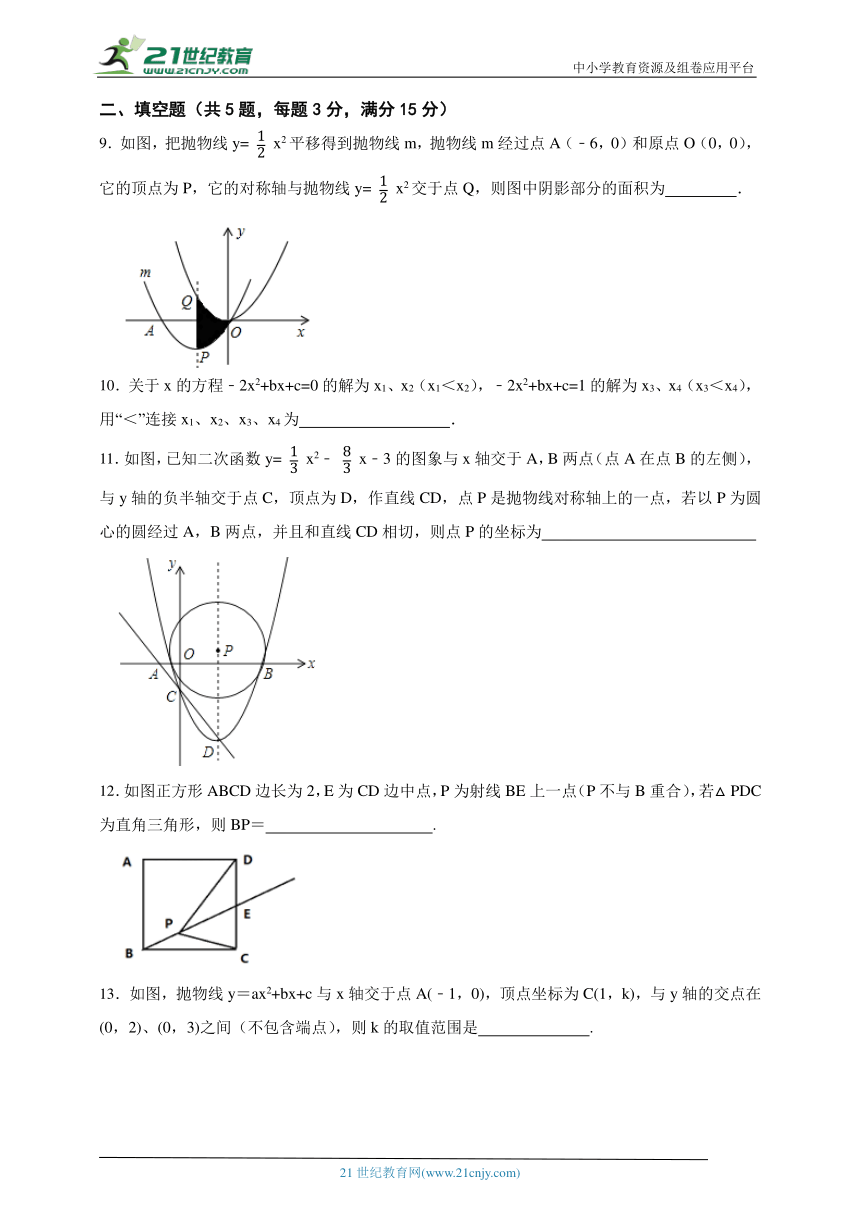
9.如图,把抛物线y= x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为 .
10.关于x的方程﹣2x2+bx+c=0的解为x1、x2(x1<x2),﹣2x2+bx+c=1的解为x3、x4(x3<x4),用“<”连接x1、x2、x3、x4为 .
11.如图,已知二次函数y= x2﹣ x﹣3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为
12.如图正方形ABCD边长为2,E为CD边中点,P为射线BE上一点(P不与B重合),若△PDC为直角三角形,则BP= .
13.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为C(1,k),与y轴的交点在(0,2)、(0,3)之间(不包含端点),则k的取值范围是 .
三、解答题(共7题,满分81分)
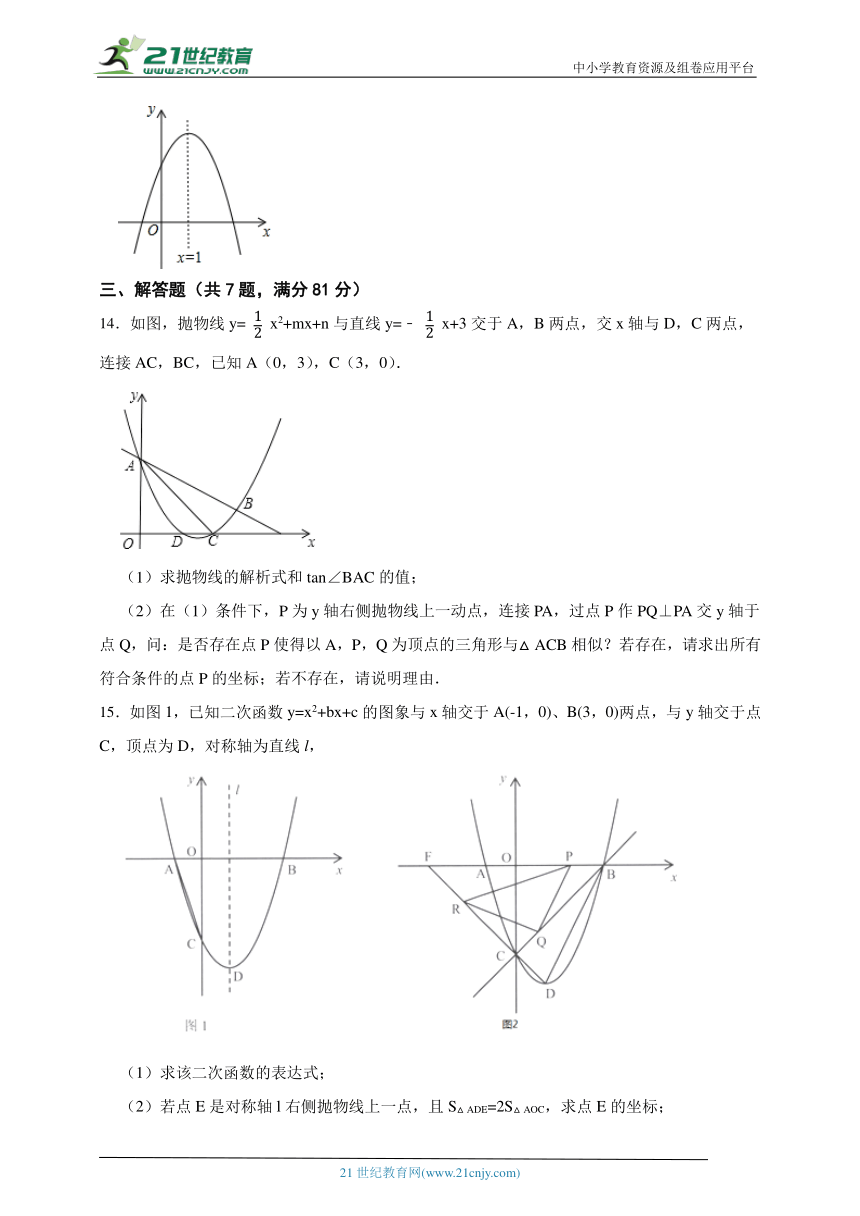
14.如图,抛物线y= x2+mx+n与直线y=﹣ x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
(1)求抛物线的解析式和tan∠BAC的值;
(2)在(1)条件下,P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
15.如图1,已知二次函数y=x2+bx+c的图象与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为D,对称轴为直线l,
(1)求该二次函数的表达式;
(2)若点E是对称轴l右侧抛物线上一点,且S△ADE=2S△AOC,求点E的坐标;
(3)如图2,连接DC并延长交x轴于点F,设P为线段BF上一动点(不与B、F重合),过点P作PQ BD交直线BC于点Q,将直线PQ绕点P沿顺时针方向旋转45 后,所得的直线交DF于点R,连接OR.请直接写出当△PQR与△PFR相似时点P的坐标.
16.如图所示,已知抛物线经过点A(-2,0)、B(4,0)、C(0,-8),抛物线y=ax2+bx+c(a≠0)与直线y=x-4交于B,D两点.
(1)求抛物线的解析式并直接写出D点的坐标;
(2)点P为抛物线上的一个动点,且在直线BD下方,试求出△BDP面积的最大值及此时点P的坐标;
(3)点Q是线段BD上异于B、D的动点,过点Q作QF⊥x轴于点F,交抛物线于点G.当△QDG为直角三角形时,求点Q的坐标.
四、综合题
17.在直角坐标系xOy中,定义点C(a,b)为抛物线L:y=ax2+bx(a≠0)的特征点坐标.
(1)已知抛物线L经过点A(﹣2,﹣2)、B(﹣4,0),求出它的特征点坐标;
(2)若抛物线L1:y=ax2+bx的位置如图所示:
①抛物线L1:y=ax2+bx关于原点O对称的抛物线L2的解析式为 ;
②若抛物线L1的特征点C在抛物线L2的对称轴上,试求a、b之间的关系式;
③在②的条件下,已知抛物线L1、L2与x轴有两个不同的交点M、N,当一点C、M、N为顶点构成的三角形是等腰三角形时,求a的值.
18.如图,正方形 ,点 在边 上, 为等腰直角三角形.
(1)如图1,当 ,求证 ;
(2)如图2,当 ,取 的中点 ,连接 ,求证:
19.小明在学完了平行四边形后,想对“四边形的不稳定性”和“四边形的判定”有更好的理解,做了如下的探究:他用8根木棍和一些钉子组成了正方形和平行四边形(如图1),且,在同一条直线上,点落在边上.经小明测量,发现此时、、三个点在一条直线上,,.
(1)求的长.
(2)设的长度为,则 (用含的代数式表示).
(3)小明接着探究,在保证,位置不变的前提条件下,从点向右推动正方形,直到四边形刚好变为矩形时停止推动(如图2).若此时,求的长.
20.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c(a<0)经过点A(-1,0)、B(4,0)与y轴交于点C,tan∠ABC= .
(1)求抛物线的解析式;
(2)点M在第一象限的抛物线上,ME平行y轴交直线BC于点E,连接AC、CE,当ME取值最大值时,求△ACE的面积.
(3)在y轴负半轴上取点D(0,-1),连接BD,在抛物线上是否存在点N,使∠BAN=∠ACO-∠OBD?若存在,请求出点N的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】C
4.【答案】C
5.【答案】D
6.【答案】B
7.【答案】D
8.【答案】B
9.【答案】
10.【答案】x1<x3<x4<x2
11.【答案】(4,0)或(4, )
12.【答案】 或 或
13.【答案】 <k<4
14.【答案】解:(1)把A(0,3),C(3,0)代入y= x2+mx+n,得
,
解得: .
∴抛物线的解析式为y= x2﹣ x+3.
联立 ,
解得: 或 ,
∴点B的坐标为(4,1).
过点B作BH⊥x轴于H,如图1.∵C(3,0),B(4,1),
∴BH=1,OC=3,OH=4,CH=4﹣3=1,∴BH=CH=1.
∵∠BHC=90°,∴∠BCH=45°,BC= .
同理:∠ACO=45°,AC=3 ,
∴∠ACB=180°﹣45°﹣45°=90°,
∴tan∠BAC= ;
(2)存在点P,使得以A,P,Q为顶点的三角形与△ACB相似.
过点P作PG⊥y轴于G,
则∠PGA=90°.
设点P的横坐标为x,由P在y轴右侧可得x>0,则PG=x.
∵PQ⊥PA,∠ACB=90°,∴∠APQ=∠ACB=90°.
若点G在点A的下方,
①如图2①,当∠PAQ=∠CAB时,则△PAQ∽△CAB.
∵∠PGA=∠ACB=90°,∠PAQ=∠CAB,∴△PGA∽△BCA,
∴ .
∴AG=3PG=3x.
则P(x,3﹣3x).把P(x,3﹣3x)代入y= x2﹣ x+3,得: x2﹣ x+3=3﹣3x,
整理得:x2+x=0,解得:x1=0(舍去),x2=﹣1(舍去).
②如图2②,
当∠PAQ=∠CBA时,则△PAQ∽△CBA.
同理可得:AG= PG= x,则P(x,3﹣ x),
把P(x,3﹣ x)代入y= x2﹣ x+3,得: x2﹣ x+3=3﹣ x,
整理得:x2﹣ x=0,解得:x1=0(舍去),x2= ,∴P( , );
若点G在点A的上方,
①当∠PAQ=∠CAB时,则△PAQ∽△CAB,
同理可得:点P的坐标为(11,36).
②当∠PAQ=∠CBA时,则△PAQ∽△CBA.
同理可得:点P的坐标为P( , ).
综上所述:满足条件的点P的坐标为(11,36)、( , )、( , ).
15.【答案】(1)解:将A(-1,0)、B(3,0)代入二次函数y=x2+bx+c,得
解得
则二次函数为y=x2-2x-3.
(2)解:设E(m,m2–2m–3),过点E作EM//x轴,交AD于点M,
由二次函数为y=x2-2x-3,可得C(0,-3),D(1,-4),
则S△ADE=S△AOC=2× ×3×1=3.
∵A(–1,0)、D(1,–4)
∴直线AD为:y=–2x–2,
∵E(m,m2–2m–3),
∴M( m2+m+ ,m2–2m–3),
∴EM= m-( m2+m+ )= m2 ,
∴S△ADE= ×4EM=2EM= m2-1=3,
解得m=±2(其中m =–2舍去),
∴E(2–3).
(3)解:由B(3,0)和C(0,-3)可得直线BC为y=x-3,
由B(3,0)和D(1,-4)可得直线BD为y=2x-6,
设P(n,0),因为PQ//BD,则可设PQ为y=2(x-n),
联立
解得
则Q(2n-3,2n-6),
由C(0,-3)和D(1,-4)可得直线CD为y=-x-3,则F(-3,0),
所以OF=OC,则∠OFR=45°,
则∠RPQ=∠OFR=45°.
当△QPR与△PFR时,有△RPQ~△PFR和△QPR~△PFR两种情况:
①当△RPQ~△PFR时,∠QRP=∠RPF,则RQ//x轴,则点R的纵坐标与点Q相等,
当y=2n-6代入直线CD可解得x=-2n+3,R(-2n+3,2n-6),
即RQ=2n-3-(-2n+3)=4n-6,RP2= ,
又PF=3+n,因为 ,
所以RP2=PF·RQ,
即 =(3+n)(4n-6),
化简得9n2-48n+63=0,
即(3n-7)(3n-9)=0,
解得n= 或n=3(舍去);
当n= 时,P1( ,0);
②当△QPR~△PFR时,∠PRQ=∠FRP,P2(0,0).
综上,P1( ),P2(0,0).
16.【答案】(1)设抛物线的解析式为y=ax2+bx+c∵抛物线经过点A(-2,0)、B(4,0)、C(0,-8)∴,解得.
∴抛物线的解析式为y=x2-2x-8
点D的坐标为(-1,-5)
(2)过P作PE∥y轴,交直线AB于点E
设P(x,x2-2x-8)则E(x,x-4)
∴PE=x-4-(x2-2x-8)=-x2+3x+4
∴S△BDP=S△DEP+S△BEP= PE·(xE-xD)+ PE·(xB-xE)
= PE·(xB-xD)= PE= (-x2+3x+4)
=- (x- )2+
∴当x= 时,△BDP面积的最大值为
此时点P的坐标为( ,- )
(3)设直线y=x-4与y轴相交于点K,则K(0,-4)∵B(4,0),∴OB=OK=4,∴∠OKB=∠OBK=45°
∵QF⊥x轴,∴∠DQG=45°
若△QDG为直角三角形,则△QDG是等腰直角三角形①∠QDG=90°,过D作DH⊥QG于H,∴QG=2DH,
∴-x2+3x+4=2(x+1),解得x 1=-1(舍去),
x 2=2,∴Q1(2,-2)
②∠DGQ=90°,则DH=QH,∴-x2+3x+4=x+1,解得x 1=-1(舍去),x 2=3,∴P2(3,-1)综上所述,当△QDG为直角三角形时,点Q的坐标为(2,-2)或(3,-1)
17.【答案】(1)解:将点A(﹣2,﹣2)、B(﹣4,0)代入到抛物线解析式中,得
,解得: .∴抛物线L的解析式为 ,
∴它的特征点为( ,2).
(2)y=﹣ax2+bx;解:②∵抛物线L2的对称轴为直线:x= .∴当抛物线L1的特征点C(a,b)在抛物线L2的对称轴上时,有a= ,∴a与b的关系式为b=2a2. ③∵抛物线L1、L2与x轴有两个不同的交点M、N,∴在抛物线L1:y=ax2+bx中,令y=0,即ax2+bx=0,解得:x1= ,x2=0(舍去),即点M( ,0);在抛物线L2:y=﹣ax2+bx中,令y=0,即﹣ax2+bx=0,解得:x1= ,x2=0(舍去),即点N( ,0).∵b=2a2,∴点M(﹣2a,0),点N(2a,0),点C(a,2a2).∴MN=2a﹣(﹣2a)=4a,MC= ,NC= .因此以点C、M、N为顶点的三角形是等腰三角形时,有以下三种可能:(1)MC=MN,此时有: =4a,即9a2+4a4=16a2,解得:a=0,或a= ,∵a<0,∴a= ;(2)NC=MN,此时有: =4a,即a2+4a4=16a2,解得:a=0,或a= ,∵a<0,∴a= ;(3)MC=NC,此时有: = ,即9a2=a2,解得:a=0,又∵a<0,∴此情况不存在.综上所述:当以点C、M、N为顶点的三角形是等腰三角形时,a的值为 或 .
18.【答案】(1)证明:作 ,
四边形 是正方形
是等腰直角三角形
(2)连接 ,在 上截取 ,使得 ,连接 ,
为等腰直角三角形,
四边形 是正方形
三点共线
为 的中点,
在 中,
即
19.【答案】(1)解:∵四边形是平行四边形,
∴,,
∴.
∵四边形是正方形,
∴,,
∴,
∴,
∴,
∴,
∴,
∴
(2)
(3)解:∵在推动过程中,位置不变,的长度保持不变,
∴设,则.
∵四边形是矩形,
∴,,
∴,
∴.
∴,
∵,解得,
,,
∴.
20.【答案】(1)解:∵B(4,0),
∴OB=4,
∵tan∠ABC= = = ,
∴OC=2,
∴C(0,2),
设y=a(x-1)(x-4),
把C(0,2)代入,得a=- ,
∴抛物线的解析式为y=- (x-1)(x-4)=- x2+ x+2;
(2)解:设直线BC的解析式为y=kx+2,
把B(4,0)代入,得k=- ,
∴直线BC解析式为y=- x+2,
设M(m,- m2+ m+2),
则E(m,- m+2),
∴ME=- m2+2m,
∴当m=2时,ME取得最大值2,
∴E(2,1),
∴S△ACE=S△ABC-S△ABE= ×5×(2-1)= ;
(3)解:作C′(0,-2)与 C关于x轴对称,连接BC′,过点D作DE⊥BC′于点E,
∴∠ABC=∠ABC′,
∵ = ,∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴∠ABC=∠ACO,
∴∠ABC′=∠ACO,
即∠BAN=∠ACO-∠OBD=∠DBC′,
由题意得DC′=1、DB= ,BC′=2 ,
∵S△DBC′= ,
∴DE= ,
∴BE= ,
∴tan∠DBC′=tan∠BAN= ,
设N(n,- n2+ n+2),且n>0,
∴tan∠BAN= = = ,
①当2n+2=9×(- n2+ n+2)时,n1= ,n2=-1(舍去);
②当2n+2=-9×(- n2+ n+2)时,n1= ,n2=-1(舍去);
∴N点的坐标为( , )或( ,- ).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十二章 二次函数单元测试 人教版数学 九年级上册
一、选择题(共8题,每题3分,满分24分)
1.如图,抛物线 与 轴只有一个公共点A(1,0),与 轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为( )
A.1 B.2 C.3 D.4
2.已知二次函数的图象(0≤x≤4)如图,关于该函数在所给自变量的取值范围内,下列说法正确的是( )
A.有最大值2,有最小值-2.5 B.有最大值2,有最小值1.5
C.有最大值1.5,有最小值-2.5 D.有最大值2,无最小值
3.已知关于x的不等式组 有解,则a的取值不可能是( )
A.0 B.1 C.2 D.-2
4.若点 在第二象限,则点 在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.函数y=﹣ax+a与y= (a≠0)在同一坐标系中的图象可能是( )
A. B.
C. D.
6.如图,正方形ABCD的边长为2,点O为其中心.将其绕点O顺时针旋转45°后得到正方形A'B'C'D',则旋转前后两正方形重叠部分构成的多边形的周长为( )(参考计算: )
A.16﹣8 B.16 ﹣16 C.12﹣8 D.16 ﹣12
7.已知二次函数y1=2x2-4x和一次函数y2=-2x,规定:当x任取一个值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较大值为M;若y1=y2,则M=y1=y2.下列说法错误的是( )
A.当x>2时,M=y1 B.当x<0时,M随x的增大而减小
C.M的最小值为-2 D.若M=-1时,则
8.二次函数的图象如图所示,有以下四个结论:①;②;③1和-3是关于的一元二次方程的两个实数根;④对于任意实数,都有.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(共5题,每题3分,满分15分)
9.如图,把抛物线y= x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为 .
10.关于x的方程﹣2x2+bx+c=0的解为x1、x2(x1<x2),﹣2x2+bx+c=1的解为x3、x4(x3<x4),用“<”连接x1、x2、x3、x4为 .
11.如图,已知二次函数y= x2﹣ x﹣3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为
12.如图正方形ABCD边长为2,E为CD边中点,P为射线BE上一点(P不与B重合),若△PDC为直角三角形,则BP= .
13.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为C(1,k),与y轴的交点在(0,2)、(0,3)之间(不包含端点),则k的取值范围是 .
三、解答题(共7题,满分81分)
14.如图,抛物线y= x2+mx+n与直线y=﹣ x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
(1)求抛物线的解析式和tan∠BAC的值;
(2)在(1)条件下,P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
15.如图1,已知二次函数y=x2+bx+c的图象与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为D,对称轴为直线l,
(1)求该二次函数的表达式;
(2)若点E是对称轴l右侧抛物线上一点,且S△ADE=2S△AOC,求点E的坐标;
(3)如图2,连接DC并延长交x轴于点F,设P为线段BF上一动点(不与B、F重合),过点P作PQ BD交直线BC于点Q,将直线PQ绕点P沿顺时针方向旋转45 后,所得的直线交DF于点R,连接OR.请直接写出当△PQR与△PFR相似时点P的坐标.
16.如图所示,已知抛物线经过点A(-2,0)、B(4,0)、C(0,-8),抛物线y=ax2+bx+c(a≠0)与直线y=x-4交于B,D两点.
(1)求抛物线的解析式并直接写出D点的坐标;
(2)点P为抛物线上的一个动点,且在直线BD下方,试求出△BDP面积的最大值及此时点P的坐标;
(3)点Q是线段BD上异于B、D的动点,过点Q作QF⊥x轴于点F,交抛物线于点G.当△QDG为直角三角形时,求点Q的坐标.
四、综合题
17.在直角坐标系xOy中,定义点C(a,b)为抛物线L:y=ax2+bx(a≠0)的特征点坐标.
(1)已知抛物线L经过点A(﹣2,﹣2)、B(﹣4,0),求出它的特征点坐标;
(2)若抛物线L1:y=ax2+bx的位置如图所示:
①抛物线L1:y=ax2+bx关于原点O对称的抛物线L2的解析式为 ;
②若抛物线L1的特征点C在抛物线L2的对称轴上,试求a、b之间的关系式;
③在②的条件下,已知抛物线L1、L2与x轴有两个不同的交点M、N,当一点C、M、N为顶点构成的三角形是等腰三角形时,求a的值.
18.如图,正方形 ,点 在边 上, 为等腰直角三角形.
(1)如图1,当 ,求证 ;
(2)如图2,当 ,取 的中点 ,连接 ,求证:
19.小明在学完了平行四边形后,想对“四边形的不稳定性”和“四边形的判定”有更好的理解,做了如下的探究:他用8根木棍和一些钉子组成了正方形和平行四边形(如图1),且,在同一条直线上,点落在边上.经小明测量,发现此时、、三个点在一条直线上,,.
(1)求的长.
(2)设的长度为,则 (用含的代数式表示).
(3)小明接着探究,在保证,位置不变的前提条件下,从点向右推动正方形,直到四边形刚好变为矩形时停止推动(如图2).若此时,求的长.
20.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c(a<0)经过点A(-1,0)、B(4,0)与y轴交于点C,tan∠ABC= .
(1)求抛物线的解析式;
(2)点M在第一象限的抛物线上,ME平行y轴交直线BC于点E,连接AC、CE,当ME取值最大值时,求△ACE的面积.
(3)在y轴负半轴上取点D(0,-1),连接BD,在抛物线上是否存在点N,使∠BAN=∠ACO-∠OBD?若存在,请求出点N的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】C
4.【答案】C
5.【答案】D
6.【答案】B
7.【答案】D
8.【答案】B
9.【答案】
10.【答案】x1<x3<x4<x2
11.【答案】(4,0)或(4, )
12.【答案】 或 或
13.【答案】 <k<4
14.【答案】解:(1)把A(0,3),C(3,0)代入y= x2+mx+n,得
,
解得: .
∴抛物线的解析式为y= x2﹣ x+3.
联立 ,
解得: 或 ,
∴点B的坐标为(4,1).
过点B作BH⊥x轴于H,如图1.∵C(3,0),B(4,1),
∴BH=1,OC=3,OH=4,CH=4﹣3=1,∴BH=CH=1.
∵∠BHC=90°,∴∠BCH=45°,BC= .
同理:∠ACO=45°,AC=3 ,
∴∠ACB=180°﹣45°﹣45°=90°,
∴tan∠BAC= ;
(2)存在点P,使得以A,P,Q为顶点的三角形与△ACB相似.
过点P作PG⊥y轴于G,
则∠PGA=90°.
设点P的横坐标为x,由P在y轴右侧可得x>0,则PG=x.
∵PQ⊥PA,∠ACB=90°,∴∠APQ=∠ACB=90°.
若点G在点A的下方,
①如图2①,当∠PAQ=∠CAB时,则△PAQ∽△CAB.
∵∠PGA=∠ACB=90°,∠PAQ=∠CAB,∴△PGA∽△BCA,
∴ .
∴AG=3PG=3x.
则P(x,3﹣3x).把P(x,3﹣3x)代入y= x2﹣ x+3,得: x2﹣ x+3=3﹣3x,
整理得:x2+x=0,解得:x1=0(舍去),x2=﹣1(舍去).
②如图2②,
当∠PAQ=∠CBA时,则△PAQ∽△CBA.
同理可得:AG= PG= x,则P(x,3﹣ x),
把P(x,3﹣ x)代入y= x2﹣ x+3,得: x2﹣ x+3=3﹣ x,
整理得:x2﹣ x=0,解得:x1=0(舍去),x2= ,∴P( , );
若点G在点A的上方,
①当∠PAQ=∠CAB时,则△PAQ∽△CAB,
同理可得:点P的坐标为(11,36).
②当∠PAQ=∠CBA时,则△PAQ∽△CBA.
同理可得:点P的坐标为P( , ).
综上所述:满足条件的点P的坐标为(11,36)、( , )、( , ).
15.【答案】(1)解:将A(-1,0)、B(3,0)代入二次函数y=x2+bx+c,得
解得
则二次函数为y=x2-2x-3.
(2)解:设E(m,m2–2m–3),过点E作EM//x轴,交AD于点M,
由二次函数为y=x2-2x-3,可得C(0,-3),D(1,-4),
则S△ADE=S△AOC=2× ×3×1=3.
∵A(–1,0)、D(1,–4)
∴直线AD为:y=–2x–2,
∵E(m,m2–2m–3),
∴M( m2+m+ ,m2–2m–3),
∴EM= m-( m2+m+ )= m2 ,
∴S△ADE= ×4EM=2EM= m2-1=3,
解得m=±2(其中m =–2舍去),
∴E(2–3).
(3)解:由B(3,0)和C(0,-3)可得直线BC为y=x-3,
由B(3,0)和D(1,-4)可得直线BD为y=2x-6,
设P(n,0),因为PQ//BD,则可设PQ为y=2(x-n),
联立
解得
则Q(2n-3,2n-6),
由C(0,-3)和D(1,-4)可得直线CD为y=-x-3,则F(-3,0),
所以OF=OC,则∠OFR=45°,
则∠RPQ=∠OFR=45°.
当△QPR与△PFR时,有△RPQ~△PFR和△QPR~△PFR两种情况:
①当△RPQ~△PFR时,∠QRP=∠RPF,则RQ//x轴,则点R的纵坐标与点Q相等,
当y=2n-6代入直线CD可解得x=-2n+3,R(-2n+3,2n-6),
即RQ=2n-3-(-2n+3)=4n-6,RP2= ,
又PF=3+n,因为 ,
所以RP2=PF·RQ,
即 =(3+n)(4n-6),
化简得9n2-48n+63=0,
即(3n-7)(3n-9)=0,
解得n= 或n=3(舍去);
当n= 时,P1( ,0);
②当△QPR~△PFR时,∠PRQ=∠FRP,P2(0,0).
综上,P1( ),P2(0,0).
16.【答案】(1)设抛物线的解析式为y=ax2+bx+c∵抛物线经过点A(-2,0)、B(4,0)、C(0,-8)∴,解得.
∴抛物线的解析式为y=x2-2x-8
点D的坐标为(-1,-5)
(2)过P作PE∥y轴,交直线AB于点E
设P(x,x2-2x-8)则E(x,x-4)
∴PE=x-4-(x2-2x-8)=-x2+3x+4
∴S△BDP=S△DEP+S△BEP= PE·(xE-xD)+ PE·(xB-xE)
= PE·(xB-xD)= PE= (-x2+3x+4)
=- (x- )2+
∴当x= 时,△BDP面积的最大值为
此时点P的坐标为( ,- )
(3)设直线y=x-4与y轴相交于点K,则K(0,-4)∵B(4,0),∴OB=OK=4,∴∠OKB=∠OBK=45°
∵QF⊥x轴,∴∠DQG=45°
若△QDG为直角三角形,则△QDG是等腰直角三角形①∠QDG=90°,过D作DH⊥QG于H,∴QG=2DH,
∴-x2+3x+4=2(x+1),解得x 1=-1(舍去),
x 2=2,∴Q1(2,-2)
②∠DGQ=90°,则DH=QH,∴-x2+3x+4=x+1,解得x 1=-1(舍去),x 2=3,∴P2(3,-1)综上所述,当△QDG为直角三角形时,点Q的坐标为(2,-2)或(3,-1)
17.【答案】(1)解:将点A(﹣2,﹣2)、B(﹣4,0)代入到抛物线解析式中,得
,解得: .∴抛物线L的解析式为 ,
∴它的特征点为( ,2).
(2)y=﹣ax2+bx;解:②∵抛物线L2的对称轴为直线:x= .∴当抛物线L1的特征点C(a,b)在抛物线L2的对称轴上时,有a= ,∴a与b的关系式为b=2a2. ③∵抛物线L1、L2与x轴有两个不同的交点M、N,∴在抛物线L1:y=ax2+bx中,令y=0,即ax2+bx=0,解得:x1= ,x2=0(舍去),即点M( ,0);在抛物线L2:y=﹣ax2+bx中,令y=0,即﹣ax2+bx=0,解得:x1= ,x2=0(舍去),即点N( ,0).∵b=2a2,∴点M(﹣2a,0),点N(2a,0),点C(a,2a2).∴MN=2a﹣(﹣2a)=4a,MC= ,NC= .因此以点C、M、N为顶点的三角形是等腰三角形时,有以下三种可能:(1)MC=MN,此时有: =4a,即9a2+4a4=16a2,解得:a=0,或a= ,∵a<0,∴a= ;(2)NC=MN,此时有: =4a,即a2+4a4=16a2,解得:a=0,或a= ,∵a<0,∴a= ;(3)MC=NC,此时有: = ,即9a2=a2,解得:a=0,又∵a<0,∴此情况不存在.综上所述:当以点C、M、N为顶点的三角形是等腰三角形时,a的值为 或 .
18.【答案】(1)证明:作 ,
四边形 是正方形
是等腰直角三角形
(2)连接 ,在 上截取 ,使得 ,连接 ,
为等腰直角三角形,
四边形 是正方形
三点共线
为 的中点,
在 中,
即
19.【答案】(1)解:∵四边形是平行四边形,
∴,,
∴.
∵四边形是正方形,
∴,,
∴,
∴,
∴,
∴,
∴,
∴
(2)
(3)解:∵在推动过程中,位置不变,的长度保持不变,
∴设,则.
∵四边形是矩形,
∴,,
∴,
∴.
∴,
∵,解得,
,,
∴.
20.【答案】(1)解:∵B(4,0),
∴OB=4,
∵tan∠ABC= = = ,
∴OC=2,
∴C(0,2),
设y=a(x-1)(x-4),
把C(0,2)代入,得a=- ,
∴抛物线的解析式为y=- (x-1)(x-4)=- x2+ x+2;
(2)解:设直线BC的解析式为y=kx+2,
把B(4,0)代入,得k=- ,
∴直线BC解析式为y=- x+2,
设M(m,- m2+ m+2),
则E(m,- m+2),
∴ME=- m2+2m,
∴当m=2时,ME取得最大值2,
∴E(2,1),
∴S△ACE=S△ABC-S△ABE= ×5×(2-1)= ;
(3)解:作C′(0,-2)与 C关于x轴对称,连接BC′,过点D作DE⊥BC′于点E,
∴∠ABC=∠ABC′,
∵ = ,∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴∠ABC=∠ACO,
∴∠ABC′=∠ACO,
即∠BAN=∠ACO-∠OBD=∠DBC′,
由题意得DC′=1、DB= ,BC′=2 ,
∵S△DBC′= ,
∴DE= ,
∴BE= ,
∴tan∠DBC′=tan∠BAN= ,
设N(n,- n2+ n+2),且n>0,
∴tan∠BAN= = = ,
①当2n+2=9×(- n2+ n+2)时,n1= ,n2=-1(舍去);
②当2n+2=-9×(- n2+ n+2)时,n1= ,n2=-1(舍去);
∴N点的坐标为( , )或( ,- ).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
