2.6应用一元二次方程 课件(21张PPT)
文档属性
| 名称 | 2.6应用一元二次方程 课件(21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 09:26:47 | ||
图片预览







文档简介
(共21张PPT)
第二章 一元二次方程
第6节 应用一元二次方程
1.掌握列一元二次方程解决几何问题、数学问题,并能根据具体 问题的实际意义,检验结果的合理性.(重点、难点)
2.理解将实际问题抽象为方程模型的过程,并能运用所学的知识解决问题.
想一想:通过前面的学习你知道解一元二次方程有哪些方法吗?
配方法(直接开平方法)、公式法、因式分解法
列一元一次方程解应用题分几步呢?应注意哪些?
①审题
②设出未知数
③找等量关系
④列方程
⑤解方程
⑥作答
你还记得本章开始时梯子下滑的问题吗?
如图,一个长为 10 m 的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为 8 m.如果梯子的顶端下滑 1 m,那么梯子的底端滑动多少米?
一元二次方程解决几何问题
1—
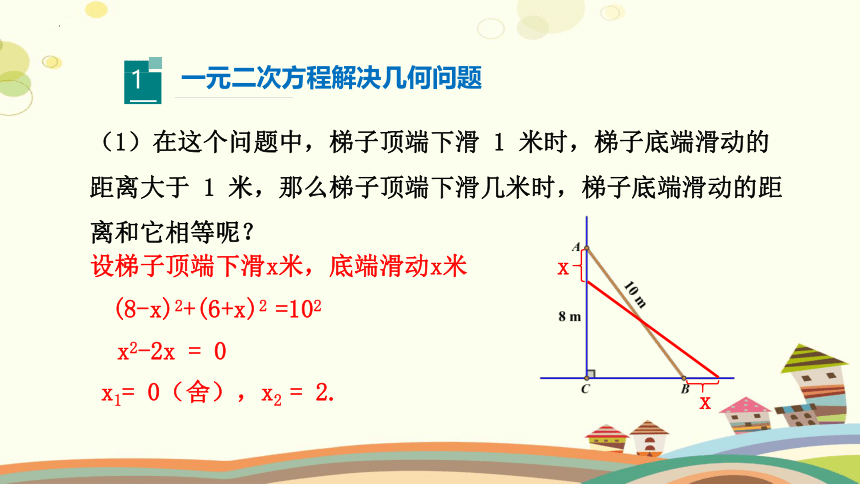
(1)在这个问题中,梯子顶端下滑 1 米时,梯子底端滑动的距离大于 1 米,那么梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?
x
x
设梯子顶端下滑x米,底端滑动x米
(8-x)2+(6+x)2 =102
x2-2x = 0
x1= 0(舍),x2 = 2.
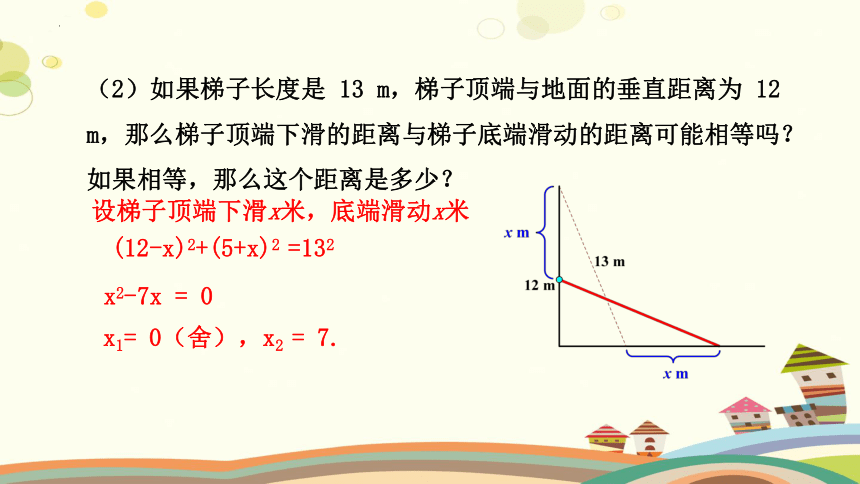
(2)如果梯子长度是 13 m,梯子顶端与地面的垂直距离为 12 m,那么梯子顶端下滑的距离与梯子底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
设梯子顶端下滑x米,底端滑动x米
(12-x)2+(5+x)2 =132
x2-7x = 0
x1= 0(舍),x2 = 7.
例1.如图,某海军基地位于A处,在其正南方向200n mile 处有一目标B,在B的正东方向200n mile处有一重要目标C.
小岛D位于AC的中点,岛上有一补给码头;小岛F位于
BC的中点.一艘军舰沿A出发,经B到C匀速巡航,一艘
补给船同时从D出发,沿南偏西方向匀速直线航行,
欲将一批物品送达军舰.
北
东
A
B
C
(1)小岛D与小岛F相距多少海里
东
北
A
B
C
D
F
解:连接DF.∵AD=CD , BF=CF,
∴DF是△ABC的中位线.
∴DF∥AB,且DF= AB,
∵AB⊥BC, AB = BC =200n mile,
∴DF⊥BC, DF =100n mile.
已知军舰的速度是补给船的 2 倍,军舰在由 B 到 C 的途中与补给船相遇,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)
东
北
A
B
C
D
F
E
解: 设相遇是补给船航行了x n mile,那么
DE = x n mile , AE + BE = 2x n mile,
EF=AB +BF-(AB + BE) =(300 - 2x)n mile.
在Rt△DEF中,根据勾股定理可得方程
x2 = 1002 + (300 - 2x)2.
整理得: 3x2 - 1200x + 100000 = 0 ,
解方程得 (舍去)
例2.一块长和宽分别为60 cm 和40 cm 的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体,使它的底面积为800 cm2. 求截去正方形的边长.
800cm2
x
x
解:设截取正方形的边长为xm. 根据题意,得
(60 - 2x)(40 - 2x) = 800.
整理,得 x2 - 50x + 400 = 0.
解方程,得x1=10 ,x2= 40 (不合题意,舍去).
答:截去正方形的边长为10 cm.
(60 - 2x)
(40-2x)
例3.新华商场销售某种冰箱,每台进货价为 2500 元。市场调研表明:当销售价为 2900 元时,平均每天能售出 8 台;而当销售价每降低 50 元时,平均每天就能多售出 4 台。商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的降价应为多少元?
分析基本数量关系
售价 - 进价 = 利润
每台利润 × 每天的销售量 = 每天的总利润
例3.新华商场销售某种冰箱,每台进货价为 2500 元。市场调研表明:当销售价为 2900 元时,平均每天能售出 8 台;而当销售价每降低 50 元时,平均每天就能多售出 4 台。商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的降价应为多少元?
进价 售价 销售量 每台利润 总利润
降价前
降价后
2500
2900
8
400
400×8
2500
未知
未知
未知
5000
设每台冰箱降价 x 元
售价每降低 50 元
多售出 4 台
售价每降低 100 元
多售出 4× 台
售价每降低 x 元
多售出 4× 台
例3.新华商场销售某种冰箱,每台进货价为 2500 元。市场调研表明:当销售价为 2900 元时,平均每天能售出 8 台;而当销售价每降低 50 元时,平均每天就能多售出 4 台。商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的降价应为多少元?
解:设每台冰箱降价 x 元,根据题意,得
8+4×
( 2900-x -2500)( ) = 5000
解这个方程,得
x1 = x2 = 150.
2900-150 = 2750
所以,每台冰箱应定价为 2750 元.
某商场将进货价为 30 元的台灯以 40 元售出,平均每月能售出 600 个。调查发现:售价在 40 元至 60 元范围内,这种台灯的售价每上涨 1 元,其销售量就将减少 10 个.为了实现平均每月 10 000 元的销售利润,这种台灯的售价应定为多少?这时应购进台灯多少个?
解:设这种台灯售价上涨 x 元,根据题意,得
(40+x-30)(600-10x) = 10 000
解这个方程,得
x1 = 10.
x2 = 40(舍).
售价为:40+x = 40+10 = 50(元)
应购置台灯:600-10x = 600-10×10 = 500(个)
列方程解应用题的一般步骤:
审:审清题意:已知什么?求什么?已知、未知之间有什么关系?
设:设未知数,语句要完整;(可以直接设:问什么设什么;也可以间接设.)
列:列代数式表示题中的量,找等量关系,根据等量关系列方程;
解:解所列的方程;
验:检验是否是所列方程的根;是否符合题意;
答:答案也必须是完整的语句.
归纳总结
例4.某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株
整理,得 x2 - 3x + 2 = 0.
解这个方程,得 x1=1, x2=2.
经检验,x1=1 , x2 = 2 都符合题意.
答:要使每盆的盈利达到10元,每盆应植入4株或5株.
解:设每盆花苗增加的株数为x株,则每盆花苗有(x+3)株,平均单株盈利为(3 - 0.5x)元.根据题意,得
(x + 3)(3 - 0.5x) = 10.
1.某公司去年的各项经营中,一月份的营业额为200万,一月、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率.
2.生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了182件,如果全组有x名同学,那么根据题意列出的方程是( )
A. x(x+1)=182 B. x(x-1)=182
C. 2x(x+1)=182 D. x(1-x)=182×2
3.某种服装,平均每天可销售 20 件,每件赢利 44 元. 在每件降价幅度不超过 10 元的情况下,若每件降价 1 元,则每天可多售 5 件.如果每天要赢利 1600 元,每件应降价多少元?
学习了这节课你有哪些收获?
第二章 一元二次方程
第6节 应用一元二次方程
1.掌握列一元二次方程解决几何问题、数学问题,并能根据具体 问题的实际意义,检验结果的合理性.(重点、难点)
2.理解将实际问题抽象为方程模型的过程,并能运用所学的知识解决问题.
想一想:通过前面的学习你知道解一元二次方程有哪些方法吗?
配方法(直接开平方法)、公式法、因式分解法
列一元一次方程解应用题分几步呢?应注意哪些?
①审题
②设出未知数
③找等量关系
④列方程
⑤解方程
⑥作答
你还记得本章开始时梯子下滑的问题吗?
如图,一个长为 10 m 的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为 8 m.如果梯子的顶端下滑 1 m,那么梯子的底端滑动多少米?
一元二次方程解决几何问题
1—
(1)在这个问题中,梯子顶端下滑 1 米时,梯子底端滑动的距离大于 1 米,那么梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?
x
x
设梯子顶端下滑x米,底端滑动x米
(8-x)2+(6+x)2 =102
x2-2x = 0
x1= 0(舍),x2 = 2.
(2)如果梯子长度是 13 m,梯子顶端与地面的垂直距离为 12 m,那么梯子顶端下滑的距离与梯子底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
设梯子顶端下滑x米,底端滑动x米
(12-x)2+(5+x)2 =132
x2-7x = 0
x1= 0(舍),x2 = 7.
例1.如图,某海军基地位于A处,在其正南方向200n mile 处有一目标B,在B的正东方向200n mile处有一重要目标C.
小岛D位于AC的中点,岛上有一补给码头;小岛F位于
BC的中点.一艘军舰沿A出发,经B到C匀速巡航,一艘
补给船同时从D出发,沿南偏西方向匀速直线航行,
欲将一批物品送达军舰.
北
东
A
B
C
(1)小岛D与小岛F相距多少海里
东
北
A
B
C
D
F
解:连接DF.∵AD=CD , BF=CF,
∴DF是△ABC的中位线.
∴DF∥AB,且DF= AB,
∵AB⊥BC, AB = BC =200n mile,
∴DF⊥BC, DF =100n mile.
已知军舰的速度是补给船的 2 倍,军舰在由 B 到 C 的途中与补给船相遇,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)
东
北
A
B
C
D
F
E
解: 设相遇是补给船航行了x n mile,那么
DE = x n mile , AE + BE = 2x n mile,
EF=AB +BF-(AB + BE) =(300 - 2x)n mile.
在Rt△DEF中,根据勾股定理可得方程
x2 = 1002 + (300 - 2x)2.
整理得: 3x2 - 1200x + 100000 = 0 ,
解方程得 (舍去)
例2.一块长和宽分别为60 cm 和40 cm 的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体,使它的底面积为800 cm2. 求截去正方形的边长.
800cm2
x
x
解:设截取正方形的边长为xm. 根据题意,得
(60 - 2x)(40 - 2x) = 800.
整理,得 x2 - 50x + 400 = 0.
解方程,得x1=10 ,x2= 40 (不合题意,舍去).
答:截去正方形的边长为10 cm.
(60 - 2x)
(40-2x)
例3.新华商场销售某种冰箱,每台进货价为 2500 元。市场调研表明:当销售价为 2900 元时,平均每天能售出 8 台;而当销售价每降低 50 元时,平均每天就能多售出 4 台。商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的降价应为多少元?
分析基本数量关系
售价 - 进价 = 利润
每台利润 × 每天的销售量 = 每天的总利润
例3.新华商场销售某种冰箱,每台进货价为 2500 元。市场调研表明:当销售价为 2900 元时,平均每天能售出 8 台;而当销售价每降低 50 元时,平均每天就能多售出 4 台。商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的降价应为多少元?
进价 售价 销售量 每台利润 总利润
降价前
降价后
2500
2900
8
400
400×8
2500
未知
未知
未知
5000
设每台冰箱降价 x 元
售价每降低 50 元
多售出 4 台
售价每降低 100 元
多售出 4× 台
售价每降低 x 元
多售出 4× 台
例3.新华商场销售某种冰箱,每台进货价为 2500 元。市场调研表明:当销售价为 2900 元时,平均每天能售出 8 台;而当销售价每降低 50 元时,平均每天就能多售出 4 台。商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的降价应为多少元?
解:设每台冰箱降价 x 元,根据题意,得
8+4×
( 2900-x -2500)( ) = 5000
解这个方程,得
x1 = x2 = 150.
2900-150 = 2750
所以,每台冰箱应定价为 2750 元.
某商场将进货价为 30 元的台灯以 40 元售出,平均每月能售出 600 个。调查发现:售价在 40 元至 60 元范围内,这种台灯的售价每上涨 1 元,其销售量就将减少 10 个.为了实现平均每月 10 000 元的销售利润,这种台灯的售价应定为多少?这时应购进台灯多少个?
解:设这种台灯售价上涨 x 元,根据题意,得
(40+x-30)(600-10x) = 10 000
解这个方程,得
x1 = 10.
x2 = 40(舍).
售价为:40+x = 40+10 = 50(元)
应购置台灯:600-10x = 600-10×10 = 500(个)
列方程解应用题的一般步骤:
审:审清题意:已知什么?求什么?已知、未知之间有什么关系?
设:设未知数,语句要完整;(可以直接设:问什么设什么;也可以间接设.)
列:列代数式表示题中的量,找等量关系,根据等量关系列方程;
解:解所列的方程;
验:检验是否是所列方程的根;是否符合题意;
答:答案也必须是完整的语句.
归纳总结
例4.某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株
整理,得 x2 - 3x + 2 = 0.
解这个方程,得 x1=1, x2=2.
经检验,x1=1 , x2 = 2 都符合题意.
答:要使每盆的盈利达到10元,每盆应植入4株或5株.
解:设每盆花苗增加的株数为x株,则每盆花苗有(x+3)株,平均单株盈利为(3 - 0.5x)元.根据题意,得
(x + 3)(3 - 0.5x) = 10.
1.某公司去年的各项经营中,一月份的营业额为200万,一月、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率.
2.生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了182件,如果全组有x名同学,那么根据题意列出的方程是( )
A. x(x+1)=182 B. x(x-1)=182
C. 2x(x+1)=182 D. x(1-x)=182×2
3.某种服装,平均每天可销售 20 件,每件赢利 44 元. 在每件降价幅度不超过 10 元的情况下,若每件降价 1 元,则每天可多售 5 件.如果每天要赢利 1600 元,每件应降价多少元?
学习了这节课你有哪些收获?
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
