人教版高中数学必修第二册9.2.1 总体取值规律的估计-9.2.2总体百分位数的估计 同步精练(含解析)
文档属性
| 名称 | 人教版高中数学必修第二册9.2.1 总体取值规律的估计-9.2.2总体百分位数的估计 同步精练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-19 11:46:00 | ||
图片预览




文档简介
人教版高中数学必修第二册
9.2.1 总体取值规律的估计-9.2.2总体百分位数的估计 同步精练
【考点梳理】
考点一:频率分布直方图
作频率分布直方图的步骤
1.求极差:极差为一组数据中最大值与最小值的差.
2.决定组距与组数
将数据分组时,一般取等长组距,并且组距应力求“取整”,组数应力求合适,以使数据的分布规律能较清楚地呈现出来.
3.将数据分组
4.列频率分布表
各小组的频率=.
5.画频率分布直方图
纵轴表示,实际上就是频率分布直方图中各小长方形的高度,小长方形的面积=组距×=频率.
技巧归纳:
(1)分点的决定方法:若数据为整数,则减去0.5作为分点数;若数据是小数点后一位的数,则减去0.05作为分点数;依次类推.
(2)画频率分布直方图中小矩形的高的方法:①小矩形的高=;②假设频数为1的小矩形的高为h,则频数为k的小矩形的高为kh.
(3)频率分布直方图的性质
①因为小矩形的面积=组距×=频率,所以各小矩形的面积表示相应各组的频率.这样,频率分布直方图就以面积的形式反映了数据落在各个小组内的频率大小.
②在频率分布直方图中,各小矩形的面积之和等于1.
③=样本容量.
(2)频率分布直方图反映了样本在各个范围内取值的可能性,由抽样的代表性利用样本在某一范围内的频率,可近似地估计总体在这一范围内的可能性.
考点二:常见统计图表的特点与区别
扇形图主要用于直观描述各类数据占总数的比例,条形图和直方图主要用于直观描述不同类别或分组数据的频数和频率,条形图适用于描述离散型数据,直方图适用于描述连续型数据.折线图主要用于描述数据随时间的变化趋势.
考点三:百分位数
1.百分位数定义:一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
2.常用的百分位数
(1)四分位数:第25百分位数,第50百分位数,第75百分位数.
(2)其它常用的百分位数:第1百分位数,第5百分位数,第95百分位数,第99百分位数.
3.计算一组n个数据的第p百分位数的一般步骤如下:
第1步,按从小到大排列原始数据;
第2步,计算i=n×p%;
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
【题型归纳】
题型一:频率分布概念的理解
1.(2021·全国·高一专题练习)某超市计划按月订购一种冷饮,根据往年销售经验,每天需求量与当天最高气温(单位:)有关.如果最高气温不低于,需求量为瓶;如果最高气温位于区间(单位:)内,需求量为瓶;如果最高气温低于,需求量为瓶.为了确定月份的订购计划,统计了前三年月份各天的最高气温数据,得到下面的频数分布表:
最高气温
天数
将最高气温位于各区间的频率视为最高气温位于该区间的概率,若月份这种冷饮一天的需求量不超过瓶的概率估计值为,则( )
A. B. C. D.
2.(2020·江苏·海安高级中学高一期中)一个班数学成绩频率分布表(样本容量为)不小心损坏了一部分,只记得样本中数据在上的频率为,则估计样本在、内的数据个数共有( )
分组
频数
A.28 B.30 C.32 D.34
3.(2020·天津河西·高一期中)在“世界杯”足球赛闭幕后,某中学学生会对本校高一年级1000名学生收看比赛的情况用随机抽样方式进行调查,样本容量为50,将数据分组整理后,列表如表:
观看场数 0 1 2 3 4 5 6 7
观看人数占调查人数的百分比 8% 10% 20% 26% m% 12% 6% 2%
从表中可以得出正确的结论为( )
A.表中m的数值为8 B.估计观看比赛不低于4场的学生约为360人
C.估计观看比赛不低于4场的学生约为720人 D.估计观看比赛场数的众数为2
题型二:画频率分布直方图
4.(2022·湖南·高一)下面是北方某城市2018年1—2月的日平均气温(单位:℃)的记录数据:
2 7 8 9
0 5
0 5
2 7 5
(1)将数据适当分组,并画出相应的频率分布直方图;
(2)试估计该城市1—2月的日平均气温在0℃以下的天数所占的百分比.
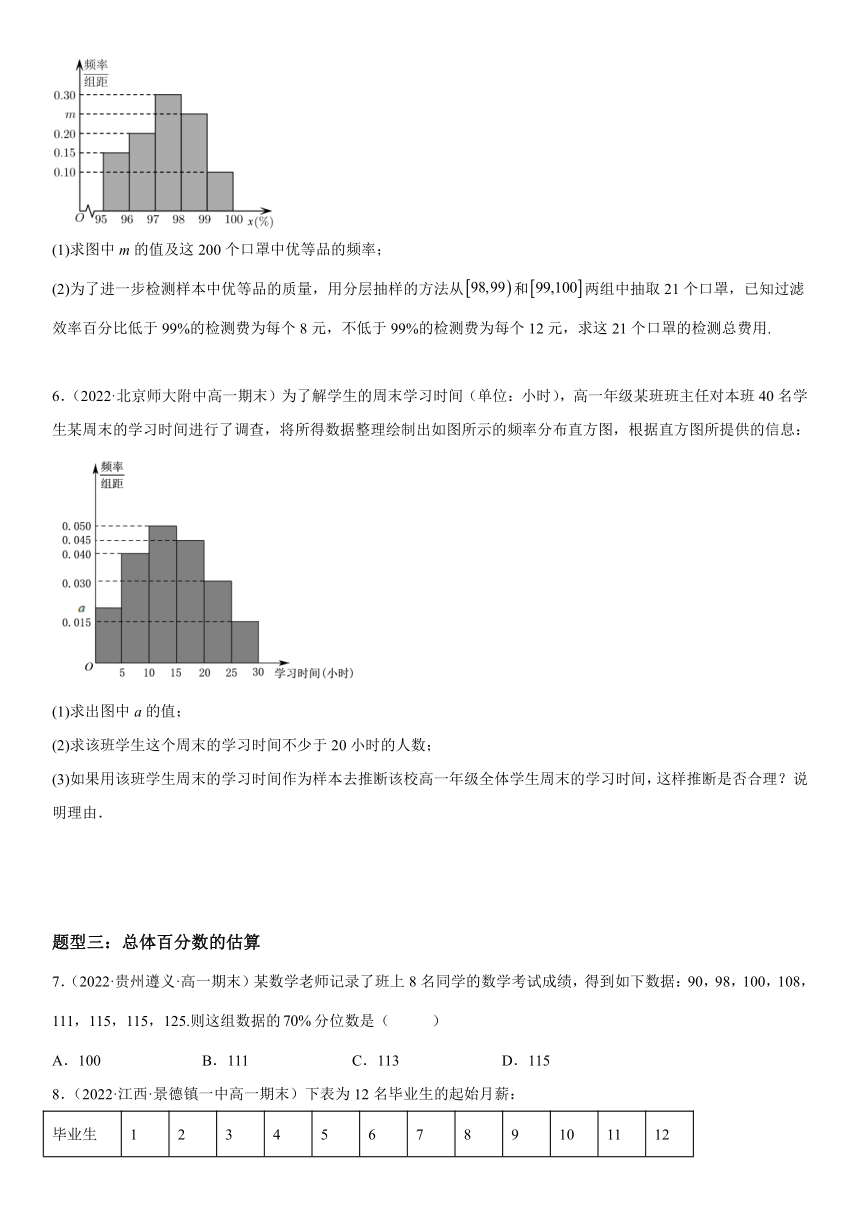
5.(2022·辽宁朝阳·高一)一次性医用口罩是适用于覆盖使用者的口 鼻及下颌,用于普通医疗环境中阻隔口腔和鼻腔呼出或喷出污染物的一次性口罩.按照我国医药行业标准,口罩对细菌的过滤效率达到95%及以上为合格,98%及以上为优等品.某部门为了检测一批口罩对细菌的过滤效率,随机抽检了200个口罩,将它们的过滤效率(百分比)按照,,,,分成5组,制成如图所示的频率分布直方图.
(1)求图中m的值及这200个口罩中优等品的频率;
(2)为了进一步检测样本中优等品的质量,用分层抽样的方法从和两组中抽取21个口罩,已知过滤效率百分比低于99%的检测费为每个8元,不低于99%的检测费为每个12元,求这21个口罩的检测总费用.
6.(2022·北京师大附中高一期末)为了解学生的周末学习时间(单位:小时),高一年级某班班主任对本班40名学生某周末的学习时间进行了调查,将所得数据整理绘制出如图所示的频率分布直方图,根据直方图所提供的信息:
(1)求出图中a的值;
(2)求该班学生这个周末的学习时间不少于20小时的人数;
(3)如果用该班学生周末的学习时间作为样本去推断该校高一年级全体学生周末的学习时间,这样推断是否合理?说明理由.
题型三:总体百分数的估算
7.(2022·贵州遵义·高一期末)某数学老师记录了班上8名同学的数学考试成绩,得到如下数据:90,98,100,108,111,115,115,125.则这组数据的分位数是( )
A.100 B.111 C.113 D.115
8.(2022·江西·景德镇一中高一期末)下表为12名毕业生的起始月薪:
毕业生 1 2 3 4 5 6 7 8 9 10 11 12
起始月薪 2850 2950 3050 2880 2755 2710 2890 3130 2940 3325 2920 2880
根据表中所给的数据计算75%分位数为( )
A.2950 B.3050 C.3130 D.3000
9.(2022·辽宁丹东·高一期末)某地区想实行阶梯电价,经调查发现,该地区居民用电量信息如下:
分位数 50%分位数 70%分位数 80%分位数 90%分位数
用电量 160 176 215 230
如果要求约70%的居民用电在第一阶梯内,约20%的居民用电在第二阶梯内,可确定第二阶梯电价的用电量范围为( )
A. B. C. D.
题型四:频率分布直方图的性质
10.(2022·天津河北·一模)某高校调查了400名学生每周的自习时间(单位:小时),绘制成如图所示的频率分布直方图,其中自习时间的范围是,样本数据分组为,,,,.则根据直方图这400名学生中每周的自习时间不足22.5小时的人数是( )
A.60 B.90 C.130 D.150
11.(2022·陕西·武功县普集高级中学高一阶段练习)为了研究人们生活健康情况,某市随机选取年龄在15~75岁之间的1000人进行调查,得到频率分布直方图如图所示,其中,利用分层抽样从年龄在,,,,,之间共选取20名市民书写生活健康的报告,其中选取年龄在市民的人数为( )
A.2 B.3 C.4 D.7
12.(2021·全国·高一课时练习)根据《中华人民共和国道路交通安全法》规定:血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车,处十五日以下拘留和三个月以上六个月以下暂扣驾驶证,并处500元以上2000元以下罚款.据《法制晚报》报道,2009年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共500人.如图,这是对这500人酒后驾车血液中酒精含量进行检测所得结果的频率直方图,则属于醉酒驾车的人数约为( )
A.25 B.50 C.75 D.100
【双基达标】
一、单选题
13.(2022·陕西·西安市阎良区关山中学高一阶段练习)在一次高二数学单元评估中,共有500名同学参加调研测试,经过评估,这500名学生的得分都在之间,其得分的频率分布直方图如图,则得分在之间的学生人数是( )
A.150 B.200 C.250 D.300
14.(2022·陕西·武功县普集高级中学高一阶段练习)为保障食品安全,某监管部门对辖区内一家食品企业进行检查,现从其生产的某种产品中随机抽取100件作为样本,并以产品的一项关键质量指标值为检测依据,整理得到如下的样本频率分布直方图.若质量指标值在内的产品为一等品,则该企业生产的产品为一等品的概率约为( )
A.0.38 B.0.61
C.0.122 D.0.75
15.(2021·江西上饶·高一阶段练习)采用简单随机抽样抽到一个容量为20的样本数据,分组后,各组的频数如下表:
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70)
频数 2 3 x 5 y 2
已知样本数据在区间[20,40)内的频率为0.35,则样本数据在区间[50,60)内的频率为( )
A.0.70 B.0.50 C.0.25 D.0.20
16.(2021·全国·高一单元测试)一个容量为的样本,其数据的分组与各组的频数如下:
分组
频数
则样本数据落在内的频率为( )
A. B. C. D.
17.(2021·甘肃·嘉峪关市第一中学高一期中)在高一(1)班组织的“我爱古诗词”的调研考试中,全班40名学生的成绩数据(均为整数且都在)统计为如下的频率分布直方图,则第四小组(成绩分布在)的频率为( )
A.0.001 B.0.01 C.0.03 D.0.3
18.(2021·陕西铜川·高一期中)某校将举办秋季体育文化节,为了解该校学生的身体状况,抽取部分男生和女生的体重,将男生体重数据整理后,作出了频率分布直方图,已知图中从左到右前三个小组频率之比为,第二小组频数为13,若全校男、女生比例为,则全校抽取的学生人数为( )
A.100 B.80 C.45 D.32
19.(2021·陕西渭南·高一期末)抽样统计某校部分学生的物理测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是( )
A. B.
C. D.
20.(2021·全国·高一课时练习)某个高级中学组织物理 化学学科能力竞赛,全校1000名学生都参加两科考试,考试后按学科分别评出一 二 三等奖和淘汰的这四个等级,现有某考场的两科考试数据统计如下,其中物理科目成绩为二等奖的考生有12人.如果以这个考场考生的物理和化学成绩去估计全校考生的物理和化学成绩分布,则以下说法正确的是( )
①该考场化学考试获得一等奖的有4人;
②全校物理考试获得二等奖的有240人;
③如果采用分层抽样从全校抽取200人,则化学考试被淘汰78人.
A.①②③ B.②③ C.①② D.①③
21.(2021·陕西铜川·高一期末)某班50名学生在一次百米测试中,成绩全部不小于13秒且小于19秒,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…;第六组,成绩大于等于18秒且小于19秒,如图是按上述分组方法得到的频率分布直方图,设成绩小于17秒的学生人数占全班总人数的百分比为,成绩大于等于15秒且小于17秒的学生人数为,则从频率分布直方图中可分析出和的值分别是( )
A.,35 B.,45
C.,35 D.,45
【高分突破】
一:单选题
22.(2021·黑龙江·大庆市东风中学高一期末)在样本的频率分布直方图中,共有5个小长方形,若中间一个长方形的面积等于其他4个小长方形面积和的,且样本容量为210,则中间一组的频数为( )
A.10 B.20 C.60 D.70
23.(2022·河南南阳·高一期末)体育老师记录了班上10名同学1分钟内的跳绳次数,得到如下数据:88,94,96,98,98,99,100,101,101,116.这组数据的60%分位数是( )
A.98 B.99 C.99.5 D.100
24.(2021·辽宁·高一期末)从800件产品中抽取6件进行质检,利用随机数表法抽取样本时,先将800件产品按001,002,…,800进行编号.如果从随机数表第8行第8列的数8开始往右读数(随机数表第7行至第9行的数如下),则抽取的6件产品的编号的75%分位数是( )
……
8442175331 5724550688 77047447672176335025 8392120676
6301637859 1695566711 69105671751286735807 4439523879
3321123429 7864560782 52420744381551001342 9966027954
A.105 B.556 C.671 D.169
25.(2022·全国·高一课时练习)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是,样本数据分组为,,,,.根据频率分布直方图,估计这200名学生每周的自习时间数据的第30百分位数为( )
A.22 B.21.25 C.22.5 D.25
26.(2021·河北·衡水市冀州区第一中学高一期末)幸福指数是某个人主观地评价他对自己目前生活状态的满意程度指标,常用内的一个数来表示,该数越接近10表示满意程度越高.现随机抽取8位小区居民,他们的幸福指数分别是3,4,5,6,7,8,9,5,则这组数据的第70百分位数是( )
A.6 B.7 C.7.5 D.8
27.(2021·全国·高一课前预习)甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则( )
A.甲的成绩的平均数小于乙的成绩的平均数
B.甲的成绩的中位数等于乙的成绩的中位数
C.甲的成绩的第80百分位数等于乙的成绩的第80百分位数
D.甲的成绩的极差大于乙的成绩的极差
28.(2021·全国·高一课前预习)某校组织全体学生参加了主题为“建党百年,薪火相传”的知识竞赛,随机抽取了200名学生进行成绩统计,发现抽取的学生的成绩都在50分至100分之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示,下列说法正确的是( )
A.直方图中的值为0.004
B.在被抽取的学生中,成绩在区间[70,80)的学生数为15人
C.估计全校学生成绩的样本数据的80%分位数约为93分
D.估计全校学生的平均成绩为84分
29.(2022·全国·高一专题练习)通过抽样调查得到某栋居民楼24户居民的月均用水量数量(单位:),将其按从小到大排序如下:
2.1 3.2 3.2 4.3 4.3 5.5 6.7 8.9 9.4 9.5 9.5 9.9
10.1 10.5 11.1 11.2 12.5 14.8 15.2 15.3 18.4 19.0 20.8 22.4
则估计这24户居民的月均用水量的第25百分位数为( )
A.4.3 B.5.5 C.6.1 D.6.7
30.(2021·广东佛山·高一期末)棉花的纤维长度是棉花质量的重要指标,在一批棉花中随机抽到了60根棉花的纤维长度(单位:mm),按从小到大排序结果如下:
25 28 33 50 52 58 59 60 61 62 82 86 113 115 140 143 146 170 175 195 202 206 233 236 238 255 260 263 264 265 293 293 294 296 301 302 303 305 305 306 321 323 325 326 328 340 343 346 348 350 352 355 357 357 358 360 370 380 383 385.
请你估算这批棉花的第75百分位数是( )
A.334 B.327 C.328 D.329
二、多选题
31.(2022·安徽蚌埠·高一期末)某市为了考察一所高中全体学生参与第六届全国中小学生“学宪法、讲宪法”宪法小卫士活动的完成情况,对本校名学生的得分情况进行了统计,按照、、、分成组,并绘制了如图所示的频率分布直方图,下列说法正确的是( )
A.图中的值为
B.这组数据的平均数为
C.由图形中的数据,可估计分位数是
D.分以上将获得金牌小卫士称号,则该校有人获得该称号
32.(2021·广东广州·高一期末)为了解学生的身体状况,某校随机抽取了100名学生测量体重,经统计,这些学生的体重数据(单位:千克)全部介于45至70之间,将数据整理得到如图所示的频率分布直方图,则( )
A.频率分布直方图中的值为0.04
B.这100名学生中体重不低于60千克的人数为20
C.这100名学生体重的众数约为52.5
D.据此可以估计该校学生体重的75%分位数约为61.25
33.(2021·全国·高一专题练习)(多选)已知100个数据的75百分位数是9.3,则下列说法不正确的是( )
A.这100个数据中一定有75个数小于或等于9.3
B.把这100个数据从小到大排列后,9.3是第75个数据
C.把这100个数据从小到大排列后,9.3是第75个数据和第76个数据的平均数
D.把这100个数据从小到大排列后,9.3是第75个数据和第74个数据的平均数
34.(2021·全国·高一单元测试)某学校为了调查学生一周在生活方面的支出情况,抽出了一个容量为的样本,其频率分布直方图如图所示,其中支出在内的学生有60人,则下列说法正确的是( )
A.样本中支出在内的频率为0.03
B.样本中支出不少于40元的人数为132
C.n的值为200
D.若该校有2000名学生,则约有600人支出在内
35.(2022·广西钦州·高一期末)某学校为了调查学生在放学后体育运动的情况,抽出了一个容量为的样本,其频率分布直方图如图所示,其中运动时间在分钟内的有72人,则下列说法正确的是( )
A.样本中放学后体育运动时间在分钟的频率为0.36
B.样本中放学后体育运动时间不少于40分钟的人数有132
C.的值为200
D.若该校有1000名学生,则必定有300人放学后体育运动时间在分钟
36.(2021·全国·高一课时练习)(多选)学校为了解新课程标准中提升阅读要求对学生阅读兴趣的影响情况,随机抽取了100名学生进行调查.根据调查结果绘制学生周末阅读时间的频率分布直方图如图所示.若将阅读时间不低于30 min的学生称为阅读霸,则( )
A.抽样表明,该校约有一半学生为阅读霸 B.抽取的100名学生中有50名学生为阅读霸
C.抽取的100名学生中有45名学生为阅读霸 D.抽样表明,该校有50名学生为阅读霸
37.(2021·江苏·高邮市临泽中学高一期末)我国网络购物市场保持较快发展,某电商平台为了精准发展,对某地区市场的个人进行了调查,得到频率分布直方图如图所示,将调查对象的年龄分组为,,,,,,已知年龄在内的调查对象有6人,则下列说法正确的是( )
A.为
B.年龄在内的调查对象有人
C.调查对象中,年龄大于岁的频率是
D.调查对象的年龄不超过岁的频率是
三、填空题
38.(2022·陕西·武功县普集高级中学高一)中小学生的视力状况受到社会的广泛关注,某市有关部门从全市6万名高一学生中随机抽取了400名,对他们的视力状况进行一次调查统计,将所得到的有关数据绘制成频率分布直方图,如图所示.从左至右五个小组的频率之比依次是5:7:12:10:6,则全市高一学生视力在范围内的学生约有_________人.
39.(2022·辽宁朝阳·高一开学考试)某中学为了解学生数学课程的学习情况,在2200名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测这2200名学生在该次数学考试中成绩不小于80分的学生有______人.
40.(2022·全国·高一)某地政府调查了工薪阶层1000人的月工资收入(单位:百元),并把调查结果画成如图所示的频率分布直方图,为了了解工薪阶层对月工资收入的满意程度,要用分层随机抽样的方法从调查的1000人中抽出100人做电话询访,则月工资收入在内的应抽出______人。
41.(2021·全国·高一课时练习)某测试卷的满分为100分,60分及以上为及格.现有100人参加测试,将这100人的卷面分数按照,,,分组后绘制的频率分布直方图如图所示.由于及格人数较少,某位老师准备将每位学生的卷面得分采用“开方乘以10取整”的方法进行换算以提高及格率(实数a的取整为不超过a的最大整数),如:某位学生卷面得分为49分,则换算成70分作为最终考试成绩,则按照这种方法求出的及格率与实际及格率的差是______.
42.(2022·河南焦作·高一期末)某小学制订了一份调查问卷,让学生家长对该校实行“双减”的效果进行评分,评分都在内,将所有数据按,,,,,进行分组,整理得到频率分布直方图如下,则这次调查数据的70%分位数为___________.
43.(2022·全国·高一课时练习)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式,两组工人完成生产任务的工作时间(单位:min)如下:
第一种生产方式所需时间:68,72,76,77,79,82,83,83,84,85,86,87,87,88,89,90,90,91,91,92;第二种生产方式所需时间:65,65,66,68,69,70,71,72,72,73,74,75,76,76,78,81,84,84,85,90.
估计40名工人完成生产任务所需时间数据的第20百分位数为______.
44.(2021·广东广州·高一期末)有10种不同的零食,每100克可食部分包含的能量(单位:)如下:
100,120,125,165,430,190,175,234,425,310
这10种零食每100克可食部分的能量的第60百分位数为___________.
45.(2021·江苏·金陵中学高一阶段练习)甲、乙两名篮球运动员在随机抽取的12场比赛中的得分情况如下:
甲:12,15,20,25,31,31,36,36,37,39,44,49.
乙:8,13,14,16,23,26,28,29,31,38,39,51.
则运动员甲得分的25百分位数与运动员乙得分的80百分位数的和为______.
解答题
46.(2022·江西省铜鼓中学高一开学考试)某校对年高一上学期期中数学考试成绩(单位:分)进行分析,随机抽取名学生,将分数按照,,,,,分成组,制成了如图所示的频率分布直方图:
(1)估计该校高一期中数学考试成绩的平均分;
(2)估计该校高一期中数学考试成绩的第百分位数;
(3)为了进一步了解学生对数学学习的情况,由频率分布直方图,成绩在和的两组中,用按比例分配的分层随机抽样的方法抽取名学生,再从这名学生中随机抽取.名学生进行问卷调查,求抽取的这名学生至少有人成绩在内的概率.
47.(2021·全国·高一课时练习)从某珍珠公司生产的产品中,随机抽取12颗珍珠,得到它们的质量(单位:g)如下:7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0.
(1)求出这组数据的四分位数.
(2)请你找出珍珠质量较小的前15%的珍珠质量.
(3)若用25%,50%,95%分位数把该公司生产的珍珠划分为次品 合格品 优等品和特优品,依照这个样本数据,给出该公司珍珠等级的划分标准.
48.(2021·全国·高一课时练习)从某校500名12岁男孩中用简单随机抽样的方法抽取一个容量为120的身高(单位:cm)样本,具体数据如下表所示:
分组 [122,126) [126,130) [130,134) [134,138) [138,142)
人数 5 8 10 22 33
分组 [142,146) [146,150) [150,154)
人数 20 11 6 5
(1)列出频率分布表;
(2)画出频率直方图;
(3)画出频率折线图;
(4)估计身高小于134cm的人数占总人数的百分比.
49.(2021·全国·高一课时练习)已知某中学高三学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001, 002, …, 800进行编号.
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检查的3个人的编号.
下面摘取了第7行到第9行:
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)被抽取的100人中数学与地理的水平测试成绩的人数分布如下表所示:
数 学
优秀 良好 及格
地理 优秀 7 20 5
良好 9 18 6
及格 a 4 b
成绩分为优秀、良好、及格三个等级;横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的人数为20+18+4=42.若在该样本中,数学成绩的优秀率是30%,求a,b的值.
50.(2022·全国·高一课时练习)“水是生命之源”,但是据科学界统计,可用淡水资源仅占地球储水总量的2.8%,全世界近80%人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(单位:t):一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过随机抽样,获得了某年100位居民每人的月均用水量(单位:t),将数据按照,,,分成9组,制成了如图所示的频率分布直方图.
(1)设该市有60万居民,估计全市居民中月均用水量不低于2.5 t的人数,并说明理由;
(2)若该市政府希望使82%的居民每月的用水不按议价收费,估计x的值,并说明理由.
试卷第1页,共3页
【答案详解】
1.B
【详解】
这种冷饮一天的需求量不超过瓶,当且仅当最高气温低于,
由表格数据可知,最高气温低于的频率为,
所以,月份这种冷饮一天的需求量不超过瓶的概率估计值为,故.
故选:B.
2.B
【详解】
设样本在、内的数据个数分别为
数据在上的频率为
解得:
则样本在、内的数据个数共有:.
故选:B.
3.B
由频率分布表的性质,得:
m=100﹣8﹣10﹣20﹣26﹣16﹣6﹣2=12,故A错误;
∵观看比赛不低于4场的学生所占比率为:16%+12%+6%+2%=36%,
∴估计观看比赛不低于4场的学生约为:1000×36%=360人,故B正确,C错误;
出现频率最高的为3.故D错误;
故选:B.
4.(1)见解析
(2)0.81
【解析】
(1)
经过统计可得
有6天,
有7天
有10天
有13天
有12天
有4天
有7天
由题意知样本容量为20,频率分布表如下:
分组 频数 频率
, 6
, 7
, 10
, 13
, 12
, 4
, 7
合计 59 1
频率分布直方图为:、
(2)
该城市1—2月的日平均气温在0℃以下的天数共为48天
1—2月共有59天
该城市1—2月的日平均气温在0℃以下的天数所占的百分比为
5.(1),频率为;
(2)元.
【解析】
【分析】
(1)根据频率分布直方图中所有小矩形的面积之和为的这个性质进行求解即可;
(2)根据分层抽样的性质进行求解即可.
(1)
由图可知,,
这200个口罩中优等品的频率为.
(2)
因为,所以从中抽取个,从中抽取个,
故这21个口罩的检测总费用为元.
6.(1)
(2)9
(3)不合理,理由见解析
【解析】
【分析】
(1)根据频率分布直方图中,小矩形面积和为求解即可;
(2)首先求学习时间不少于20小时的频率,再根据样本容量乘以频率=人数,计算结果;
(3)结合样本来自同一个班级,故不具有代表性.
(1)
解:因为频率分布直方图中,小矩形面积和为,
所以,解得.
(2)
解:由图可知,该班学生周末的学习时间不少于20小时的频率为
则40名学生中周末的学习时间不少于20小时的人数为 .
(3)
解:不合理,样本的选取只选在高一某班,不具有代表性.
7.D
【解析】
【分析】
根据第p百分位数的定义直接计算,再判断作答.
【详解】
由知,这组数据的分位数是按从小到大排列的第6个位置的数,
所以这组数据的分位数是115.
故选:D
8.D
【解析】
【分析】
根据百分位数的定义计算即可.
【详解】
由小到大排列12个数据为2710,2757,2850,2880,2880,2890,2920,2940,2950,3050,3130,3325;
因为,
所以75%分位数为,
故选:D
9.C
【解析】
【分析】
利用百分位数的含义结合条件即得.
【详解】
∵约70%的居民用电在第一阶梯内,约20%的居民用电在第二阶梯内,
∴由表中数据可得,第二阶梯电价的用电量范围为.
故选:C.
10.B
【解析】
【分析】
由频率分布直方图数据求解
【详解】
由图可得自习时间不足22.5小时的频率为
则人数为
故选:B
11.D
【解析】
【分析】
根据频率分布直方图及,求得a,b,得到各组的人数,再利用分层抽样求解.
【详解】
由频率分布直方图得
解得,,
所以年龄在,,,,,内的人数分别为150,300,350,100,50,50,
利用分层抽样选取的人数分别为3,6,7,2,1,1,
故选:D.
12.C
【解析】
【分析】
先求出血液酒精浓度在80mg/100ml以上的频率,然后用总人数500乘以频率即可得答案
【详解】
由频率分布直方图可知血液酒精浓度在80mg/100ml以上的频率为
,
所以这500人属于醉酒驾车的人数约为
故选:C
13.B
【解析】
【分析】
由频率分布直方图求出可得得分在之间的频率,从而得样本容量.
【详解】
由频率分布直方图,,,
所以得分在之间的频率为,人数为.
故选:B.
14.B
【解析】
【分析】
利用频率组距,即可得解.
【详解】
根据频率分布直方图可知,质量指标值在内的概率
故选:B
15.D
【解析】
【详解】
解析:由题意得,=0.35,解得x=4,则y=20-2-3-4-5-2=4,故所求频率为=0.20.
16.C
【解析】
【分析】
由频数分布表可直接计算求得结果.
【详解】
由频数分布表知:样本数据落在内的频率为.
故选:C.
17.D
【解析】
【分析】
根据频率之和为1可求出.
【详解】
由频率分布直方图可得第四小组的频率为.
故选:D.
18.A
【解析】
【分析】
设第一小组的频率为x,进而根据频率和为1求得,进而根据频率分布直方图求解即可.
【详解】
设第一小组的频率为x,则由频率分布直方图,得.
解得,第二小组的频率为,
第二小组频数为13,抽取的男生人数为.
全校男、女生比例为,
全校抽取的学生人数为.
故选:A.
19.D
【解析】
【分析】
根据频率分布直方图,求出不低于60分的频率即可得出答案
【详解】
解:根据频率分布直方图,
不低于60分的频率为,
所以及格率是.
故选:D.
20.C
【解析】
【分析】
由物理二等奖的人数和频率可得该考场总共人数,乘以化学考试获得一等奖的频率可判断①;计算出全校获得物理考试二等奖的频率和总人数相乘可判断②;采用分层抽样从全校抽取200人,乘以化学考试被淘汰的人数的频率可判断③.
【详解】
由于,所以该考场总共有50人,所以化学考试获得一等奖的有人,所以①正确;全校获得物理考试二等奖的有人,所以②正确;如果采用分层抽样从全校抽取200人,则化学考试被淘汰的人数为人,所以③错误.
故选:C.
21.A
【解析】
【分析】
频率分布直方图中,小矩形的高等于每一组的频率组距,它们与频数成正比,小矩形的面积等于这一组的频率.建立相应的关系式,即可求得.
【详解】
解:从频率分布直方图上可以看出,
,
故选:.
22.C
【解析】
【分析】
根据频率分布直方图的性质,各小矩形面积之和为1,可求出中间一个长方形的面积,再根据频数=样本容量×频率(长方形的面积)即可解出.
【详解】
设中间一个长方形的面积为,所以,解得,即中间一组的频数为.
故选:C.
23.C
【解析】
【分析】
根据分位数的定义即可求得答案.
【详解】
这组数据的60%分位数是.
24.C
【解析】
【分析】
由随机表及编号规则确定抽取的6件产品编号,再从小到大排序,应用百分位数的求法求75%分位数.
【详解】
由题设,依次读取的编号为,
根据编号规则易知:抽取的6件产品编号为,
所以将它们从小到大排序为,
故,所以75%分位数为.
故选:C
25.C
【解析】
【分析】
由频率分布直方图计算,找出累计频率值为0.3处对应的自习时间值即可.
【详解】
由频率分布直方图可知,区间在对应的频率为,区间在对应的频率为,,0.3处对应自习时间值恰为22.5,故这200名学生每周的自习时间数据的第30百分位数为22.5.
故选:C
26.B
【解析】
【分析】
根据题意,结合百分位数的计算方法,即可求解.
【详解】
根据题意,把幸福指数从小到大排列为:3,4,5,5,6,7,8,9,
由,知这组数据的第70百分位数是7.
故选:B.
27.C
【解析】
【详解】
由图可得,,,A选项错误;
甲的成绩的中位数为6,乙的成绩的中位数为5,B选项错误;
,所以甲的成绩的第80百分位数为,乙的成绩的第80百分位数为,C选项正确;
甲的成绩的极差为4,乙的成绩的极差也为4,D选项错误.
故选C.
28.D
【解析】
【分析】
由概率总和为1可得,由百分位数定义计算80%分位数,由频率分布直方图的频率计算人数,均值判断各选项.
【详解】
由得,A错;
成绩在区间[70,80)的频率为,人数为,B错;
低于90分的频率为,设样本数据的80%分位数约为分,
则,解得,C错;
平均成绩为,D正确.
故选:D.
29.C
【解析】
【分析】
利用百分位数的定义求解即可
【详解】
,因为第6个和第7个数据分别为5.5和6.7,
所以估计这24户居民的月均用水量的第25百分位数为.
故选:C
30.A
【解析】
【分析】
共60个数,计算出第75百分位数是第几个,然后从所给数据中找到.
【详解】
,从表中知第45与46两个数的平均值.
故选:A.
31.BC
【解析】
【分析】
由直方图的面积之和为可判断A选项;求出平均数可判断B选项;求出分位数可判断C选项;计算出该校获得金牌小卫士称号的人数可判断D选项.
【详解】
对于A选项,由频率分布直方图可知,解得,A错;
对于B选项,这组数据的平均数为,B对;
对于C选项,,,
所以,设这组数据分位数为,则,则,解得;
对于D选项,由频率分布直方图可知,该校获得金牌小卫士称号的人数为人,D错.
故选:BC.
32.ACD
【解析】
【分析】
利用频率之和为1可判断选项A,利用频率与频数的关系即可判断选项B,利用频率分布直方图中众数的计算方法求解众数,即可判断选项C,由百分位数的计算方法求解,即可判断选项D.
【详解】
解:由,解得,故选项A正确;
体重不低于60千克的频率为,
所以这100名学生中体重不低于60千克的人数为人,故选项B错误;
100名学生体重的众数约为,故选项C正确;
因为体重不低于60千克的频率为0.3,而体重在,的频率为,
所以计该校学生体重的分位数约为,故选项D正确.
故选:ACD.
33.BD
【解析】
【分析】
根据百分位的概念,即可判定,得到答案.
【详解】
因为为整数,所以第75个数据和第76个数据的平均数为第75百分位数9.3,所以A正确,B不正确;C正确;D不正确.
故选:BD.
34.BCD
【解析】
【分析】
根据频率之和为补全频率分布直方图,由此对选项进行分析,从而确定正确选项.
【详解】
设对应小长方形的高为,
,解得.
所以样本中支出在内的频率为,A选项错误.
,C选项正确.
样本中支出不少于40元的人数为,B选项正确.
该校有2000名学生,则约有人支出在内,D选项正确.
故选:BCD
35.ABC
【解析】
【分析】
由频率分布直方图求得运动时间在分钟的频率,从而得出总人数,再计算后判断各选项.
【详解】
由频率分布直方图得运动时间在分钟的频率是,A正确;
所以总人数为.C正确;
运动时间不少于40分钟的人数为,B正确;
若该校有1000名学生,根据样本频率估计总体频率,只能说明可能有300人放学后体育运动时间在分钟,D错误.
故选:ABC.
36.AB
【解析】
【详解】
根据频率直方图可列下表:
阅读时间/min
抽样人数 10 18 22 25 20 5
抽取的100名学生中有50名为阅读霸,据此可判断该校约有一半学生为阅读霸.
故选:AB.
37.ABD
【解析】
【分析】
根据频率分布直方图,利用频率、频数与样本容量的关系即可解答.
【详解】
由题意可得,调查对象的年龄在[25,30)内的频率为0.03×5=0.15,
∵已知年龄在[25,30)内的调查对象有6人,
∴N=,故A选项正确,
∵年龄在[30,35)内的频率是1-(0.01×2+0.02+0.03×2+0.04)×5=0.3,
∴年龄在[30,35)内的调查对象有40×0.3=12人,故B选项正确,
观察频率分布直方图可知,调查对象中年龄大于35岁的频率(0.04+0.03+0.02+0.01)×5=0.5,故C选项错误,
观察频率分布直方图可知,调查对象中年龄超过45岁的频率(0.01+0.02)×5=0.15,
则调查对象的年龄不超过45岁的频率是1-0.15=0.85,故D选项正确.
故选:ABD.
38.7500
【解析】
【分析】
先求出第五小组的频率,进而根据第一小组、第五小组的频率之比,可求出第一小组的频率,进而可求出第一小组的学生人数.
【详解】
由图可知,第五小组的频率为,
又因为从左至右五个小组的频率之比为5∶7∶12∶10∶6,
所以第一小组、第五小组的频率之比为5∶6,
所以第一小组的频率为.
所以该市6万名高一学生中视力在范围内的学生人数约为.
故答案为:7500
39.616
【解析】
【分析】
计算成绩不低于80的两个小矩形的面积之和,即成绩不低于80的学生的频率,再乘以2200即可.
【详解】
.
故答案为:616.
40.
【解析】
【分析】
根据小矩形的面积之和等于求出区间的小矩形的面积即为该组的频率,再由该频率乘以即可求解.
【详解】
由频率分布直方图可知月工资收入在内的频率为:
,
所以用分层抽样抽出的100人做电话询访,月工资收入在内的频率为,
则月工资收入在内的应抽出人,
故答案为:.
41.0.52
【解析】
【分析】
根据换算方法,及格率与实际及格率的差是内的频率求解.
【详解】
由频率分布直方图,得卷面得分在内的频率为:,
所以按照这种方式求出的及格率与实际及格率的差是0.52.
故答案为:0.52
42.80
【解析】
【分析】
利用百分位数的概念以及频率分布直方图求解..
【详解】
因为前4组数据的频率之和为0.05+0.15+0.2+0.3=0.7,
所以70%分位数为80.
故答案为:80
43.##
【解析】
【分析】
根据题意,结合百分位数的计算方法,即可求解.
【详解】
根据题意,将这40个数据从小到大排列,如下所述,
65,65,66,68,68,69,70,71,72,72,72,73,74,75,76,76,76,77,78,79,
81,82,83,83,84,84,84,85,85,86,87,87,88,89,90,90,90,91,91,92,
由,可知第20百分位数为第8项数据与第9项数据的平均数.
故答案为:.
44.212
【解析】
【分析】
先将数据从小到大排,然后由确定第60百分位数.
【详解】
根据题意,将10个数据从小到大排列:
100,120,125,165,175,190,234,310,425,430;
,
则该组数据的第60百分位数为,
故答案为:212.
45.
【解析】
【分析】
根据百分位数的计算规则计算可得;
【详解】
解:因为,故运动员甲得分的25百分位数为从小到大排列的第3和4个数的平均数,为;
又,所以运动员乙得分的80百分位数为从小到大排列的第10个数,为,所以
故答案为:
46.(1)分;
(2)分;
(3).
【解析】
【分析】
先利用频率之和为,计算出,进而求出平均值即可;
利用百分位数的运算方法,求出成绩的第百分位数;
利用分层抽样取样方法,算出需在分数段内抽人,分别记为,,需在分数段内抽人,分别记为,,,写出样本空间和符合条件样本点数,即可求出相应概率.
(1)
解:由,
得.
数学成绩在:
频率,
频率,
频率,
频率,
频率,
频率,
样本平均值为:,
可以估计样本数据中数学成绩均值为分,
据此可以估计该校高一下学期期中数学考试成绩估计分.
(2)
解:由知样本数据中数学考试成绩在分以下所占比例为,
在分以下所占比例为
因此,第百分位数一定位于内,由,
可以估计样本数据的第百分位数约为分,
据此可以估计该校高一下学期期中数学考试成绩第百分位数约为分.
(3)
解:由题意可知,分数段的人数为 (人),
分数段的人数为 (人).
用按比例分配的分层随机抽样的方法抽取名学生,则需在分数段内抽人,分别记为,,需在分数段内抽人,分别记为,,,
设“从样本中任取人,至少有人在分数段内”为事件,
则样本空间共包含个样本点
而的对立事件包含个样本点
所以,所以,即抽取的这名学生至少有人在内的概率为.
47.(1)8.15,8.5,8.75
(2)7.8g,7.9g.
(3)答案见解析
【解析】
【分析】
(1)将所有数据从小到大排列,由四分位数的定义求解即可;
(2)由,得出产品质量较小的前15%的产品有2个;
(3)先计算95%分位数,再根据25%,50%,95%分位数将珍珠等级进行划分.
(1)
将所有数据从小到大排列,得
7.8,7.9,8.0,8.3,8.4,8.5,8.5,8.5,8.6,8.9,9.0,9.9,
因为共有12个数据,,,,
所以25%分位数是,
50%分位数是,
75%分位数是.
故这组数据的四分位数分别为8.15,8.5,8.75.
(2)
因为共有12个数据,,
所以产品质量较小的前15%的产品有2个,它们的质量分别为7.8g,7.9g.
(3)
由(1)可知样本数据的25%分位数是8.15,50%分位数是8.5
因为,所以95%分位数是第12个数据,即9.9,
所以质量小于等于8.15g的珍珠为次品,质量大于8.15g且小于等于8.5g的珍珠为合格品,质量大于8.5g且小于等于9.9g的珍珠为优等品,质量大于9.9g的珍珠为特优品.
48.(1)频率分布表见解析
(2)频率直方图见解析
(3)频率折线图见解析
(4)19%
【解析】
【分析】
(1)根据所给数据列出频率分布表;
(2)由频率分布表画出频率分布直方图;
(3)由频率分布直方图画出频率分布折线图
(4)由频率分布表可得身高小于134 cm的学生的频率;
(1)
频率分布表如下表所示:
分组 频数 频率
[122,126) 5 0.04 0.01
[126,130) 8 0.07 0.0175
[130,134) 10 0.08 0.02
[134,138) 22 0.18 0.045
[138,142) 33 0.28 0.07
[142,146) 20 0.17 0.0425
[146,150) 11 0.09 0.0225
[150,154) 6 0.05 0.0125
[154,158) 5 0.04 0.01
合计 120 1 0.25
(2)
(3)
(4)
由频率分布表可知身高小于134cm的男孩出现的频率为0.04+0.07+0.08=0.19,所以身高小于134cm的人数约占总人数的19%.
49.(1)785,567,199
(2)a=14, b=17
【解析】
【分析】
(1)根据随机数表的抽样方法抽出数据即可;
(2)由总人数100和数学成绩的优秀率为30%列出方程组,进而解得答案即可.
(1)
根据题意,抽取的数字需在编号001,002,…,800之内,且重复的数字需要剔除,第一个抽取的数字是785,而916,955不满足,接着是567,199,满足题意,即抽取的前3个数字是785,567,199.
(2)
根据题意,,且,
解得:.
50.(1)估计全市居民中月均用水量不低于2.5 t的人数为(万),理由见解析
(2)估计x的值为2.8,理由见解析
【解析】
(1)
由题图可知,不低于2.5 t人数所占百分比为,
所以估计全市居民中月均用水量不低于2.5 t的人数为(万).
(2)
由(1)可知,月均用水量小于2.5 t的居民人数所占百分比为73%,
即73%的居民月均用水量小于2.5 t,
则73%+
所以88%的居民月均用水量小于3 t,故,
所以.
故估计x的值为2.8.
9.2.1 总体取值规律的估计-9.2.2总体百分位数的估计 同步精练
【考点梳理】
考点一:频率分布直方图
作频率分布直方图的步骤
1.求极差:极差为一组数据中最大值与最小值的差.
2.决定组距与组数
将数据分组时,一般取等长组距,并且组距应力求“取整”,组数应力求合适,以使数据的分布规律能较清楚地呈现出来.
3.将数据分组
4.列频率分布表
各小组的频率=.
5.画频率分布直方图
纵轴表示,实际上就是频率分布直方图中各小长方形的高度,小长方形的面积=组距×=频率.
技巧归纳:
(1)分点的决定方法:若数据为整数,则减去0.5作为分点数;若数据是小数点后一位的数,则减去0.05作为分点数;依次类推.
(2)画频率分布直方图中小矩形的高的方法:①小矩形的高=;②假设频数为1的小矩形的高为h,则频数为k的小矩形的高为kh.
(3)频率分布直方图的性质
①因为小矩形的面积=组距×=频率,所以各小矩形的面积表示相应各组的频率.这样,频率分布直方图就以面积的形式反映了数据落在各个小组内的频率大小.
②在频率分布直方图中,各小矩形的面积之和等于1.
③=样本容量.
(2)频率分布直方图反映了样本在各个范围内取值的可能性,由抽样的代表性利用样本在某一范围内的频率,可近似地估计总体在这一范围内的可能性.
考点二:常见统计图表的特点与区别
扇形图主要用于直观描述各类数据占总数的比例,条形图和直方图主要用于直观描述不同类别或分组数据的频数和频率,条形图适用于描述离散型数据,直方图适用于描述连续型数据.折线图主要用于描述数据随时间的变化趋势.
考点三:百分位数
1.百分位数定义:一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
2.常用的百分位数
(1)四分位数:第25百分位数,第50百分位数,第75百分位数.
(2)其它常用的百分位数:第1百分位数,第5百分位数,第95百分位数,第99百分位数.
3.计算一组n个数据的第p百分位数的一般步骤如下:
第1步,按从小到大排列原始数据;
第2步,计算i=n×p%;
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
【题型归纳】
题型一:频率分布概念的理解
1.(2021·全国·高一专题练习)某超市计划按月订购一种冷饮,根据往年销售经验,每天需求量与当天最高气温(单位:)有关.如果最高气温不低于,需求量为瓶;如果最高气温位于区间(单位:)内,需求量为瓶;如果最高气温低于,需求量为瓶.为了确定月份的订购计划,统计了前三年月份各天的最高气温数据,得到下面的频数分布表:
最高气温
天数
将最高气温位于各区间的频率视为最高气温位于该区间的概率,若月份这种冷饮一天的需求量不超过瓶的概率估计值为,则( )
A. B. C. D.
2.(2020·江苏·海安高级中学高一期中)一个班数学成绩频率分布表(样本容量为)不小心损坏了一部分,只记得样本中数据在上的频率为,则估计样本在、内的数据个数共有( )
分组
频数
A.28 B.30 C.32 D.34
3.(2020·天津河西·高一期中)在“世界杯”足球赛闭幕后,某中学学生会对本校高一年级1000名学生收看比赛的情况用随机抽样方式进行调查,样本容量为50,将数据分组整理后,列表如表:
观看场数 0 1 2 3 4 5 6 7
观看人数占调查人数的百分比 8% 10% 20% 26% m% 12% 6% 2%
从表中可以得出正确的结论为( )
A.表中m的数值为8 B.估计观看比赛不低于4场的学生约为360人
C.估计观看比赛不低于4场的学生约为720人 D.估计观看比赛场数的众数为2
题型二:画频率分布直方图
4.(2022·湖南·高一)下面是北方某城市2018年1—2月的日平均气温(单位:℃)的记录数据:
2 7 8 9
0 5
0 5
2 7 5
(1)将数据适当分组,并画出相应的频率分布直方图;
(2)试估计该城市1—2月的日平均气温在0℃以下的天数所占的百分比.
5.(2022·辽宁朝阳·高一)一次性医用口罩是适用于覆盖使用者的口 鼻及下颌,用于普通医疗环境中阻隔口腔和鼻腔呼出或喷出污染物的一次性口罩.按照我国医药行业标准,口罩对细菌的过滤效率达到95%及以上为合格,98%及以上为优等品.某部门为了检测一批口罩对细菌的过滤效率,随机抽检了200个口罩,将它们的过滤效率(百分比)按照,,,,分成5组,制成如图所示的频率分布直方图.
(1)求图中m的值及这200个口罩中优等品的频率;
(2)为了进一步检测样本中优等品的质量,用分层抽样的方法从和两组中抽取21个口罩,已知过滤效率百分比低于99%的检测费为每个8元,不低于99%的检测费为每个12元,求这21个口罩的检测总费用.
6.(2022·北京师大附中高一期末)为了解学生的周末学习时间(单位:小时),高一年级某班班主任对本班40名学生某周末的学习时间进行了调查,将所得数据整理绘制出如图所示的频率分布直方图,根据直方图所提供的信息:
(1)求出图中a的值;
(2)求该班学生这个周末的学习时间不少于20小时的人数;
(3)如果用该班学生周末的学习时间作为样本去推断该校高一年级全体学生周末的学习时间,这样推断是否合理?说明理由.
题型三:总体百分数的估算
7.(2022·贵州遵义·高一期末)某数学老师记录了班上8名同学的数学考试成绩,得到如下数据:90,98,100,108,111,115,115,125.则这组数据的分位数是( )
A.100 B.111 C.113 D.115
8.(2022·江西·景德镇一中高一期末)下表为12名毕业生的起始月薪:
毕业生 1 2 3 4 5 6 7 8 9 10 11 12
起始月薪 2850 2950 3050 2880 2755 2710 2890 3130 2940 3325 2920 2880
根据表中所给的数据计算75%分位数为( )
A.2950 B.3050 C.3130 D.3000
9.(2022·辽宁丹东·高一期末)某地区想实行阶梯电价,经调查发现,该地区居民用电量信息如下:
分位数 50%分位数 70%分位数 80%分位数 90%分位数
用电量 160 176 215 230
如果要求约70%的居民用电在第一阶梯内,约20%的居民用电在第二阶梯内,可确定第二阶梯电价的用电量范围为( )
A. B. C. D.
题型四:频率分布直方图的性质
10.(2022·天津河北·一模)某高校调查了400名学生每周的自习时间(单位:小时),绘制成如图所示的频率分布直方图,其中自习时间的范围是,样本数据分组为,,,,.则根据直方图这400名学生中每周的自习时间不足22.5小时的人数是( )
A.60 B.90 C.130 D.150
11.(2022·陕西·武功县普集高级中学高一阶段练习)为了研究人们生活健康情况,某市随机选取年龄在15~75岁之间的1000人进行调查,得到频率分布直方图如图所示,其中,利用分层抽样从年龄在,,,,,之间共选取20名市民书写生活健康的报告,其中选取年龄在市民的人数为( )
A.2 B.3 C.4 D.7
12.(2021·全国·高一课时练习)根据《中华人民共和国道路交通安全法》规定:血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车,处十五日以下拘留和三个月以上六个月以下暂扣驾驶证,并处500元以上2000元以下罚款.据《法制晚报》报道,2009年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共500人.如图,这是对这500人酒后驾车血液中酒精含量进行检测所得结果的频率直方图,则属于醉酒驾车的人数约为( )
A.25 B.50 C.75 D.100
【双基达标】
一、单选题
13.(2022·陕西·西安市阎良区关山中学高一阶段练习)在一次高二数学单元评估中,共有500名同学参加调研测试,经过评估,这500名学生的得分都在之间,其得分的频率分布直方图如图,则得分在之间的学生人数是( )
A.150 B.200 C.250 D.300
14.(2022·陕西·武功县普集高级中学高一阶段练习)为保障食品安全,某监管部门对辖区内一家食品企业进行检查,现从其生产的某种产品中随机抽取100件作为样本,并以产品的一项关键质量指标值为检测依据,整理得到如下的样本频率分布直方图.若质量指标值在内的产品为一等品,则该企业生产的产品为一等品的概率约为( )
A.0.38 B.0.61
C.0.122 D.0.75
15.(2021·江西上饶·高一阶段练习)采用简单随机抽样抽到一个容量为20的样本数据,分组后,各组的频数如下表:
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70)
频数 2 3 x 5 y 2
已知样本数据在区间[20,40)内的频率为0.35,则样本数据在区间[50,60)内的频率为( )
A.0.70 B.0.50 C.0.25 D.0.20
16.(2021·全国·高一单元测试)一个容量为的样本,其数据的分组与各组的频数如下:
分组
频数
则样本数据落在内的频率为( )
A. B. C. D.
17.(2021·甘肃·嘉峪关市第一中学高一期中)在高一(1)班组织的“我爱古诗词”的调研考试中,全班40名学生的成绩数据(均为整数且都在)统计为如下的频率分布直方图,则第四小组(成绩分布在)的频率为( )
A.0.001 B.0.01 C.0.03 D.0.3
18.(2021·陕西铜川·高一期中)某校将举办秋季体育文化节,为了解该校学生的身体状况,抽取部分男生和女生的体重,将男生体重数据整理后,作出了频率分布直方图,已知图中从左到右前三个小组频率之比为,第二小组频数为13,若全校男、女生比例为,则全校抽取的学生人数为( )
A.100 B.80 C.45 D.32
19.(2021·陕西渭南·高一期末)抽样统计某校部分学生的物理测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是( )
A. B.
C. D.
20.(2021·全国·高一课时练习)某个高级中学组织物理 化学学科能力竞赛,全校1000名学生都参加两科考试,考试后按学科分别评出一 二 三等奖和淘汰的这四个等级,现有某考场的两科考试数据统计如下,其中物理科目成绩为二等奖的考生有12人.如果以这个考场考生的物理和化学成绩去估计全校考生的物理和化学成绩分布,则以下说法正确的是( )
①该考场化学考试获得一等奖的有4人;
②全校物理考试获得二等奖的有240人;
③如果采用分层抽样从全校抽取200人,则化学考试被淘汰78人.
A.①②③ B.②③ C.①② D.①③
21.(2021·陕西铜川·高一期末)某班50名学生在一次百米测试中,成绩全部不小于13秒且小于19秒,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…;第六组,成绩大于等于18秒且小于19秒,如图是按上述分组方法得到的频率分布直方图,设成绩小于17秒的学生人数占全班总人数的百分比为,成绩大于等于15秒且小于17秒的学生人数为,则从频率分布直方图中可分析出和的值分别是( )
A.,35 B.,45
C.,35 D.,45
【高分突破】
一:单选题
22.(2021·黑龙江·大庆市东风中学高一期末)在样本的频率分布直方图中,共有5个小长方形,若中间一个长方形的面积等于其他4个小长方形面积和的,且样本容量为210,则中间一组的频数为( )
A.10 B.20 C.60 D.70
23.(2022·河南南阳·高一期末)体育老师记录了班上10名同学1分钟内的跳绳次数,得到如下数据:88,94,96,98,98,99,100,101,101,116.这组数据的60%分位数是( )
A.98 B.99 C.99.5 D.100
24.(2021·辽宁·高一期末)从800件产品中抽取6件进行质检,利用随机数表法抽取样本时,先将800件产品按001,002,…,800进行编号.如果从随机数表第8行第8列的数8开始往右读数(随机数表第7行至第9行的数如下),则抽取的6件产品的编号的75%分位数是( )
……
8442175331 5724550688 77047447672176335025 8392120676
6301637859 1695566711 69105671751286735807 4439523879
3321123429 7864560782 52420744381551001342 9966027954
A.105 B.556 C.671 D.169
25.(2022·全国·高一课时练习)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是,样本数据分组为,,,,.根据频率分布直方图,估计这200名学生每周的自习时间数据的第30百分位数为( )
A.22 B.21.25 C.22.5 D.25
26.(2021·河北·衡水市冀州区第一中学高一期末)幸福指数是某个人主观地评价他对自己目前生活状态的满意程度指标,常用内的一个数来表示,该数越接近10表示满意程度越高.现随机抽取8位小区居民,他们的幸福指数分别是3,4,5,6,7,8,9,5,则这组数据的第70百分位数是( )
A.6 B.7 C.7.5 D.8
27.(2021·全国·高一课前预习)甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则( )
A.甲的成绩的平均数小于乙的成绩的平均数
B.甲的成绩的中位数等于乙的成绩的中位数
C.甲的成绩的第80百分位数等于乙的成绩的第80百分位数
D.甲的成绩的极差大于乙的成绩的极差
28.(2021·全国·高一课前预习)某校组织全体学生参加了主题为“建党百年,薪火相传”的知识竞赛,随机抽取了200名学生进行成绩统计,发现抽取的学生的成绩都在50分至100分之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示,下列说法正确的是( )
A.直方图中的值为0.004
B.在被抽取的学生中,成绩在区间[70,80)的学生数为15人
C.估计全校学生成绩的样本数据的80%分位数约为93分
D.估计全校学生的平均成绩为84分
29.(2022·全国·高一专题练习)通过抽样调查得到某栋居民楼24户居民的月均用水量数量(单位:),将其按从小到大排序如下:
2.1 3.2 3.2 4.3 4.3 5.5 6.7 8.9 9.4 9.5 9.5 9.9
10.1 10.5 11.1 11.2 12.5 14.8 15.2 15.3 18.4 19.0 20.8 22.4
则估计这24户居民的月均用水量的第25百分位数为( )
A.4.3 B.5.5 C.6.1 D.6.7
30.(2021·广东佛山·高一期末)棉花的纤维长度是棉花质量的重要指标,在一批棉花中随机抽到了60根棉花的纤维长度(单位:mm),按从小到大排序结果如下:
25 28 33 50 52 58 59 60 61 62 82 86 113 115 140 143 146 170 175 195 202 206 233 236 238 255 260 263 264 265 293 293 294 296 301 302 303 305 305 306 321 323 325 326 328 340 343 346 348 350 352 355 357 357 358 360 370 380 383 385.
请你估算这批棉花的第75百分位数是( )
A.334 B.327 C.328 D.329
二、多选题
31.(2022·安徽蚌埠·高一期末)某市为了考察一所高中全体学生参与第六届全国中小学生“学宪法、讲宪法”宪法小卫士活动的完成情况,对本校名学生的得分情况进行了统计,按照、、、分成组,并绘制了如图所示的频率分布直方图,下列说法正确的是( )
A.图中的值为
B.这组数据的平均数为
C.由图形中的数据,可估计分位数是
D.分以上将获得金牌小卫士称号,则该校有人获得该称号
32.(2021·广东广州·高一期末)为了解学生的身体状况,某校随机抽取了100名学生测量体重,经统计,这些学生的体重数据(单位:千克)全部介于45至70之间,将数据整理得到如图所示的频率分布直方图,则( )
A.频率分布直方图中的值为0.04
B.这100名学生中体重不低于60千克的人数为20
C.这100名学生体重的众数约为52.5
D.据此可以估计该校学生体重的75%分位数约为61.25
33.(2021·全国·高一专题练习)(多选)已知100个数据的75百分位数是9.3,则下列说法不正确的是( )
A.这100个数据中一定有75个数小于或等于9.3
B.把这100个数据从小到大排列后,9.3是第75个数据
C.把这100个数据从小到大排列后,9.3是第75个数据和第76个数据的平均数
D.把这100个数据从小到大排列后,9.3是第75个数据和第74个数据的平均数
34.(2021·全国·高一单元测试)某学校为了调查学生一周在生活方面的支出情况,抽出了一个容量为的样本,其频率分布直方图如图所示,其中支出在内的学生有60人,则下列说法正确的是( )
A.样本中支出在内的频率为0.03
B.样本中支出不少于40元的人数为132
C.n的值为200
D.若该校有2000名学生,则约有600人支出在内
35.(2022·广西钦州·高一期末)某学校为了调查学生在放学后体育运动的情况,抽出了一个容量为的样本,其频率分布直方图如图所示,其中运动时间在分钟内的有72人,则下列说法正确的是( )
A.样本中放学后体育运动时间在分钟的频率为0.36
B.样本中放学后体育运动时间不少于40分钟的人数有132
C.的值为200
D.若该校有1000名学生,则必定有300人放学后体育运动时间在分钟
36.(2021·全国·高一课时练习)(多选)学校为了解新课程标准中提升阅读要求对学生阅读兴趣的影响情况,随机抽取了100名学生进行调查.根据调查结果绘制学生周末阅读时间的频率分布直方图如图所示.若将阅读时间不低于30 min的学生称为阅读霸,则( )
A.抽样表明,该校约有一半学生为阅读霸 B.抽取的100名学生中有50名学生为阅读霸
C.抽取的100名学生中有45名学生为阅读霸 D.抽样表明,该校有50名学生为阅读霸
37.(2021·江苏·高邮市临泽中学高一期末)我国网络购物市场保持较快发展,某电商平台为了精准发展,对某地区市场的个人进行了调查,得到频率分布直方图如图所示,将调查对象的年龄分组为,,,,,,已知年龄在内的调查对象有6人,则下列说法正确的是( )
A.为
B.年龄在内的调查对象有人
C.调查对象中,年龄大于岁的频率是
D.调查对象的年龄不超过岁的频率是
三、填空题
38.(2022·陕西·武功县普集高级中学高一)中小学生的视力状况受到社会的广泛关注,某市有关部门从全市6万名高一学生中随机抽取了400名,对他们的视力状况进行一次调查统计,将所得到的有关数据绘制成频率分布直方图,如图所示.从左至右五个小组的频率之比依次是5:7:12:10:6,则全市高一学生视力在范围内的学生约有_________人.
39.(2022·辽宁朝阳·高一开学考试)某中学为了解学生数学课程的学习情况,在2200名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测这2200名学生在该次数学考试中成绩不小于80分的学生有______人.
40.(2022·全国·高一)某地政府调查了工薪阶层1000人的月工资收入(单位:百元),并把调查结果画成如图所示的频率分布直方图,为了了解工薪阶层对月工资收入的满意程度,要用分层随机抽样的方法从调查的1000人中抽出100人做电话询访,则月工资收入在内的应抽出______人。
41.(2021·全国·高一课时练习)某测试卷的满分为100分,60分及以上为及格.现有100人参加测试,将这100人的卷面分数按照,,,分组后绘制的频率分布直方图如图所示.由于及格人数较少,某位老师准备将每位学生的卷面得分采用“开方乘以10取整”的方法进行换算以提高及格率(实数a的取整为不超过a的最大整数),如:某位学生卷面得分为49分,则换算成70分作为最终考试成绩,则按照这种方法求出的及格率与实际及格率的差是______.
42.(2022·河南焦作·高一期末)某小学制订了一份调查问卷,让学生家长对该校实行“双减”的效果进行评分,评分都在内,将所有数据按,,,,,进行分组,整理得到频率分布直方图如下,则这次调查数据的70%分位数为___________.
43.(2022·全国·高一课时练习)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式,两组工人完成生产任务的工作时间(单位:min)如下:
第一种生产方式所需时间:68,72,76,77,79,82,83,83,84,85,86,87,87,88,89,90,90,91,91,92;第二种生产方式所需时间:65,65,66,68,69,70,71,72,72,73,74,75,76,76,78,81,84,84,85,90.
估计40名工人完成生产任务所需时间数据的第20百分位数为______.
44.(2021·广东广州·高一期末)有10种不同的零食,每100克可食部分包含的能量(单位:)如下:
100,120,125,165,430,190,175,234,425,310
这10种零食每100克可食部分的能量的第60百分位数为___________.
45.(2021·江苏·金陵中学高一阶段练习)甲、乙两名篮球运动员在随机抽取的12场比赛中的得分情况如下:
甲:12,15,20,25,31,31,36,36,37,39,44,49.
乙:8,13,14,16,23,26,28,29,31,38,39,51.
则运动员甲得分的25百分位数与运动员乙得分的80百分位数的和为______.
解答题
46.(2022·江西省铜鼓中学高一开学考试)某校对年高一上学期期中数学考试成绩(单位:分)进行分析,随机抽取名学生,将分数按照,,,,,分成组,制成了如图所示的频率分布直方图:
(1)估计该校高一期中数学考试成绩的平均分;
(2)估计该校高一期中数学考试成绩的第百分位数;
(3)为了进一步了解学生对数学学习的情况,由频率分布直方图,成绩在和的两组中,用按比例分配的分层随机抽样的方法抽取名学生,再从这名学生中随机抽取.名学生进行问卷调查,求抽取的这名学生至少有人成绩在内的概率.
47.(2021·全国·高一课时练习)从某珍珠公司生产的产品中,随机抽取12颗珍珠,得到它们的质量(单位:g)如下:7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0.
(1)求出这组数据的四分位数.
(2)请你找出珍珠质量较小的前15%的珍珠质量.
(3)若用25%,50%,95%分位数把该公司生产的珍珠划分为次品 合格品 优等品和特优品,依照这个样本数据,给出该公司珍珠等级的划分标准.
48.(2021·全国·高一课时练习)从某校500名12岁男孩中用简单随机抽样的方法抽取一个容量为120的身高(单位:cm)样本,具体数据如下表所示:
分组 [122,126) [126,130) [130,134) [134,138) [138,142)
人数 5 8 10 22 33
分组 [142,146) [146,150) [150,154)
人数 20 11 6 5
(1)列出频率分布表;
(2)画出频率直方图;
(3)画出频率折线图;
(4)估计身高小于134cm的人数占总人数的百分比.
49.(2021·全国·高一课时练习)已知某中学高三学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001, 002, …, 800进行编号.
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检查的3个人的编号.
下面摘取了第7行到第9行:
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)被抽取的100人中数学与地理的水平测试成绩的人数分布如下表所示:
数 学
优秀 良好 及格
地理 优秀 7 20 5
良好 9 18 6
及格 a 4 b
成绩分为优秀、良好、及格三个等级;横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的人数为20+18+4=42.若在该样本中,数学成绩的优秀率是30%,求a,b的值.
50.(2022·全国·高一课时练习)“水是生命之源”,但是据科学界统计,可用淡水资源仅占地球储水总量的2.8%,全世界近80%人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(单位:t):一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过随机抽样,获得了某年100位居民每人的月均用水量(单位:t),将数据按照,,,分成9组,制成了如图所示的频率分布直方图.
(1)设该市有60万居民,估计全市居民中月均用水量不低于2.5 t的人数,并说明理由;
(2)若该市政府希望使82%的居民每月的用水不按议价收费,估计x的值,并说明理由.
试卷第1页,共3页
【答案详解】
1.B
【详解】
这种冷饮一天的需求量不超过瓶,当且仅当最高气温低于,
由表格数据可知,最高气温低于的频率为,
所以,月份这种冷饮一天的需求量不超过瓶的概率估计值为,故.
故选:B.
2.B
【详解】
设样本在、内的数据个数分别为
数据在上的频率为
解得:
则样本在、内的数据个数共有:.
故选:B.
3.B
由频率分布表的性质,得:
m=100﹣8﹣10﹣20﹣26﹣16﹣6﹣2=12,故A错误;
∵观看比赛不低于4场的学生所占比率为:16%+12%+6%+2%=36%,
∴估计观看比赛不低于4场的学生约为:1000×36%=360人,故B正确,C错误;
出现频率最高的为3.故D错误;
故选:B.
4.(1)见解析
(2)0.81
【解析】
(1)
经过统计可得
有6天,
有7天
有10天
有13天
有12天
有4天
有7天
由题意知样本容量为20,频率分布表如下:
分组 频数 频率
, 6
, 7
, 10
, 13
, 12
, 4
, 7
合计 59 1
频率分布直方图为:、
(2)
该城市1—2月的日平均气温在0℃以下的天数共为48天
1—2月共有59天
该城市1—2月的日平均气温在0℃以下的天数所占的百分比为
5.(1),频率为;
(2)元.
【解析】
【分析】
(1)根据频率分布直方图中所有小矩形的面积之和为的这个性质进行求解即可;
(2)根据分层抽样的性质进行求解即可.
(1)
由图可知,,
这200个口罩中优等品的频率为.
(2)
因为,所以从中抽取个,从中抽取个,
故这21个口罩的检测总费用为元.
6.(1)
(2)9
(3)不合理,理由见解析
【解析】
【分析】
(1)根据频率分布直方图中,小矩形面积和为求解即可;
(2)首先求学习时间不少于20小时的频率,再根据样本容量乘以频率=人数,计算结果;
(3)结合样本来自同一个班级,故不具有代表性.
(1)
解:因为频率分布直方图中,小矩形面积和为,
所以,解得.
(2)
解:由图可知,该班学生周末的学习时间不少于20小时的频率为
则40名学生中周末的学习时间不少于20小时的人数为 .
(3)
解:不合理,样本的选取只选在高一某班,不具有代表性.
7.D
【解析】
【分析】
根据第p百分位数的定义直接计算,再判断作答.
【详解】
由知,这组数据的分位数是按从小到大排列的第6个位置的数,
所以这组数据的分位数是115.
故选:D
8.D
【解析】
【分析】
根据百分位数的定义计算即可.
【详解】
由小到大排列12个数据为2710,2757,2850,2880,2880,2890,2920,2940,2950,3050,3130,3325;
因为,
所以75%分位数为,
故选:D
9.C
【解析】
【分析】
利用百分位数的含义结合条件即得.
【详解】
∵约70%的居民用电在第一阶梯内,约20%的居民用电在第二阶梯内,
∴由表中数据可得,第二阶梯电价的用电量范围为.
故选:C.
10.B
【解析】
【分析】
由频率分布直方图数据求解
【详解】
由图可得自习时间不足22.5小时的频率为
则人数为
故选:B
11.D
【解析】
【分析】
根据频率分布直方图及,求得a,b,得到各组的人数,再利用分层抽样求解.
【详解】
由频率分布直方图得
解得,,
所以年龄在,,,,,内的人数分别为150,300,350,100,50,50,
利用分层抽样选取的人数分别为3,6,7,2,1,1,
故选:D.
12.C
【解析】
【分析】
先求出血液酒精浓度在80mg/100ml以上的频率,然后用总人数500乘以频率即可得答案
【详解】
由频率分布直方图可知血液酒精浓度在80mg/100ml以上的频率为
,
所以这500人属于醉酒驾车的人数约为
故选:C
13.B
【解析】
【分析】
由频率分布直方图求出可得得分在之间的频率,从而得样本容量.
【详解】
由频率分布直方图,,,
所以得分在之间的频率为,人数为.
故选:B.
14.B
【解析】
【分析】
利用频率组距,即可得解.
【详解】
根据频率分布直方图可知,质量指标值在内的概率
故选:B
15.D
【解析】
【详解】
解析:由题意得,=0.35,解得x=4,则y=20-2-3-4-5-2=4,故所求频率为=0.20.
16.C
【解析】
【分析】
由频数分布表可直接计算求得结果.
【详解】
由频数分布表知:样本数据落在内的频率为.
故选:C.
17.D
【解析】
【分析】
根据频率之和为1可求出.
【详解】
由频率分布直方图可得第四小组的频率为.
故选:D.
18.A
【解析】
【分析】
设第一小组的频率为x,进而根据频率和为1求得,进而根据频率分布直方图求解即可.
【详解】
设第一小组的频率为x,则由频率分布直方图,得.
解得,第二小组的频率为,
第二小组频数为13,抽取的男生人数为.
全校男、女生比例为,
全校抽取的学生人数为.
故选:A.
19.D
【解析】
【分析】
根据频率分布直方图,求出不低于60分的频率即可得出答案
【详解】
解:根据频率分布直方图,
不低于60分的频率为,
所以及格率是.
故选:D.
20.C
【解析】
【分析】
由物理二等奖的人数和频率可得该考场总共人数,乘以化学考试获得一等奖的频率可判断①;计算出全校获得物理考试二等奖的频率和总人数相乘可判断②;采用分层抽样从全校抽取200人,乘以化学考试被淘汰的人数的频率可判断③.
【详解】
由于,所以该考场总共有50人,所以化学考试获得一等奖的有人,所以①正确;全校获得物理考试二等奖的有人,所以②正确;如果采用分层抽样从全校抽取200人,则化学考试被淘汰的人数为人,所以③错误.
故选:C.
21.A
【解析】
【分析】
频率分布直方图中,小矩形的高等于每一组的频率组距,它们与频数成正比,小矩形的面积等于这一组的频率.建立相应的关系式,即可求得.
【详解】
解:从频率分布直方图上可以看出,
,
故选:.
22.C
【解析】
【分析】
根据频率分布直方图的性质,各小矩形面积之和为1,可求出中间一个长方形的面积,再根据频数=样本容量×频率(长方形的面积)即可解出.
【详解】
设中间一个长方形的面积为,所以,解得,即中间一组的频数为.
故选:C.
23.C
【解析】
【分析】
根据分位数的定义即可求得答案.
【详解】
这组数据的60%分位数是.
24.C
【解析】
【分析】
由随机表及编号规则确定抽取的6件产品编号,再从小到大排序,应用百分位数的求法求75%分位数.
【详解】
由题设,依次读取的编号为,
根据编号规则易知:抽取的6件产品编号为,
所以将它们从小到大排序为,
故,所以75%分位数为.
故选:C
25.C
【解析】
【分析】
由频率分布直方图计算,找出累计频率值为0.3处对应的自习时间值即可.
【详解】
由频率分布直方图可知,区间在对应的频率为,区间在对应的频率为,,0.3处对应自习时间值恰为22.5,故这200名学生每周的自习时间数据的第30百分位数为22.5.
故选:C
26.B
【解析】
【分析】
根据题意,结合百分位数的计算方法,即可求解.
【详解】
根据题意,把幸福指数从小到大排列为:3,4,5,5,6,7,8,9,
由,知这组数据的第70百分位数是7.
故选:B.
27.C
【解析】
【详解】
由图可得,,,A选项错误;
甲的成绩的中位数为6,乙的成绩的中位数为5,B选项错误;
,所以甲的成绩的第80百分位数为,乙的成绩的第80百分位数为,C选项正确;
甲的成绩的极差为4,乙的成绩的极差也为4,D选项错误.
故选C.
28.D
【解析】
【分析】
由概率总和为1可得,由百分位数定义计算80%分位数,由频率分布直方图的频率计算人数,均值判断各选项.
【详解】
由得,A错;
成绩在区间[70,80)的频率为,人数为,B错;
低于90分的频率为,设样本数据的80%分位数约为分,
则,解得,C错;
平均成绩为,D正确.
故选:D.
29.C
【解析】
【分析】
利用百分位数的定义求解即可
【详解】
,因为第6个和第7个数据分别为5.5和6.7,
所以估计这24户居民的月均用水量的第25百分位数为.
故选:C
30.A
【解析】
【分析】
共60个数,计算出第75百分位数是第几个,然后从所给数据中找到.
【详解】
,从表中知第45与46两个数的平均值.
故选:A.
31.BC
【解析】
【分析】
由直方图的面积之和为可判断A选项;求出平均数可判断B选项;求出分位数可判断C选项;计算出该校获得金牌小卫士称号的人数可判断D选项.
【详解】
对于A选项,由频率分布直方图可知,解得,A错;
对于B选项,这组数据的平均数为,B对;
对于C选项,,,
所以,设这组数据分位数为,则,则,解得;
对于D选项,由频率分布直方图可知,该校获得金牌小卫士称号的人数为人,D错.
故选:BC.
32.ACD
【解析】
【分析】
利用频率之和为1可判断选项A,利用频率与频数的关系即可判断选项B,利用频率分布直方图中众数的计算方法求解众数,即可判断选项C,由百分位数的计算方法求解,即可判断选项D.
【详解】
解:由,解得,故选项A正确;
体重不低于60千克的频率为,
所以这100名学生中体重不低于60千克的人数为人,故选项B错误;
100名学生体重的众数约为,故选项C正确;
因为体重不低于60千克的频率为0.3,而体重在,的频率为,
所以计该校学生体重的分位数约为,故选项D正确.
故选:ACD.
33.BD
【解析】
【分析】
根据百分位的概念,即可判定,得到答案.
【详解】
因为为整数,所以第75个数据和第76个数据的平均数为第75百分位数9.3,所以A正确,B不正确;C正确;D不正确.
故选:BD.
34.BCD
【解析】
【分析】
根据频率之和为补全频率分布直方图,由此对选项进行分析,从而确定正确选项.
【详解】
设对应小长方形的高为,
,解得.
所以样本中支出在内的频率为,A选项错误.
,C选项正确.
样本中支出不少于40元的人数为,B选项正确.
该校有2000名学生,则约有人支出在内,D选项正确.
故选:BCD
35.ABC
【解析】
【分析】
由频率分布直方图求得运动时间在分钟的频率,从而得出总人数,再计算后判断各选项.
【详解】
由频率分布直方图得运动时间在分钟的频率是,A正确;
所以总人数为.C正确;
运动时间不少于40分钟的人数为,B正确;
若该校有1000名学生,根据样本频率估计总体频率,只能说明可能有300人放学后体育运动时间在分钟,D错误.
故选:ABC.
36.AB
【解析】
【详解】
根据频率直方图可列下表:
阅读时间/min
抽样人数 10 18 22 25 20 5
抽取的100名学生中有50名为阅读霸,据此可判断该校约有一半学生为阅读霸.
故选:AB.
37.ABD
【解析】
【分析】
根据频率分布直方图,利用频率、频数与样本容量的关系即可解答.
【详解】
由题意可得,调查对象的年龄在[25,30)内的频率为0.03×5=0.15,
∵已知年龄在[25,30)内的调查对象有6人,
∴N=,故A选项正确,
∵年龄在[30,35)内的频率是1-(0.01×2+0.02+0.03×2+0.04)×5=0.3,
∴年龄在[30,35)内的调查对象有40×0.3=12人,故B选项正确,
观察频率分布直方图可知,调查对象中年龄大于35岁的频率(0.04+0.03+0.02+0.01)×5=0.5,故C选项错误,
观察频率分布直方图可知,调查对象中年龄超过45岁的频率(0.01+0.02)×5=0.15,
则调查对象的年龄不超过45岁的频率是1-0.15=0.85,故D选项正确.
故选:ABD.
38.7500
【解析】
【分析】
先求出第五小组的频率,进而根据第一小组、第五小组的频率之比,可求出第一小组的频率,进而可求出第一小组的学生人数.
【详解】
由图可知,第五小组的频率为,
又因为从左至右五个小组的频率之比为5∶7∶12∶10∶6,
所以第一小组、第五小组的频率之比为5∶6,
所以第一小组的频率为.
所以该市6万名高一学生中视力在范围内的学生人数约为.
故答案为:7500
39.616
【解析】
【分析】
计算成绩不低于80的两个小矩形的面积之和,即成绩不低于80的学生的频率,再乘以2200即可.
【详解】
.
故答案为:616.
40.
【解析】
【分析】
根据小矩形的面积之和等于求出区间的小矩形的面积即为该组的频率,再由该频率乘以即可求解.
【详解】
由频率分布直方图可知月工资收入在内的频率为:
,
所以用分层抽样抽出的100人做电话询访,月工资收入在内的频率为,
则月工资收入在内的应抽出人,
故答案为:.
41.0.52
【解析】
【分析】
根据换算方法,及格率与实际及格率的差是内的频率求解.
【详解】
由频率分布直方图,得卷面得分在内的频率为:,
所以按照这种方式求出的及格率与实际及格率的差是0.52.
故答案为:0.52
42.80
【解析】
【分析】
利用百分位数的概念以及频率分布直方图求解..
【详解】
因为前4组数据的频率之和为0.05+0.15+0.2+0.3=0.7,
所以70%分位数为80.
故答案为:80
43.##
【解析】
【分析】
根据题意,结合百分位数的计算方法,即可求解.
【详解】
根据题意,将这40个数据从小到大排列,如下所述,
65,65,66,68,68,69,70,71,72,72,72,73,74,75,76,76,76,77,78,79,
81,82,83,83,84,84,84,85,85,86,87,87,88,89,90,90,90,91,91,92,
由,可知第20百分位数为第8项数据与第9项数据的平均数.
故答案为:.
44.212
【解析】
【分析】
先将数据从小到大排,然后由确定第60百分位数.
【详解】
根据题意,将10个数据从小到大排列:
100,120,125,165,175,190,234,310,425,430;
,
则该组数据的第60百分位数为,
故答案为:212.
45.
【解析】
【分析】
根据百分位数的计算规则计算可得;
【详解】
解:因为,故运动员甲得分的25百分位数为从小到大排列的第3和4个数的平均数,为;
又,所以运动员乙得分的80百分位数为从小到大排列的第10个数,为,所以
故答案为:
46.(1)分;
(2)分;
(3).
【解析】
【分析】
先利用频率之和为,计算出,进而求出平均值即可;
利用百分位数的运算方法,求出成绩的第百分位数;
利用分层抽样取样方法,算出需在分数段内抽人,分别记为,,需在分数段内抽人,分别记为,,,写出样本空间和符合条件样本点数,即可求出相应概率.
(1)
解:由,
得.
数学成绩在:
频率,
频率,
频率,
频率,
频率,
频率,
样本平均值为:,
可以估计样本数据中数学成绩均值为分,
据此可以估计该校高一下学期期中数学考试成绩估计分.
(2)
解:由知样本数据中数学考试成绩在分以下所占比例为,
在分以下所占比例为
因此,第百分位数一定位于内,由,
可以估计样本数据的第百分位数约为分,
据此可以估计该校高一下学期期中数学考试成绩第百分位数约为分.
(3)
解:由题意可知,分数段的人数为 (人),
分数段的人数为 (人).
用按比例分配的分层随机抽样的方法抽取名学生,则需在分数段内抽人,分别记为,,需在分数段内抽人,分别记为,,,
设“从样本中任取人,至少有人在分数段内”为事件,
则样本空间共包含个样本点
而的对立事件包含个样本点
所以,所以,即抽取的这名学生至少有人在内的概率为.
47.(1)8.15,8.5,8.75
(2)7.8g,7.9g.
(3)答案见解析
【解析】
【分析】
(1)将所有数据从小到大排列,由四分位数的定义求解即可;
(2)由,得出产品质量较小的前15%的产品有2个;
(3)先计算95%分位数,再根据25%,50%,95%分位数将珍珠等级进行划分.
(1)
将所有数据从小到大排列,得
7.8,7.9,8.0,8.3,8.4,8.5,8.5,8.5,8.6,8.9,9.0,9.9,
因为共有12个数据,,,,
所以25%分位数是,
50%分位数是,
75%分位数是.
故这组数据的四分位数分别为8.15,8.5,8.75.
(2)
因为共有12个数据,,
所以产品质量较小的前15%的产品有2个,它们的质量分别为7.8g,7.9g.
(3)
由(1)可知样本数据的25%分位数是8.15,50%分位数是8.5
因为,所以95%分位数是第12个数据,即9.9,
所以质量小于等于8.15g的珍珠为次品,质量大于8.15g且小于等于8.5g的珍珠为合格品,质量大于8.5g且小于等于9.9g的珍珠为优等品,质量大于9.9g的珍珠为特优品.
48.(1)频率分布表见解析
(2)频率直方图见解析
(3)频率折线图见解析
(4)19%
【解析】
【分析】
(1)根据所给数据列出频率分布表;
(2)由频率分布表画出频率分布直方图;
(3)由频率分布直方图画出频率分布折线图
(4)由频率分布表可得身高小于134 cm的学生的频率;
(1)
频率分布表如下表所示:
分组 频数 频率
[122,126) 5 0.04 0.01
[126,130) 8 0.07 0.0175
[130,134) 10 0.08 0.02
[134,138) 22 0.18 0.045
[138,142) 33 0.28 0.07
[142,146) 20 0.17 0.0425
[146,150) 11 0.09 0.0225
[150,154) 6 0.05 0.0125
[154,158) 5 0.04 0.01
合计 120 1 0.25
(2)
(3)
(4)
由频率分布表可知身高小于134cm的男孩出现的频率为0.04+0.07+0.08=0.19,所以身高小于134cm的人数约占总人数的19%.
49.(1)785,567,199
(2)a=14, b=17
【解析】
【分析】
(1)根据随机数表的抽样方法抽出数据即可;
(2)由总人数100和数学成绩的优秀率为30%列出方程组,进而解得答案即可.
(1)
根据题意,抽取的数字需在编号001,002,…,800之内,且重复的数字需要剔除,第一个抽取的数字是785,而916,955不满足,接着是567,199,满足题意,即抽取的前3个数字是785,567,199.
(2)
根据题意,,且,
解得:.
50.(1)估计全市居民中月均用水量不低于2.5 t的人数为(万),理由见解析
(2)估计x的值为2.8,理由见解析
【解析】
(1)
由题图可知,不低于2.5 t人数所占百分比为,
所以估计全市居民中月均用水量不低于2.5 t的人数为(万).
(2)
由(1)可知,月均用水量小于2.5 t的居民人数所占百分比为73%,
即73%的居民月均用水量小于2.5 t,
则73%+
所以88%的居民月均用水量小于3 t,故,
所以.
故估计x的值为2.8.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
