人教版数学八年级上册 11.3.2 多边形的内角和 课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级上册 11.3.2 多边形的内角和 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 14:43:56 | ||
图片预览




文档简介
(共21张PPT)
11.3.2 多边形的内角和
11.3 多边形及内角和
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
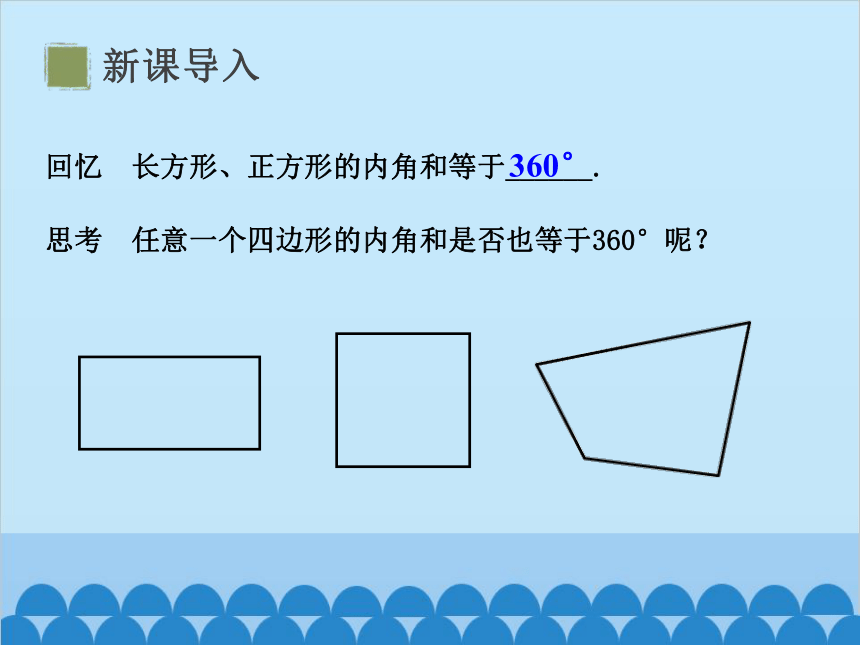
回忆 长方形、正方形的内角和等于______.
360°
思考 任意一个四边形的内角和是否也等于360°呢?
新课导入
讲授新知
贰
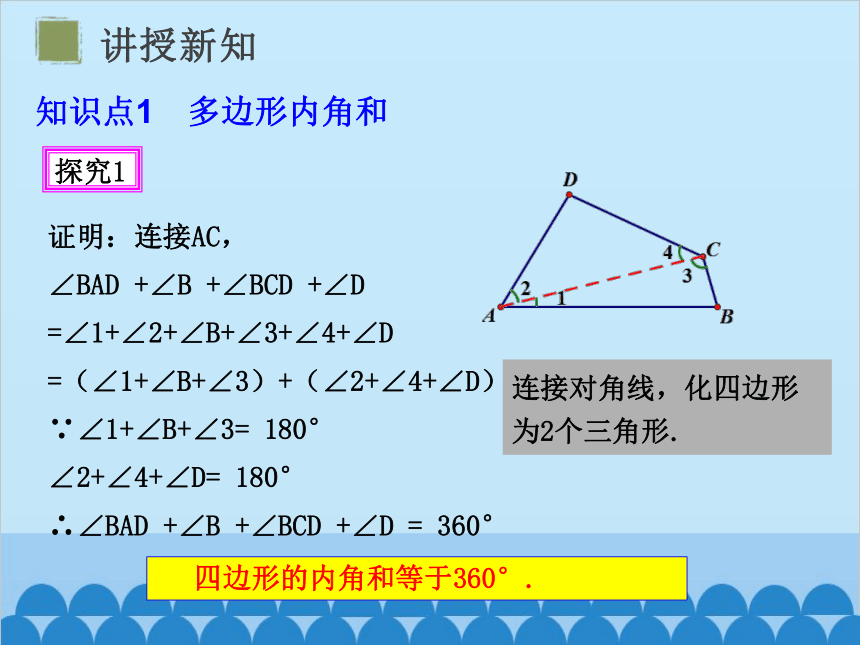
探究1
证明:连接AC,
∠BAD +∠B +∠BCD +∠D
=∠1+∠2+∠B+∠3+∠4+∠D
=(∠1+∠B+∠3)+(∠2+∠4+∠D)
∵∠1+∠B+∠3= 180°
∠2+∠4+∠D= 180°
∴∠BAD +∠B +∠BCD +∠D = 360°
四边形的内角和等于360°.
连接对角线,化四边形为2个三角形.
知识点1 多边形内角和
讲授新知
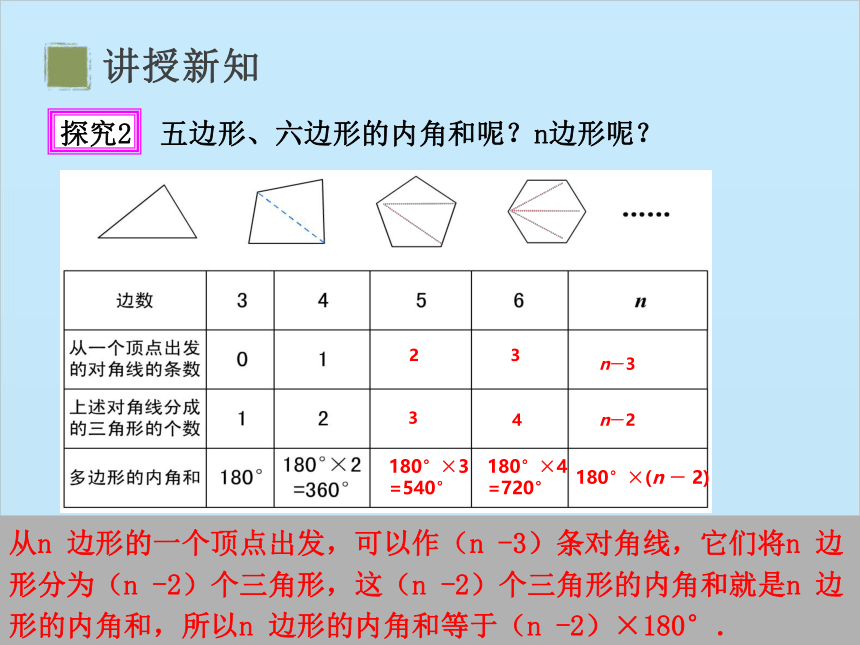
探究2
五边形、六边形的内角和呢?n边形呢?
2
3
180°×3
=540°
3
4
180°×4
=720°
n-3
n-2
180°×(n - 2)
从n 边形的一个顶点出发,可以作(n -3)条对角线,它们将n 边形分为(n -2)个三角形,这(n -2)个三角形的内角和就是n 边形的内角和,所以n 边形的内角和等于(n -2)×180°.
讲授新知
多边形内角和公式为
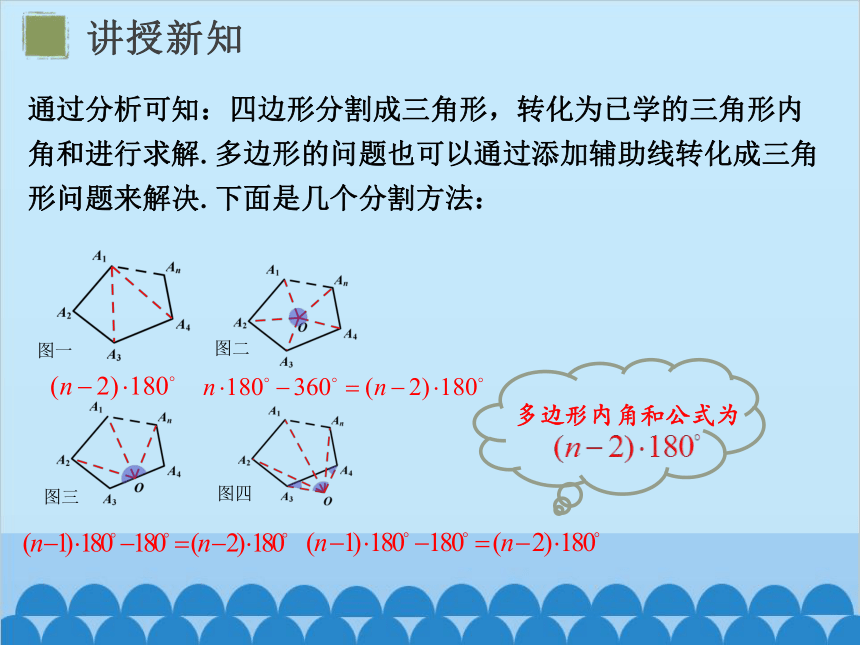
图一
图二
图三
图四
通过分析可知:四边形分割成三角形,转化为已学的三角形内角和进行求解.多边形的问题也可以通过添加辅助线转化成三角形问题来解决.下面是几个分割方法:
讲授新知
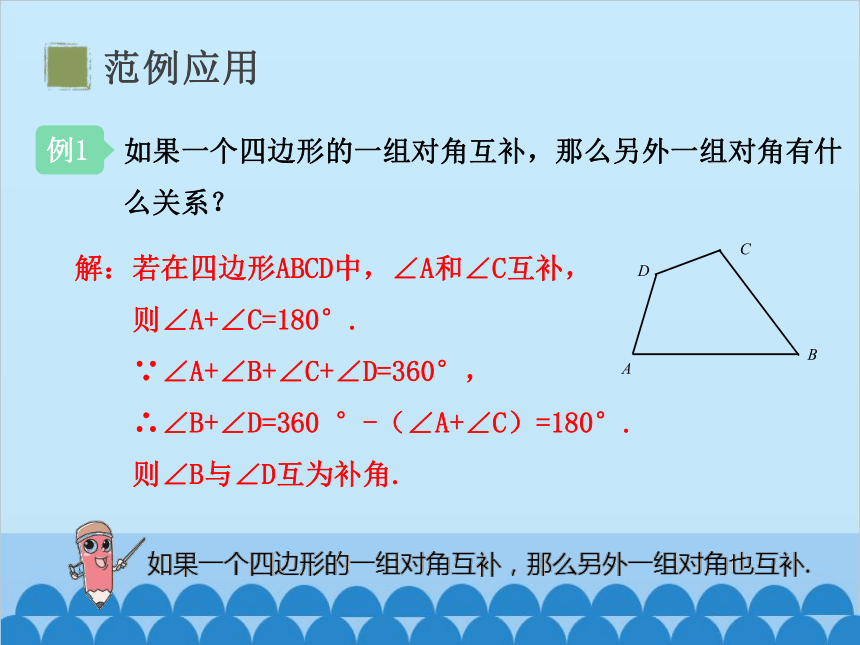
如果一个四边形的一组对角互补,那么另外一组对角有什
么关系?
解:若在四边形ABCD中,∠A和∠C互补,
则∠A+∠C=180°.
∵∠A+∠B+∠C+∠D=360°,
∴∠B+∠D=360 °-(∠A+∠C)=180°.
则∠B与∠D互为补角.
A
C
D
范例应用
例
例1
B
如图所示,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和,六边形的外角和等于多少?
分析:
1.六边形的每一个外角和相邻的内角有什么关系?
2.六边形的6个外角加上与它们相邻的内角,所得总和是多少?
3.上述总和与六边形的内角和、外角和有什么关系?
A
B
C
D
E
F
1
2
3
5
4
6
范例应用
知识点2 多边形的外角和
例2
1.六边形的每一个外角和相邻的内角有什么关系?
2.六边形的6个外角加上与它们相邻的内角,所得总和是多少?
A
B
C
D
E
F
1
2
3
5
4
6
任意一个外角加上与它相邻的内角等于180°.
每一个外角加上与它相邻的内角等于180°,所以六个外角加上与它们相邻的内角等于180°×6=1080°.
范例应用
知识点2 多边形的外角和
3.上述总和与六边形的内角和、外角和有什么关系?
A
B
C
D
E
F
1
2
3
5
4
6
六个外角加上与它们相邻的内角等于180°×6=1080°,
六边形的内角和为180°×4=720°,
六边形的外角和为180°×6-180°×4=360°.
如果是n边形,会得出什么结论呢
范例应用
性质:多边形的外角和等于360°.
n个外角加上与它们相邻的内角等于180°×n,
n边形的内角和为180°×(n-2),
n边形的外角和为180°×n-180°×(n-2)=360°.
知识点2 多边形的外角和
讲授新知
解:设这个多边形为 n 边形,
根据题意,可列方程
( n -2)×180°=3×360°.
解得 n =8.
答:它是八边形.
一个多边形的内角和等于它的外角和的3 倍,它是几边形?
范例应用
当堂训练
叁
1.下列各个度数中,不可能是多边形的内角和的是( )
A.600° B.720° C.900° D.1080°
2.若多边形的边数由 3 增加到 5,则其外角和的度数( )
A.增加 B.减少 C.不变 D.不能确定
3.若一个多边形的每个内角均为150°,则这个多边形的边数为( )
A.9 B.10 C.11 D.12
4. 一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.60° B.72° C.90° D.108
A
C
D
B
当堂训练
5.若n边形的内角和为1440°,则这个n边形的对角线共有________条.
6.一个多边形的各内角都等于120°,它是几边形?
解:设这个多边形的边数为n,
因为各内角都等于120°,所以内角和为120°×n.
由内角和公式,得120° ×n=(n-2)× 180° ,解得n=6.
所以它是六边形.
35
当堂训练
课堂小结
肆
课堂小结
多边形的内角和
(n-2)×180°
(n为≥3的整数)
内角和计算公式
外角和
多边形的外角和等于360°(与边数无关)
正多边形
内角= ,
外角=
课后作业
基础题:1.课后习题 P24第 1,2,3题。
提高题:2.请学有余力的同学P25第 4,5,6,9.10题
谢
谢
11.3.2 多边形的内角和
11.3 多边形及内角和
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
回忆 长方形、正方形的内角和等于______.
360°
思考 任意一个四边形的内角和是否也等于360°呢?
新课导入
讲授新知
贰
探究1
证明:连接AC,
∠BAD +∠B +∠BCD +∠D
=∠1+∠2+∠B+∠3+∠4+∠D
=(∠1+∠B+∠3)+(∠2+∠4+∠D)
∵∠1+∠B+∠3= 180°
∠2+∠4+∠D= 180°
∴∠BAD +∠B +∠BCD +∠D = 360°
四边形的内角和等于360°.
连接对角线,化四边形为2个三角形.
知识点1 多边形内角和
讲授新知
探究2
五边形、六边形的内角和呢?n边形呢?
2
3
180°×3
=540°
3
4
180°×4
=720°
n-3
n-2
180°×(n - 2)
从n 边形的一个顶点出发,可以作(n -3)条对角线,它们将n 边形分为(n -2)个三角形,这(n -2)个三角形的内角和就是n 边形的内角和,所以n 边形的内角和等于(n -2)×180°.
讲授新知
多边形内角和公式为
图一
图二
图三
图四
通过分析可知:四边形分割成三角形,转化为已学的三角形内角和进行求解.多边形的问题也可以通过添加辅助线转化成三角形问题来解决.下面是几个分割方法:
讲授新知
如果一个四边形的一组对角互补,那么另外一组对角有什
么关系?
解:若在四边形ABCD中,∠A和∠C互补,
则∠A+∠C=180°.
∵∠A+∠B+∠C+∠D=360°,
∴∠B+∠D=360 °-(∠A+∠C)=180°.
则∠B与∠D互为补角.
A
C
D
范例应用
例
例1
B
如图所示,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和,六边形的外角和等于多少?
分析:
1.六边形的每一个外角和相邻的内角有什么关系?
2.六边形的6个外角加上与它们相邻的内角,所得总和是多少?
3.上述总和与六边形的内角和、外角和有什么关系?
A
B
C
D
E
F
1
2
3
5
4
6
范例应用
知识点2 多边形的外角和
例2
1.六边形的每一个外角和相邻的内角有什么关系?
2.六边形的6个外角加上与它们相邻的内角,所得总和是多少?
A
B
C
D
E
F
1
2
3
5
4
6
任意一个外角加上与它相邻的内角等于180°.
每一个外角加上与它相邻的内角等于180°,所以六个外角加上与它们相邻的内角等于180°×6=1080°.
范例应用
知识点2 多边形的外角和
3.上述总和与六边形的内角和、外角和有什么关系?
A
B
C
D
E
F
1
2
3
5
4
6
六个外角加上与它们相邻的内角等于180°×6=1080°,
六边形的内角和为180°×4=720°,
六边形的外角和为180°×6-180°×4=360°.
如果是n边形,会得出什么结论呢
范例应用
性质:多边形的外角和等于360°.
n个外角加上与它们相邻的内角等于180°×n,
n边形的内角和为180°×(n-2),
n边形的外角和为180°×n-180°×(n-2)=360°.
知识点2 多边形的外角和
讲授新知
解:设这个多边形为 n 边形,
根据题意,可列方程
( n -2)×180°=3×360°.
解得 n =8.
答:它是八边形.
一个多边形的内角和等于它的外角和的3 倍,它是几边形?
范例应用
当堂训练
叁
1.下列各个度数中,不可能是多边形的内角和的是( )
A.600° B.720° C.900° D.1080°
2.若多边形的边数由 3 增加到 5,则其外角和的度数( )
A.增加 B.减少 C.不变 D.不能确定
3.若一个多边形的每个内角均为150°,则这个多边形的边数为( )
A.9 B.10 C.11 D.12
4. 一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.60° B.72° C.90° D.108
A
C
D
B
当堂训练
5.若n边形的内角和为1440°,则这个n边形的对角线共有________条.
6.一个多边形的各内角都等于120°,它是几边形?
解:设这个多边形的边数为n,
因为各内角都等于120°,所以内角和为120°×n.
由内角和公式,得120° ×n=(n-2)× 180° ,解得n=6.
所以它是六边形.
35
当堂训练
课堂小结
肆
课堂小结
多边形的内角和
(n-2)×180°
(n为≥3的整数)
内角和计算公式
外角和
多边形的外角和等于360°(与边数无关)
正多边形
内角= ,
外角=
课后作业
基础题:1.课后习题 P24第 1,2,3题。
提高题:2.请学有余力的同学P25第 4,5,6,9.10题
谢
谢
