青岛版数学八年级上册 1.2怎样判定三角形全等第1课时 三角形全等的判定(SAS)课件(共18张PPT)
文档属性
| 名称 | 青岛版数学八年级上册 1.2怎样判定三角形全等第1课时 三角形全等的判定(SAS)课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 468.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-20 15:06:05 | ||
图片预览


文档简介
(共18张PPT)
第1章 全等三角形
1.2 怎样判定三角形全等
第1课时 三角形全等的判定(SAS)
复习回顾
1.叙述全等形及全等三角形的概念.
全等三角形的对应边相等,对应角相等.
能够完全重合的两个图形叫做全等形;
能够完全重合的两个三角形,叫做全等三角形.
2.叙述全等三角形的性质.
3.全等三角形的对应边及对应角.
新课导入
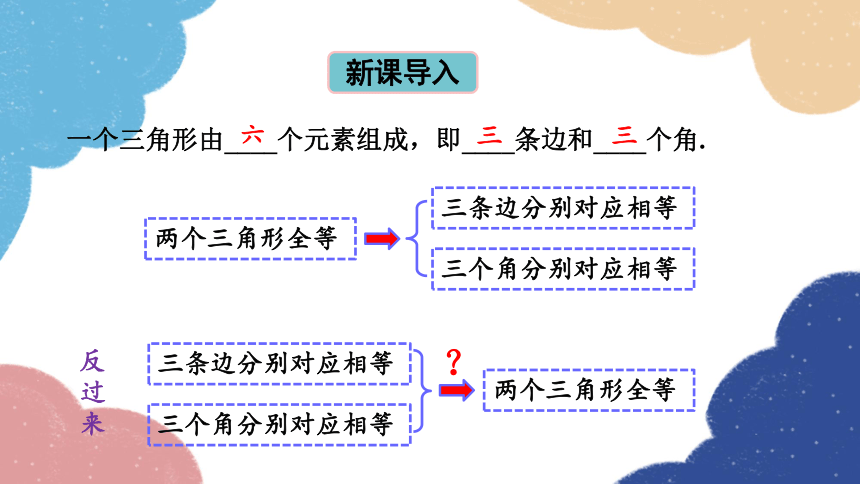
一个三角形由____个元素组成,即____条边和____个角.
六
三
三
两个三角形全等
三条边分别对应相等
三个角分别对应相等
反过来
三条边分别对应相等
三个角分别对应相等
两个三角形全等
?
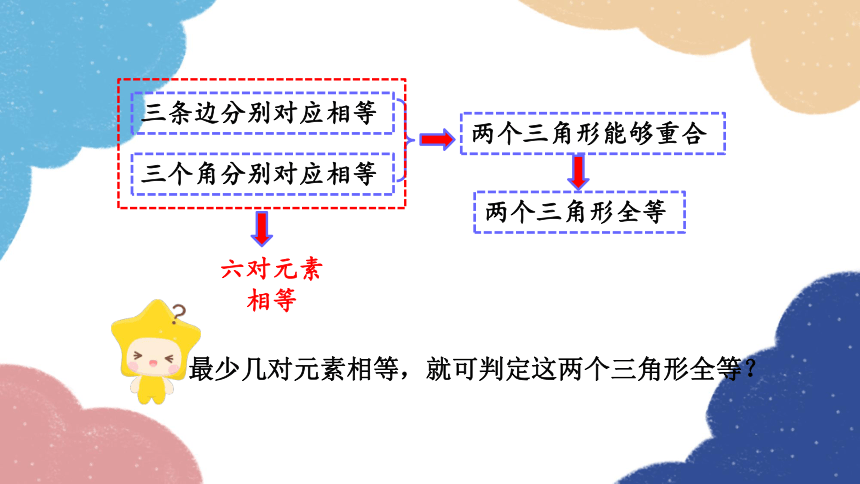
三条边分别对应相等
三个角分别对应相等
两个三角形能够重合
两个三角形全等
最少几对元素相等,就可判定这两个三角形全等?
六对元素相等
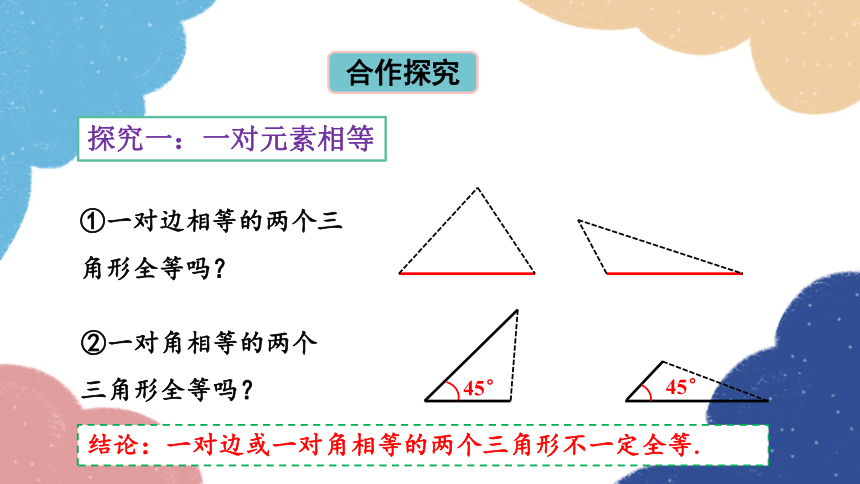
合作探究
①一对边相等的两个三角形全等吗?
探究一:一对元素相等
②一对角相等的两个三角形全等吗?
45°
45°
结论:一对边或一对角相等的两个三角形不一定全等.
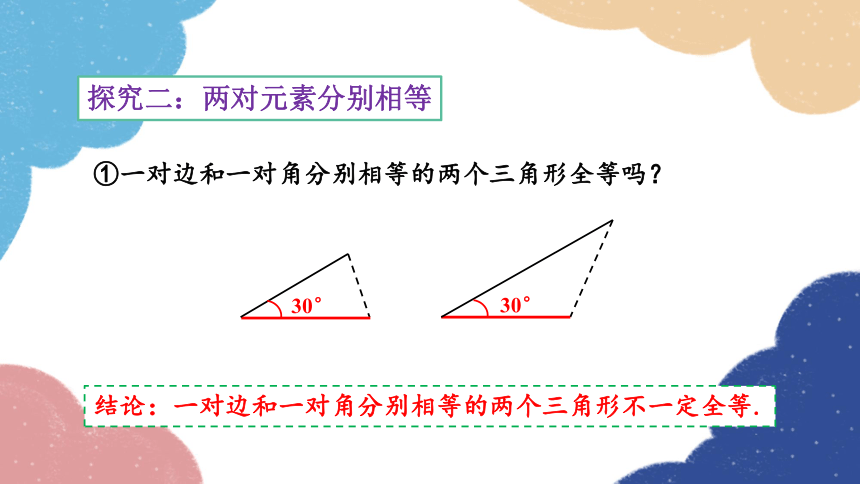
探究二:两对元素分别相等
①一对边和一对角分别相等的两个三角形全等吗?
结论:一对边和一对角分别相等的两个三角形不一定全等.
30°
30°
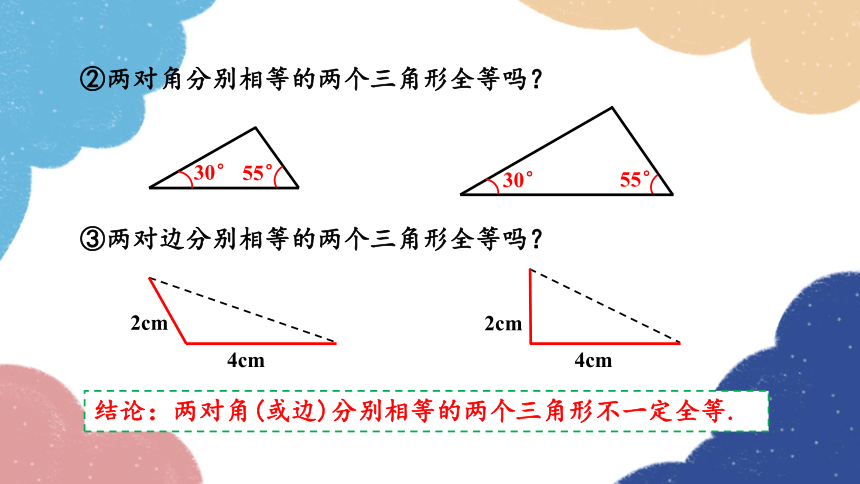
②两对角分别相等的两个三角形全等吗?
30°
55°
55°
30°
③两对边分别相等的两个三角形全等吗?
2cm
4cm
2cm
4cm
结论:两对角(或边)分别相等的两个三角形不一定全等.
归纳总结:
结论:一对或两对元素相等的两个三角形不一定全等.
两个条件
①两对角;
②两对边;
③一对边一对角.
一个条件
①一对角;
②一对边.
探究三:两边及其夹角分别相等
如下图,在△ABC与△A′B′C′中,AB=A′B′,BC=B′C′,如果再添加一个条件∠B=∠B′, △ABC与△A′B′C′全等吗?
A′
B′
C′
A
B
C
A′
B′
C′
A
B
C
如图,把△ABC放到△A′B′C′上,使点B与点B′重合,
因为∠B=∠B′, AB=A′B′,BC=B′C′,
所以点A与点A′重合,点C与点C′重合,
从而△ABC与△A′B′C′全等.
由此,你得出什么结论?
判定方法1 两边及其夹角分别相等的两个三角形全等.
这个判定方法通常简写成“边角边”或“SAS”.
在△ABC与△ A′B′C′中:
符号语言:
因为AB=A′B′,∠B=∠B′,BC= B′C′,
所以△ABC≌△ A′B′C′(SAS).
A′
B′
C′
A
B
C
【例1】如图,已知AB=AD,∠BAC=∠DAC,△ABC与△ADC全等吗?说明你的理由.
解:△ABC与△ADC全等.理由是:
在△ABC与△ADC中,
因为 AB=AD,AC是△ABC与△ADC的公共边,
AC=AC,∠BAC与∠DAC分别是AB与AC,DA与AC的夹角,并且∠BAC=∠DAC,
由SAS,所以 △ABC≌△ADC.
A
B
C
D
【例2】如图,为了测量池塘边上不能直接到达的两点A,B之间的距离,小亮设计了这样一个方案:先在平地上取一个能够直接到达点A与点B的点C,然后在射线AC上取一点D,使CD=CA,在射线BC上取一点E,使CE=CB.测量DE的长,那么DE的长就等于A,B两点之间的距离.他的方案对吗?为什么?
解:他的方案是对的.理由是:
因为CA=CD,CB=CE,∠ACB=∠DCE,由SAS,
所以 △ACB≌△DCE.
因此,DE与AB相等.
课堂小结
1.如果两个三角形的三条边分别相等,三个角分别相等,那么这两个三角形________.
3.三角形全等的判定方法1 两边及其________分别相等的两个三角形全等.
夹角
2.一对元素相等的两个三角形_________全等,两对元素分别相等的两个三角形_________全等.
全等
不一定
不一定
当堂检测
1.如图,AC交BD于点P,AP=DP,则需要“SAS”证明△APB≌△DPC,还需添加的条件是 ( ).
A.BA=CD B.PB=PC
C.∠A=∠D D.∠APB=∠DPC
B
2.如图,根据“SAS”,如果BD=CE,_______=_______,那么即可判定△BDC≌△CEB.
分析:在△BDC和△CEB中,
因为 BD=CE,
∠DBC=∠ECB ,
BC=CB,
所以 △BDC≌△CEB (SAS).
∠DBC
∠ECB
3.如图,已知AB=AC,AE=AD,△ABE与△ACD全等吗?为什么?
解: △ABE与△ACD全等,理由如下:
在△ABE和△ACD中,
因为 AB=AC,
∠A=∠A(公共角),
AE=AD,
所以 △ABE≌△ACD (SAS).
D
C
E
B
A
第1章 全等三角形
1.2 怎样判定三角形全等
第1课时 三角形全等的判定(SAS)
复习回顾
1.叙述全等形及全等三角形的概念.
全等三角形的对应边相等,对应角相等.
能够完全重合的两个图形叫做全等形;
能够完全重合的两个三角形,叫做全等三角形.
2.叙述全等三角形的性质.
3.全等三角形的对应边及对应角.
新课导入
一个三角形由____个元素组成,即____条边和____个角.
六
三
三
两个三角形全等
三条边分别对应相等
三个角分别对应相等
反过来
三条边分别对应相等
三个角分别对应相等
两个三角形全等
?
三条边分别对应相等
三个角分别对应相等
两个三角形能够重合
两个三角形全等
最少几对元素相等,就可判定这两个三角形全等?
六对元素相等
合作探究
①一对边相等的两个三角形全等吗?
探究一:一对元素相等
②一对角相等的两个三角形全等吗?
45°
45°
结论:一对边或一对角相等的两个三角形不一定全等.
探究二:两对元素分别相等
①一对边和一对角分别相等的两个三角形全等吗?
结论:一对边和一对角分别相等的两个三角形不一定全等.
30°
30°
②两对角分别相等的两个三角形全等吗?
30°
55°
55°
30°
③两对边分别相等的两个三角形全等吗?
2cm
4cm
2cm
4cm
结论:两对角(或边)分别相等的两个三角形不一定全等.
归纳总结:
结论:一对或两对元素相等的两个三角形不一定全等.
两个条件
①两对角;
②两对边;
③一对边一对角.
一个条件
①一对角;
②一对边.
探究三:两边及其夹角分别相等
如下图,在△ABC与△A′B′C′中,AB=A′B′,BC=B′C′,如果再添加一个条件∠B=∠B′, △ABC与△A′B′C′全等吗?
A′
B′
C′
A
B
C
A′
B′
C′
A
B
C
如图,把△ABC放到△A′B′C′上,使点B与点B′重合,
因为∠B=∠B′, AB=A′B′,BC=B′C′,
所以点A与点A′重合,点C与点C′重合,
从而△ABC与△A′B′C′全等.
由此,你得出什么结论?
判定方法1 两边及其夹角分别相等的两个三角形全等.
这个判定方法通常简写成“边角边”或“SAS”.
在△ABC与△ A′B′C′中:
符号语言:
因为AB=A′B′,∠B=∠B′,BC= B′C′,
所以△ABC≌△ A′B′C′(SAS).
A′
B′
C′
A
B
C
【例1】如图,已知AB=AD,∠BAC=∠DAC,△ABC与△ADC全等吗?说明你的理由.
解:△ABC与△ADC全等.理由是:
在△ABC与△ADC中,
因为 AB=AD,AC是△ABC与△ADC的公共边,
AC=AC,∠BAC与∠DAC分别是AB与AC,DA与AC的夹角,并且∠BAC=∠DAC,
由SAS,所以 △ABC≌△ADC.
A
B
C
D
【例2】如图,为了测量池塘边上不能直接到达的两点A,B之间的距离,小亮设计了这样一个方案:先在平地上取一个能够直接到达点A与点B的点C,然后在射线AC上取一点D,使CD=CA,在射线BC上取一点E,使CE=CB.测量DE的长,那么DE的长就等于A,B两点之间的距离.他的方案对吗?为什么?
解:他的方案是对的.理由是:
因为CA=CD,CB=CE,∠ACB=∠DCE,由SAS,
所以 △ACB≌△DCE.
因此,DE与AB相等.
课堂小结
1.如果两个三角形的三条边分别相等,三个角分别相等,那么这两个三角形________.
3.三角形全等的判定方法1 两边及其________分别相等的两个三角形全等.
夹角
2.一对元素相等的两个三角形_________全等,两对元素分别相等的两个三角形_________全等.
全等
不一定
不一定
当堂检测
1.如图,AC交BD于点P,AP=DP,则需要“SAS”证明△APB≌△DPC,还需添加的条件是 ( ).
A.BA=CD B.PB=PC
C.∠A=∠D D.∠APB=∠DPC
B
2.如图,根据“SAS”,如果BD=CE,_______=_______,那么即可判定△BDC≌△CEB.
分析:在△BDC和△CEB中,
因为 BD=CE,
∠DBC=∠ECB ,
BC=CB,
所以 △BDC≌△CEB (SAS).
∠DBC
∠ECB
3.如图,已知AB=AC,AE=AD,△ABE与△ACD全等吗?为什么?
解: △ABE与△ACD全等,理由如下:
在△ABE和△ACD中,
因为 AB=AC,
∠A=∠A(公共角),
AE=AD,
所以 △ABE≌△ACD (SAS).
D
C
E
B
A
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
