三角形全等的条件(一)(浙江省台州市)
文档属性
| 名称 | 三角形全等的条件(一)(浙江省台州市) |

|
|
| 格式 | rar | ||
| 文件大小 | 233.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-15 00:00:00 | ||
图片预览



文档简介
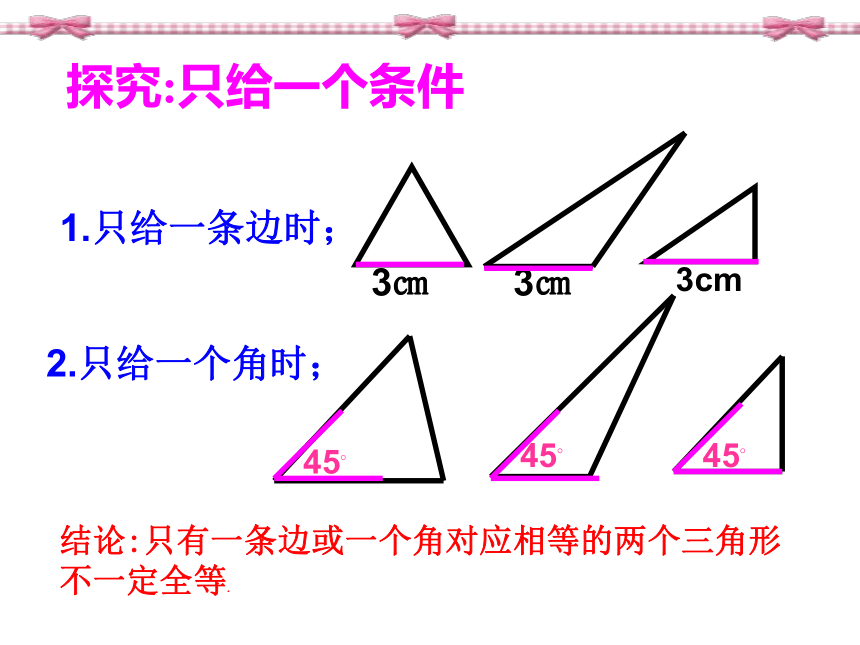
课件16张PPT。§13.2 三角形全等的条件(一)1.只给一条边时;3㎝3㎝探究:只给一个条件45?45?2.只给一个角时;3cm45?结论:只有一条边或一个角对应相等的两个三角形 不一定全等.如果给出两个条件画三角形,
能说出有你哪几种可能的情况?①两角;
②两边;
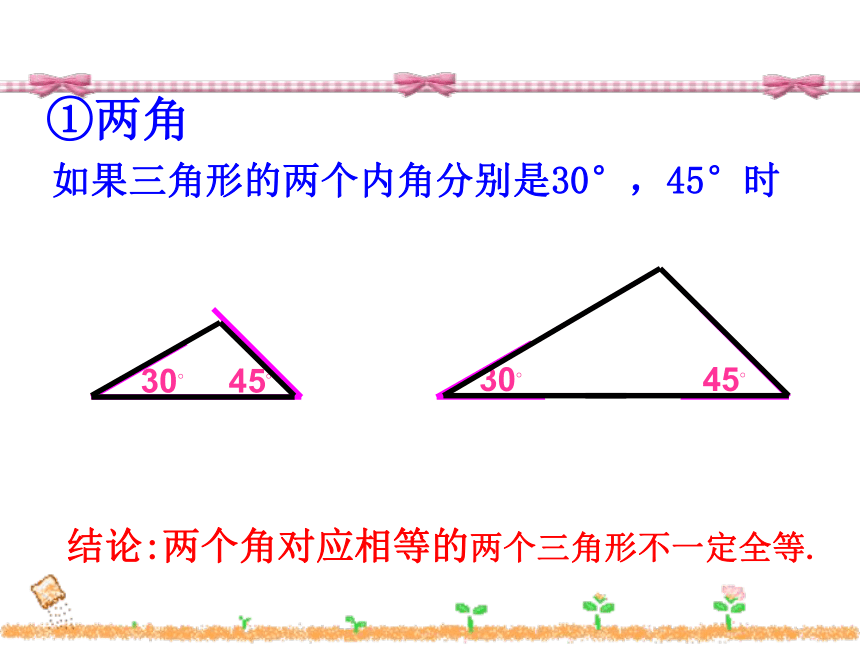
③一边一角。探究:给两个条件如果三角形的两个内角分别是30°,45°时结论:两个角对应相等的两个三角形不一定全等.①两角
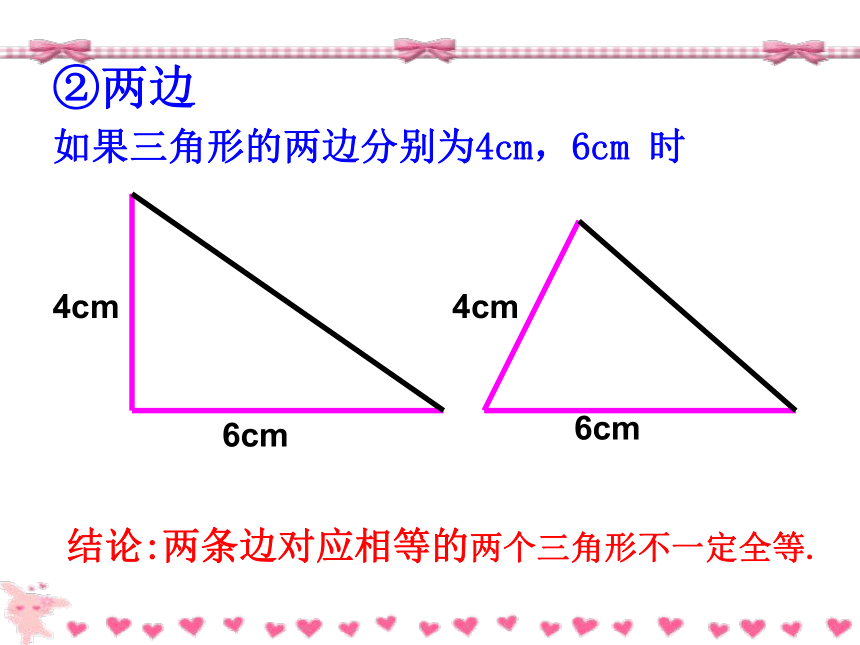
如果三角形的两边分别为4cm,6cm 时6cm6cm4cm4cm结论:两条边对应相等的两个三角形不一定全等.
②两边
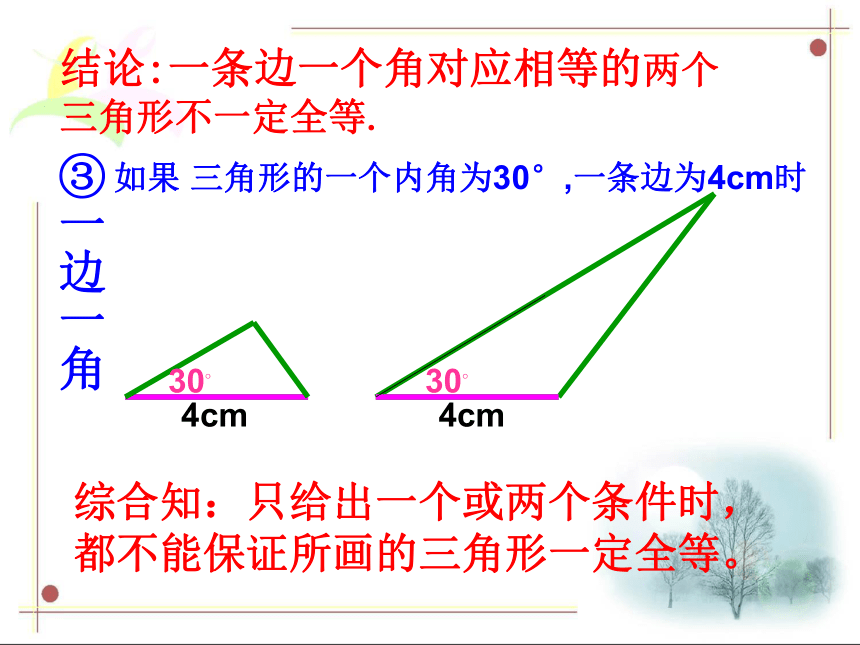
如果 三角形的一个内角为30°,一条边为4cm时4cm4cm30?30?结论:一条边一个角对应相等的两个三角形不一定全等.综合知:只给出一个或两个条件时,都不能保证所画的三角形一定全等。③一边一角如果给出三个条件画三角形,
你能说出有哪几种可能的情况?①三边;
②三角;
③两边一角;
④两角一边。探究:给三个条件
先任意画出一个△ABC,再画一个△ A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA,把画好的△ A′B′C′剪下,放到△ ABC上,你发现了什么?画法:1.画线段B′C′=BC;
2.分别以B′、C′为圆心,线段AB、AC
为半径画弧,两弧相交于点A′;
3.连接A′B′、A′C′.
则△A′B′C′就是所要画的三角形探究: 由此得规律:三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ” 数学符号语言(应用格式)在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)判断两个三角形全等的推理过程,叫做证明三角形全等。这说明,只要三角形的三边确定了,这个三角形的形状和大小就完全确定了,这就是三角形具有稳定性的原因。 解: △ABC≌△DCB
理由如下:
AB = CD
AC = DB
=
SSS △DCBBCCBBF=CD或 BD=CF填空3、如图,AB=AC,BD=CD,BH=CH,图中有 ____ 组全等的三角形.HDCBA三 A C B D证明:∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC(已知)BD=CD(已证)AD=AD(公共边)∴△ABD≌△ACD(SSS)例 如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证: △ABD≌△ACD若要求证:AD⊥BC,你会吗?已知: 如图,A、D、C、F在同一直线上AB=EF,BC=DE,且AD=CF判断下题的证明过程是否有错误的地方,若有在那一步,正确的该怎样写则△ABC与△FED全等证明:在△ABC和△FED中 ⑴AB=EF
BC=DE ⑵
AD=CF∴△ABC≌△FED(SSS) ⑶归纳:①准备条件:证全等时要用的间接条件要先证好;②三角形全等书写三步骤:首先,写出在哪两个三角形中其次,列出三个条件并用大括号括起来最后,写出全等结论并注明理由证明的书写步骤:工人师傅常利用如图所示的仪器平分一个角.AB=AD.BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一射线AE,则AE就是角的平分线.
你能说明其中的道理吗?学以致用已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.ABCD解:在△ACB 和 △ADB中 AC = A D
BC = BD
A B = A B (公共边)∴△ACB≌△ADB(SSS)议一议:连结AB∴∠C=∠D.(全等三角形对应角相等)
能说出有你哪几种可能的情况?①两角;
②两边;
③一边一角。探究:给两个条件如果三角形的两个内角分别是30°,45°时结论:两个角对应相等的两个三角形不一定全等.①两角
如果三角形的两边分别为4cm,6cm 时6cm6cm4cm4cm结论:两条边对应相等的两个三角形不一定全等.
②两边
如果 三角形的一个内角为30°,一条边为4cm时4cm4cm30?30?结论:一条边一个角对应相等的两个三角形不一定全等.综合知:只给出一个或两个条件时,都不能保证所画的三角形一定全等。③一边一角如果给出三个条件画三角形,
你能说出有哪几种可能的情况?①三边;
②三角;
③两边一角;
④两角一边。探究:给三个条件
先任意画出一个△ABC,再画一个△ A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA,把画好的△ A′B′C′剪下,放到△ ABC上,你发现了什么?画法:1.画线段B′C′=BC;
2.分别以B′、C′为圆心,线段AB、AC
为半径画弧,两弧相交于点A′;
3.连接A′B′、A′C′.
则△A′B′C′就是所要画的三角形探究: 由此得规律:三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ” 数学符号语言(应用格式)在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)判断两个三角形全等的推理过程,叫做证明三角形全等。这说明,只要三角形的三边确定了,这个三角形的形状和大小就完全确定了,这就是三角形具有稳定性的原因。 解: △ABC≌△DCB
理由如下:
AB = CD
AC = DB
=
SSS △DCBBCCBBF=CD或 BD=CF填空3、如图,AB=AC,BD=CD,BH=CH,图中有 ____ 组全等的三角形.HDCBA三 A C B D证明:∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC(已知)BD=CD(已证)AD=AD(公共边)∴△ABD≌△ACD(SSS)例 如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证: △ABD≌△ACD若要求证:AD⊥BC,你会吗?已知: 如图,A、D、C、F在同一直线上AB=EF,BC=DE,且AD=CF判断下题的证明过程是否有错误的地方,若有在那一步,正确的该怎样写则△ABC与△FED全等证明:在△ABC和△FED中 ⑴AB=EF
BC=DE ⑵
AD=CF∴△ABC≌△FED(SSS) ⑶归纳:①准备条件:证全等时要用的间接条件要先证好;②三角形全等书写三步骤:首先,写出在哪两个三角形中其次,列出三个条件并用大括号括起来最后,写出全等结论并注明理由证明的书写步骤:工人师傅常利用如图所示的仪器平分一个角.AB=AD.BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一射线AE,则AE就是角的平分线.
你能说明其中的道理吗?学以致用已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.ABCD解:在△ACB 和 △ADB中 AC = A D
BC = BD
A B = A B (公共边)∴△ACB≌△ADB(SSS)议一议:连结AB∴∠C=∠D.(全等三角形对应角相等)
