人教版高中数学必修第二册 第九章 统计 单元测试卷(含解析)
文档属性
| 名称 | 人教版高中数学必修第二册 第九章 统计 单元测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 322.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-19 00:00:00 | ||
图片预览


文档简介
人教版高中数学必修第二册 第九章 统计 单元测试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷60分,第Ⅱ卷90分,共150分,考试时间120分钟.
第Ⅰ卷 (选择题 共60分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.从某地区中小学生中抽取部分学生,进行肺活量调查.经了解,该地区小学、初中、高中三个学段学生的肺活量有较大差异,而同一学段男女生的肺活量差异不大.在下面的抽样方法中,最合理的抽样方法是 ( )
A.抽签法 B.按性别分层随机抽样
C.按学段分层随机抽样 D.随机数法
2.从某小学随机抽取100名学生,将他们的身高(单位:厘米)分布情况汇总如下表:
身高 [100,110) [110,120) [120,130) [130,140) [140,150]
频数 5 35 30 20 10
由此表估计这100名学生身高的中位数为(结果保留4位有效数字) ( )
A.119.3 B.119.7 C.123.3 D.126.7
3.高二(1)班某宿舍有7人,他们的身高(单位:cm)分别为170,168,172,172,175,176,180,则这7个数据的第60百分位数为 ( )
A.168 B.175
C.172 D.176
4.在抽查产品尺寸的过程中,将其尺寸分成若干组,[a,b]是其中的一组.已知该组的频率为m,该组上的频率分布直方图的高为h,则|a-b|等于 ( )
A.mh B. C. D.m+h
5.2020年2月8日,在韩国首尔举行的四大洲花样滑冰锦标赛双人自由滑比赛中,中国组合隋文静、韩聪以总分217.51分拿下四大洲赛冠军,这也是他们第六次获得四大洲冠军.中国另一对组合彭程、金杨以213.29分摘得银牌.花样滑冰锦标赛有9位评委进行评分,首先这9位评委给出某对选手的原始分数,评定该对选手的成绩时从9个原始成绩中去掉一个最高分、一个最低分,得到7个有效评分,7个有效评分与9个原始评分相比,不变的数字特征是 ( )
A.中位数 B.平均数
C.方差 D.极差
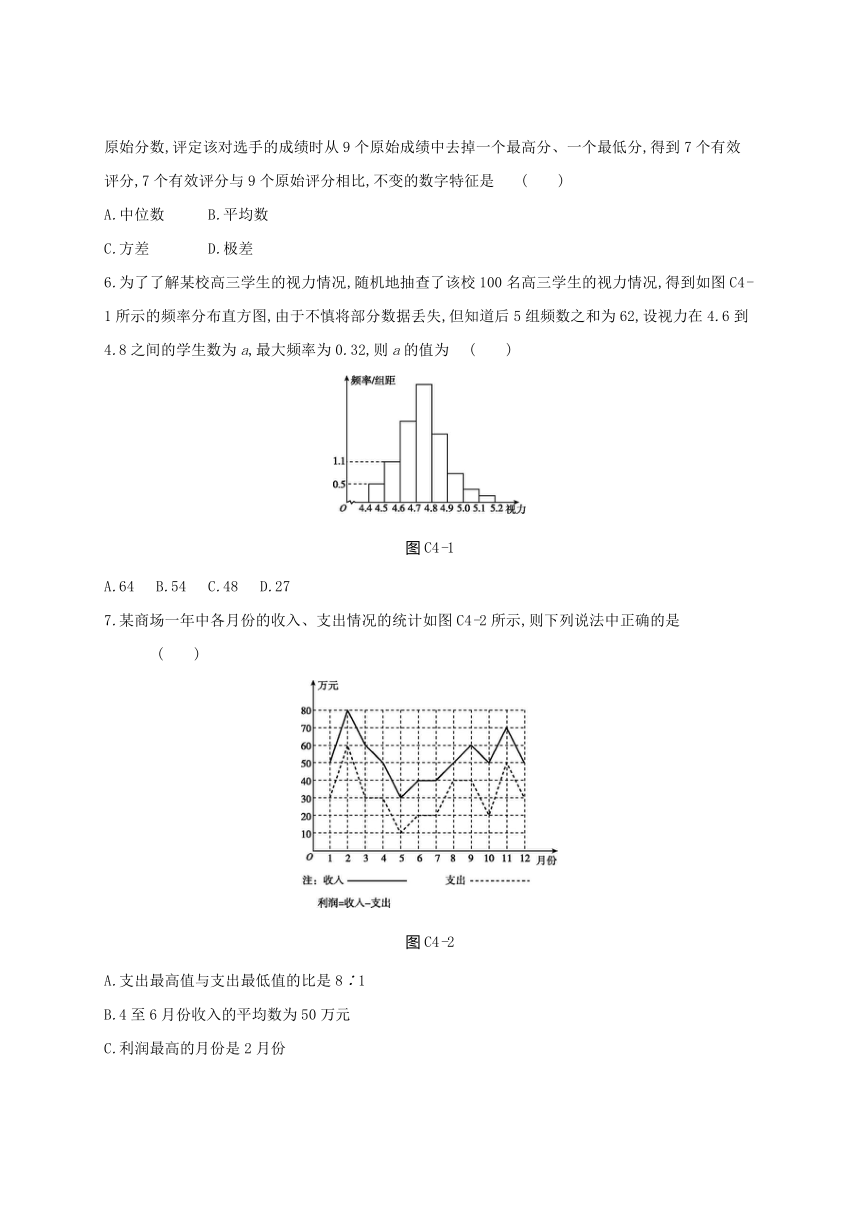
6.为了了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到如图C4-1所示的频率分布直方图,由于不慎将部分数据丢失,但知道后5组频数之和为62,设视力在4.6到4.8之间的学生数为a,最大频率为0.32,则a的值为 ( )
图C4-1
A.64 B.54 C.48 D.27
7.某商场一年中各月份的收入、支出情况的统计如图C4-2所示,则下列说法中正确的是 ( )
图C4-2
A.支出最高值与支出最低值的比是8∶1
B.4至6月份收入的平均数为50万元
C.利润最高的月份是2月份
D.2至3月份的收入的变化率与11至12月份的收入的变化率相同
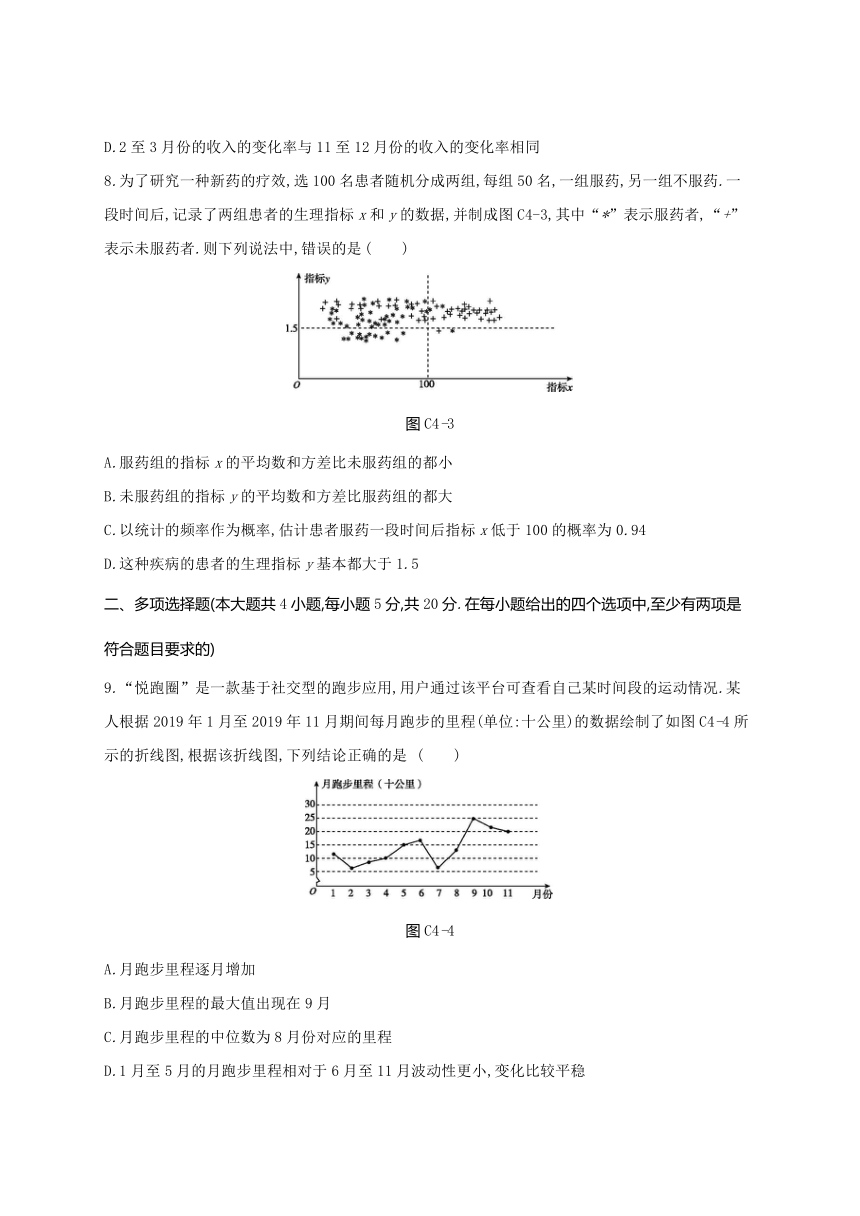
8.为了研究一种新药的疗效,选100名患者随机分成两组,每组50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成图C4-3,其中“*”表示服药者,“+”表示未服药者.则下列说法中,错误的是 ( )
图C4-3
A.服药组的指标x的平均数和方差比未服药组的都小
B.未服药组的指标y的平均数和方差比服药组的都大
C.以统计的频率作为概率,估计患者服药一段时间后指标x低于100的概率为0.94
D.这种疾病的患者的生理指标y基本都大于1.5
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,至少有两项是符合题目要求的)
9.“悦跑圈”是一款基于社交型的跑步应用,用户通过该平台可查看自己某时间段的运动情况.某人根据2019年1月至2019年11月期间每月跑步的里程(单位:十公里)的数据绘制了如图C4-4所示的折线图,根据该折线图,下列结论正确的是 ( )
图C4-4
A.月跑步里程逐月增加
B.月跑步里程的最大值出现在9月
C.月跑步里程的中位数为8月份对应的里程
D.1月至5月的月跑步里程相对于6月至11月波动性更小,变化比较平稳
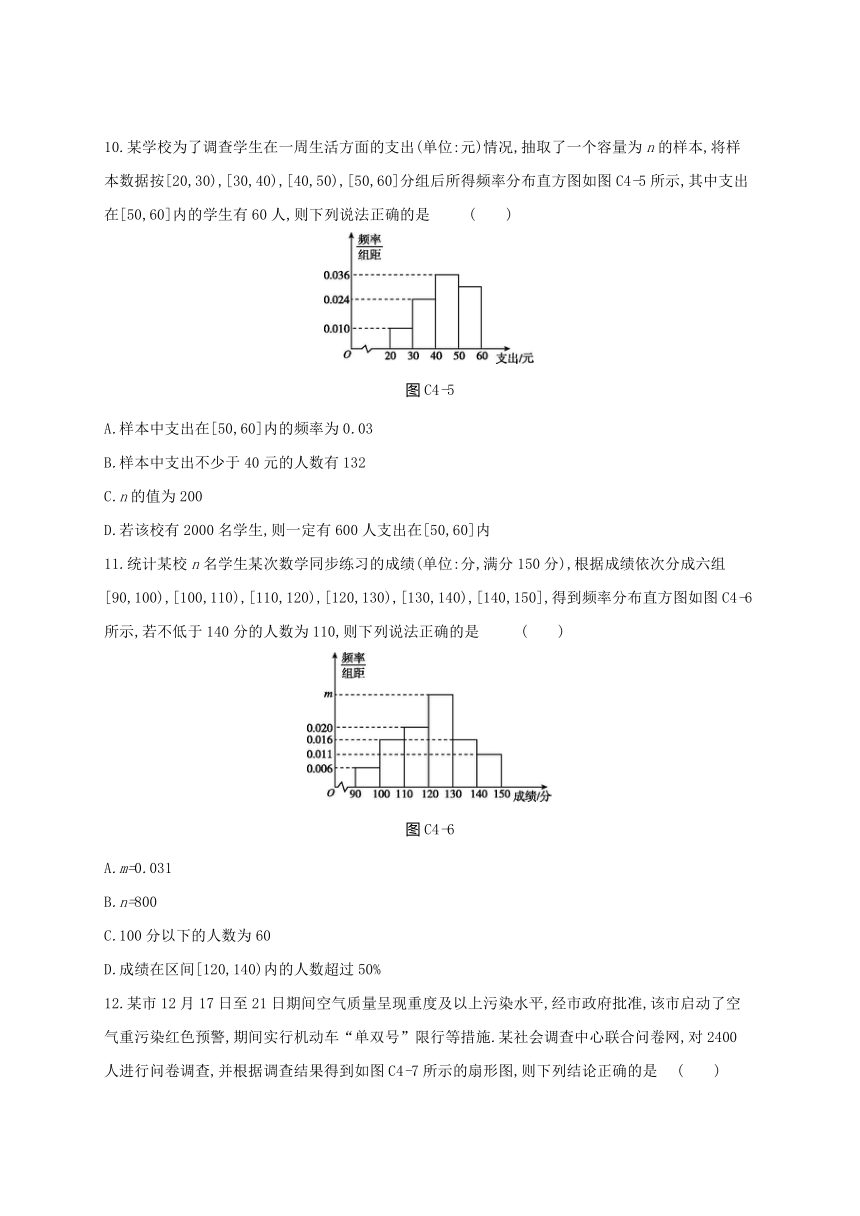
10.某学校为了调查学生在一周生活方面的支出(单位:元)情况,抽取了一个容量为n的样本,将样本数据按[20,30),[30,40),[40,50),[50,60]分组后所得频率分布直方图如图C4-5所示,其中支出在[50,60]内的学生有60人,则下列说法正确的是 ( )
图C4-5
A.样本中支出在[50,60]内的频率为0.03
B.样本中支出不少于40元的人数有132
C.n的值为200
D.若该校有2000名学生,则一定有600人支出在[50,60]内
11.统计某校n名学生某次数学同步练习的成绩(单位:分,满分150分),根据成绩依次分成六组[90,100),[100,110),[110,120),[120,130),[130,140),[140,150],得到频率分布直方图如图C4-6所示,若不低于140分的人数为110,则下列说法正确的是 ( )
图C4-6
A.m=0.031
B.n=800
C.100分以下的人数为60
D.成绩在区间[120,140)内的人数超过50%
12.某市12月17日至21日期间空气质量呈现重度及以上污染水平,经市政府批准,该市启动了空气重污染红色预警,期间实行机动车“单双号”限行等措施.某社会调查中心联合问卷网,对2400人进行问卷调查,并根据调查结果得到如图C4-7所示的扇形图,则下列结论正确的是 ( )
图C4-7
A.“不支持”部分所占的比例是10%
B.“一般”部分对应的人数是800
C.扇形图中如果圆的半径为2,则“非常支持”部分对应扇形的面积是π
D.“支持”部分对应的人数是1080
请将选择题答案填入下表:
题号 1 2 3 4 5 6 7 8 总分
答案
题号 9 10 11 12
答案
第Ⅱ卷 (非选择题 共90分)
三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.一组数据按从小到大的顺序排列为10,12,13,x,17,19,21,24,其中位数为16,则x= .
14.某校为了了解学生收看“空中课堂”的方式,对该校500名学生进行了调查,并把结果绘制成如图C4-8所示的扇形图,那么该校通过手机收看“空中课堂”的学生人数是 .
图C4-8
15.国家禁毒办于2019年11月5日至12月15日在全国青少年毒品预防教育数字化网络平台上开展2019年全国青少年禁毒知识答题活动,活动期间进入答题专区,点击“开始答题”按钮后,系统自动生成20道题.已知某校高二年级有甲、乙、丙、丁、戊五位同学在这次活动中答对的题数分别是17,20,16,18,19,则这五位同学答对题数的方差是 .
16.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图C4-9所示).由图中数据可知a= .若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用比例分配的分层随机抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为 .
图C4-9
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)将一组数据按从小到大的顺序排列,得到-1,0,4,x,7,14,已知这组数据的中位数为5,求这组数据的平均数与方差.
18.(12分)某车站在春运期间为了了解旅客的购票情况,随机调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min).下面是对所得数据进行统计分析后得到的频率分布表和频率分布直方图.
频率 分组 频数
[5,10) 10 0.10
[10,15) 10 ②
[15,20) ① 0.50
[20,25] 30 0.30
合计 100 1.00
解答下列问题:
(1)在表中填写出缺失的数据并补全频率分布直方图(如图C4-10所示);
(2)估计旅客购票用时的平均数.
图C4-10
19.(12分)某班主任利用周末时间对该班2019年最后一次月考的语文作文分数进行了统计,发现分数都位于20~55之间,现将分数情况按[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55]分成七组后,作出频率分布直方图如图C4-11所示,已知m=2n.
(1)求频率分布直方图中m,n的值;
(2)求该班这次月考语文作文分数的平均数和中位数.(每组数据用该组区间的中点值作为代表)
图C4-11
20.(12分)已知甲、乙两人在相同条件下各射靶10次,每次射击的命中环数如图C4-12所示.
(1)求甲、乙两人射击命中环数的平均数和方差;
(2)请根据甲、乙两人射击命中环数的平均数和方差,分析谁的射击水平高.
图C4-12
21.(12分)某地区100位居民的人均月用水量(单位:t)的分组及各组的频数分别为 [0,0.5],4;(0.5,1],8;(1,1.5],15;(1.5,2],22;(2,2.5],25;(2.5,3],14;(3,3.5],6;(3.5,4],4;(4,4.5],2.
(1)列出样本的频率分布表.
(2)画出频率分布直方图,并根据直方图估计这组数据的平均数、中位数、众数.
(3)当地政府制定了人均月用水量不超过3 t的标准,若超过3 t则加倍收费,当地政府说,85%以上的居民不超过这个标准,这个解释对吗 为什么
22.(12分)我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了某年100户家庭的月均用水量(单位:t),将数据按照[0,2),[2,4),[4,6),[6,8),[8,10]分成5组,制成了如图C4-13所示的频率分布直方图.
(1)假设同组中的每个数据都用该组区间的中点值代替,求全市家庭月均用水量平均数的估计值(精确到0.01);
(2)求全市家庭月均用水量的25%分位数的估计值(精确到0.01).
图C4-13
参考答案与解析
1.C [解析] 由题意得,最合理的抽样方法是按学段分层随机抽样,故选C.
2.C [解析] 设中位数为t,则有++×=0.5,解得t≈123.3.故选C.
3.B [解析] 将这7人的身高从小到大排序,可得168,170,172,172,175,176,180.∵7×60%=4.2,∴第5个数据为所求的第60百分位数,即这7个数据的第60百分位数为175.故选B.
4.C [解析] 在频率分布直方图中小长方形的高等于,所以h=,则|a-b|=,故选C.
5.A [解析] 根据题意可知,不变的数字特征是中位数.故选A.
6.B [解析] 前两组的频数为100×(0.05+0.11)=16.因为后五组的频数之和为62,所以前三组的频数之和为38,所以第三组的频数为38-16=22.又最大频率为0.32,故第四组的频数为0.32×100=32.所以a=22+32=54.故选B.
7.D [解析] 由图可知,支出最高值为60万元,支出最低值为10万元,其比是6∶1,故A错误;4至6月份的平均收入为×(50+30+40)=40(万元),故B错误;利润最高的月份为3月份和10月份,故C错误;由图可知2至3月份的收入的变化率与11至12月份的收入的变化率相同,故D正确.故选D.
8.B [解析] 服药组的指标x的取值相对集中,方差较小,且服药组的指标x的平均数小于未服药组的指标x的平均数,故选项A中说法正确;未服药组的指标y的取值相对集中,方差较小,故选项B中说法错误;服药组的指标x值有3个大于100,所以估计患者服药一段时间后指标x低于100的概率为0.94,故选项C中说法正确;未服药组的指标y值只有1个数据比1.5小,则这种疾病的患者的生理指标y基本都大于1.5,故选项D中说法正确.故选B.
9.BCD [解析] 2月跑步里程比1月的小,故A错误;月跑步里程9月最大,故B正确;月跑步里程从小到大对应的月份依次为2月、7月、3月、4月、1月、8月、5月、6月、11月、10月、9月,故月跑步里程的中位数为8月份对应的里程,故C正确;1月至5月的月跑步里程相对于6月至11月,波动性更小,变化比较平稳,故D正确.故选BCD.
10.BC [解析] 由频率分布直方图得,样本中支出在[50,60]内的频率为1-(0.01+0.024+0.036)×10=0.3,故A错误;样本中支出不少于40元的人数为×60+60=132,故B正确;n==200,故C正确;在D中,若该校有2000名学生,则大约有600人支出在[50,60]内,故D错误.故选BC.
11.AC [解析] 由图可知10×(m+0.020+0.016+0.016+0.011+0.006)=1,解得m=0.031,故A正确;因为不低于140分的频率为0.011×10=0.11,所以n==1000,故B错误;因为100分以下的频率为0.006×10=0.06,所以100分以下的人数为1000×0.06=60,故C正确;对选项D,成绩在区间[120,140)内的频率为0.031×10+0.016×10=0.47<0.5,人数不超过50%,故D错误.故选AC.
12.ACD [解析] “不支持”部分所占的比例是1-45%-30%-15%=10%,A正确;“一般”部分对应的人数是2400×15%=360,B不正确;“非常支持”部分对应扇形的面积是π×22×30%=π,C正确;“支持”部分对应的人数为2400×45%=1080,D正确.故选ACD.
13.15 [解析] 由中位数的定义知=16,∴x=15.
14.25 [解析] ∵该校通过手机收看“空中课堂”的学生人数所占的百分比为1-(25%+70%)=5%,∴该校通过手机收看“空中课堂”的学生人数是500×5%=25.
15.2 [解析] 这五位同学答对题数的平均数==18,则方差s2=×[(17-18)2+(20-18)2+(16-18)2+(18-18)2+(19-18)2]=2.
16.0.030 3 [解析] 因为10×(0.035+0.020+0.010+0.005+a)=1,所以a=0.030.身高在[120,130),[130,140),[140,150]三组内的学生人数为100×(0.030+0.020+0.010)×10=60,其中身高在[140,150]内的学生中人数为100×0.010×10=10,所以从身高在[140,150]内的学生中选取的人数应为×18=3.
17.解:因为数据-1,0,4,x,7,14的中位数为5,所以=5,解得x=6.
设这组数据的平均数为,方差为s2,则=×(-1+0+4+6+7+14)=5,
s2=×[(-1-5)2+(0-5)2+(4-5)2+(6-5)2+(7-5)2+(14-5)2]=.
18.解:(1)表中缺失的数据分别为①50,②0.10.
补全后的频率分布直方图如图所示.
(2)估计旅客购票用时的平均数为7.5×0.10+12.5×0.10+17.5×0.50+22.5×0.30=17.5(min).
19.解:(1)由频率分布直方图,得
解得
(2)该班这次月考语文作文分数的平均数为22.5×0.05+27.5×0.15+32.5×0.3+37.5×0.2+42.5×0.15+47.5×0.1+52.5×0.05=36.25.
因为(0.01+0.03+0.06)×5=0.5,所以该班这次月考语文作文分数的中位数为35.
20.解:(1)由折线图可知甲射击10次命中的环数分别为9,5,7,8,7,6,8,6,7,7.乙射击10次命中的环数分别为2,4,6,8,7,7,8,9,9,10.
则=×(9+5+7+8+7+6+8+6+7+7)=7(环).
=×(2+4+6+8+7+7+8+9+9+10)=7(环),
=×[(9-7)2+(5-7)2+(7-7)2×4+(6-7)2×2+(8-7)2×2]=1.2,
=×[(2-7)2+(4-7)2+(6-7)2+(7-7)2×2+(8-7)2×2+(9-7)2×2+(10-7)2]=5.4.
(2)因为=,<,
所以甲的射击稳定性比乙好,故甲的射击水平高.
21.解:(1)作出频数分布表,如下.
分组 频数 频率
[0,0.5] 4 0.04
(0.5,1] 8 0.08
(1,1.5] 15 0.15
(1.5,2] 22 0.22
(2,2.5] 25 0.25
(2.5,3] 14 0.14
(3,3.5] 6 0.06
(3.5,4] 4 0.04
(4,4.5] 2 0.02
合计 100 1.00
(2)由频率分布表画出频率分布直方图,如图所示.
由频率分布直方图得这组数据的平均数=0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25×0.06+3.75×0.04+4.25×0.02=2.02.
∵人均月用水量在[0,2]内的频率为0.04+0.08+0.15+0.22=0.49,
在(2,2.5]内的频率为0.25,∴中位数为2+×0.5=2.02.
众数为=2.25.
(3)月用水量在3 t以上的居民的比例为6%+4%+2%=12%,
即大约有12%的居民月用水量在3 t以上,88%的居民月用水量不超过3 t,因此政府的解释是正确的.
22.解:(1)因为0.06×2×1+0.11×2×3+0.18×2×5+0.09×2×7+0.06×2×9=4.92.
因此全市家庭月均用水量平均数的估计值为4.92 t.
(2)频率分布直方图中,用水量低于2 t的频率为0.06×2=0.12.
用水量低于4 t的频率为0.06×2+0.11×2=0.34.
故全市家庭月均用水量的25%分位数的估计值为2+≈3.18(t).
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷60分,第Ⅱ卷90分,共150分,考试时间120分钟.
第Ⅰ卷 (选择题 共60分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.从某地区中小学生中抽取部分学生,进行肺活量调查.经了解,该地区小学、初中、高中三个学段学生的肺活量有较大差异,而同一学段男女生的肺活量差异不大.在下面的抽样方法中,最合理的抽样方法是 ( )
A.抽签法 B.按性别分层随机抽样
C.按学段分层随机抽样 D.随机数法
2.从某小学随机抽取100名学生,将他们的身高(单位:厘米)分布情况汇总如下表:
身高 [100,110) [110,120) [120,130) [130,140) [140,150]
频数 5 35 30 20 10
由此表估计这100名学生身高的中位数为(结果保留4位有效数字) ( )
A.119.3 B.119.7 C.123.3 D.126.7
3.高二(1)班某宿舍有7人,他们的身高(单位:cm)分别为170,168,172,172,175,176,180,则这7个数据的第60百分位数为 ( )
A.168 B.175
C.172 D.176
4.在抽查产品尺寸的过程中,将其尺寸分成若干组,[a,b]是其中的一组.已知该组的频率为m,该组上的频率分布直方图的高为h,则|a-b|等于 ( )
A.mh B. C. D.m+h
5.2020年2月8日,在韩国首尔举行的四大洲花样滑冰锦标赛双人自由滑比赛中,中国组合隋文静、韩聪以总分217.51分拿下四大洲赛冠军,这也是他们第六次获得四大洲冠军.中国另一对组合彭程、金杨以213.29分摘得银牌.花样滑冰锦标赛有9位评委进行评分,首先这9位评委给出某对选手的原始分数,评定该对选手的成绩时从9个原始成绩中去掉一个最高分、一个最低分,得到7个有效评分,7个有效评分与9个原始评分相比,不变的数字特征是 ( )
A.中位数 B.平均数
C.方差 D.极差
6.为了了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到如图C4-1所示的频率分布直方图,由于不慎将部分数据丢失,但知道后5组频数之和为62,设视力在4.6到4.8之间的学生数为a,最大频率为0.32,则a的值为 ( )
图C4-1
A.64 B.54 C.48 D.27
7.某商场一年中各月份的收入、支出情况的统计如图C4-2所示,则下列说法中正确的是 ( )
图C4-2
A.支出最高值与支出最低值的比是8∶1
B.4至6月份收入的平均数为50万元
C.利润最高的月份是2月份
D.2至3月份的收入的变化率与11至12月份的收入的变化率相同
8.为了研究一种新药的疗效,选100名患者随机分成两组,每组50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成图C4-3,其中“*”表示服药者,“+”表示未服药者.则下列说法中,错误的是 ( )
图C4-3
A.服药组的指标x的平均数和方差比未服药组的都小
B.未服药组的指标y的平均数和方差比服药组的都大
C.以统计的频率作为概率,估计患者服药一段时间后指标x低于100的概率为0.94
D.这种疾病的患者的生理指标y基本都大于1.5
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,至少有两项是符合题目要求的)
9.“悦跑圈”是一款基于社交型的跑步应用,用户通过该平台可查看自己某时间段的运动情况.某人根据2019年1月至2019年11月期间每月跑步的里程(单位:十公里)的数据绘制了如图C4-4所示的折线图,根据该折线图,下列结论正确的是 ( )
图C4-4
A.月跑步里程逐月增加
B.月跑步里程的最大值出现在9月
C.月跑步里程的中位数为8月份对应的里程
D.1月至5月的月跑步里程相对于6月至11月波动性更小,变化比较平稳
10.某学校为了调查学生在一周生活方面的支出(单位:元)情况,抽取了一个容量为n的样本,将样本数据按[20,30),[30,40),[40,50),[50,60]分组后所得频率分布直方图如图C4-5所示,其中支出在[50,60]内的学生有60人,则下列说法正确的是 ( )
图C4-5
A.样本中支出在[50,60]内的频率为0.03
B.样本中支出不少于40元的人数有132
C.n的值为200
D.若该校有2000名学生,则一定有600人支出在[50,60]内
11.统计某校n名学生某次数学同步练习的成绩(单位:分,满分150分),根据成绩依次分成六组[90,100),[100,110),[110,120),[120,130),[130,140),[140,150],得到频率分布直方图如图C4-6所示,若不低于140分的人数为110,则下列说法正确的是 ( )
图C4-6
A.m=0.031
B.n=800
C.100分以下的人数为60
D.成绩在区间[120,140)内的人数超过50%
12.某市12月17日至21日期间空气质量呈现重度及以上污染水平,经市政府批准,该市启动了空气重污染红色预警,期间实行机动车“单双号”限行等措施.某社会调查中心联合问卷网,对2400人进行问卷调查,并根据调查结果得到如图C4-7所示的扇形图,则下列结论正确的是 ( )
图C4-7
A.“不支持”部分所占的比例是10%
B.“一般”部分对应的人数是800
C.扇形图中如果圆的半径为2,则“非常支持”部分对应扇形的面积是π
D.“支持”部分对应的人数是1080
请将选择题答案填入下表:
题号 1 2 3 4 5 6 7 8 总分
答案
题号 9 10 11 12
答案
第Ⅱ卷 (非选择题 共90分)
三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.一组数据按从小到大的顺序排列为10,12,13,x,17,19,21,24,其中位数为16,则x= .
14.某校为了了解学生收看“空中课堂”的方式,对该校500名学生进行了调查,并把结果绘制成如图C4-8所示的扇形图,那么该校通过手机收看“空中课堂”的学生人数是 .
图C4-8
15.国家禁毒办于2019年11月5日至12月15日在全国青少年毒品预防教育数字化网络平台上开展2019年全国青少年禁毒知识答题活动,活动期间进入答题专区,点击“开始答题”按钮后,系统自动生成20道题.已知某校高二年级有甲、乙、丙、丁、戊五位同学在这次活动中答对的题数分别是17,20,16,18,19,则这五位同学答对题数的方差是 .
16.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图C4-9所示).由图中数据可知a= .若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用比例分配的分层随机抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为 .
图C4-9
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)将一组数据按从小到大的顺序排列,得到-1,0,4,x,7,14,已知这组数据的中位数为5,求这组数据的平均数与方差.
18.(12分)某车站在春运期间为了了解旅客的购票情况,随机调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min).下面是对所得数据进行统计分析后得到的频率分布表和频率分布直方图.
频率 分组 频数
[5,10) 10 0.10
[10,15) 10 ②
[15,20) ① 0.50
[20,25] 30 0.30
合计 100 1.00
解答下列问题:
(1)在表中填写出缺失的数据并补全频率分布直方图(如图C4-10所示);
(2)估计旅客购票用时的平均数.
图C4-10
19.(12分)某班主任利用周末时间对该班2019年最后一次月考的语文作文分数进行了统计,发现分数都位于20~55之间,现将分数情况按[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55]分成七组后,作出频率分布直方图如图C4-11所示,已知m=2n.
(1)求频率分布直方图中m,n的值;
(2)求该班这次月考语文作文分数的平均数和中位数.(每组数据用该组区间的中点值作为代表)
图C4-11
20.(12分)已知甲、乙两人在相同条件下各射靶10次,每次射击的命中环数如图C4-12所示.
(1)求甲、乙两人射击命中环数的平均数和方差;
(2)请根据甲、乙两人射击命中环数的平均数和方差,分析谁的射击水平高.
图C4-12
21.(12分)某地区100位居民的人均月用水量(单位:t)的分组及各组的频数分别为 [0,0.5],4;(0.5,1],8;(1,1.5],15;(1.5,2],22;(2,2.5],25;(2.5,3],14;(3,3.5],6;(3.5,4],4;(4,4.5],2.
(1)列出样本的频率分布表.
(2)画出频率分布直方图,并根据直方图估计这组数据的平均数、中位数、众数.
(3)当地政府制定了人均月用水量不超过3 t的标准,若超过3 t则加倍收费,当地政府说,85%以上的居民不超过这个标准,这个解释对吗 为什么
22.(12分)我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了某年100户家庭的月均用水量(单位:t),将数据按照[0,2),[2,4),[4,6),[6,8),[8,10]分成5组,制成了如图C4-13所示的频率分布直方图.
(1)假设同组中的每个数据都用该组区间的中点值代替,求全市家庭月均用水量平均数的估计值(精确到0.01);
(2)求全市家庭月均用水量的25%分位数的估计值(精确到0.01).
图C4-13
参考答案与解析
1.C [解析] 由题意得,最合理的抽样方法是按学段分层随机抽样,故选C.
2.C [解析] 设中位数为t,则有++×=0.5,解得t≈123.3.故选C.
3.B [解析] 将这7人的身高从小到大排序,可得168,170,172,172,175,176,180.∵7×60%=4.2,∴第5个数据为所求的第60百分位数,即这7个数据的第60百分位数为175.故选B.
4.C [解析] 在频率分布直方图中小长方形的高等于,所以h=,则|a-b|=,故选C.
5.A [解析] 根据题意可知,不变的数字特征是中位数.故选A.
6.B [解析] 前两组的频数为100×(0.05+0.11)=16.因为后五组的频数之和为62,所以前三组的频数之和为38,所以第三组的频数为38-16=22.又最大频率为0.32,故第四组的频数为0.32×100=32.所以a=22+32=54.故选B.
7.D [解析] 由图可知,支出最高值为60万元,支出最低值为10万元,其比是6∶1,故A错误;4至6月份的平均收入为×(50+30+40)=40(万元),故B错误;利润最高的月份为3月份和10月份,故C错误;由图可知2至3月份的收入的变化率与11至12月份的收入的变化率相同,故D正确.故选D.
8.B [解析] 服药组的指标x的取值相对集中,方差较小,且服药组的指标x的平均数小于未服药组的指标x的平均数,故选项A中说法正确;未服药组的指标y的取值相对集中,方差较小,故选项B中说法错误;服药组的指标x值有3个大于100,所以估计患者服药一段时间后指标x低于100的概率为0.94,故选项C中说法正确;未服药组的指标y值只有1个数据比1.5小,则这种疾病的患者的生理指标y基本都大于1.5,故选项D中说法正确.故选B.
9.BCD [解析] 2月跑步里程比1月的小,故A错误;月跑步里程9月最大,故B正确;月跑步里程从小到大对应的月份依次为2月、7月、3月、4月、1月、8月、5月、6月、11月、10月、9月,故月跑步里程的中位数为8月份对应的里程,故C正确;1月至5月的月跑步里程相对于6月至11月,波动性更小,变化比较平稳,故D正确.故选BCD.
10.BC [解析] 由频率分布直方图得,样本中支出在[50,60]内的频率为1-(0.01+0.024+0.036)×10=0.3,故A错误;样本中支出不少于40元的人数为×60+60=132,故B正确;n==200,故C正确;在D中,若该校有2000名学生,则大约有600人支出在[50,60]内,故D错误.故选BC.
11.AC [解析] 由图可知10×(m+0.020+0.016+0.016+0.011+0.006)=1,解得m=0.031,故A正确;因为不低于140分的频率为0.011×10=0.11,所以n==1000,故B错误;因为100分以下的频率为0.006×10=0.06,所以100分以下的人数为1000×0.06=60,故C正确;对选项D,成绩在区间[120,140)内的频率为0.031×10+0.016×10=0.47<0.5,人数不超过50%,故D错误.故选AC.
12.ACD [解析] “不支持”部分所占的比例是1-45%-30%-15%=10%,A正确;“一般”部分对应的人数是2400×15%=360,B不正确;“非常支持”部分对应扇形的面积是π×22×30%=π,C正确;“支持”部分对应的人数为2400×45%=1080,D正确.故选ACD.
13.15 [解析] 由中位数的定义知=16,∴x=15.
14.25 [解析] ∵该校通过手机收看“空中课堂”的学生人数所占的百分比为1-(25%+70%)=5%,∴该校通过手机收看“空中课堂”的学生人数是500×5%=25.
15.2 [解析] 这五位同学答对题数的平均数==18,则方差s2=×[(17-18)2+(20-18)2+(16-18)2+(18-18)2+(19-18)2]=2.
16.0.030 3 [解析] 因为10×(0.035+0.020+0.010+0.005+a)=1,所以a=0.030.身高在[120,130),[130,140),[140,150]三组内的学生人数为100×(0.030+0.020+0.010)×10=60,其中身高在[140,150]内的学生中人数为100×0.010×10=10,所以从身高在[140,150]内的学生中选取的人数应为×18=3.
17.解:因为数据-1,0,4,x,7,14的中位数为5,所以=5,解得x=6.
设这组数据的平均数为,方差为s2,则=×(-1+0+4+6+7+14)=5,
s2=×[(-1-5)2+(0-5)2+(4-5)2+(6-5)2+(7-5)2+(14-5)2]=.
18.解:(1)表中缺失的数据分别为①50,②0.10.
补全后的频率分布直方图如图所示.
(2)估计旅客购票用时的平均数为7.5×0.10+12.5×0.10+17.5×0.50+22.5×0.30=17.5(min).
19.解:(1)由频率分布直方图,得
解得
(2)该班这次月考语文作文分数的平均数为22.5×0.05+27.5×0.15+32.5×0.3+37.5×0.2+42.5×0.15+47.5×0.1+52.5×0.05=36.25.
因为(0.01+0.03+0.06)×5=0.5,所以该班这次月考语文作文分数的中位数为35.
20.解:(1)由折线图可知甲射击10次命中的环数分别为9,5,7,8,7,6,8,6,7,7.乙射击10次命中的环数分别为2,4,6,8,7,7,8,9,9,10.
则=×(9+5+7+8+7+6+8+6+7+7)=7(环).
=×(2+4+6+8+7+7+8+9+9+10)=7(环),
=×[(9-7)2+(5-7)2+(7-7)2×4+(6-7)2×2+(8-7)2×2]=1.2,
=×[(2-7)2+(4-7)2+(6-7)2+(7-7)2×2+(8-7)2×2+(9-7)2×2+(10-7)2]=5.4.
(2)因为=,<,
所以甲的射击稳定性比乙好,故甲的射击水平高.
21.解:(1)作出频数分布表,如下.
分组 频数 频率
[0,0.5] 4 0.04
(0.5,1] 8 0.08
(1,1.5] 15 0.15
(1.5,2] 22 0.22
(2,2.5] 25 0.25
(2.5,3] 14 0.14
(3,3.5] 6 0.06
(3.5,4] 4 0.04
(4,4.5] 2 0.02
合计 100 1.00
(2)由频率分布表画出频率分布直方图,如图所示.
由频率分布直方图得这组数据的平均数=0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25×0.06+3.75×0.04+4.25×0.02=2.02.
∵人均月用水量在[0,2]内的频率为0.04+0.08+0.15+0.22=0.49,
在(2,2.5]内的频率为0.25,∴中位数为2+×0.5=2.02.
众数为=2.25.
(3)月用水量在3 t以上的居民的比例为6%+4%+2%=12%,
即大约有12%的居民月用水量在3 t以上,88%的居民月用水量不超过3 t,因此政府的解释是正确的.
22.解:(1)因为0.06×2×1+0.11×2×3+0.18×2×5+0.09×2×7+0.06×2×9=4.92.
因此全市家庭月均用水量平均数的估计值为4.92 t.
(2)频率分布直方图中,用水量低于2 t的频率为0.06×2=0.12.
用水量低于4 t的频率为0.06×2+0.11×2=0.34.
故全市家庭月均用水量的25%分位数的估计值为2+≈3.18(t).
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
