人教版高中数学必修第二册 第十章 概率 单元测试卷(含解析)
文档属性
| 名称 | 人教版高中数学必修第二册 第十章 概率 单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 107.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-19 15:23:33 | ||
图片预览




文档简介
人教版高中数学必修第二册 第十章 概率 单元测试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷60分,第Ⅱ卷90分,共150分,考试时间120分钟.
第Ⅰ卷 (选择题 共60分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.同时抛掷2枚硬币一次,互斥而不对立的两个事件是 ( )
A.“至少有1枚正面朝上”与“2枚都是反面朝上”
B.“至少有1枚正面朝上”与“至少有1枚反面朝上”
C.“恰有1枚正面朝上”与“2枚都是正面朝上”
D.“至少有1枚反面朝上”与“2枚都是反面朝上”
2.一个口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.3,摸出白球的概率是0.2,那么摸出黑球的概率是 ( )
A.0.4 B.0.5 C.0.6 D.0.95
3.甲、乙两位同学进行乒乓球比赛,甲获胜的概率为0.4.现采用随机模拟的方法估计这两位同学打3局比赛时甲恰好获胜2局的概率:先利用计算器产生0到9之间的取整数值的随机数,用1,2,3,4表示甲获胜,用5,6,7,8,9,0表示乙获胜,再以每3个随机数为1组,代表3局比赛的结果.经随机模拟产生了如下30组随机数:
102 231 146 027 590 763 245 207 310 386 350 481 337 286 139
579 684 487 370 175 772 235 246 487 569 047 008 341 287 114
据此估计,这两位同学打3局比赛时甲恰好获胜2局的概率为 ( )
A. B. C. D.
4.已知集合A=,,,,,从A中任意选两个角,其正弦值相等的概率是 ( )
A. B. C. D.
5.某城市2019年的空气质量状况如下表所示:
空气质量指数T 30 60 100 110 130 140
概率P
其中空气质量指数T≤50时,空气质量为优;50A. B. C. D.
6.甲、乙两个实习生每人加工一个零件,他们将零件加工为一等品的概率分别为和,两个零件是否被加工为一等品相互独立,则这两个零件中恰有一个被加工为一等品的概率为 ( )
A. B. C. D.
7.三个元件T1,T2,T3正常工作的概率分别为,,,且它们正常工作与否是相互独立的.如图C5-1,将T2,T3两个元件并联后再与T1元件串联接入电路,则电路不发生故障的概率是 ( )
图C5-1
A. B. C. D.
8.某市对创建全国文明城市工作进行验收时,有关部门对某校高二年级6名学生进行了问卷调查,6人得分分别为5,6,7,8,9,10.把这6名学生的得分看成一个总体.如果用简单随机抽样的方法从这6名学生中抽取2名,他们的得分组成一个样本,则该样本平均数与总体平均数之差的绝对值不超过0.5的概率为 ( )
A. B. C. D.
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,至少有两项是符合题目要求的)
9.从装有大小和形状完全相同的5个红球和3个白球的口袋内任取3个球,那么下列各对事件中,互斥而不对立的是 ( )
A.“至少有1个红球”与“都是红球”
B.“至少有1个红球”与“至少有1个白球”
C.“恰有1个红球”与“恰有2个红球”
D.“至多有1个红球”与“恰有2个红球”
10.下列各对事件中,一定是相互独立事件的有 ( )
A.运动员甲射击一次,“射中9环”与“射中8环”
B.甲、乙两运动员各射击一次,“甲射中10环”与“乙射中9环”
C.甲、乙两运动员各射击一次,“甲、乙都射中目标”与“甲、乙都没有射中目标”
D.甲、乙两运动员各射击一次,“甲射中目标”与“乙未射中目标”
11.一个袋子中装有3件正品和1件次品,按以下要求抽取2件产品,其中结论正确的是 ( )
A.任取2件,则取出的2件中恰有1件次品的概率是
B.每次抽取1件,不放回地抽取两次,样本点的总数为16
C.每次抽取1件,不放回地抽取两次,则取出的2件中恰有1件次品的概率是
D.每次抽取1件,有放回地抽取两次,样本点的总数为16
12.在如图C5-2所示的电路中,A,B,C,D,E这5只箱子表示保险匣,箱中所示数值表示通电时保险丝被烧断的概率,下列结论正确的是 ( )
图C5-2
A.A,B所在线路畅通的概率为
B.A,B,C所在线路畅通的概率为
C.D,E所在线路畅通的概率为
D.当开关闭合时,整个电路畅通的概率为
请将选择题答案填入下表:
题号 1 2 3 4 5 6 7 8 总分
答案
题号 9 10 11 12
答案
第Ⅱ卷 (非选择题 共90分)
三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.若某人在打靶时连续射击2次,则事件“至少有1次中靶”的对立事件是 .
14.一个样本的容量为70,将其分成五组,已知第一组、第三组的频数分别是8,12,第二组、第五组的频率都为,则该样本第四组的频率为 .
15.某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如表所示(单位:名):
参加书法社团 未参加书法社团
参加演讲社团 8 5
未参加演讲社团 2 30
若从该班随机选取1名同学,则该同学至少参加上述一个社团的概率为 .
16.近两年来,以《中国诗词大会》为代表的中国文化类电视节目带动了一股中国文化热潮.某台举办闯关答题比赛,共分两轮,每轮共有4类题型,选手从前往后逐类回答,若中途回答错误,立马淘汰,若全部回答正确,就能获得一枚复活币并进行下一轮答题,两轮都通过就可以获得最终奖金.选手在第一轮闯关获得的复活币,系统会在下一轮答题中自动使用,即下一轮进行闯关答题时,在某一类题型中回答错误,自动复活一次,视为答对该类题型.若某选手每轮的4类题型的通过率均分别为,,,,则该选手获得最终奖金的概率为 .
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)某公司在过去几年内使用某种型号的灯管1000根,该公司对这些灯管的使用寿命(单位:h)进行了统计,统计结果如表所示:
分组 [700,900) [900,1100) [1100,1300) [1300,1500)
频数 48 121 208 223
频率
分组 [1500,1700) [1700,1900) [1900,+∞)
频数 193 165 42
频率
(1)将各组的频率填入表中;
(2)根据上述统计结果,估计该种型号灯管的使用寿命不足1500 h的概率.
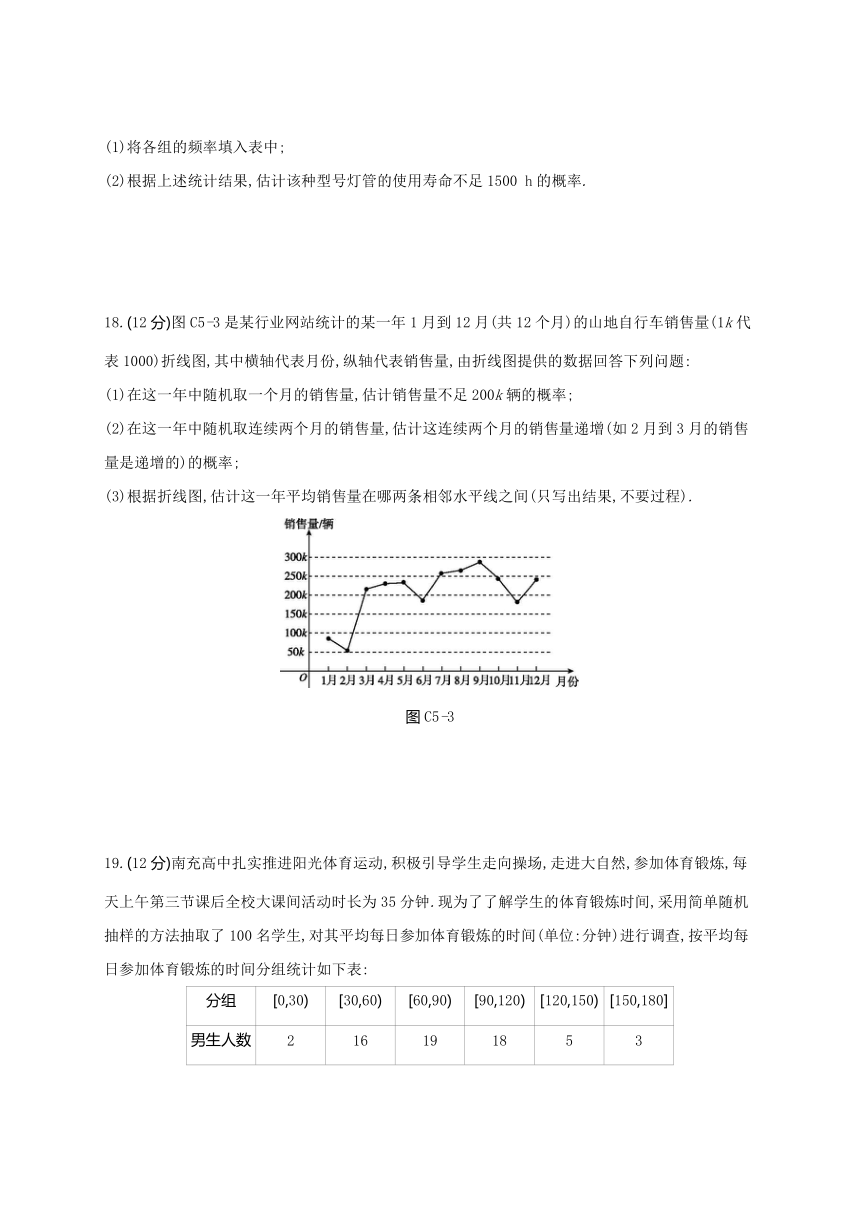
18.(12分)图C5-3是某行业网站统计的某一年1月到12月(共12个月)的山地自行车销售量(1k代表1000)折线图,其中横轴代表月份,纵轴代表销售量,由折线图提供的数据回答下列问题:
(1)在这一年中随机取一个月的销售量,估计销售量不足200k辆的概率;
(2)在这一年中随机取连续两个月的销售量,估计这连续两个月的销售量递增(如2月到3月的销售量是递增的)的概率;
(3)根据折线图,估计这一年平均销售量在哪两条相邻水平线之间(只写出结果,不要过程).
图C5-3
19.(12分)南充高中扎实推进阳光体育运动,积极引导学生走向操场,走进大自然,参加体育锻炼,每天上午第三节课后全校大课间活动时长为35分钟.现为了了解学生的体育锻炼时间,采用简单随机抽样的方法抽取了100名学生,对其平均每日参加体育锻炼的时间(单位:分钟)进行调查,按平均每日参加体育锻炼的时间分组统计如下表:
分组 [0,30) [30,60) [60,90) [90,120) [120,150) [150,180]
男生人数 2 16 19 18 5 3
女生人数 3 20 10 2 1 1
若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.
(1)将频率视为概率,估计该校7000名学生中“锻炼达人”有多少
(2)从这100名学生中的“锻炼达人”中按性别用比例分配的分层随机抽样的方法抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人;
②若从这5人中随机抽取2人作为组长候选人,求抽取的2人中男生和女生各1人的概率.
20.(12分)某套数学试卷中有12道选择题,每道选择题有四个选项,评分标准规定:在每小题给出的四个选项中,只有一项是符合题目要求的,答对得5分,不答或答错得0分.某考生每道选择题都选出一个答案,能确定其中有8道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的,有一道题能判断出一个选项是错误的,还有一道题因不理解题意只能乱猜.试求该考生的选择题:
(1)得60分的概率.
(2)得多少分的概率最大
21.(12分)为防止某突发事件发生,有甲、乙、丙、丁四种相互独立的预防措施可供采用,每钟预防措施最多可以使用一次,单独采用甲、乙、丙、丁预防措施后,此突发事件不发生的概率和所需费用如下表:
预防措施 甲 乙 丙 丁
概率 0.9 0.8 0.7 0.6
费用(万元) 90 60 30 10
预防方案可单独采用一种预防措施或联合采用几种预防措施,在总费用不超过120万元的前提下,请确定一个预防方案,使得此突发事件不发生的概率最大.
22.(12分)甲、乙两人玩卡片游戏:他们手里都拿着分别标有数字1,2,3,4,5,6的6张卡片,各自从自己的卡片中随机抽出1张,规定两人谁抽出的卡片上的数字大,谁就获胜,数字相同则为平局.
(1)求甲获胜的概率.
(2)现已知他们都抽出了标有数字6的卡片,为了分出胜负,他们决定从手里剩下的卡片中再各自随机抽出1张,若他们这次抽出的卡片上数字之和为偶数,则甲获胜,否则乙获胜.请问这个规则公平吗 为什么
参考答案与解析
1.C [解析] 在A中,“至少有1枚正面朝上”与“2枚都是反面朝上”不能同时发生,且“至少有1枚正面朝上”不发生时,“2枚都是反面朝上”一定发生,故A中的两个事件是对立事件;在B中,当2枚硬币恰好1枚正面朝上,1枚反面朝上时,“至少有1枚正面朝上”与“至少有1枚反面朝上”能同时发生,故B中的两个事件不是互斥事件;在C中,“恰有1枚正面朝上”与“2枚都是正面朝上”不能同时发生,且其中一个不发生时,另一个有可能发生也有可能不发生,故C中的两个事件是互斥而不对立事件;在D中,当2枚硬币同时反面朝上时,“至少有1枚反面朝上”“2枚都是反面朝上”能同时发生,故D中的两个事件不是互斥事件.故选C.
2.B [解析] 根据题意可知,从中摸出1个球,“摸出黑球”与“摸出红球”“摸出白球”是互斥事件,故所求概率P=1-0.3-0.2=0.5,故选B.
3.B [解析] 由题意知,在30组随机数中表示两位同学打3局比赛时甲恰好获胜2局的有102,146,245,310,481,337,139,235,246,共9组,故所求概率约为=.故选B.
4.B [解析] 试验“从A中任意选两个角”的样本空间Ω=,,,,,,,,,,,,,,,,,,,,则n(Ω)=10.记事件A=“两个角的正弦值相等”,则A=,,,,,,,,所以n(A)=4,则P(A)===,故选B.
5.A [解析] 由题意,得P(T≤50)=,P(506.B [解析] 记“两个零件中恰好有一个被加工为一等品”为事件A,“甲将零件加工为一等品”为事件A1,“乙将零件加工为一等品”为事件A2,则P(A)=P(A1)+P(A2)=×+×=,故选B.
7.A [解析] 记“T1正常工作”为事件A,“T2正常工作”为事件B,“T3正常工作”为事件C,则P(A)=,P(B)=,P(C)=.电路不发生故障,则须满足T1正常工作,T2,T3中至少有一个正常工作,而T2,T3中至少有一个正常工作的概率P1=1-P( )=1-1-×1-=,则电路不发生故障的概率P=×=,故选A.
8.C [解析] 总体平均数为×(5+6+7+8+9+10)=7.5.“抽取2名学生”的样本空间Ω={(5,6),(5,7),(5,8),(5,9),(5,10),(6,7),(6,8),(6,9),(6,10),(7,8),(7,9),(7,10),(8,9),(8,10),(9,10)},则n(Ω)=15.记事件A=“样本平均数与总体平均数之差的绝对值不超过0.5”,则A={(5,9),(5,10),(6,8),(6,9),(6,10),(7,8),(7,9)},所以n(A)=7,则P(A)==,故选C.
9.CD [解析] 根据互斥事件与对立事件的定义判断.A中两事件不是互斥事件,事件“都是红球”是两事件的交事件;B中两事件能同时发生,如“恰有1个红球和2个白球”发生时,两事件均发生,故不是互斥事件;C中两事件是互斥而不对立事件;“至多有1个红球”,即“有0个或1个红球”,与“恰有2个红球”互斥,除此之外事件“都是红球”也可能发生,因此它们不对立,D符合题意.故选CD.
10.BD [解析] 在A中,甲射击一次,“射中9环”与“射中8环”是互斥事件,不会同时发生,因此不是相互独立事件;在B中,甲、乙各射击一次,“甲射中10环”发生与否对“乙射中9环”的概率没有影响,二者是相互独立事件;在C中,甲、乙各射击一次,“甲、乙都射中目标”与“甲、乙都没有射中目标”相互独立事件;在D中,甲、乙各射击一次,“甲射中目标”发生与否对“乙未射中目标”的概率没有影响,二者一定是相互独立事件.故选BD.
11.ACD [解析] 记4件产品分别为1,2,3,a,其中a表示次品.对于A,样本空间Ω={(1,2),(1,3),(1,a),(2,3),(2,a),(3,a)},“恰有一件次品”包含的样本点为(1,a),(2,a),(3,a),因此其概率P==,A正确;对于B,每次抽取1件,不放回地抽取两次,样本空间Ω={(1,2),(1,3),(1,a),(2,1),(2,3),(2,a),(3,1),(3,2),(3,a),(a,1)(a,2),(a,3)},因此n(Ω)=12,B错误;对于C,“取出的2件中恰有1件次品”包含的样本点的个数为6,故其概率为,C正确;对于D,每次抽取1件,有放回地抽取两次,样本空间Ω={(1,1),(1,2),(1,3),(1,a),(2,1),(2,2),(2,3),(2,a),(3,1),(3,2),(3,3),(3,a),(a,1),(a,2),(a,3),(a,a)},因此n(Ω)=16,D正确.故选ACD.
12.BD [解析] 由题意知,A,B,C,D,E表示的保险闸中的保险丝被烧断的概率分别为,,,,,所以A,B所在线路畅通的概率为×=,故A错误;D,E并联后的电路畅通的概率为1-×=1-=,故C错误;A,B,C所在线路畅通的概率为1-×=1-=,故B正确;根据上述分析可知,当开关闭合时,整个电路畅通的概率为×=,故D正确.故选BD.
13.“2次都未中靶” [解析] 由对立事件的概念可得.
14. [解析] 根据题意可得第一组和第三组的频率分别为=,=.根据各组的频率之和为1,即可求得第四组的频率为1---=.
15. [解析] 由题意得该班一共有45名学生,其中两个社团都未参加的有30人,∴从该班随机选取1名同学,则该同学至少参加上述一个社团的概率P=1-=.
16. [解析] 选手进入第二轮答题,则第一轮中答题全部正确,其概率为×××=.结束第一轮答题后,选手通过第二轮答题的概率为+×××+×××+×××+×××=++++=,故该选手获得最终奖金的概率为×=.
17.解:(1)
分组 [700,900) [900,1100) [1100,1300) [1300,1500)
频数 48 121 208 223
频率 0.048 0.121 0.208 0.223
分组 [1500,1700) [1700,1900) [1900,+∞)
频数 193 165 42
频率 0.193 0.165 0.042
(2)这1000根灯管中使用寿命不足1500 h的频数是48+121+208+223=600,所以其频率是=0.6,由此可估计该种型号灯管的使用寿命不足1500 h的概率约为0.6.
18.解:(1)“随机取一个月的销售量”的样本空间的样本点有12个,记事件A=“销售量不足200k辆”,
则A={1月,2月,6月,11月},所以P(A)==.
(2)“取连续两个月的销售量”的样本空间Ω={1,2月;2,3月;3,4月;4,5月;5,6月;6,7月;7,8月;8,9月;9,10月;10,11月;11,12月},则n(Ω)=11.
记事件B=“连续两个月的销售量递增”,
则B={2,3月,3,4月;4,5月;6,7月;7,8月;8,9月;11,12月},所以n(B)=7,
则P(B)==.
(3)由折线图知,年平均销售量在150k~200k这两条水平线之间.
19.解:(1)由表可知,100名学生中“锻炼达人”的人数为10,将频率视为概率,我校7000名学生中“锻炼达人”约有7000×=700(名).
(2)①由(1)知100名学生中的“锻炼达人”有10人,其中男生8人,女生2人.
从10人中按性别用比例分配的分层随机抽样的方法抽取5人参加体育活动,则男生抽取4人,女生抽取1人.
②“从5人中抽取2人”的样本空间Ω={男1男2,男1男3,男1 男4,男1女,男2男3,男2男4,男2女,男3男4,男3女,男4女},则n(Ω)=10.
记事件A=“抽取的2人中男生和女生各1人”,则A={男1女,男2女,男3女,男4女},则n(A)=4,所以P(A)===.
20.解:(1)要得60分,必须12道选择题全答对,
依题意,易知在其余4道题中,有两道题答对的概率各为,有一道题答对的概率为,还有一道题答对的概率为,
所以该考生的选择题得60分的概率P=×××=.
(2)依题意,该考生选择题得分的可能取值有40,45,50,55,60,共5种.
得40分的概率P1=×××==;
得45分的概率P2=2××××+×××+×××=;
得50分的概率P3=×××+2××××+2××××+×××=;
得55分的概率P4=×××+×××+2××××=;
得60分的概率P5=×××=.
所以该考生选择题得45分或50分的概率最大.
21.解:方案1:单独采用甲、乙、丙、丁四种预防措施中的一种,所需费用均不超过120万元.由表可知,采用甲措施可使此突发事件不发生的概率最大,其概率为0.9.
方案2:联合采用两种预防措施,总费用不超过120万元.由表可知,联合采用甲、丙两种预防措施,可使此突发事件不发生的概率为1-(1-0.9)×(1-0.7)=0.97.
联合采用甲、丁或乙、丙或乙、丁或丙、丁两种预防措施,此突发事件不发生的概率分别为0.96,0.94,0.92,0.88,其概率均小于0.97,所以联合采用甲、丙两种预防措施,可使此突发事件不发生的概率最大,其概率为0.97.
方案3:联合采用三种预防措施,由于总费用不能超过120万元,故只能联合采用乙、丙、丁三种预防措施.
此时突发事件不发生的概率为1-(1-0.8)×(1-0.7)×(1-0.6)=0.976.
综上所述,在总费用不超过120万元的前提下,联合采用乙、丙、丁三种预防措施,可使突发事件不发生的概率最大.
22.解:分别用x,y表示甲、乙抽出的卡片上的数字,则样本点可用(x,y)表示“两人各自从自己的卡片中随机抽出1张”的样本空间Ω1={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)},则n(Ω1)=36.
记事件A=“甲获胜”,则A={(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),(6,4),(6,5)},则n(A)=15,
所以P(A)===.
(2)“各自从手里剩下的卡片中随机抽出1张”的样本空间Ω2={(1,1),(1,2),(1,3),(1,4),(1,5),(2,1),(2,2),(2,3),(2,4),(2,5),(3,1),(3,2),(3,3),(3,4),(3,5),(4,1),(4,2),(4,3),(4,4), (4,5),(5,1),(5,2),(5,3),(5,4),(5,5)},则n(Ω2)=25.
记事件B=“卡片上的数字之和为偶数”,则B={(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),(4,2),(4,4),(5,1),(5,3),(5,5)},则n(B)=13,
所以P(B)==,
所以根据规则,甲获胜的概率为,乙获胜的概率为,所以这个规则不公平.
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷60分,第Ⅱ卷90分,共150分,考试时间120分钟.
第Ⅰ卷 (选择题 共60分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.同时抛掷2枚硬币一次,互斥而不对立的两个事件是 ( )
A.“至少有1枚正面朝上”与“2枚都是反面朝上”
B.“至少有1枚正面朝上”与“至少有1枚反面朝上”
C.“恰有1枚正面朝上”与“2枚都是正面朝上”
D.“至少有1枚反面朝上”与“2枚都是反面朝上”
2.一个口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.3,摸出白球的概率是0.2,那么摸出黑球的概率是 ( )
A.0.4 B.0.5 C.0.6 D.0.95
3.甲、乙两位同学进行乒乓球比赛,甲获胜的概率为0.4.现采用随机模拟的方法估计这两位同学打3局比赛时甲恰好获胜2局的概率:先利用计算器产生0到9之间的取整数值的随机数,用1,2,3,4表示甲获胜,用5,6,7,8,9,0表示乙获胜,再以每3个随机数为1组,代表3局比赛的结果.经随机模拟产生了如下30组随机数:
102 231 146 027 590 763 245 207 310 386 350 481 337 286 139
579 684 487 370 175 772 235 246 487 569 047 008 341 287 114
据此估计,这两位同学打3局比赛时甲恰好获胜2局的概率为 ( )
A. B. C. D.
4.已知集合A=,,,,,从A中任意选两个角,其正弦值相等的概率是 ( )
A. B. C. D.
5.某城市2019年的空气质量状况如下表所示:
空气质量指数T 30 60 100 110 130 140
概率P
其中空气质量指数T≤50时,空气质量为优;50
6.甲、乙两个实习生每人加工一个零件,他们将零件加工为一等品的概率分别为和,两个零件是否被加工为一等品相互独立,则这两个零件中恰有一个被加工为一等品的概率为 ( )
A. B. C. D.
7.三个元件T1,T2,T3正常工作的概率分别为,,,且它们正常工作与否是相互独立的.如图C5-1,将T2,T3两个元件并联后再与T1元件串联接入电路,则电路不发生故障的概率是 ( )
图C5-1
A. B. C. D.
8.某市对创建全国文明城市工作进行验收时,有关部门对某校高二年级6名学生进行了问卷调查,6人得分分别为5,6,7,8,9,10.把这6名学生的得分看成一个总体.如果用简单随机抽样的方法从这6名学生中抽取2名,他们的得分组成一个样本,则该样本平均数与总体平均数之差的绝对值不超过0.5的概率为 ( )
A. B. C. D.
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,至少有两项是符合题目要求的)
9.从装有大小和形状完全相同的5个红球和3个白球的口袋内任取3个球,那么下列各对事件中,互斥而不对立的是 ( )
A.“至少有1个红球”与“都是红球”
B.“至少有1个红球”与“至少有1个白球”
C.“恰有1个红球”与“恰有2个红球”
D.“至多有1个红球”与“恰有2个红球”
10.下列各对事件中,一定是相互独立事件的有 ( )
A.运动员甲射击一次,“射中9环”与“射中8环”
B.甲、乙两运动员各射击一次,“甲射中10环”与“乙射中9环”
C.甲、乙两运动员各射击一次,“甲、乙都射中目标”与“甲、乙都没有射中目标”
D.甲、乙两运动员各射击一次,“甲射中目标”与“乙未射中目标”
11.一个袋子中装有3件正品和1件次品,按以下要求抽取2件产品,其中结论正确的是 ( )
A.任取2件,则取出的2件中恰有1件次品的概率是
B.每次抽取1件,不放回地抽取两次,样本点的总数为16
C.每次抽取1件,不放回地抽取两次,则取出的2件中恰有1件次品的概率是
D.每次抽取1件,有放回地抽取两次,样本点的总数为16
12.在如图C5-2所示的电路中,A,B,C,D,E这5只箱子表示保险匣,箱中所示数值表示通电时保险丝被烧断的概率,下列结论正确的是 ( )
图C5-2
A.A,B所在线路畅通的概率为
B.A,B,C所在线路畅通的概率为
C.D,E所在线路畅通的概率为
D.当开关闭合时,整个电路畅通的概率为
请将选择题答案填入下表:
题号 1 2 3 4 5 6 7 8 总分
答案
题号 9 10 11 12
答案
第Ⅱ卷 (非选择题 共90分)
三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.若某人在打靶时连续射击2次,则事件“至少有1次中靶”的对立事件是 .
14.一个样本的容量为70,将其分成五组,已知第一组、第三组的频数分别是8,12,第二组、第五组的频率都为,则该样本第四组的频率为 .
15.某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如表所示(单位:名):
参加书法社团 未参加书法社团
参加演讲社团 8 5
未参加演讲社团 2 30
若从该班随机选取1名同学,则该同学至少参加上述一个社团的概率为 .
16.近两年来,以《中国诗词大会》为代表的中国文化类电视节目带动了一股中国文化热潮.某台举办闯关答题比赛,共分两轮,每轮共有4类题型,选手从前往后逐类回答,若中途回答错误,立马淘汰,若全部回答正确,就能获得一枚复活币并进行下一轮答题,两轮都通过就可以获得最终奖金.选手在第一轮闯关获得的复活币,系统会在下一轮答题中自动使用,即下一轮进行闯关答题时,在某一类题型中回答错误,自动复活一次,视为答对该类题型.若某选手每轮的4类题型的通过率均分别为,,,,则该选手获得最终奖金的概率为 .
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)某公司在过去几年内使用某种型号的灯管1000根,该公司对这些灯管的使用寿命(单位:h)进行了统计,统计结果如表所示:
分组 [700,900) [900,1100) [1100,1300) [1300,1500)
频数 48 121 208 223
频率
分组 [1500,1700) [1700,1900) [1900,+∞)
频数 193 165 42
频率
(1)将各组的频率填入表中;
(2)根据上述统计结果,估计该种型号灯管的使用寿命不足1500 h的概率.
18.(12分)图C5-3是某行业网站统计的某一年1月到12月(共12个月)的山地自行车销售量(1k代表1000)折线图,其中横轴代表月份,纵轴代表销售量,由折线图提供的数据回答下列问题:
(1)在这一年中随机取一个月的销售量,估计销售量不足200k辆的概率;
(2)在这一年中随机取连续两个月的销售量,估计这连续两个月的销售量递增(如2月到3月的销售量是递增的)的概率;
(3)根据折线图,估计这一年平均销售量在哪两条相邻水平线之间(只写出结果,不要过程).
图C5-3
19.(12分)南充高中扎实推进阳光体育运动,积极引导学生走向操场,走进大自然,参加体育锻炼,每天上午第三节课后全校大课间活动时长为35分钟.现为了了解学生的体育锻炼时间,采用简单随机抽样的方法抽取了100名学生,对其平均每日参加体育锻炼的时间(单位:分钟)进行调查,按平均每日参加体育锻炼的时间分组统计如下表:
分组 [0,30) [30,60) [60,90) [90,120) [120,150) [150,180]
男生人数 2 16 19 18 5 3
女生人数 3 20 10 2 1 1
若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.
(1)将频率视为概率,估计该校7000名学生中“锻炼达人”有多少
(2)从这100名学生中的“锻炼达人”中按性别用比例分配的分层随机抽样的方法抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人;
②若从这5人中随机抽取2人作为组长候选人,求抽取的2人中男生和女生各1人的概率.
20.(12分)某套数学试卷中有12道选择题,每道选择题有四个选项,评分标准规定:在每小题给出的四个选项中,只有一项是符合题目要求的,答对得5分,不答或答错得0分.某考生每道选择题都选出一个答案,能确定其中有8道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的,有一道题能判断出一个选项是错误的,还有一道题因不理解题意只能乱猜.试求该考生的选择题:
(1)得60分的概率.
(2)得多少分的概率最大
21.(12分)为防止某突发事件发生,有甲、乙、丙、丁四种相互独立的预防措施可供采用,每钟预防措施最多可以使用一次,单独采用甲、乙、丙、丁预防措施后,此突发事件不发生的概率和所需费用如下表:
预防措施 甲 乙 丙 丁
概率 0.9 0.8 0.7 0.6
费用(万元) 90 60 30 10
预防方案可单独采用一种预防措施或联合采用几种预防措施,在总费用不超过120万元的前提下,请确定一个预防方案,使得此突发事件不发生的概率最大.
22.(12分)甲、乙两人玩卡片游戏:他们手里都拿着分别标有数字1,2,3,4,5,6的6张卡片,各自从自己的卡片中随机抽出1张,规定两人谁抽出的卡片上的数字大,谁就获胜,数字相同则为平局.
(1)求甲获胜的概率.
(2)现已知他们都抽出了标有数字6的卡片,为了分出胜负,他们决定从手里剩下的卡片中再各自随机抽出1张,若他们这次抽出的卡片上数字之和为偶数,则甲获胜,否则乙获胜.请问这个规则公平吗 为什么
参考答案与解析
1.C [解析] 在A中,“至少有1枚正面朝上”与“2枚都是反面朝上”不能同时发生,且“至少有1枚正面朝上”不发生时,“2枚都是反面朝上”一定发生,故A中的两个事件是对立事件;在B中,当2枚硬币恰好1枚正面朝上,1枚反面朝上时,“至少有1枚正面朝上”与“至少有1枚反面朝上”能同时发生,故B中的两个事件不是互斥事件;在C中,“恰有1枚正面朝上”与“2枚都是正面朝上”不能同时发生,且其中一个不发生时,另一个有可能发生也有可能不发生,故C中的两个事件是互斥而不对立事件;在D中,当2枚硬币同时反面朝上时,“至少有1枚反面朝上”“2枚都是反面朝上”能同时发生,故D中的两个事件不是互斥事件.故选C.
2.B [解析] 根据题意可知,从中摸出1个球,“摸出黑球”与“摸出红球”“摸出白球”是互斥事件,故所求概率P=1-0.3-0.2=0.5,故选B.
3.B [解析] 由题意知,在30组随机数中表示两位同学打3局比赛时甲恰好获胜2局的有102,146,245,310,481,337,139,235,246,共9组,故所求概率约为=.故选B.
4.B [解析] 试验“从A中任意选两个角”的样本空间Ω=,,,,,,,,,,,,,,,,,,,,则n(Ω)=10.记事件A=“两个角的正弦值相等”,则A=,,,,,,,,所以n(A)=4,则P(A)===,故选B.
5.A [解析] 由题意,得P(T≤50)=,P(50
7.A [解析] 记“T1正常工作”为事件A,“T2正常工作”为事件B,“T3正常工作”为事件C,则P(A)=,P(B)=,P(C)=.电路不发生故障,则须满足T1正常工作,T2,T3中至少有一个正常工作,而T2,T3中至少有一个正常工作的概率P1=1-P( )=1-1-×1-=,则电路不发生故障的概率P=×=,故选A.
8.C [解析] 总体平均数为×(5+6+7+8+9+10)=7.5.“抽取2名学生”的样本空间Ω={(5,6),(5,7),(5,8),(5,9),(5,10),(6,7),(6,8),(6,9),(6,10),(7,8),(7,9),(7,10),(8,9),(8,10),(9,10)},则n(Ω)=15.记事件A=“样本平均数与总体平均数之差的绝对值不超过0.5”,则A={(5,9),(5,10),(6,8),(6,9),(6,10),(7,8),(7,9)},所以n(A)=7,则P(A)==,故选C.
9.CD [解析] 根据互斥事件与对立事件的定义判断.A中两事件不是互斥事件,事件“都是红球”是两事件的交事件;B中两事件能同时发生,如“恰有1个红球和2个白球”发生时,两事件均发生,故不是互斥事件;C中两事件是互斥而不对立事件;“至多有1个红球”,即“有0个或1个红球”,与“恰有2个红球”互斥,除此之外事件“都是红球”也可能发生,因此它们不对立,D符合题意.故选CD.
10.BD [解析] 在A中,甲射击一次,“射中9环”与“射中8环”是互斥事件,不会同时发生,因此不是相互独立事件;在B中,甲、乙各射击一次,“甲射中10环”发生与否对“乙射中9环”的概率没有影响,二者是相互独立事件;在C中,甲、乙各射击一次,“甲、乙都射中目标”与“甲、乙都没有射中目标”相互独立事件;在D中,甲、乙各射击一次,“甲射中目标”发生与否对“乙未射中目标”的概率没有影响,二者一定是相互独立事件.故选BD.
11.ACD [解析] 记4件产品分别为1,2,3,a,其中a表示次品.对于A,样本空间Ω={(1,2),(1,3),(1,a),(2,3),(2,a),(3,a)},“恰有一件次品”包含的样本点为(1,a),(2,a),(3,a),因此其概率P==,A正确;对于B,每次抽取1件,不放回地抽取两次,样本空间Ω={(1,2),(1,3),(1,a),(2,1),(2,3),(2,a),(3,1),(3,2),(3,a),(a,1)(a,2),(a,3)},因此n(Ω)=12,B错误;对于C,“取出的2件中恰有1件次品”包含的样本点的个数为6,故其概率为,C正确;对于D,每次抽取1件,有放回地抽取两次,样本空间Ω={(1,1),(1,2),(1,3),(1,a),(2,1),(2,2),(2,3),(2,a),(3,1),(3,2),(3,3),(3,a),(a,1),(a,2),(a,3),(a,a)},因此n(Ω)=16,D正确.故选ACD.
12.BD [解析] 由题意知,A,B,C,D,E表示的保险闸中的保险丝被烧断的概率分别为,,,,,所以A,B所在线路畅通的概率为×=,故A错误;D,E并联后的电路畅通的概率为1-×=1-=,故C错误;A,B,C所在线路畅通的概率为1-×=1-=,故B正确;根据上述分析可知,当开关闭合时,整个电路畅通的概率为×=,故D正确.故选BD.
13.“2次都未中靶” [解析] 由对立事件的概念可得.
14. [解析] 根据题意可得第一组和第三组的频率分别为=,=.根据各组的频率之和为1,即可求得第四组的频率为1---=.
15. [解析] 由题意得该班一共有45名学生,其中两个社团都未参加的有30人,∴从该班随机选取1名同学,则该同学至少参加上述一个社团的概率P=1-=.
16. [解析] 选手进入第二轮答题,则第一轮中答题全部正确,其概率为×××=.结束第一轮答题后,选手通过第二轮答题的概率为+×××+×××+×××+×××=++++=,故该选手获得最终奖金的概率为×=.
17.解:(1)
分组 [700,900) [900,1100) [1100,1300) [1300,1500)
频数 48 121 208 223
频率 0.048 0.121 0.208 0.223
分组 [1500,1700) [1700,1900) [1900,+∞)
频数 193 165 42
频率 0.193 0.165 0.042
(2)这1000根灯管中使用寿命不足1500 h的频数是48+121+208+223=600,所以其频率是=0.6,由此可估计该种型号灯管的使用寿命不足1500 h的概率约为0.6.
18.解:(1)“随机取一个月的销售量”的样本空间的样本点有12个,记事件A=“销售量不足200k辆”,
则A={1月,2月,6月,11月},所以P(A)==.
(2)“取连续两个月的销售量”的样本空间Ω={1,2月;2,3月;3,4月;4,5月;5,6月;6,7月;7,8月;8,9月;9,10月;10,11月;11,12月},则n(Ω)=11.
记事件B=“连续两个月的销售量递增”,
则B={2,3月,3,4月;4,5月;6,7月;7,8月;8,9月;11,12月},所以n(B)=7,
则P(B)==.
(3)由折线图知,年平均销售量在150k~200k这两条水平线之间.
19.解:(1)由表可知,100名学生中“锻炼达人”的人数为10,将频率视为概率,我校7000名学生中“锻炼达人”约有7000×=700(名).
(2)①由(1)知100名学生中的“锻炼达人”有10人,其中男生8人,女生2人.
从10人中按性别用比例分配的分层随机抽样的方法抽取5人参加体育活动,则男生抽取4人,女生抽取1人.
②“从5人中抽取2人”的样本空间Ω={男1男2,男1男3,男1 男4,男1女,男2男3,男2男4,男2女,男3男4,男3女,男4女},则n(Ω)=10.
记事件A=“抽取的2人中男生和女生各1人”,则A={男1女,男2女,男3女,男4女},则n(A)=4,所以P(A)===.
20.解:(1)要得60分,必须12道选择题全答对,
依题意,易知在其余4道题中,有两道题答对的概率各为,有一道题答对的概率为,还有一道题答对的概率为,
所以该考生的选择题得60分的概率P=×××=.
(2)依题意,该考生选择题得分的可能取值有40,45,50,55,60,共5种.
得40分的概率P1=×××==;
得45分的概率P2=2××××+×××+×××=;
得50分的概率P3=×××+2××××+2××××+×××=;
得55分的概率P4=×××+×××+2××××=;
得60分的概率P5=×××=.
所以该考生选择题得45分或50分的概率最大.
21.解:方案1:单独采用甲、乙、丙、丁四种预防措施中的一种,所需费用均不超过120万元.由表可知,采用甲措施可使此突发事件不发生的概率最大,其概率为0.9.
方案2:联合采用两种预防措施,总费用不超过120万元.由表可知,联合采用甲、丙两种预防措施,可使此突发事件不发生的概率为1-(1-0.9)×(1-0.7)=0.97.
联合采用甲、丁或乙、丙或乙、丁或丙、丁两种预防措施,此突发事件不发生的概率分别为0.96,0.94,0.92,0.88,其概率均小于0.97,所以联合采用甲、丙两种预防措施,可使此突发事件不发生的概率最大,其概率为0.97.
方案3:联合采用三种预防措施,由于总费用不能超过120万元,故只能联合采用乙、丙、丁三种预防措施.
此时突发事件不发生的概率为1-(1-0.8)×(1-0.7)×(1-0.6)=0.976.
综上所述,在总费用不超过120万元的前提下,联合采用乙、丙、丁三种预防措施,可使突发事件不发生的概率最大.
22.解:分别用x,y表示甲、乙抽出的卡片上的数字,则样本点可用(x,y)表示“两人各自从自己的卡片中随机抽出1张”的样本空间Ω1={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)},则n(Ω1)=36.
记事件A=“甲获胜”,则A={(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),(6,4),(6,5)},则n(A)=15,
所以P(A)===.
(2)“各自从手里剩下的卡片中随机抽出1张”的样本空间Ω2={(1,1),(1,2),(1,3),(1,4),(1,5),(2,1),(2,2),(2,3),(2,4),(2,5),(3,1),(3,2),(3,3),(3,4),(3,5),(4,1),(4,2),(4,3),(4,4), (4,5),(5,1),(5,2),(5,3),(5,4),(5,5)},则n(Ω2)=25.
记事件B=“卡片上的数字之和为偶数”,则B={(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),(4,2),(4,4),(5,1),(5,3),(5,5)},则n(B)=13,
所以P(B)==,
所以根据规则,甲获胜的概率为,乙获胜的概率为,所以这个规则不公平.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
