人教版高中数学必修第二册8.5.1-8.5.2 直线与直线、直线与平面平行 同步精练(含解析)
文档属性
| 名称 | 人教版高中数学必修第二册8.5.1-8.5.2 直线与直线、直线与平面平行 同步精练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-19 15:28:05 | ||
图片预览



文档简介
人教版高中数学必修第二册8.5.1-8.5.2 直线与直线、直线与平面平行 同步精练
【考点梳理】
考点一 基本事实4
文字语言 平行于同一条直线的两条直线平行
图形语言
符号语言 直线a,b,c,a∥b,b∥c a∥c
作用 证明两条直线平行
说明 基本事实4表述的性质通常叫做平行线的传递性
考点二 空间等角定理
1.定理
文字语言 如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补
符号语言 OA∥O′A′,OB∥O′B′ ∠AOB=∠A′O′B′或∠AOB+∠A′O′B′=180°
图形语言
作用 判断或证明两个角相等或互补
2.推广
如果两条相交直线与另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.
考点三 直线与平面平行的判定定理
文字语言 如果平面外一条直线与此平面内一条直线平行,那么该直线与此平面平行
符号语言 a∥α
图形语言
考点四 直线与平面平行的性质定理
文字语言 一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行
符号语言 a∥α,a β,α∩β=b a∥b
图形语言
【题型归纳】
题型一:等角定理
1.若,且,与方向相同,则下列结论正确的有( )
A.且方向相同 B.,方向可能不同
C.OB与不平行 D.OB与不一定平行
2.在正方体中,,,分别为棱,,的中点,试证明:.
3.如图,三棱柱中,,,分别为,,的中点.求证:.
题型二:直线与平面平行的判定定理的应用
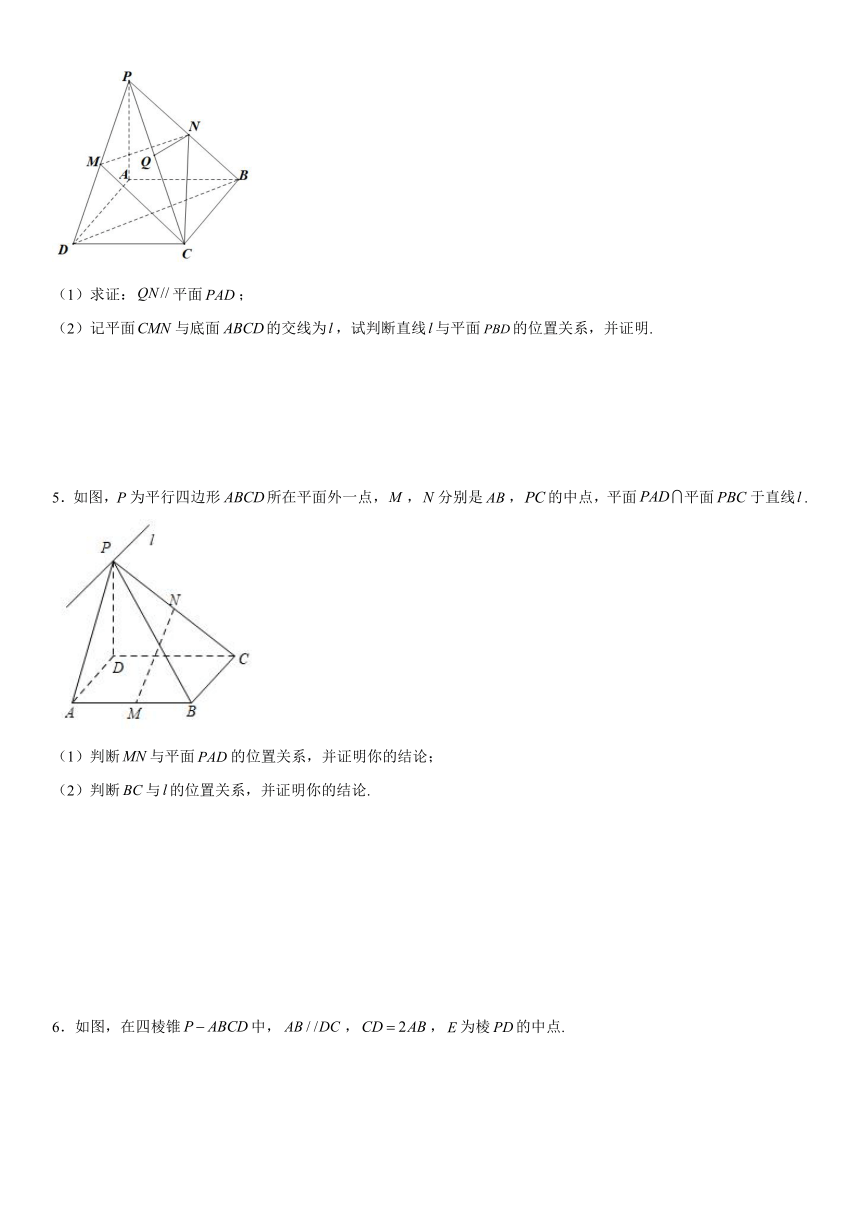
4.如图,在四棱锥中,底面是菱形,分别为,,的中点.
(1)求证:平面;
(2)记平面与底面的交线为,试判断直线与平面的位置关系,并证明.
5.如图,P为平行四边形所在平面外一点,,分别是,的中点,平面平面于直线.
(1)判断与平面的位置关系,并证明你的结论;
(2)判断与的位置关系,并证明你的结论.
6.如图,在四棱锥中,,,为棱的中点.
(1)求证:平面;
(2)试判断与平面是否平行?并说明理由.
题型三:直线与平面平行的性质判断线段比例或点所在位置
7.如图,已知四棱锥的底面是菱形,交于点O,E为的中点,F在上,,∥平面,则的值为( )
A.1 B. C.3 D.2
8.如图,在三棱锥P—ABC中,点D,E分别为棱PB,BC的中点.若点F在线段AC上,且满足AD平面PEF,则的值为( )
A.1 B.2 C. D.
9.如图,已知四棱维的底面是平行四边形,交于点,为中点,在上,,平面,则的值为( )
A. B. C. D.
题型四:直线与平面平行的性质定理的应用
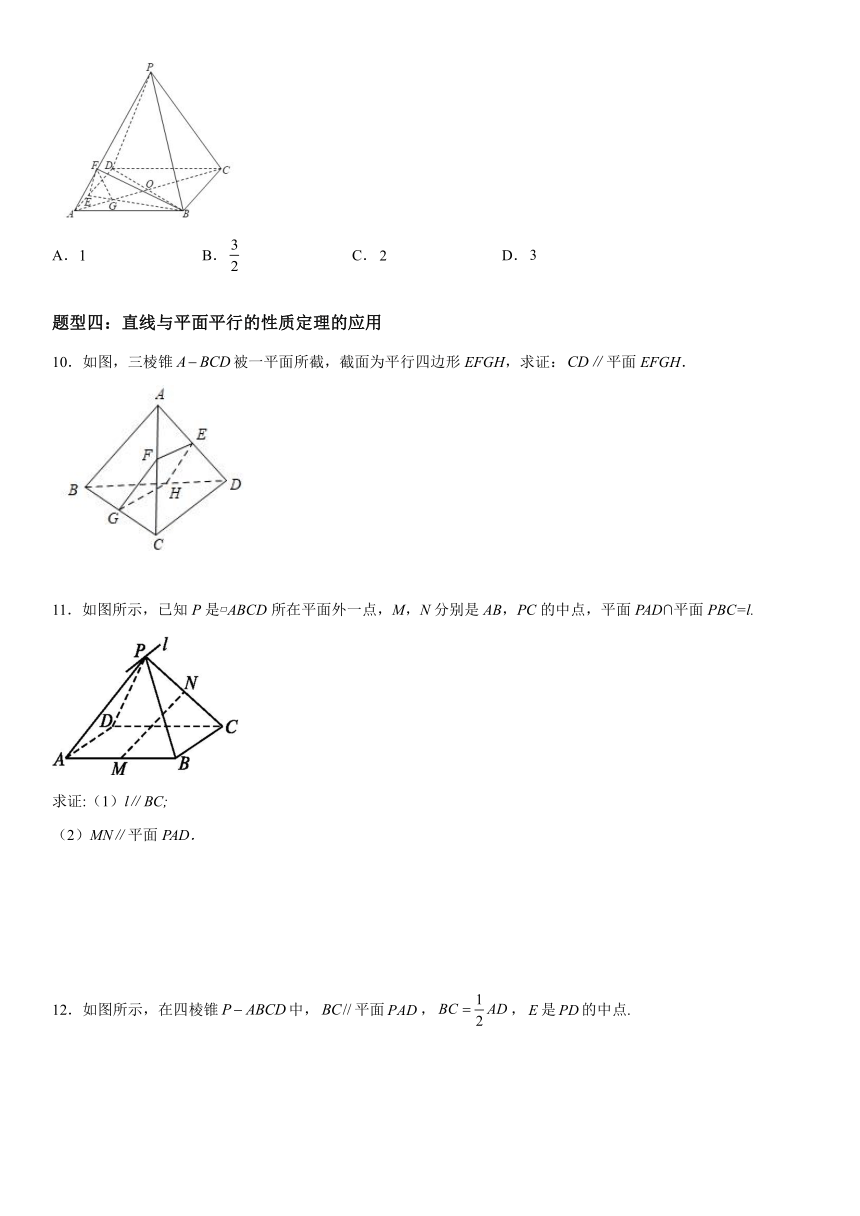
10.如图,三棱锥被一平面所截,截面为平行四边形EFGH,求证:平面EFGH.
11.如图所示,已知P是 ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.
求证:(1)l∥BC;
(2)MN∥平面PAD.
12.如图所示,在四棱锥中,平面,,是的中点.
(1)求证:;
(2)求证:平面;
(3)若是线段上一动点,则线段上是否存在点,使平面?说明理由.
【双基达标】
一、单选题
13.对于直线m,n和平面α,下列命题中正确的是( )
A.如果m α,nα,m,n是异面直线,那么nα
B.如果m α,nα,m,n是异面直线,那么n与α相交
C.如果m α,nα,m,n共面,那么mn
D.如果mα,nα,m,n共面,那么mn
14.已知直线和平面,下列说法正确的是( )
A.如果,那么平行于经过的任意一个平面.
B.如果,那么平行于平面内的任意一条直线.
C.若,则 .
D.若且,则.
15.已知m,n为两条不同的直线,,为两个不同的平面,则下列结论中正确的是( )
A.若,,则
B.若,n,则
C.若,m,=n,则
D.若,,则
16.如图,在四面体ABCD中,若截面PQMN是正方形,则在下列说法中,错误的为( )
A.AC⊥BD B.AC=BD C.AC∥截面PQMN D.异面直线PM与BD所成的角为45°
17.如图,在四棱锥中,底面ABCD为菱形,,Q为AD的中点,点M在线段PC上,,若平面MQB,则t等于( )
A. B. C. D.
18.如图所示,P为矩形所在平面外一点,矩形对角线交点为为的中点,给出五个结论:①;②平面;③平面;④平面;⑤平面.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
19.下列结论中正确的是( )
①在空间中,若两条直线不相交,则它们一定平行;②平行于同一条直线的两条直线平行;③一条直线和两条平行直线中的一条相交,那么它也和另一条相交;④空间中有四条直线a,b,c,d,如果ab,cd,且ad,那么bc.
A.①②③ B.②④ C.③④ D.②③
20.下列命题的符号语言中,不是公理的是( )
A.,
B.,且,且
C.,,且,
D.,
21.如图所示,在空间四边形ABCD中,E,F分别为边AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则( )
A.BD平面EFGH,且四边形EFGH是矩形
B.EF平面BCD,且四边形EFGH是梯形
C.HG平面ABD,且四边形EFGH是菱形
D.EH平面ADC,且四边形EFGH是平行四边形
【高分突破】
一:单选题
22.如图,在直四棱柱中,下列结论正确的是( )
A.与是两条相交直线
B.平面
C.
D.,,,四点共面
23.在空间四边形中,分别在上,且满足,则直线与平面的位置关系是( )
A.平面 B.平面
C.与平面相交 D.以上都有可能
24.如图所示,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,下列结论正确的个数为( )
①平面PBC ②平面PCD ③平面PDA ④平面PBA
A.1个 B.2个 C.3个 D.4个
二、多选题
25.(多选题)下列命题中,错误的结论有( )
A.如果一个角的两边与另一个角的两边分别平行,那么这两个角相等
B.如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等
C.如果一个角的两边和另一个角的两边分别垂直,那么这两个角相等或互补
D.如果两条直线同时平行于第三条直线,那么这两条直线互相平行
26.如图,在四面体中,截面是正方形,则( )
A. B.平面
C. D.分别是线段的中点
27.如图所示,在棱长为2的正方体中,,,分别为所在棱的中点,为正方形内(包括边界)一动点,且平面,则( )
A. B.平面
C.三棱锥的体积为1 D.只能在线段上
28.在正方体中,、、分别为,,的中点则( )
A.直线与直线垂直
B.直线与平面平行
C.平面截正方体所得的截而是等腰梯形
D.点和点到平面的距离相等
29.已知图1中的正三棱柱的底面边长为2,体积为,去掉其侧棱,再将上底面绕上下底面的中心所在的直线,逆时针旋转后,添上侧棱,得到图2所示的几何体,则下列说法正确的是( )
图1 图2
A.平面ABC
B.
C.四边形为正方形
D.正三棱柱,与几何体的外接球体积相同
三、填空题
30.已知l,m,n是互不相同的直线,α,β,γ是三个不同的平面,给出下列命题:
①若l与m为异面直线,l α,m β,则αβ;
②若αβ,l α,m β,则lm;
③若α∩β=l,β∩γ=m,γ∩α=n,lγ,则mn.
其中所有真命题的序号为________.
31.如图所示,直线平面,点平面,并且直线a和点A位于平面两侧,点B,C,,AB,AC,AD分别交平面于点E,F,G,若,,,则EG=______.
32.下列三个说法:
①若直线在平面外,则;
②若直线,直线,则;
③若,则与内任意直线平行.
其中正确的有________.
33.以下命题中为真命题的是__________________(填序号)
①若直线平行于平面内的无数条直线,则直线∥;
②若直线在平面外,则∥;
③若直线a∥b,,则∥;
④若直线a∥b,,则平行于平面内的无数条直线.
34.如图所示,在空间四边形中,,分别为边,上的点,且,又,分别为,的中点,则下列结论正确的是__________________(请填写正确命题的序号)
①平面;②平面;
③平面;④平面.
四、解答题
35.如图,正方形ABCD与正方形ABEF所在平面相交于AB,在对角线AE,BD上各有一点P,Q,且AP=DQ.求证:平面BCE.(用两种方法证明)
36.如图,四棱锥中,O为底面平行四边形DBCE对角线的交点,F为AE的中点.求证:平面DCF.
37.如图,在三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2,若MB∥平面AEF,试判断点M在何位置.
38.如图,在直三棱柱中,点为的中点,,,.
(1)证明:平面.
(2)求三棱锥的体积.
39.如图1,已知矩形中,,E为上一点且.现将沿着折起,使点D到达点P的位置,且,得到的图形如图2.
(1)证明为直角三角形;
(2)设动点M在线段上,判断直线与平面的位置关系,并说明理由.
40.如图,E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,求证:
(1)四点E,F,G,H共面;
(2)平面,平面.
41.如图所示,斜三棱柱中,点为上的中点.
(1)求证:平面;
(2)设三棱锥的体积为,三棱柱的体积为,求.
【答案详解】
1.D
【解析】
【分析】
画出图形,当满足题目中的条件时,出现的情况有哪些,即可得出结论.
【详解】
解:如图,
;
当∠AOB=∠A1O1B1时,且OA∥O1A1,OA与O1A1的方向相同,
OB与O1B1是不一定平行.
故选:D.
2.证明见解析
【解析】
【分析】
证明,,由与的对应边平行且方向相同即可证出.
【详解】
因为为的中点,所以,因为为的中点,
所以.
又,,
所以,.所以四边形为平行四边形.
所以,同理.
所以与的对应边平行且方向相同,所以.
3.证明见解析
【解析】
【分析】
通过平行以及长度关系证明,,然后根据等角定理证明.
【详解】
证明:因为,分别是,的中点,所以,
所以四边形为平行四边形,所以.
同理可证,
又与方向相同,所以.
4.(1)证明见解析;(2)直线面,证明见解析.
【解析】
【分析】
(1)证明,利用线面平行的判定定理即可求证;
(2)由三角形中位线性质可得:,可证明面,由线面平行的性质定理可得,由线面平行的判定定理即可证明直线面.
【详解】
(1)因为分别为,的中点,所以,
因为底面是菱形,所以,所以,
因为平面,平面,
所以平面,
(2)直线与平面平行,证明如下:
因为分别为,的中点,
所以,
因为面,面,所以面,
因为平面与底面的交线为,面,
由线面平行的性质定理可得,
因为,所以,
因为面,面,
所以直线面.
5.(1)平面,证明见解析;(2),证明见解析.
【解析】
【分析】
(1)取PD中点E,连接AE,NE,可得,且,又M为AB中点,可得,且,所以四边形AMNE为平行四边形,可得,根据线面平行的判定定理,可证平面.
(2)根据线面平行的判定定理,可证平面,又平面PBC,结合题意,根据线面平行的性质定理,可证.
【详解】
(1)平面,证明如下:
取PD中点E,连接AE,NE,
因为N,E分别为PC,PD中点,
所以,且,
又M为AB中点,,,
所以,且,
所以四边形AMNE为平行四边形,
所以,
又平面,平面,
所以平面.
(2),证明如下:
因为,平面,平面,
所以平面,
又平面PBC,且平面平面,
根据线面平行的性质定理可得.
6.(1)见解析;(2)不平行,证明见解析
【解析】
【分析】
(1)可结合中位线定理证明,取PC的中点F,连接EF,BF,先证明四边形为平行四边形,可得,即可得证;
(2)可采用反证法,假设与平面平行,先证为中点,再通过相似三角形可得,即证出矛盾,故不成立
【详解】
证明:(1)取PC的中点F,连接EF,BF,
则,且,
又因为,,
所以,且,
所以四边形为平行四边形,
则,
又因为平面,平面,
所以平面.
(2)与平面不平行.
假设面,
设,连结,
则平面平面,
又平面, 所以.
所以,在中有,
由为的中点可得,即.
因为,所以,这与矛盾,
所以假设错误,与平面不平行.
【点睛】
本题考查线面平行的证明,反证法在线面平行中的应用,属于中档题
7.C
【解析】
【分析】
根据,得到,利用平面,得到,结合比例式的性质,得到,即可求解.
【详解】
解:设与交于点,连接,如图所示,因为为的中点,则,
由四边形是菱形,可得,则,
所以,所以,
又因为平面,平面,平面平面,
所以,所以.
故选:C.
8.C
【解析】
【分析】
连接,交于,连接,由平面,得到,由点,分别为棱,的中点,得到是的重心,由此能求出结果.
【详解】
解:连接,交于,连接,如图,
平面,平面平面,
,
点,分别为棱,的中点.
是的重心,
.
故选:C.
9.D
【解析】
【分析】
根据,得到,利用平面,得到,结合比例式的性质,得到,即可求解.
【详解】
设与交于点,连接,如图所示,
因为为的中点,则,
由四边形是平行四边形,可得,则,
所以,所以,
又因为平面,平面,平面平面,
所以,所以.
故选:D.
10.证明见解析
【解析】
【分析】
根据线面平行的判定定理、性质定理即可得证
【详解】
因为四边形EFGH为平行四边形,
所以,
因为平面BCD,平面BCD,
所以平面BCD,
又因为平面ACD,且平面平面BCD,
所以,
又因为平面EFGH,平面EFGH,
所以平面EFGH
11.(1)证明见解析;(2)证明见解析.
【解析】
【分析】
(1)先由BC∥AD证明BC∥平面PAD,再结合平面PBC∩平面PAD=l,由线面平行推出线线平行,即得证;
(2)取PD的中点E,连接AE,NE,可证明四边形AMNE是平行四边形,即 MN∥AE,由线线平行推线面平行,即得证
【详解】
(1)∵ ABCD
∴BC∥AD,
又BC平面PAD,平面PAD
∴BC∥平面PAD.
又∵平面PBC∩平面PAD=l,
平面PBC
∴l∥BC.
(2)如图,取PD的中点E,连接AE,NE,
则NE∥CD,且NE=CD,
又AM∥CD,且AM=CD,
∴NE∥AM,且NE=AM.
∴四边形AMNE是平行四边形.∴MN∥AE.
又∵AE 平面PAD,MN平面PAD,
∴MN∥平面PAD.
12.(1)证明见解析;(2)证明见解析;(3)存在;理由见解析.
【解析】
【分析】
(1)根据线面平行性质定理即可证明;
(2)取的中点,连接,,利用中位线的性质,平行四边形的性质,以及线面平行的判断定理即可证明;
(3)取中点,连接,,根据线面平行的性质定理和判断定理即可证明.
【详解】
证明:(1)在四棱锥中,平面,平面,
平面∩平面,
∴;
(2)取的中点,连接,,
∵是 的中点,
∴,,
又由(1)可得,,
∴,,
∴四边形是平行四边形,
∴,
∵平面,平面,
∴平面.
(3)取中点,连接,,
∵,分别为,的中点,
∴,
∵平面,平面,
∴平面,
又由(2)可得平面,,
∴ 平面平面,
∵是上的动点,平面,
∴平面,
∴ 线段上存在点,使平面.
【点睛】
本题考查线面平行、线线平行的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理能力,是中档题.
13.C
【解析】
【分析】
利用线面平行的判定定理和性质定理,结合空间图形构造反例,依次判断即可
【详解】
对于A,如图①,此时n与α相交,故选项A不正确;
对于B,如图②,此时m,n是异面直线,而n与α平行,故选项B不正确;
对于C,如果m α,nα,则mn或者m,n异面,又m,n共面,那么mn,故选项C正确
对于D,如图③,m与n相交,故选项D不正确.
故选:C
14.D
【解析】
【分析】
A,D选项考查线面平行的判断,A选项缺少条件,D选项正确;B选项是线面平行推线线平行,需要借助另外一个面;C选项中,平行于同一个面的两条线没有特定的位置关系
【详解】
选项A中,由推出平行于经过的任意一个平面,需要增加一个条件,即不在所在的面内,A选项没有这一限制条件,所以A错误
选项B中,,,,则,所以不是平行于面内所有的线,只能平行于面面的交线,所以B错误
选项C中,两条直线分别平行于面,这两条直线的位置关系是任意的,不能推出平行,所以C错误
选项D为证明线面平行的判定定理,条件充分,正确
故选:D
15.C
【解析】
【分析】
对选项A,B,D,借助长方体即可判断A,B,D错误,对选项C,利用线面平行的性质即可判断C正确.
【详解】
对选项A,如图所示:
在长方体中,满足,,此时,故A错误.
对选项B,如图所示:
在长方体中,满足,,此时相交,故B错误.
对选项C,根据线面平行的性质即可得到C正确.
对选项D,如图所示:
在长方体中,满足,,此时相交,故D错误.
故选:C
16.B
【解析】
根据PQMN是正方形,利用线面平行的判定定理、性质定理,即可判断A、C、D的正误,利用三角形相似及题干条件,即可判断B的正误,即可得答案.
【详解】
因为截面PQMN是正方形,
所以PQ∥MN,QM∥PN,
则PQ∥平面ACD,QM∥平面BDA,
所以PQ∥AC,QM∥BD,
由PQ⊥QM,可得AC⊥BD,故A正确;
由PQ∥AC,可得AC∥截面PQMN,故C正确;
由BD∥PN,所以∠MPN(或其补角)是异面直线PM与BD所成的角,
又PQMN是正方形,,故D正确;
由上面可知,BD∥PN,MN∥AC.
所以,
而AN≠DN,PN=MN,
所以BD≠AC,故B错误.
故选:B.
17.A
【解析】
连接交于,连接,根据线面平行的性质得,即可得到,即可求解.
【详解】
连接交于,连接,如图:
底面ABCD为菱形,Q为AD的中点,所以与相似,
,
因为平面MQB,平面,平面与平面MQB交线为,
根据线面平行的性质可知:,
在中,,
,
即.
故选:A
【点睛】
此题考查根据线面平行的性质得线线平行,根据平行关系求解线段的比例关系.
18.C
【解析】
根据三角形的中位线证得,由此证得平面,平面.根据与平面、平面有公共点,判断④⑤错误.
【详解】
矩形的对角线与交于点O,所以O为的中点,在中,M是的中点,所以是中位线,
故.又平面,平面,
所以平面,且平面.
因为点M在上,所以与平面、平面相交,所以④⑤错误.
故正确的结论为①②③,共有3个.
故选:C.
【点睛】
本小题主要考查线线平行、线面平行的证明,考查空间想象能力和逻辑推理能力,属于基础题.
19.B
【解析】
【分析】
根据空间中直线间的位置关系逐项进行判断即可.
【详解】
①错误,两条直线可以异面;
②正确,平行的传递性;
③错误,和另一条直线可以相交也可以异面;
④正确,平行的传递性.
故选:B.
20.A
【解析】
利用平面的公理直接判断求解.
【详解】
不是公理,
在中,由公理三知:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线,故是公理.
在中,由公理一知:如果一条直线上的两点在一个平面内,那么这条直线在此平面内,故是公理;
在中,由平行公理得:平行于同一条直线的两条直线互相平行,故是公理;
故选:.
【点睛】
本题考查平面的公理的判断,考查平面的基本性质及其推论等基础知识,是基础题.
21.B
【解析】
【分析】
先判断四边形EFGH的形状,再去判断线面是否平行即可解决.
【详解】
△ABD中,AE∶EB=AF∶FD=1∶4,则EFBD,且
△BCD中,,则HGBD,且
则,则四边形EFGH是梯形.故选B.
下面看四个平行的判断是否正确.
平面,平面,则BD平面EFGH.判断正确;
平面,平面,则EF平面BCD.判断正确;
平面,平面,则HG平面ABD.判断正确;
梯形EFGH中,,与的延长线会交于一点,则直线EH与平面ADC的位置关系为相交.
故选:B
22.B
【解析】
【分析】
根据异面直线的判定定理,直线与平面平行的判定定理,四点共面的判定,结合四棱柱的性质逐一判定即可.
【详解】
面,面,,所以与是异面直线,A错;
因为,面,面,所以面,B正确;
面, 面,,所以与是异面直线,C错;
如图所示,,,三点在面上,与面相交,所以,,,四点不共面,D错.
故选:B.
23.A
【解析】
【分析】
由,可推出,再根据线面平行的判定可得出答案.
【详解】
∵
∴
又∵,.
∴平面.
故选:A
24.B
【解析】
【分析】
证明,即可证明②③正确;平面,故①错误,平面,故④错误.
【详解】
对于①,平面,故①错误;
对于②,由于为的中点,为的中点,则, 平面,平面,则平面,故②正确;
对于③,由于,平面,平面,则平面,故③正确;
对于④,由于平面,故④错误.
故选:B
25.AC
【解析】
【分析】
由等角定理可判断A、B的真假;举反例可判断C的真假;由平行公理可判断D的真假.
【详解】
对于选项A:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补,故选项A错误;
对于选项B:由等角定理可知B正确;
对于选项C:如果一个角的两边和另一个角的两边分别垂直,这两个角的关系不确定,既可能相等也可能互补,也可能既不相等,也不互补.反例如图,在立方体中,与满足,,但是,,二者不相等也不互补.故选项C错误;
对于选项D:如果两条直线同时平行于第三条直线,那么这两条直线平行,故选项D正确.
故选:AC.
26.AB
【解析】
【分析】
根据图形及题目中的条件进行判断即可.
【详解】
由题意知: ,,,所以,故A正确;
由,平面,平面,故平面.
故选:AB.
27.BD
【解析】
【分析】
取的中点,连接,,可得,由与相交判定A错误;连接,由面面平行的判定及性质判断B;利用等体积法求体积判断C;求出点的轨迹判断D.
【详解】
对于A,取的中点,连接,,由正方体的性质可知,
而与相交,故与不平行,故A错误;
对于B,连接,因为,平面,平面
所以平面,同理平面,因为
所以平面平面,因为平面
所以平面,故B正确;
对于C,由等体积法可得:
,故C错误;
对于D,由前面可得平面平面,即点的轨迹为线段,故D正确.
故选:BD
28.BC
【解析】
【分析】
根据正方体的性质一一判断即可;
【详解】
解:在正方体中,则与不垂直,从而直线与直线不垂直,故A错误;
取的中点,连接、,则,,易证平面平面,从而直线与平面平行,故B正确;
连接,,,因为,,所以,故四边形为平面截正方体的截面,显然四边形为等腰梯形,故C正确;
假设点与点到平面的距离相等,即平面平分,则平面必过的中点,连接交于点,易知不是的中点,故假设不成立,故D错误;
故选:BC
29.ACD
【解析】
【分析】
由旋转前后底面平行,几何体高不变,底面边长不变,外接球不变依次判断即可.
【详解】
由,可得平面ABC,所以A正确.;
作平面,垂足为 ,连结、,则,
所以,所以B错;
由A、B选项的上述判断过程可知四边形为菱形,
又平面,所以,
故四边形为正方形,C正确;
因为旋转前与旋转后几何体的外接球不变,故D正确.
故选: ACD.
30.③
【解析】
【分析】
①利用平面的位置关系判断;②利用直线与直线的位置关系判断;③利用线面平行的性质定理判断.
【详解】
①若l与m为异面直线,l α,m β,则αβ或α与β相交;
②若αβ,l α,m β,则lm或直线l与m异面;
③因为α∩β=l,β∩γ=m, lγ,所以ml,同理可证ln,所以mn.
故答案为:③
31.##
【解析】
【分析】
利用线面平行的性质可得∥,然后利用平行线分线段成比例定理和比例的性质求解
【详解】
因为直线平面,点B,C,,平面平面,
所以∥,
所以,
所以,
故答案为:
32.②
【解析】
【分析】
由线面的位置关系可判断①,利用线面平行的判定定理可判断②,再利用线线的位置关系判断③.
【详解】
直线在平面外,包含直线与相交、直线与平行两种情况,①不正确;
由直线与平面平行的判定定理知②正确;
③中与内的直线可能平行,相交、异面,③不正确.
故答案为:②
33.④
【解析】
【分析】
利用线面平行的判定定理及性质分析判断即可
【详解】
对于①,当直线平行于平面内的无数条直线时,∥或在平面内,所以①错误,
对于②,直线在平面外,则∥或与平面相交,所以②错误,
对于③,若直线a∥b,,则∥或在平面内,所以③错误,
对于④,若直线a∥b,,则由线面平行的性质可得平行于平面内的无数条直线,所以④正确,
故答案为:④
34.①②③
【解析】
【分析】
根据题意,,,进而根据线面平行的判定定理即可得答案.
【详解】
解:∵ 在中,,
∴,
又∵ 平面,平面,平面,平面
∴ 平面;平面;
∵,分别为,的中点,
∴ ,
又∵平面,平面,
∴ 平面
∴,
∴ 四边形是梯形,
∴与必相交,
∵平面,
∴与平面有公共点,即与平面不平行.
综上,正确的是:①②③
故答案为:①②③
35.见解析
【解析】
【分析】
作交于,作交于,连接,证明出四边形为平行四边形,可得出,利用线面平行的判定定理可证得结论成立.
【详解】
法一:如图所示,交于,作交于,连接.
正方形和正方形有公共边,.
又,.
又,,,.
且,即四边形为平行四边形,.
又平面,平面,平面.
法二:如图所示,连接并延长交所在直线与点,连接,
由可得,,
因为正方形和正方形有公共边,所以,
又,则,
所以,所以,
又平面,平面,平面.
36.证明见解析
【解析】
【分析】
以线面平行判定定理去证明即可.
【详解】
连接OF
O为底面平行四边形DBCE对角线的交点,则
△中,,,则
又平面,平面,则平面DCF.
37.M是AC的中点
【解析】
【分析】
根据线面平行的性质、平行四边形的定义、平行四边形的性质,结合三角形中位线的性质进行求解即可.
【详解】
解 若MB∥平面AEF,过F,B,M作平面FBMN交AE于点N,
连接MN,NF.
因为BF∥平面AA1C1C,
BF 平面FBMN,
平面FBMN∩平面AA1C1C=MN,
所以BF∥MN.
又MB∥平面AEF,MB 平面FBMN,
平面FBMN∩平面AEF=FN,所以MB∥FN,
所以BFNM是平行四边形,
所以MN∥BF,MN=BF=1.
而EC∥FB,EC=2FB=2,
所以MN∥EC,MN=EC=1,
故MN是△ACE的中位线.
所以当M是AC的中点时,
MB∥平面AEF.
38.(1)证明见解析
(2)
【解析】
【分析】
(1)在平面内作出辅助线,然后根据线面平行的判定定理证明即可;
(2)作出三棱锥的高,将看作三棱锥的底面,利用三棱锥体积公式计算即可.
(1)
证明:连接,交于,连接,因为是直三棱柱,所以为中点,而点为的中点,
所以,
因为平面,平面,
所以平面.
(2)
解:过作于,
因为是直三棱柱,点为的中点,
所以,且底面,
所以,
因为,所以,
则 ,
所以
.
39.(1)证明见解析
(2)答案不唯一,见解析
【解析】
【分析】
(1)利用折叠前后的线段长度及勾股定理求证即可;
(2)动点M满足时和,但时两种情况,利用线线平行或相交得到结论.
(1)
在折叠前的图中,如图:
,E为上一点且,
则,
折叠后,所以,又,
所以,所以为直角三角形.
(2)
当动点M在线段上,满足,同样在线段上取,使得,则,
当时,则,又且所以,且,
所以四边形为平行四边形,所以,又平面,所以此时平面;
当时,此时,但,
所以四边形为梯形,所以与必然相交,所以与平面必然相交.
综上,当动点M满足时,平面;
当动点M满足,但时,与平面相交.
40.(1)证明见解析;
(2)证明见解析.
【解析】
【分析】
(1)证明即可证明结论
(2)根据线面平行的判定定理证明即可.
(1)
证明:因为E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,
所以,
所以,
所以四点E,F,G,H共面.
(2)
证明:因为E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,
所以,
因为平面,平面,平面,平面,
所以平面, 平面
41.(1)证明见解析;(2).
【解析】
【分析】
(1)连接A1B交AB1于点O,连接OD1,可得OD1∥BC1,由线面平行的判定定理即可证明BC1∥平面AB1D1;
(2)由V1====V2,即可求得结论.
【详解】
(1)证明:连接A1B交AB1于点O,连接OD1,
则在平形四边形ABB1A1中,点O为A1B的中点,
又点D1为A1C1的中点,
所以OD1∥BC1,
又OD1 平面AB1D1,B1C 平面AB1D1,
所以BC1∥平面AB1D1.
(2)V1====V2
所以=.
试卷第1页,共3页
【考点梳理】
考点一 基本事实4
文字语言 平行于同一条直线的两条直线平行
图形语言
符号语言 直线a,b,c,a∥b,b∥c a∥c
作用 证明两条直线平行
说明 基本事实4表述的性质通常叫做平行线的传递性
考点二 空间等角定理
1.定理
文字语言 如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补
符号语言 OA∥O′A′,OB∥O′B′ ∠AOB=∠A′O′B′或∠AOB+∠A′O′B′=180°
图形语言
作用 判断或证明两个角相等或互补
2.推广
如果两条相交直线与另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.
考点三 直线与平面平行的判定定理
文字语言 如果平面外一条直线与此平面内一条直线平行,那么该直线与此平面平行
符号语言 a∥α
图形语言
考点四 直线与平面平行的性质定理
文字语言 一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行
符号语言 a∥α,a β,α∩β=b a∥b
图形语言
【题型归纳】
题型一:等角定理
1.若,且,与方向相同,则下列结论正确的有( )
A.且方向相同 B.,方向可能不同
C.OB与不平行 D.OB与不一定平行
2.在正方体中,,,分别为棱,,的中点,试证明:.
3.如图,三棱柱中,,,分别为,,的中点.求证:.
题型二:直线与平面平行的判定定理的应用
4.如图,在四棱锥中,底面是菱形,分别为,,的中点.
(1)求证:平面;
(2)记平面与底面的交线为,试判断直线与平面的位置关系,并证明.
5.如图,P为平行四边形所在平面外一点,,分别是,的中点,平面平面于直线.
(1)判断与平面的位置关系,并证明你的结论;
(2)判断与的位置关系,并证明你的结论.
6.如图,在四棱锥中,,,为棱的中点.
(1)求证:平面;
(2)试判断与平面是否平行?并说明理由.
题型三:直线与平面平行的性质判断线段比例或点所在位置
7.如图,已知四棱锥的底面是菱形,交于点O,E为的中点,F在上,,∥平面,则的值为( )
A.1 B. C.3 D.2
8.如图,在三棱锥P—ABC中,点D,E分别为棱PB,BC的中点.若点F在线段AC上,且满足AD平面PEF,则的值为( )
A.1 B.2 C. D.
9.如图,已知四棱维的底面是平行四边形,交于点,为中点,在上,,平面,则的值为( )
A. B. C. D.
题型四:直线与平面平行的性质定理的应用
10.如图,三棱锥被一平面所截,截面为平行四边形EFGH,求证:平面EFGH.
11.如图所示,已知P是 ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.
求证:(1)l∥BC;
(2)MN∥平面PAD.
12.如图所示,在四棱锥中,平面,,是的中点.
(1)求证:;
(2)求证:平面;
(3)若是线段上一动点,则线段上是否存在点,使平面?说明理由.
【双基达标】
一、单选题
13.对于直线m,n和平面α,下列命题中正确的是( )
A.如果m α,nα,m,n是异面直线,那么nα
B.如果m α,nα,m,n是异面直线,那么n与α相交
C.如果m α,nα,m,n共面,那么mn
D.如果mα,nα,m,n共面,那么mn
14.已知直线和平面,下列说法正确的是( )
A.如果,那么平行于经过的任意一个平面.
B.如果,那么平行于平面内的任意一条直线.
C.若,则 .
D.若且,则.
15.已知m,n为两条不同的直线,,为两个不同的平面,则下列结论中正确的是( )
A.若,,则
B.若,n,则
C.若,m,=n,则
D.若,,则
16.如图,在四面体ABCD中,若截面PQMN是正方形,则在下列说法中,错误的为( )
A.AC⊥BD B.AC=BD C.AC∥截面PQMN D.异面直线PM与BD所成的角为45°
17.如图,在四棱锥中,底面ABCD为菱形,,Q为AD的中点,点M在线段PC上,,若平面MQB,则t等于( )
A. B. C. D.
18.如图所示,P为矩形所在平面外一点,矩形对角线交点为为的中点,给出五个结论:①;②平面;③平面;④平面;⑤平面.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
19.下列结论中正确的是( )
①在空间中,若两条直线不相交,则它们一定平行;②平行于同一条直线的两条直线平行;③一条直线和两条平行直线中的一条相交,那么它也和另一条相交;④空间中有四条直线a,b,c,d,如果ab,cd,且ad,那么bc.
A.①②③ B.②④ C.③④ D.②③
20.下列命题的符号语言中,不是公理的是( )
A.,
B.,且,且
C.,,且,
D.,
21.如图所示,在空间四边形ABCD中,E,F分别为边AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则( )
A.BD平面EFGH,且四边形EFGH是矩形
B.EF平面BCD,且四边形EFGH是梯形
C.HG平面ABD,且四边形EFGH是菱形
D.EH平面ADC,且四边形EFGH是平行四边形
【高分突破】
一:单选题
22.如图,在直四棱柱中,下列结论正确的是( )
A.与是两条相交直线
B.平面
C.
D.,,,四点共面
23.在空间四边形中,分别在上,且满足,则直线与平面的位置关系是( )
A.平面 B.平面
C.与平面相交 D.以上都有可能
24.如图所示,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,下列结论正确的个数为( )
①平面PBC ②平面PCD ③平面PDA ④平面PBA
A.1个 B.2个 C.3个 D.4个
二、多选题
25.(多选题)下列命题中,错误的结论有( )
A.如果一个角的两边与另一个角的两边分别平行,那么这两个角相等
B.如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等
C.如果一个角的两边和另一个角的两边分别垂直,那么这两个角相等或互补
D.如果两条直线同时平行于第三条直线,那么这两条直线互相平行
26.如图,在四面体中,截面是正方形,则( )
A. B.平面
C. D.分别是线段的中点
27.如图所示,在棱长为2的正方体中,,,分别为所在棱的中点,为正方形内(包括边界)一动点,且平面,则( )
A. B.平面
C.三棱锥的体积为1 D.只能在线段上
28.在正方体中,、、分别为,,的中点则( )
A.直线与直线垂直
B.直线与平面平行
C.平面截正方体所得的截而是等腰梯形
D.点和点到平面的距离相等
29.已知图1中的正三棱柱的底面边长为2,体积为,去掉其侧棱,再将上底面绕上下底面的中心所在的直线,逆时针旋转后,添上侧棱,得到图2所示的几何体,则下列说法正确的是( )
图1 图2
A.平面ABC
B.
C.四边形为正方形
D.正三棱柱,与几何体的外接球体积相同
三、填空题
30.已知l,m,n是互不相同的直线,α,β,γ是三个不同的平面,给出下列命题:
①若l与m为异面直线,l α,m β,则αβ;
②若αβ,l α,m β,则lm;
③若α∩β=l,β∩γ=m,γ∩α=n,lγ,则mn.
其中所有真命题的序号为________.
31.如图所示,直线平面,点平面,并且直线a和点A位于平面两侧,点B,C,,AB,AC,AD分别交平面于点E,F,G,若,,,则EG=______.
32.下列三个说法:
①若直线在平面外,则;
②若直线,直线,则;
③若,则与内任意直线平行.
其中正确的有________.
33.以下命题中为真命题的是__________________(填序号)
①若直线平行于平面内的无数条直线,则直线∥;
②若直线在平面外,则∥;
③若直线a∥b,,则∥;
④若直线a∥b,,则平行于平面内的无数条直线.
34.如图所示,在空间四边形中,,分别为边,上的点,且,又,分别为,的中点,则下列结论正确的是__________________(请填写正确命题的序号)
①平面;②平面;
③平面;④平面.
四、解答题
35.如图,正方形ABCD与正方形ABEF所在平面相交于AB,在对角线AE,BD上各有一点P,Q,且AP=DQ.求证:平面BCE.(用两种方法证明)
36.如图,四棱锥中,O为底面平行四边形DBCE对角线的交点,F为AE的中点.求证:平面DCF.
37.如图,在三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2,若MB∥平面AEF,试判断点M在何位置.
38.如图,在直三棱柱中,点为的中点,,,.
(1)证明:平面.
(2)求三棱锥的体积.
39.如图1,已知矩形中,,E为上一点且.现将沿着折起,使点D到达点P的位置,且,得到的图形如图2.
(1)证明为直角三角形;
(2)设动点M在线段上,判断直线与平面的位置关系,并说明理由.
40.如图,E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,求证:
(1)四点E,F,G,H共面;
(2)平面,平面.
41.如图所示,斜三棱柱中,点为上的中点.
(1)求证:平面;
(2)设三棱锥的体积为,三棱柱的体积为,求.
【答案详解】
1.D
【解析】
【分析】
画出图形,当满足题目中的条件时,出现的情况有哪些,即可得出结论.
【详解】
解:如图,
;
当∠AOB=∠A1O1B1时,且OA∥O1A1,OA与O1A1的方向相同,
OB与O1B1是不一定平行.
故选:D.
2.证明见解析
【解析】
【分析】
证明,,由与的对应边平行且方向相同即可证出.
【详解】
因为为的中点,所以,因为为的中点,
所以.
又,,
所以,.所以四边形为平行四边形.
所以,同理.
所以与的对应边平行且方向相同,所以.
3.证明见解析
【解析】
【分析】
通过平行以及长度关系证明,,然后根据等角定理证明.
【详解】
证明:因为,分别是,的中点,所以,
所以四边形为平行四边形,所以.
同理可证,
又与方向相同,所以.
4.(1)证明见解析;(2)直线面,证明见解析.
【解析】
【分析】
(1)证明,利用线面平行的判定定理即可求证;
(2)由三角形中位线性质可得:,可证明面,由线面平行的性质定理可得,由线面平行的判定定理即可证明直线面.
【详解】
(1)因为分别为,的中点,所以,
因为底面是菱形,所以,所以,
因为平面,平面,
所以平面,
(2)直线与平面平行,证明如下:
因为分别为,的中点,
所以,
因为面,面,所以面,
因为平面与底面的交线为,面,
由线面平行的性质定理可得,
因为,所以,
因为面,面,
所以直线面.
5.(1)平面,证明见解析;(2),证明见解析.
【解析】
【分析】
(1)取PD中点E,连接AE,NE,可得,且,又M为AB中点,可得,且,所以四边形AMNE为平行四边形,可得,根据线面平行的判定定理,可证平面.
(2)根据线面平行的判定定理,可证平面,又平面PBC,结合题意,根据线面平行的性质定理,可证.
【详解】
(1)平面,证明如下:
取PD中点E,连接AE,NE,
因为N,E分别为PC,PD中点,
所以,且,
又M为AB中点,,,
所以,且,
所以四边形AMNE为平行四边形,
所以,
又平面,平面,
所以平面.
(2),证明如下:
因为,平面,平面,
所以平面,
又平面PBC,且平面平面,
根据线面平行的性质定理可得.
6.(1)见解析;(2)不平行,证明见解析
【解析】
【分析】
(1)可结合中位线定理证明,取PC的中点F,连接EF,BF,先证明四边形为平行四边形,可得,即可得证;
(2)可采用反证法,假设与平面平行,先证为中点,再通过相似三角形可得,即证出矛盾,故不成立
【详解】
证明:(1)取PC的中点F,连接EF,BF,
则,且,
又因为,,
所以,且,
所以四边形为平行四边形,
则,
又因为平面,平面,
所以平面.
(2)与平面不平行.
假设面,
设,连结,
则平面平面,
又平面, 所以.
所以,在中有,
由为的中点可得,即.
因为,所以,这与矛盾,
所以假设错误,与平面不平行.
【点睛】
本题考查线面平行的证明,反证法在线面平行中的应用,属于中档题
7.C
【解析】
【分析】
根据,得到,利用平面,得到,结合比例式的性质,得到,即可求解.
【详解】
解:设与交于点,连接,如图所示,因为为的中点,则,
由四边形是菱形,可得,则,
所以,所以,
又因为平面,平面,平面平面,
所以,所以.
故选:C.
8.C
【解析】
【分析】
连接,交于,连接,由平面,得到,由点,分别为棱,的中点,得到是的重心,由此能求出结果.
【详解】
解:连接,交于,连接,如图,
平面,平面平面,
,
点,分别为棱,的中点.
是的重心,
.
故选:C.
9.D
【解析】
【分析】
根据,得到,利用平面,得到,结合比例式的性质,得到,即可求解.
【详解】
设与交于点,连接,如图所示,
因为为的中点,则,
由四边形是平行四边形,可得,则,
所以,所以,
又因为平面,平面,平面平面,
所以,所以.
故选:D.
10.证明见解析
【解析】
【分析】
根据线面平行的判定定理、性质定理即可得证
【详解】
因为四边形EFGH为平行四边形,
所以,
因为平面BCD,平面BCD,
所以平面BCD,
又因为平面ACD,且平面平面BCD,
所以,
又因为平面EFGH,平面EFGH,
所以平面EFGH
11.(1)证明见解析;(2)证明见解析.
【解析】
【分析】
(1)先由BC∥AD证明BC∥平面PAD,再结合平面PBC∩平面PAD=l,由线面平行推出线线平行,即得证;
(2)取PD的中点E,连接AE,NE,可证明四边形AMNE是平行四边形,即 MN∥AE,由线线平行推线面平行,即得证
【详解】
(1)∵ ABCD
∴BC∥AD,
又BC平面PAD,平面PAD
∴BC∥平面PAD.
又∵平面PBC∩平面PAD=l,
平面PBC
∴l∥BC.
(2)如图,取PD的中点E,连接AE,NE,
则NE∥CD,且NE=CD,
又AM∥CD,且AM=CD,
∴NE∥AM,且NE=AM.
∴四边形AMNE是平行四边形.∴MN∥AE.
又∵AE 平面PAD,MN平面PAD,
∴MN∥平面PAD.
12.(1)证明见解析;(2)证明见解析;(3)存在;理由见解析.
【解析】
【分析】
(1)根据线面平行性质定理即可证明;
(2)取的中点,连接,,利用中位线的性质,平行四边形的性质,以及线面平行的判断定理即可证明;
(3)取中点,连接,,根据线面平行的性质定理和判断定理即可证明.
【详解】
证明:(1)在四棱锥中,平面,平面,
平面∩平面,
∴;
(2)取的中点,连接,,
∵是 的中点,
∴,,
又由(1)可得,,
∴,,
∴四边形是平行四边形,
∴,
∵平面,平面,
∴平面.
(3)取中点,连接,,
∵,分别为,的中点,
∴,
∵平面,平面,
∴平面,
又由(2)可得平面,,
∴ 平面平面,
∵是上的动点,平面,
∴平面,
∴ 线段上存在点,使平面.
【点睛】
本题考查线面平行、线线平行的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理能力,是中档题.
13.C
【解析】
【分析】
利用线面平行的判定定理和性质定理,结合空间图形构造反例,依次判断即可
【详解】
对于A,如图①,此时n与α相交,故选项A不正确;
对于B,如图②,此时m,n是异面直线,而n与α平行,故选项B不正确;
对于C,如果m α,nα,则mn或者m,n异面,又m,n共面,那么mn,故选项C正确
对于D,如图③,m与n相交,故选项D不正确.
故选:C
14.D
【解析】
【分析】
A,D选项考查线面平行的判断,A选项缺少条件,D选项正确;B选项是线面平行推线线平行,需要借助另外一个面;C选项中,平行于同一个面的两条线没有特定的位置关系
【详解】
选项A中,由推出平行于经过的任意一个平面,需要增加一个条件,即不在所在的面内,A选项没有这一限制条件,所以A错误
选项B中,,,,则,所以不是平行于面内所有的线,只能平行于面面的交线,所以B错误
选项C中,两条直线分别平行于面,这两条直线的位置关系是任意的,不能推出平行,所以C错误
选项D为证明线面平行的判定定理,条件充分,正确
故选:D
15.C
【解析】
【分析】
对选项A,B,D,借助长方体即可判断A,B,D错误,对选项C,利用线面平行的性质即可判断C正确.
【详解】
对选项A,如图所示:
在长方体中,满足,,此时,故A错误.
对选项B,如图所示:
在长方体中,满足,,此时相交,故B错误.
对选项C,根据线面平行的性质即可得到C正确.
对选项D,如图所示:
在长方体中,满足,,此时相交,故D错误.
故选:C
16.B
【解析】
根据PQMN是正方形,利用线面平行的判定定理、性质定理,即可判断A、C、D的正误,利用三角形相似及题干条件,即可判断B的正误,即可得答案.
【详解】
因为截面PQMN是正方形,
所以PQ∥MN,QM∥PN,
则PQ∥平面ACD,QM∥平面BDA,
所以PQ∥AC,QM∥BD,
由PQ⊥QM,可得AC⊥BD,故A正确;
由PQ∥AC,可得AC∥截面PQMN,故C正确;
由BD∥PN,所以∠MPN(或其补角)是异面直线PM与BD所成的角,
又PQMN是正方形,,故D正确;
由上面可知,BD∥PN,MN∥AC.
所以,
而AN≠DN,PN=MN,
所以BD≠AC,故B错误.
故选:B.
17.A
【解析】
连接交于,连接,根据线面平行的性质得,即可得到,即可求解.
【详解】
连接交于,连接,如图:
底面ABCD为菱形,Q为AD的中点,所以与相似,
,
因为平面MQB,平面,平面与平面MQB交线为,
根据线面平行的性质可知:,
在中,,
,
即.
故选:A
【点睛】
此题考查根据线面平行的性质得线线平行,根据平行关系求解线段的比例关系.
18.C
【解析】
根据三角形的中位线证得,由此证得平面,平面.根据与平面、平面有公共点,判断④⑤错误.
【详解】
矩形的对角线与交于点O,所以O为的中点,在中,M是的中点,所以是中位线,
故.又平面,平面,
所以平面,且平面.
因为点M在上,所以与平面、平面相交,所以④⑤错误.
故正确的结论为①②③,共有3个.
故选:C.
【点睛】
本小题主要考查线线平行、线面平行的证明,考查空间想象能力和逻辑推理能力,属于基础题.
19.B
【解析】
【分析】
根据空间中直线间的位置关系逐项进行判断即可.
【详解】
①错误,两条直线可以异面;
②正确,平行的传递性;
③错误,和另一条直线可以相交也可以异面;
④正确,平行的传递性.
故选:B.
20.A
【解析】
利用平面的公理直接判断求解.
【详解】
不是公理,
在中,由公理三知:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线,故是公理.
在中,由公理一知:如果一条直线上的两点在一个平面内,那么这条直线在此平面内,故是公理;
在中,由平行公理得:平行于同一条直线的两条直线互相平行,故是公理;
故选:.
【点睛】
本题考查平面的公理的判断,考查平面的基本性质及其推论等基础知识,是基础题.
21.B
【解析】
【分析】
先判断四边形EFGH的形状,再去判断线面是否平行即可解决.
【详解】
△ABD中,AE∶EB=AF∶FD=1∶4,则EFBD,且
△BCD中,,则HGBD,且
则,则四边形EFGH是梯形.故选B.
下面看四个平行的判断是否正确.
平面,平面,则BD平面EFGH.判断正确;
平面,平面,则EF平面BCD.判断正确;
平面,平面,则HG平面ABD.判断正确;
梯形EFGH中,,与的延长线会交于一点,则直线EH与平面ADC的位置关系为相交.
故选:B
22.B
【解析】
【分析】
根据异面直线的判定定理,直线与平面平行的判定定理,四点共面的判定,结合四棱柱的性质逐一判定即可.
【详解】
面,面,,所以与是异面直线,A错;
因为,面,面,所以面,B正确;
面, 面,,所以与是异面直线,C错;
如图所示,,,三点在面上,与面相交,所以,,,四点不共面,D错.
故选:B.
23.A
【解析】
【分析】
由,可推出,再根据线面平行的判定可得出答案.
【详解】
∵
∴
又∵,.
∴平面.
故选:A
24.B
【解析】
【分析】
证明,即可证明②③正确;平面,故①错误,平面,故④错误.
【详解】
对于①,平面,故①错误;
对于②,由于为的中点,为的中点,则, 平面,平面,则平面,故②正确;
对于③,由于,平面,平面,则平面,故③正确;
对于④,由于平面,故④错误.
故选:B
25.AC
【解析】
【分析】
由等角定理可判断A、B的真假;举反例可判断C的真假;由平行公理可判断D的真假.
【详解】
对于选项A:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补,故选项A错误;
对于选项B:由等角定理可知B正确;
对于选项C:如果一个角的两边和另一个角的两边分别垂直,这两个角的关系不确定,既可能相等也可能互补,也可能既不相等,也不互补.反例如图,在立方体中,与满足,,但是,,二者不相等也不互补.故选项C错误;
对于选项D:如果两条直线同时平行于第三条直线,那么这两条直线平行,故选项D正确.
故选:AC.
26.AB
【解析】
【分析】
根据图形及题目中的条件进行判断即可.
【详解】
由题意知: ,,,所以,故A正确;
由,平面,平面,故平面.
故选:AB.
27.BD
【解析】
【分析】
取的中点,连接,,可得,由与相交判定A错误;连接,由面面平行的判定及性质判断B;利用等体积法求体积判断C;求出点的轨迹判断D.
【详解】
对于A,取的中点,连接,,由正方体的性质可知,
而与相交,故与不平行,故A错误;
对于B,连接,因为,平面,平面
所以平面,同理平面,因为
所以平面平面,因为平面
所以平面,故B正确;
对于C,由等体积法可得:
,故C错误;
对于D,由前面可得平面平面,即点的轨迹为线段,故D正确.
故选:BD
28.BC
【解析】
【分析】
根据正方体的性质一一判断即可;
【详解】
解:在正方体中,则与不垂直,从而直线与直线不垂直,故A错误;
取的中点,连接、,则,,易证平面平面,从而直线与平面平行,故B正确;
连接,,,因为,,所以,故四边形为平面截正方体的截面,显然四边形为等腰梯形,故C正确;
假设点与点到平面的距离相等,即平面平分,则平面必过的中点,连接交于点,易知不是的中点,故假设不成立,故D错误;
故选:BC
29.ACD
【解析】
【分析】
由旋转前后底面平行,几何体高不变,底面边长不变,外接球不变依次判断即可.
【详解】
由,可得平面ABC,所以A正确.;
作平面,垂足为 ,连结、,则,
所以,所以B错;
由A、B选项的上述判断过程可知四边形为菱形,
又平面,所以,
故四边形为正方形,C正确;
因为旋转前与旋转后几何体的外接球不变,故D正确.
故选: ACD.
30.③
【解析】
【分析】
①利用平面的位置关系判断;②利用直线与直线的位置关系判断;③利用线面平行的性质定理判断.
【详解】
①若l与m为异面直线,l α,m β,则αβ或α与β相交;
②若αβ,l α,m β,则lm或直线l与m异面;
③因为α∩β=l,β∩γ=m, lγ,所以ml,同理可证ln,所以mn.
故答案为:③
31.##
【解析】
【分析】
利用线面平行的性质可得∥,然后利用平行线分线段成比例定理和比例的性质求解
【详解】
因为直线平面,点B,C,,平面平面,
所以∥,
所以,
所以,
故答案为:
32.②
【解析】
【分析】
由线面的位置关系可判断①,利用线面平行的判定定理可判断②,再利用线线的位置关系判断③.
【详解】
直线在平面外,包含直线与相交、直线与平行两种情况,①不正确;
由直线与平面平行的判定定理知②正确;
③中与内的直线可能平行,相交、异面,③不正确.
故答案为:②
33.④
【解析】
【分析】
利用线面平行的判定定理及性质分析判断即可
【详解】
对于①,当直线平行于平面内的无数条直线时,∥或在平面内,所以①错误,
对于②,直线在平面外,则∥或与平面相交,所以②错误,
对于③,若直线a∥b,,则∥或在平面内,所以③错误,
对于④,若直线a∥b,,则由线面平行的性质可得平行于平面内的无数条直线,所以④正确,
故答案为:④
34.①②③
【解析】
【分析】
根据题意,,,进而根据线面平行的判定定理即可得答案.
【详解】
解:∵ 在中,,
∴,
又∵ 平面,平面,平面,平面
∴ 平面;平面;
∵,分别为,的中点,
∴ ,
又∵平面,平面,
∴ 平面
∴,
∴ 四边形是梯形,
∴与必相交,
∵平面,
∴与平面有公共点,即与平面不平行.
综上,正确的是:①②③
故答案为:①②③
35.见解析
【解析】
【分析】
作交于,作交于,连接,证明出四边形为平行四边形,可得出,利用线面平行的判定定理可证得结论成立.
【详解】
法一:如图所示,交于,作交于,连接.
正方形和正方形有公共边,.
又,.
又,,,.
且,即四边形为平行四边形,.
又平面,平面,平面.
法二:如图所示,连接并延长交所在直线与点,连接,
由可得,,
因为正方形和正方形有公共边,所以,
又,则,
所以,所以,
又平面,平面,平面.
36.证明见解析
【解析】
【分析】
以线面平行判定定理去证明即可.
【详解】
连接OF
O为底面平行四边形DBCE对角线的交点,则
△中,,,则
又平面,平面,则平面DCF.
37.M是AC的中点
【解析】
【分析】
根据线面平行的性质、平行四边形的定义、平行四边形的性质,结合三角形中位线的性质进行求解即可.
【详解】
解 若MB∥平面AEF,过F,B,M作平面FBMN交AE于点N,
连接MN,NF.
因为BF∥平面AA1C1C,
BF 平面FBMN,
平面FBMN∩平面AA1C1C=MN,
所以BF∥MN.
又MB∥平面AEF,MB 平面FBMN,
平面FBMN∩平面AEF=FN,所以MB∥FN,
所以BFNM是平行四边形,
所以MN∥BF,MN=BF=1.
而EC∥FB,EC=2FB=2,
所以MN∥EC,MN=EC=1,
故MN是△ACE的中位线.
所以当M是AC的中点时,
MB∥平面AEF.
38.(1)证明见解析
(2)
【解析】
【分析】
(1)在平面内作出辅助线,然后根据线面平行的判定定理证明即可;
(2)作出三棱锥的高,将看作三棱锥的底面,利用三棱锥体积公式计算即可.
(1)
证明:连接,交于,连接,因为是直三棱柱,所以为中点,而点为的中点,
所以,
因为平面,平面,
所以平面.
(2)
解:过作于,
因为是直三棱柱,点为的中点,
所以,且底面,
所以,
因为,所以,
则 ,
所以
.
39.(1)证明见解析
(2)答案不唯一,见解析
【解析】
【分析】
(1)利用折叠前后的线段长度及勾股定理求证即可;
(2)动点M满足时和,但时两种情况,利用线线平行或相交得到结论.
(1)
在折叠前的图中,如图:
,E为上一点且,
则,
折叠后,所以,又,
所以,所以为直角三角形.
(2)
当动点M在线段上,满足,同样在线段上取,使得,则,
当时,则,又且所以,且,
所以四边形为平行四边形,所以,又平面,所以此时平面;
当时,此时,但,
所以四边形为梯形,所以与必然相交,所以与平面必然相交.
综上,当动点M满足时,平面;
当动点M满足,但时,与平面相交.
40.(1)证明见解析;
(2)证明见解析.
【解析】
【分析】
(1)证明即可证明结论
(2)根据线面平行的判定定理证明即可.
(1)
证明:因为E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,
所以,
所以,
所以四点E,F,G,H共面.
(2)
证明:因为E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,
所以,
因为平面,平面,平面,平面,
所以平面, 平面
41.(1)证明见解析;(2).
【解析】
【分析】
(1)连接A1B交AB1于点O,连接OD1,可得OD1∥BC1,由线面平行的判定定理即可证明BC1∥平面AB1D1;
(2)由V1====V2,即可求得结论.
【详解】
(1)证明:连接A1B交AB1于点O,连接OD1,
则在平形四边形ABB1A1中,点O为A1B的中点,
又点D1为A1C1的中点,
所以OD1∥BC1,
又OD1 平面AB1D1,B1C 平面AB1D1,
所以BC1∥平面AB1D1.
(2)V1====V2
所以=.
试卷第1页,共3页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
